CRC(Cyclic Redundancy Check),即循环冗余校验,它通过计算生成固定长度的校验码,用于验证数据在传输过程中是否发生了错误或损坏,从而确保数据的完整性。假设我们想把小写字母z发送出去。在Unicode中,z由数字0x7A表示,二进制为0111 1010。为了使接收方能够验证数据在传输时有没有被修改,我们计算出该数据的CRC为1000,并附加到我们的消息之后:0111 1010 1000。这个校验值1000被称为冗余,因为它是在原来数据的基础上增加的。
文章目录
- 1 CRC计算
- 1.1 多项式
- 1.2 模二除法计算及例子
- 1.3 CRC类型
- 2 多项式的选择
- 3 总结
1 CRC计算
1.1 多项式
从数学上讲,CRC是数据的模二多项式(polynomial)除法的余数。因此,CRC可以写成
CRC = data % 2 polynomial
该多项式可以是任何数学多项式(没有任何系数),但是它的最高指数不能超过CRC的位数。比如我们要生成一个8位CRC,那么多项式的最高指数也必须是8,比如:
x
8
+
x
2
+
x
+
1
x^8+x^2+x+1
x8+x2+x+1。而多项式都可以转换成二进制来表示,实际上就是看从每个指数是否存在,存在则为1,不存在则为0。比如说
x
8
+
x
2
+
x
+
1
x^8+x^2+x+1
x8+x2+x+1转换成二进制为100000111。
- 选择不同的多项式将导致相同数据产生不同的CRC。所以发送方和接收方需要使用共同的多项式
- 对于CRC来说,根据具体的使用场景,有些多项式比其他多项式更适合使用。例如,某些多项式可能更容易检测出连续位错误或交替位错误。
接下来,为了能够计算CRC,我们需要了解模二除法。
1.2 模二除法计算及例子
(1)模二运算
模二运算是对二进制数逐位进行的运算。在这种运算中,不存在进位或借位,每个位被视为独立于其相邻位的数字。实际上就是C语言中的异或运算:
| bit1 | bit2 | XOR |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
(2)模二除法
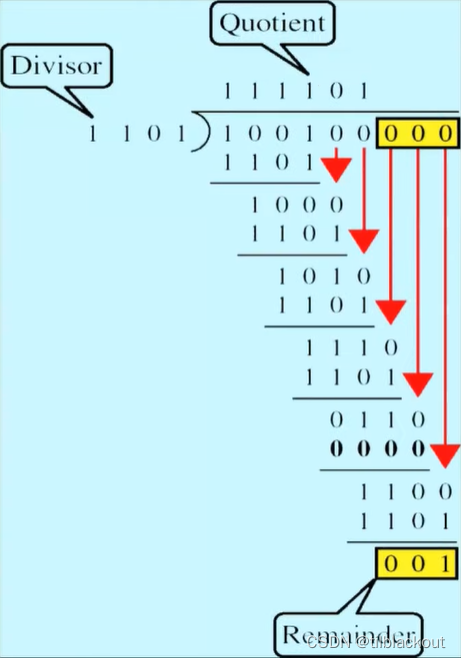
模二除法的执行类似于算术除法,唯一的区别是我们使用模二减法(XOR)而不是算术减法来计算每一步的余数。假设被除数为111101,除数为1101,下面来看一下如何计算出CRC:
- 计算除数的长度为为
L,这里为4。 - 在被除数的后面加上
L-1位,这里为3,这也是CRC的长度。注意:除数的最高位必须为1,附加的位数就对应二项式中的最高指数: x 3 + x 2 + 1 x^3+x^2+1 x3+x2+1 - 用二进制模二进行计算,得到的余数即CRC的结果:
001
1.3 CRC类型
CRC类型由其位大小命名。常见的有:CRC-8、CRC-16、CRC-32、CRC-64和CRC-1(奇偶校验位的特例)。显然对于同一个类型,不同的多项式也有不同的结果。比如对于被除数01000001来说,它的CRC-8在不同的多项式下的结果如下:
| 二进制多项式 | CRC-8 |
|---|---|
| 110100111 | 11001100 |
| 100000111 | 11000000 |
| 101001001 | 01100110 |
| 111010101 | 01001000 |
- 以上是在蓝牙、
GSM-B等不同应用中使用的标准CRC-8多项式
2 多项式的选择
我们应该如何选择合适的CRC和相应的多项式?有三个方面需要考虑:随机错误检测精度、突发错误检测精度和冗余系数。
(1)随机错误检测精度
随机错误是指在数据中随机出现的错误。例如,在传输数据时,单个比特被翻转,或者在传输过程中丢失几个比特。根据我们使用的CRC的位大小,我们可以检测到大多数这些随机错误。然而,对于CRC-n来说,这些错误的
1
/
2
n
1/2^n
1/2n不能被检测到。下表显示了每种CRC类型未检测到错误的百分比:
| CRC | 不可检测错误 | 百分比% |
|---|---|---|
| CRC-8 | 1 / 2 8 1/2^8 1/28 | 0.39 |
| CRC-16 | 1 / 2 16 1/2^{16} 1/216 | 0.0015 |
| CRC-32 | 1 / 2 32 1/2^{32} 1/232 | 0.00000002 |
| CRC-64 | 1 / 2 64 1/2^{64} 1/264 | 5.4 × 1 0 − 20 5.4×10^{-20} 5.4×10−20 |
(2)突发错误检测精度
数据传输中的错误通常不是随机的,而是连续的出现几个位的错误,这种错误称为突发错误,它是数据通信中最常见的错误。
CRC-n可以检测最大长度为n位的单突发错误。然而,这在很大程度上取决于用于计算CRC的多项式。有些多项式能够检测到传输数据中的多个突发错误。
| CRC | 突发差错检测 |
|---|---|
| CRC-8 | 至少出现一个连续的错误突发,但这个长度≤8位 |
| CRC-16 | 至少出现一个连续的错误突发,但这个长度≤16位 |
| CRC-32 | 至少出现一个连续的错误突发,但这个长度≤32位 |
| CRC-64 | 至少出现一个连续的错误突发,但这个长度≤64位 |
(3)冗余系数
使用CRC进行错误检测的代价是要增加额外的数据。比如CRC-32要比CRC-16多传输两个额外的字节。显然,比特位数较低的CRC只需要计算和存储更少的位数。
基于这三个因素,我们可以决定选择哪种CRC类型用于我们的应用程序。然而,CRC多项式也会影响错误检测的效率和质量。如果要深入研究的话,将是一个很复杂的话题,本文不做研究。幸运的是,网上有很多种用于特定CRC类型的标准多项式,在大多数情况下,使用其中之一就能有不错的检错效果。
3 总结
CRC校验在做项目的过程中经常会使用到,在我上大学的时候有浅浅地理解这个计算的过程,后面工作了就是直接用NXP SDK中写的软件CRC的代码。说实话,我看不懂这简简单单的几行CRC-32查表算法,但我不希望我只是会用这些函数,而是要理解其中的原理。所以我开始写这一系列的博客深入地研究和理解常见的一些算法,希望能有所收获。
对于现在的CPU来说,大多都在硬件上实现了CRC校验,但我想从软件上来实现CRC32的查表算法,包括表格的生成和CRC的计算。另外,CRC一般有两种:反射CRC和非反射CRC,这两种方式在实际应用中并没有明显的性能或准确性差异,选择哪种方式主要取决于应用的需求和标准。但这些也都需要考虑到,在后面的文章中我都将一一详细地讲解并实现…