引言
这是统计学习方法第十一章条件随机场的阅读笔记,包含所有公式的详细推导。
条件随机场(conditional random field,CRF)是给定一组输入随机变量条件下另一组输出随机变量的条件概率分布模型,其特点是假设输出随机变量构成马尔可夫随机场。
建议先阅读概率图简介,了解一些概率图的知识。
- 《统计学习方法》——条件随机场(上)
- 《统计学习方法》——条件随机场(中)
- 《统计学习方法》——条件随机场(下)
- 《统计学习方法》——条件随机场#习题解答#
条件随机场的概率计算问题
前向-后向算法
概率计算问题不可避免的涉及到计算
Z
(
x
)
Z(x)
Z(x),我们知道
Z
(
x
)
=
∑
y
∏
i
=
1
n
+
1
M
i
(
y
i
−
1
,
y
i
∣
x
)
Z(x) = \sum_y \prod_{i=1}^{n+1} M_i(y_{i-1},y_i|x)
Z(x)=y∑i=1∏n+1Mi(yi−1,yi∣x)
是以start为起点stop为终点通过状态的所有路径
y
1
y
2
⋯
y
n
y_1y_2\cdots y_n
y1y2⋯yn的非规范化概率之
∏
i
=
1
n
+
1
M
i
(
y
i
−
1
,
y
i
∣
x
)
\prod_{i=1}^{n+1} M_i(y_{i-1},y_i|x)
∏i=1n+1Mi(yi−1,yi∣x)之和。
即它可以写成:
Z
(
x
)
=
∑
y
1
⋯
∑
y
i
−
1
∑
y
i
+
1
⋯
∑
y
n
∏
i
=
1
n
+
1
M
i
(
y
i
−
1
,
y
i
∣
x
)
(p1)
Z(x) = \sum_{y_1} \cdots \sum_{y_{i-1}} \sum_{y_{i+1}} \cdots \sum_{y_n} \prod_{i=1}^{n+1} M_i(y_{i-1},y_i|x) \tag{p1}
Z(x)=y1∑⋯yi−1∑yi+1∑⋯yn∑i=1∏n+1Mi(yi−1,yi∣x)(p1)
从左往右看,这里有
n
n
n个求和,此时复杂度为
O
(
n
)
O(n)
O(n),而每个求和中
y
i
y_i
yi的取值有
m
m
m个,所以复杂度变成了
O
(
m
n
)
O(m^n)
O(mn),而最后还有
n
+
1
n+1
n+1个连乘,最终复杂度为
O
(
m
n
⋅
n
)
O(m^n \cdot n)
O(mn⋅n)。这在计算上是不可行的。
类似HMM,这里也基于动态规划引入前向和后向算法,使得时间复杂度降低成 O ( n ⋅ m 2 ) O(n \cdot m^2) O(n⋅m2)。
我们把上式
(
p
1
)
(p1)
(p1)展开,并且为了统一,多加了一个
∑
y
0
\sum_{y_0}
∑y0,我们上面引入
y
0
=
start
y_0=\text{start}
y0=start,只有一个取值,我们也可以把它看成一个向量,非
start
\text{start}
start位置取值为
0
0
0,只有
start
\text{start}
start位置取值为
1
1
1:
Z
(
x
)
=
∑
y
0
∑
y
1
⋯
∑
y
i
−
1
∑
y
i
+
1
⋯
∑
y
n
∏
i
=
1
n
+
1
M
i
(
y
i
−
1
,
y
i
∣
x
)
=
∑
y
0
∑
y
1
⋯
∑
y
i
−
1
∑
y
i
+
1
⋯
∑
y
n
M
1
(
y
0
,
y
1
∣
x
)
M
2
(
y
1
,
y
2
∣
x
)
⋯
M
i
(
y
i
−
1
,
y
i
∣
x
)
M
i
+
1
(
y
i
,
y
i
+
1
∣
x
)
⋯
M
n
+
1
(
y
n
,
y
n
+
1
∣
x
)
\begin{aligned} Z(x) &= \sum_{y_0}\sum_{y_1} \cdots \sum_{y_{i-1}} \sum_{y_{i+1}} \cdots \sum_{y_n} \prod_{i=1}^{n+1} M_i(y_{i-1},y_i|x) \\ &= \sum_{y_0}\sum_{y_1} \cdots \sum_{y_{i-1}} \sum_{y_{i+1}} \cdots \sum_{y_n} M_1(y_0,y_1|x) M_2(y_1,y_2|x)\cdots M_i(y_{i-1},y_i|x) M_{i+1}(y_{i},y_{i+1}|x) \cdots M_{n+1}(y_n,y_{n+1}|x) \end{aligned}
Z(x)=y0∑y1∑⋯yi−1∑yi+1∑⋯yn∑i=1∏n+1Mi(yi−1,yi∣x)=y0∑y1∑⋯yi−1∑yi+1∑⋯yn∑M1(y0,y1∣x)M2(y1,y2∣x)⋯Mi(yi−1,yi∣x)Mi+1(yi,yi+1∣x)⋯Mn+1(yn,yn+1∣x)
观察上式,每个因子
M
j
(
y
j
−
1
,
y
j
∣
x
)
M_j(y_{j-1},y_j|x)
Mj(yj−1,yj∣x)只与两个变量
y
j
−
1
y_{j-1}
yj−1和
y
j
y_j
yj有关,因此,可以重写一下上式:
Z
(
x
)
=
∑
y
n
M
n
+
1
(
y
n
,
y
n
+
1
∣
x
)
⋯
∑
y
i
+
1
M
i
+
2
(
y
i
+
1
,
y
i
+
2
∣
x
)
∑
y
i
M
i
+
1
(
y
i
,
y
i
+
1
∣
x
)
∑
y
i
−
1
M
i
(
y
i
−
1
,
y
i
∣
x
)
⋯
∑
y
2
M
3
(
y
2
,
y
3
∣
x
)
∑
y
1
M
2
(
y
1
,
y
2
∣
x
)
∑
y
0
M
1
(
y
0
,
y
1
∣
x
)
(p2)
Z(x) = \sum_{y_n} M_{n+1}(y_n,y_{n+1}|x) \cdots \sum_{y_{i+1}} M_{i+2}(y_{i+1},y_{i+2}|x)\sum_{y_i} M_{i+1}(y_{i},y_{i+1}|x) \sum_{y_{i-1}} M_i(y_{i-1},y_i|x) \\ \cdots \sum_{y_2} M_3(y_2,y_3|x) \sum_{y_1} M_2(y_1,y_2|x)\sum_{y_0} M_1(y_0,y_1|x) \tag{p2}
Z(x)=yn∑Mn+1(yn,yn+1∣x)⋯yi+1∑Mi+2(yi+1,yi+2∣x)yi∑Mi+1(yi,yi+1∣x)yi−1∑Mi(yi−1,yi∣x)⋯y2∑M3(y2,y3∣x)y1∑M2(y1,y2∣x)y0∑M1(y0,y1∣x)(p2)
类似上面的例题,我们也画出这个
Z
(
x
)
Z(x)
Z(x)的状态路径图(假设start和stop都在第一个状态位置):
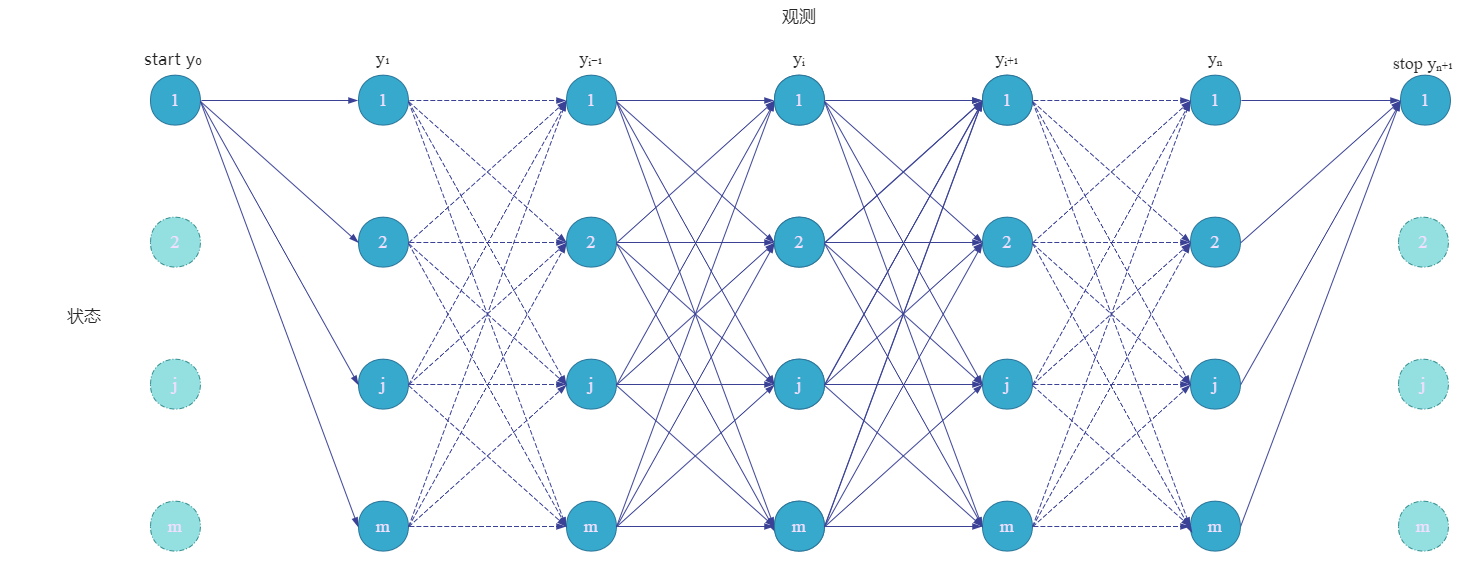
我们针对 ( p 2 ) (p2) (p2)式从右往左看,看如何对应上图中的结点位置。首先最右边的 ∑ y 0 M 1 ( y 0 , y 1 ∣ x ) \sum_{y_0} M_1(y_0,y_1|x) ∑y0M1(y0,y1∣x)
我们知道 M 1 ( y 0 , y 1 ∣ x ) = exp ( ∑ k = 1 K w k f k ( y 0 , y 1 , x , 1 ) ) M_1(y_0,y_1|x)= \exp(\sum_{k=1}^K w_kf_k(y_0,y_1,x,1)) M1(y0,y1∣x)=exp(∑k=1Kwkfk(y0,y1,x,1))表示从 y 0 y_0 y0到 y 1 y_1 y1的非规范化概率。
基于上面的一个向量的情况下,那么
∑
y
0
M
1
(
y
0
,
y
1
∣
x
)
=
M
1
(
y
0
=
1
,
y
1
∣
x
)
+
M
1
(
y
0
=
2
,
y
1
∣
x
)
+
⋯
+
M
1
(
y
0
=
m
,
y
1
∣
x
)
(p3)
\sum_{y_0} M_1(y_0,y_1|x)=M_1(y_0=1,y_1|x)+M_1(y_0=2,y_1|x)+\cdots + M_1(y_0=m,y_1|x) \tag{p3}
y0∑M1(y0,y1∣x)=M1(y0=1,y1∣x)+M1(y0=2,y1∣x)+⋯+M1(y0=m,y1∣x)(p3)
这里先假设
y
1
y_1
y1取固定值,假设是
1
1
1,那么
(
p
3
)
(p3)
(p3)做的事情就是如下图:
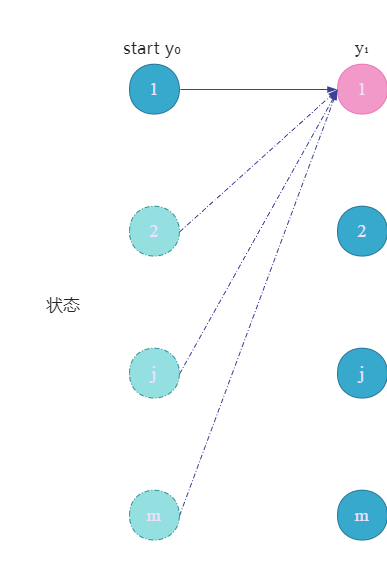
我们看出来了,就是计算所有的前一个状态 y 0 y_0 y0到 y 1 y_1 y1的非规范化概率,得到的是一个标量。
我们知道,实际上只有start位置到 y 1 y_1 y1的那条连线才有意义,假设 y 0 = 1 = start y_0=1=\text{start} y0=1=start,那么实际上计算的是 M 1 ( y 0 = 1 , y 1 ∣ x ) M_1(y_0=1,y_1|x) M1(y0=1,y1∣x)。所有 y 0 y_0 y0对应竖排非start的结点和连线都是虚线,画出来是为了和后面步骤统一。
上面是固定
y
1
=
1
y_1=1
y1=1,即状态1的情况,实际
(
p
2
)
(p2)
(p2)中的
∑
y
0
\sum_{y_0}
∑y0前面还有一个
∑
y
1
\sum_{y_1}
∑y1:$\sum_{y_1} M_2(y_1,y_2|x)\sum_{y_0} M_1(y_0,y_1|x) $。这是一种简写形式,完整的写法应该是:
∑
y
1
M
2
(
y
1
,
y
2
∣
x
)
∑
y
0
M
1
(
y
0
,
y
1
∣
x
)
=
∑
y
1
(
M
2
(
y
1
,
y
2
∣
x
)
∑
y
0
M
1
(
y
0
,
y
1
∣
x
)
)
\sum_{y_1} M_2(y_1,y_2|x)\sum_{y_0} M_1(y_0,y_1|x) = \sum_{y_1} \left(M_2(y_1,y_2|x)\sum_{y_0} M_1(y_0,y_1|x) \right)
y1∑M2(y1,y2∣x)y0∑M1(y0,y1∣x)=y1∑(M2(y1,y2∣x)y0∑M1(y0,y1∣x))
暂时忽略
M
2
(
y
1
,
y
2
∣
x
)
M_2(y_1,y_2|x)
M2(y1,y2∣x)的情况下,显然要计算所有的
y
1
y_1
y1。即实际上
y
1
y_1
y1也可以有
m
m
m种取值,所以
(
p
3
)
(p3)
(p3)实际上计算出的是一个
m
m
m维的向量——从所有的
y
0
y_0
y0到所有的
y
1
y_1
y1的非规范化概率。
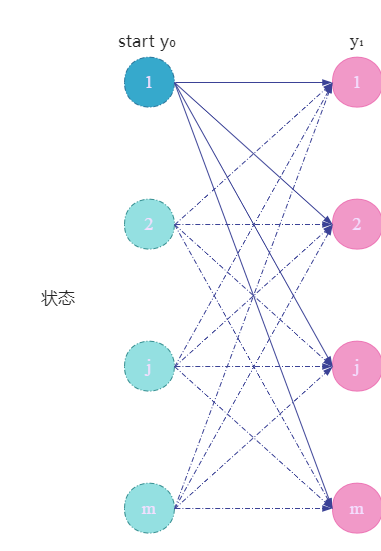
就如上图所示。
如果考虑所有
y
1
y_1
y1的情况下,那么
∑
y
0
M
1
(
y
0
,
y
1
∣
x
)
\sum_{y_0} M_1(y_0,y_1|x)
∑y0M1(y0,y1∣x)的计算可以用一个向量和矩阵相乘表示:
∑
y
0
M
1
(
y
0
,
y
1
∣
x
)
=
v
1
×
m
⋅
[
M
1
(
y
0
,
y
1
∣
x
)
]
m
×
m
(p4)
\begin{aligned} \sum_{y_0} M_1(y_0,y_1|x) &= \pmb v_{1\times m} \cdot [M_1(y_0,y_1|x)]_{m\times m} \end{aligned} \tag{p4}
y0∑M1(y0,y1∣x)=v1×m⋅[M1(y0,y1∣x)]m×m(p4)
这向量
v
\pmb v
v就是我们上面说的
y
0
y_0
y0对应的竖排向量,类似HMM中前向后向算法的表示,我们也用
α
0
(
y
∣
x
)
\alpha_0(y|x)
α0(y∣x)表示这个包含
y
0
y_0
y0初始状态的向量:
α
0
(
y
∣
x
)
=
{
1
,
y
=
start
0
,
else
(11.26)
\alpha_0(y|x) = \begin{cases} 1, & y=\text{start} \\ 0 , & \text{else} \end{cases} \tag{11.26}
α0(y∣x)={1,0,y=startelse(11.26)
那么(值为1表示start位置)
α
0
(
x
)
=
[
α
0
(
y
0
=
1
∣
x
)
⋮
α
0
(
y
0
=
j
∣
x
)
⋮
α
0
(
y
0
=
m
∣
x
)
]
m
=
[
1
⋮
0
⋮
0
]
m
\alpha_0(x) = \begin{bmatrix} \alpha_0(y_0=1|x)\\ \vdots\\ \alpha_0(y_0=j|x) \\ \vdots\\ \alpha_0(y_0=m|x) \end{bmatrix}_m =\begin{bmatrix} 1\\ \vdots\\ 0 \\ \vdots\\ 0 \end{bmatrix}_m
α0(x)=
α0(y0=1∣x)⋮α0(y0=j∣x)⋮α0(y0=m∣x)
m=
1⋮0⋮0
m
这是一个
m
×
1
m \times 1
m×1的列向量,
(
p
4
)
(p4)
(p4)中的是一个行向量,我们变成行向量加个转置
α
0
T
(
x
)
\alpha_0^T(x)
α0T(x)。
那么
(
p
4
)
(p4)
(p4)用新的向量表示为:
∑
y
0
M
1
(
y
0
,
y
1
∣
x
)
=
v
1
×
m
⋅
[
M
1
(
y
0
,
y
1
∣
x
)
]
m
×
m
=
α
0
T
(
x
)
1
×
m
⋅
[
M
1
(
y
0
,
y
1
∣
x
)
]
m
×
m
=
α
0
T
(
x
)
1
×
m
⋅
M
1
(
x
)
m
×
m
\begin{aligned} \sum_{y_0} M_1(y_0,y_1|x) &= \pmb v_{1\times m} \cdot [M_1(y_0,y_1|x)]_{m\times m} \\ &= \alpha_0^T(x)_{1 \times m} \cdot [M_1(y_0,y_1|x)]_{m\times m} \\ &= \alpha_0^T(x)_{1 \times m} \cdot M_1(x)_{m\times m} \end{aligned}
y0∑M1(y0,y1∣x)=v1×m⋅[M1(y0,y1∣x)]m×m=α0T(x)1×m⋅[M1(y0,y1∣x)]m×m=α0T(x)1×m⋅M1(x)m×m
公式
(
p
3
)
(p3)
(p3)计算出的新的向量,用
α
1
(
x
)
\alpha_1(x)
α1(x)表示,即
α
1
T
(
x
)
=
α
0
T
(
x
)
⋅
M
1
(
x
)
\alpha_1^T(x) =\alpha_0^T(x) \cdot M_1(x)
α1T(x)=α0T(x)⋅M1(x)
基于这个新向量,可以改写
(
p
2
)
(p2)
(p2)为:
Z
(
x
)
=
∑
y
n
M
n
+
1
(
y
n
,
y
n
+
1
∣
x
)
⋯
∑
y
i
+
1
M
i
+
2
(
y
i
+
1
,
y
i
+
2
∣
x
)
∑
y
i
M
i
+
1
(
y
i
,
y
i
+
1
∣
x
)
∑
y
i
−
1
M
i
(
y
i
−
1
,
y
i
∣
x
)
⋯
∑
y
2
M
3
(
y
2
,
y
3
∣
x
)
∑
y
1
M
2
(
y
1
,
y
2
∣
x
)
∑
y
0
M
1
(
y
0
,
y
1
∣
x
)
=
∑
y
n
M
n
+
1
(
y
n
,
y
n
+
1
∣
x
)
⋯
∑
y
i
+
1
M
i
+
2
(
y
i
+
1
,
y
i
+
2
∣
x
)
∑
y
i
M
i
+
1
(
y
i
,
y
i
+
1
∣
x
)
∑
y
i
−
1
M
i
(
y
i
−
1
,
y
i
∣
x
)
⋯
∑
y
2
M
3
(
y
2
,
y
3
∣
x
)
∑
y
1
α
1
(
y
1
∣
x
)
M
2
(
y
1
,
y
2
∣
x
)
(p5)
\begin{aligned} Z(x) &= \sum_{y_n} M_{n+1}(y_n,y_{n+1}|x) \cdots \sum_{y_{i+1}} M_{i+2}(y_{i+1},y_{i+2}|x)\sum_{y_i}M_{i+1}(y_{i},y_{i+1}|x) \sum_{y_{i-1}} M_i(y_{i-1},y_i|x) \cdots \sum_{y_2} M_3(y_2,y_3|x) \sum_{y_1} M_2(y_1,y_2|x)\sum_{y_0} M_1(y_0,y_1|x)\\ &= \sum_{y_n} M_{n+1}(y_n,y_{n+1}|x) \cdots \sum_{y_{i+1}} M_{i+2}(y_{i+1},y_{i+2}|x)\sum_{y_i} M_{i+1}(y_{i},y_{i+1}|x) \sum_{y_{i-1}} M_i(y_{i-1},y_i|x) \cdots \sum_{y_2} M_3(y_2,y_3|x) \sum_{y_1} \alpha_1(y_1|x) M_2(y_1,y_2|x) \end{aligned} \tag{p5}
Z(x)=yn∑Mn+1(yn,yn+1∣x)⋯yi+1∑Mi+2(yi+1,yi+2∣x)yi∑Mi+1(yi,yi+1∣x)yi−1∑Mi(yi−1,yi∣x)⋯y2∑M3(y2,y3∣x)y1∑M2(y1,y2∣x)y0∑M1(y0,y1∣x)=yn∑Mn+1(yn,yn+1∣x)⋯yi+1∑Mi+2(yi+1,yi+2∣x)yi∑Mi+1(yi,yi+1∣x)yi−1∑Mi(yi−1,yi∣x)⋯y2∑M3(y2,y3∣x)y1∑α1(y1∣x)M2(y1,y2∣x)(p5)
即在固定
y
2
y_2
y2的情况下,计算从
y
0
y_0
y0到
y
2
y_2
y2的所有非规范化概率:
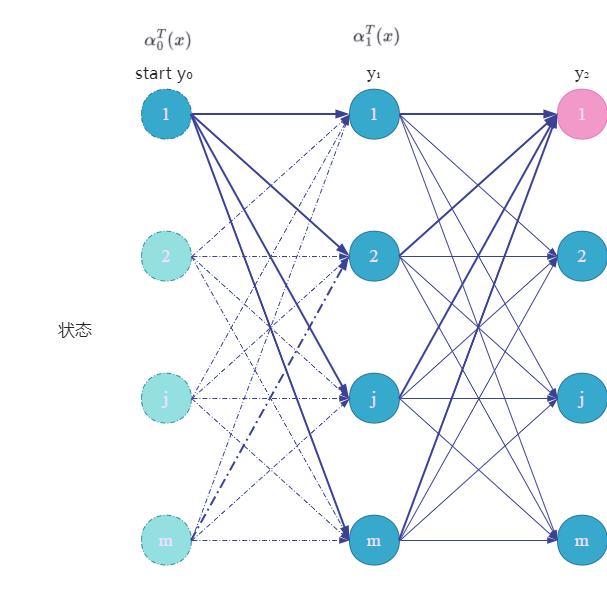
上图是假设 y 2 = 1 y_2=1 y2=1时的情形,用加粗的箭头表示实际进行了的计算。同理我们知道,实际上会计算所有可能的 y 2 y_2 y2,即计算出 α 2 T ( x ) \alpha_2^T(x) α2T(x)。
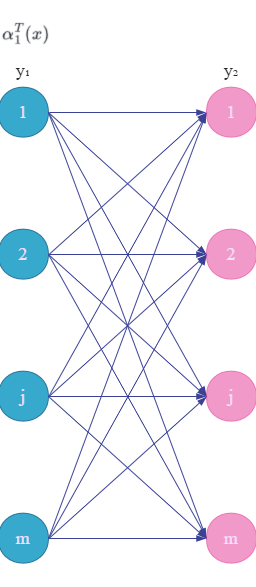
如上图红色结点所示,表示计算从 y 0 y_0 y0到 y 2 y_2 y2的所有非规范化概率。那么对于每个指标 i = 0 , 1 , ⋯ , n + 1 i=0,1,\cdots,n+1 i=0,1,⋯,n+1,定义一个前向向量 α i ( x ) \alpha_i(x) αi(x):
α
i
(
x
)
=
[
α
i
(
y
i
=
1
∣
x
)
α
i
(
y
i
=
2
∣
x
)
⋮
α
i
(
y
i
=
i
∣
x
)
⋮
α
i
(
y
i
=
m
∣
x
)
]
m
\alpha_i(x)=\begin{bmatrix} \alpha_i(y_i=1|x)\\ \alpha_i(y_i=2|x)\\ \vdots\\ \alpha_i(y_i=i|x)\\ \vdots\\ \alpha_i(y_i=m|x) \end{bmatrix}_m
αi(x)=
αi(yi=1∣x)αi(yi=2∣x)⋮αi(yi=i∣x)⋮αi(yi=m∣x)
m
α
i
(
y
i
∣
x
)
\alpha_i(y_i|x)
αi(yi∣x)表示在位置
i
i
i的标记是
y
i
y_i
yi且从
1
1
1到
i
i
i(
y
0
y_0
y0到
y
i
y_i
yi)的前部分标记序列的非规范化概率。
α
i
(
y
i
∣
x
)
=
α
i
−
1
T
(
y
i
−
1
∣
x
)
[
M
i
(
y
i
−
1
,
y
i
∣
x
)
]
,
i
=
1
,
2
,
⋯
,
n
+
1
(11.27)
\alpha_i(y_i|x) = \alpha_{i-1}^T(y_{i-1}|x)[M_i(y_{i-1},y_i|x)],\quad i=1,2,\cdots, n+1 \tag{11.27}
αi(yi∣x)=αi−1T(yi−1∣x)[Mi(yi−1,yi∣x)],i=1,2,⋯,n+1(11.27)
又可以表示为:
α
i
T
(
x
)
=
α
i
−
1
T
(
x
)
M
i
(
x
)
(11.28)
\alpha_i^T(x)= \alpha_{i-1}^T(x)M_i(x) \tag{11.28}
αiT(x)=αi−1T(x)Mi(x)(11.28)
此时从 y 1 y_1 y1到 y 2 y_2 y2的过程中,我们可以看到,在 y 1 y_1 y1需要计算 m m m个结点,即 α 1 ( x ) \alpha_1(x) α1(x)向量中的每个元素,在 y 2 y_2 y2也需要根据 y 1 y_1 y1计算 m m m个结点。这个过程需要计算 m × m m \times m m×m次。如果序列长度为 n + 1 n+1 n+1,那么共有 n n n个这样的操作,显然整个过程的时间复杂度为 O ( m 2 ⋅ n ) O(m^2\cdot n) O(m2⋅n)。
假设我们基于此过程已经计算出了
α
n
T
(
x
)
\alpha_n^T(x)
αnT(x),我们来看最后一步是怎么样的。此时,对应的
(
p
5
)
(p5)
(p5)变成了:
Z
(
x
)
=
∑
y
n
α
n
(
y
n
∣
x
)
M
n
+
1
(
y
n
,
y
n
+
1
∣
x
)
=
∑
y
n
α
n
(
y
n
∣
x
)
M
n
+
1
(
y
n
,
y
n
+
1
=
stop
∣
x
)
Z(x) = \sum_{y_n} \alpha_n(y_n|x) M_{n+1}(y_n,y_{n+1}|x) = \sum_{y_n} \alpha_n(y_n|x) M_{n+1}(y_n,y_{n+1}=\text{stop}|x)
Z(x)=yn∑αn(yn∣x)Mn+1(yn,yn+1∣x)=yn∑αn(yn∣x)Mn+1(yn,yn+1=stop∣x)
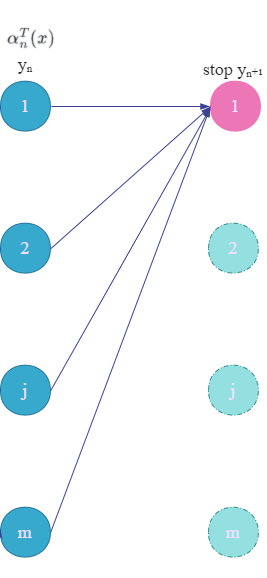
因为
stop
\text{stop}
stop也只有一个,按照我们前面的理解,最终得到的是汇聚到
y
n
+
1
=
stop
y_{n+1}=\text{stop}
yn+1=stop结点上的标量。即
Z
(
x
)
=
∑
y
n
α
n
(
y
n
∣
x
)
M
n
+
1
(
y
n
,
y
n
+
1
∣
x
)
=
∑
y
n
α
n
(
y
n
∣
x
)
M
n
+
1
(
y
n
,
y
n
+
1
=
stop
∣
x
)
=
α
n
(
y
n
=
1
∣
x
)
M
n
+
1
(
y
n
=
1
,
y
n
+
1
=
stop
∣
x
)
+
α
n
(
y
n
=
2
∣
x
)
M
n
+
1
(
y
n
=
2
,
y
n
+
1
=
stop
∣
x
)
+
⋯
+
α
n
(
y
n
=
m
∣
x
)
M
n
+
1
(
y
n
=
m
,
y
n
+
1
=
stop
∣
x
)
\begin{aligned} Z(x) &= \sum_{y_n} \alpha_n(y_n|x) M_{n+1}(y_n,y_{n+1}|x)\\ &= \sum_{y_n} \alpha_n(y_n|x) M_{n+1}(y_n,y_{n+1}=\text{stop}|x) \\ &= \alpha_n(y_n=1|x) M_{n+1}(y_n=1,y_{n+1}=\text{stop}|x) + \alpha_n(y_n=2|x) M_{n+1}(y_n=2,y_{n+1}=\text{stop}|x) + \cdots + \alpha_n(y_n=m|x) M_{n+1}(y_n=m,y_{n+1}=\text{stop}|x) \end{aligned}
Z(x)=yn∑αn(yn∣x)Mn+1(yn,yn+1∣x)=yn∑αn(yn∣x)Mn+1(yn,yn+1=stop∣x)=αn(yn=1∣x)Mn+1(yn=1,yn+1=stop∣x)+αn(yn=2∣x)Mn+1(yn=2,yn+1=stop∣x)+⋯+αn(yn=m∣x)Mn+1(yn=m,yn+1=stop∣x)
对应上面的这些连线,如果把上式后面的结果写成向量化形式的话:
Z
(
x
)
=
α
n
T
(
x
)
1
×
m
⋅
1
m
×
1
Z(x) = \alpha_n^T(x)_{1 \times m} \cdot \pmb{1}_{m \times 1}
Z(x)=αnT(x)1×m⋅1m×1
上面我们讨论的是前向算法,那么对于后向算法也是同样的思想。
类似 ( p 2 ) (p2) (p2),我们按另一个顺序,从后往前。
首先对于每个指标
i
=
0
,
1
,
⋯
,
n
+
1
i=0,1,\cdots,n+1
i=0,1,⋯,n+1,定义后向向量
β
i
(
x
)
\beta_i(x)
βi(x):
β
n
+
1
(
y
n
+
1
∣
x
)
=
{
1
,
y
n
+
1
=
stop
0
,
else
(11.29)
\beta_{n+1}(y_{n+1}|x) = \begin{cases} 1, & y_{n+1}=\text{stop} \\ 0 , & \text{else} \end{cases} \tag{11.29}
βn+1(yn+1∣x)={1,0,yn+1=stopelse(11.29)
β n + 1 ( x ) \beta_{n+1}(x) βn+1(x)是一个 m × 1 m \times 1 m×1的列向量,只有一个元素为 1 1 1,其他元素为 0 0 0。
Z ( x ) = ∑ y 1 ⋯ ∑ y i − 1 ∑ y i + 1 ⋯ ∑ y n ∏ i = 1 n + 1 M i ( y i − 1 , y i ∣ x ) = ∑ y 1 ⋯ ∑ y i − 1 ∑ y i + 1 ⋯ ∑ y n ∑ y n + 1 M 1 ( y 0 , y 1 ∣ x ) M 2 ( y 1 , y 2 ∣ x ) ⋯ M i ( y i − 1 , y i ∣ x ) M i + 1 ( y i , y i + 1 ∣ x ) ⋯ M n + 1 ( y n , y n + 1 ∣ x ) = ∑ y 1 M 1 ( y 0 , y 1 ∣ x ) ⋯ ∑ y n M n ( y n − 1 , y n ∣ x ) ∑ y n + 1 M n + 1 ( y n , y n + 1 ∣ x ) (p6) \begin{aligned} Z(x) &= \sum_{y_1} \cdots \sum_{y_{i-1}} \sum_{y_{i+1}} \cdots \sum_{y_n} \prod_{i=1}^{n+1} M_i(y_{i-1},y_i|x) \\ &= \sum_{y_1} \cdots \sum_{y_{i-1}} \sum_{y_{i+1}} \cdots \sum_{y_n}\sum_{y_{n+1}} M_1(y_0,y_1|x) M_2(y_1,y_2|x)\cdots M_i(y_{i-1},y_i|x) M_{i+1}(y_{i},y_{i+1}|x) \cdots M_{n+1}(y_n,y_{n+1}|x) \\ &= \sum_{y_1} M_1(y_0,y_1|x) \cdots \sum_{y_n} M_{n}(y_{n-1},y_{n}|x) \sum_{y_{n+1}} M_{n+1}(y_n,y_{n+1}|x) \end{aligned} \tag{p6} Z(x)=y1∑⋯yi−1∑yi+1∑⋯yn∑i=1∏n+1Mi(yi−1,yi∣x)=y1∑⋯yi−1∑yi+1∑⋯yn∑yn+1∑M1(y0,y1∣x)M2(y1,y2∣x)⋯Mi(yi−1,yi∣x)Mi+1(yi,yi+1∣x)⋯Mn+1(yn,yn+1∣x)=y1∑M1(y0,y1∣x)⋯yn∑Mn(yn−1,yn∣x)yn+1∑Mn+1(yn,yn+1∣x)(p6)
从后往前的状态路径图如下图所示:

同样先根据
(
p
6
)
(p6)
(p6)最后一个求和有:
β
n
(
y
n
∣
x
)
=
∑
y
n
+
1
M
n
+
1
(
y
n
,
y
n
+
1
∣
x
)
=
[
M
n
+
1
(
y
n
,
y
n
+
1
∣
x
)
]
m
×
m
⋅
β
n
+
1
(
y
n
+
1
∣
x
)
m
×
1
\begin{aligned} \beta_{n}(y_{n}|x) = \sum_{y_{n+1}} M_{n+1}(y_n,y_{n+1}|x) &= [M_{n+1}(y_n,y_{n+1}|x)]_{m\times m} \cdot \beta_{n+1}(y_{n+1}|x)_{m \times 1} \end{aligned}
βn(yn∣x)=yn+1∑Mn+1(yn,yn+1∣x)=[Mn+1(yn,yn+1∣x)]m×m⋅βn+1(yn+1∣x)m×1
同理,我们可以得到
β
i
(
y
i
∣
x
)
=
[
M
i
+
1
(
y
i
,
y
i
+
1
∣
x
)
]
β
i
+
1
(
y
i
+
1
∣
x
)
(11.30)
\beta_i(y_i|x) = [M_{i+1}(y_i,y_{i+1}|x)]\beta_{i+1}(y_{i+1}|x) \tag{11.30}
βi(yi∣x)=[Mi+1(yi,yi+1∣x)]βi+1(yi+1∣x)(11.30)
可以表示为
β
i
(
x
)
=
M
i
+
1
β
i
+
1
(
x
)
(11.31)
\beta_i(x) = M_{i+1}\beta_{i+1}(x) \tag{11.31}
βi(x)=Mi+1βi+1(x)(11.31)
β i ( y i ∣ x ) \beta_i(y_i|x) βi(yi∣x)表示未知 i i i的标记为 y i y_i yi并且从 i + 1 i+1 i+1到 n n n的后部分标记序列的非规范化概率。
注意 α i ( y i ∣ x ) \alpha_i(y_i|x) αi(yi∣x)和 β i ( y i ∣ x ) \beta_i(y_i|x) βi(yi∣x)都是累计向量,前者表示从 1 1 1到 i i i的前部分标记序列的非规范化概率。
我们来看到 y 0 y_0 y0时是怎样的,假设此时已经计算出了从 y n + 1 y_{n+1} yn+1到 y 1 y_1 y1的非规范化概率向量 β 1 ( x ) \beta_1(x) β1(x)。从图中可以看出,它是汇聚到了 y 0 = start y_0=\text{start} y0=start的结点上,得到的是一个标量。
根据
(
p
6
)
(p6)
(p6)有:
Z
(
x
)
=
∑
y
1
M
1
(
y
0
=
start
,
y
1
∣
x
)
⋅
β
1
(
y
1
∣
x
)
=
M
1
(
y
0
=
start
,
y
1
=
1
∣
x
)
β
1
(
y
1
=
1
∣
x
)
+
M
1
(
y
0
=
start
,
y
1
=
2
∣
x
)
β
1
(
y
1
=
2
∣
x
)
+
⋯
+
M
1
(
y
0
=
start
,
y
1
=
m
∣
x
)
β
1
(
y
1
=
m
∣
x
)
\begin{aligned} Z(x) &= \sum_{y_1} M_1(y_0=\text{start},y_1|x) \cdot \beta_1(y_1|x) \\ &= M_1(y_0=\text{start},y_1=1|x) \beta_1(y_1=1|x) + M_1(y_0=\text{start},y_1=2|x) \beta_1(y_1=2|x) + \cdots + M_1(y_0=\text{start},y_1=m|x) \beta_1(y_1=m|x) \end{aligned}
Z(x)=y1∑M1(y0=start,y1∣x)⋅β1(y1∣x)=M1(y0=start,y1=1∣x)β1(y1=1∣x)+M1(y0=start,y1=2∣x)β1(y1=2∣x)+⋯+M1(y0=start,y1=m∣x)β1(y1=m∣x)
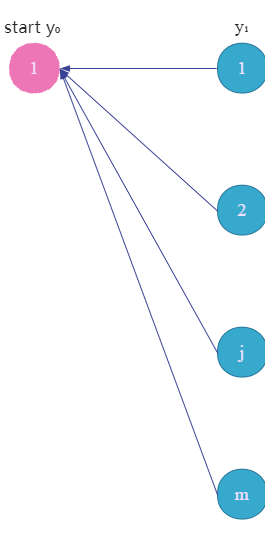
所以,最终
Z
(
x
)
Z(x)
Z(x)也可以写成向量化的形式:
Z
(
x
)
=
1
1
×
m
⋅
β
1
(
x
)
m
×
1
Z(x) = \pmb {1}_{1 \times m} \cdot \beta_1(x)_{m \times 1}
Z(x)=11×m⋅β1(x)m×1
这里的
1
\pmb 1
1是一个
1
×
m
1 \times m
1×m的列向量。
概率计算
有了前向后向算法,我们就可以很容易地计算序列在位置 i i i的标记是 y i y_i yi的条件概率。这在路径图中是这样的,这里假设 y i = j y_i=j yi=j状态。
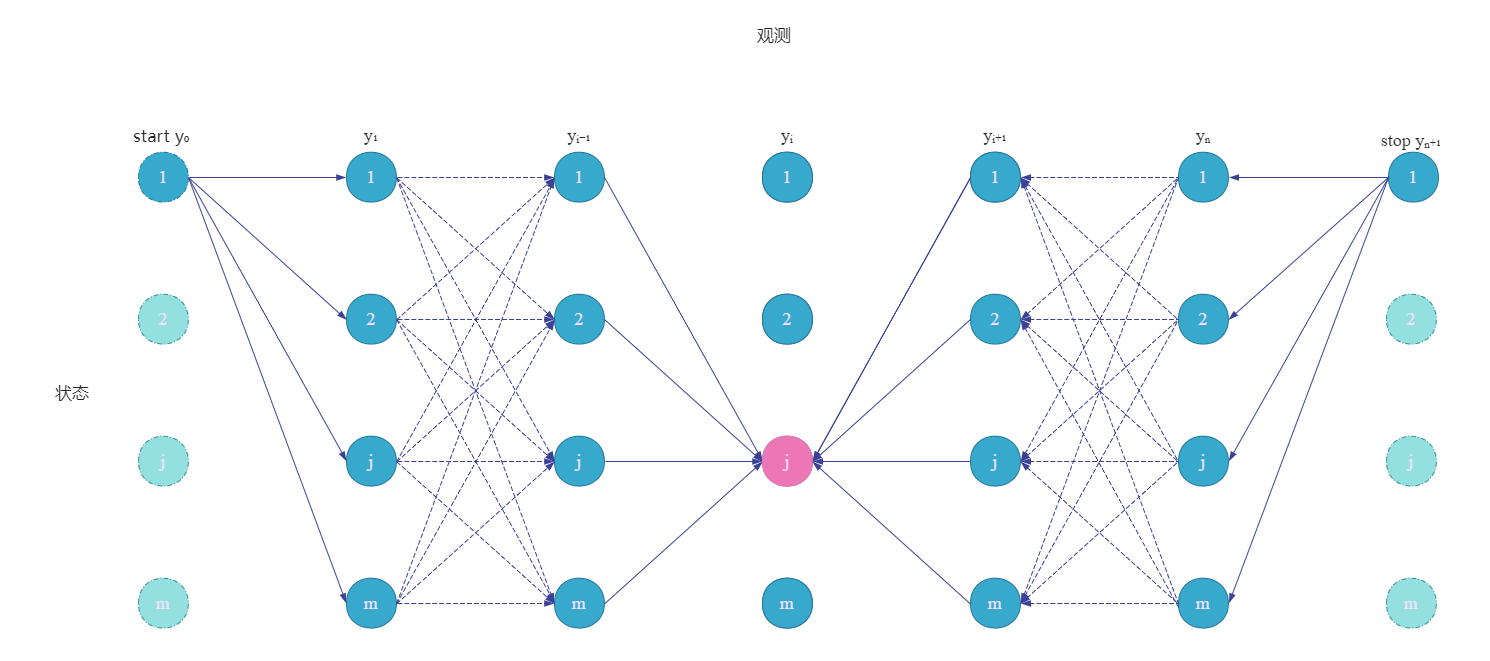
P ( Y i = y i ∣ x ) = α i T ( y i ∣ x ) β i ( y i ∣ x ) Z ( x ) (11.32) P(Y_i=y_i|x) = \frac{ \alpha_i^T(y_i|x)\beta_i(y_i|x)}{Z(x)} \tag{11.32} P(Yi=yi∣x)=Z(x)αiT(yi∣x)βi(yi∣x)(11.32)
也可以用公式推导证明,利用联合概率分布于边缘概率分布的关系有:
P
(
Y
i
=
y
i
∣
x
)
=
1
Z
(
x
)
∑
y
1
⋯
∑
y
i
−
1
∑
y
i
+
1
⋯
∑
y
n
∏
i
=
1
n
+
1
M
i
(
y
i
−
1
,
y
i
∣
x
)
=
1
Z
(
x
)
(
∑
y
1
⋯
∑
y
i
−
1
M
1
(
y
0
,
y
1
∣
x
)
M
2
(
y
1
,
y
2
∣
x
)
⋯
M
i
(
y
i
−
1
,
y
i
∣
x
)
)
(
∑
y
i
+
1
⋯
∑
y
n
M
i
+
1
(
y
i
,
y
i
+
1
∣
x
)
M
i
+
2
(
y
i
+
1
,
y
i
+
2
∣
x
)
⋯
M
n
+
1
(
y
n
,
y
n
+
1
∣
x
)
)
=
α
i
T
(
y
i
∣
x
)
β
i
(
y
i
∣
x
)
Z
(
x
)
\begin{aligned} P(Y_i=y_i|x) &= \frac{1}{Z(x)} \sum_{y_1} \cdots \sum_{y_{i-1}} \sum_{y_{i+1}} \cdots \sum_{y_n} \prod_{i=1}^{n+1} M_i(y_{i-1},y_i|x) \\ &= \frac{1}{Z(x)} \left(\sum_{y_1} \cdots \sum_{y_{i-1}} M_1(y_0,y_1|x) M_2(y_1,y_2|x) \cdots M_i(y_{i-1},y_i|x) \right) \left( \sum_{y_{i+1}} \cdots \sum_{y_n} M_{i+1}(y_{i},y_{i+1}|x) M_{i+2}(y_{i+1},y_{i+2}|x)\cdots M_{n+1}(y_n,y_{n+1}|x)\right) \\ &= \frac{\alpha_i^T(y_i|x)\beta_i(y_i|x)}{Z(x)} \end{aligned}
P(Yi=yi∣x)=Z(x)1y1∑⋯yi−1∑yi+1∑⋯yn∑i=1∏n+1Mi(yi−1,yi∣x)=Z(x)1(y1∑⋯yi−1∑M1(y0,y1∣x)M2(y1,y2∣x)⋯Mi(yi−1,yi∣x))(yi+1∑⋯yn∑Mi+1(yi,yi+1∣x)Mi+2(yi+1,yi+2∣x)⋯Mn+1(yn,yn+1∣x))=Z(x)αiT(yi∣x)βi(yi∣x)
下面计算标记是 y i − 1 y_{i-1} yi−1和 y i y_i yi的条件概率。
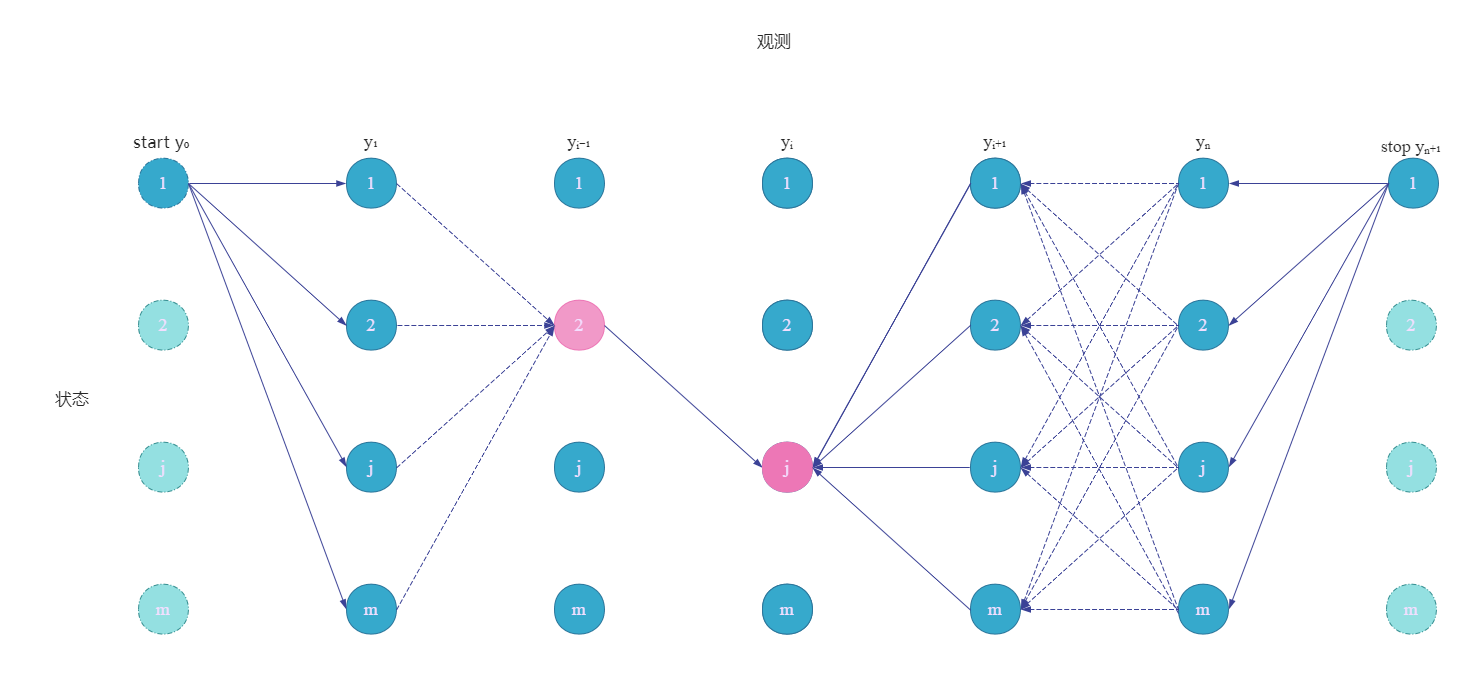
这里固定了 y i − 1 y_{i-1} yi−1和 y i y_i yi的状态,类似上图所示,同理,我们可以得到这个概率:
P ( Y i − 1 = y i − 1 , Y i = y i ∣ x ) = α i − 1 T ( y i − 1 ∣ x ) M i ( y i − 1 , y i ∣ x ) β i ( y i ∣ x ) Z ( x ) (11.33) P(Y_{i-1}=y_{i-1},Y_i=y_i|x) = \frac{ \alpha_{i-1}^T(y_{i-1}|x)M_i(y_{i-1},y_i|x)\beta_i(y_i|x)}{Z(x)} \tag{11.33} P(Yi−1=yi−1,Yi=yi∣x)=Z(x)αi−1T(yi−1∣x)Mi(yi−1,yi∣x)βi(yi∣x)(11.33)
期望值的计算
利用前向-后向向量,可以计算特征函数关于联合分布 P ( X , Y ) P(X,Y) P(X,Y)和条件分布 P ( Y ∣ X ) P(Y|X) P(Y∣X)的数学期望。
特征函数
f
k
f_k
fk关于条件分布
P
(
Y
∣
X
)
P(Y|X)
P(Y∣X)的数学期望是
E
P
(
Y
∣
X
)
[
f
k
]
=
∑
y
P
(
Y
∣
X
)
f
k
(
y
,
x
)
=
∑
i
=
1
n
+
1
∑
y
i
−
1
,
y
i
f
k
(
y
i
−
1
,
y
i
,
x
,
i
)
α
i
−
1
T
(
y
i
−
1
∣
x
)
M
i
(
y
i
−
1
,
y
i
∣
x
)
β
i
(
y
i
∣
x
)
Z
(
x
)
(11.34)
\begin{aligned} E_{P(Y|X)}[f_k] &= \sum_y P(Y|X) f_k(y,x) \\ &= \sum_{i=1}^{n+1} \sum_{y_{i-1},y_i} f_k(y_{i-1},y_i,x,i) \frac{ \alpha_{i-1}^T(y_{i-1}|x)M_i(y_{i-1},y_i|x)\beta_i(y_i|x)}{Z(x)} \end{aligned} \tag{11.34}
EP(Y∣X)[fk]=y∑P(Y∣X)fk(y,x)=i=1∑n+1yi−1,yi∑fk(yi−1,yi,x,i)Z(x)αi−1T(yi−1∣x)Mi(yi−1,yi∣x)βi(yi∣x)(11.34)
其中,
k
=
1
,
⋯
,
K
k=1,\cdots,K
k=1,⋯,K;
假设经验分布为
P
~
(
X
)
\tilde P(X)
P~(X),即用经验分布代替真实分布,那么特征函数
f
k
f_k
fk关于联合分布
P
(
X
,
Y
)
P(X,Y)
P(X,Y)的数学期望是
E
P
(
X
,
Y
)
[
f
k
]
=
∑
x
,
y
P
(
x
,
y
)
∑
i
=
1
n
+
1
f
k
(
y
i
−
1
,
y
i
,
x
,
i
)
=
∑
x
,
y
P
(
x
)
P
(
y
∣
x
)
∑
i
=
1
n
+
1
f
k
(
y
i
−
1
,
y
i
,
x
,
i
)
=
∑
x
P
~
(
x
)
∑
y
P
(
y
∣
x
)
∑
i
=
1
n
+
1
f
k
(
y
i
−
1
,
y
i
,
x
,
i
)
=
∑
x
P
~
(
x
)
∑
i
=
1
n
+
1
∑
y
i
−
1
,
y
i
f
k
(
y
i
−
1
,
y
i
,
x
,
i
)
α
i
−
1
T
(
y
i
−
1
∣
x
)
M
i
(
y
i
−
1
,
y
i
∣
x
)
β
i
(
y
i
∣
x
)
Z
(
x
)
(11.35)
\begin{aligned} E_{P(X,Y)} [f_k] &= \sum_{x,y} P(x,y) \sum_{i=1}^{n+1} f_k(y_{i-1},y_i,x,i) \\ &= \sum_{x,y} P(x) P(y|x) \sum_{i=1}^{n+1} f_k(y_{i-1},y_i,x,i) \\ &= \sum_x \tilde P(x) \sum_{y} P(y|x) \sum_{i=1}^{n+1} f_k(y_{i-1},y_i,x,i) \\ &= \sum_x \tilde P(x) \sum_{i=1}^{n+1} \sum_{y_{i-1},y_i} f_k(y_{i-1},y_i,x,i) \frac{ \alpha_{i-1}^T(y_{i-1}|x)M_i(y_{i-1},y_i|x)\beta_i(y_i|x)}{Z(x)} \end{aligned} \tag{11.35}
EP(X,Y)[fk]=x,y∑P(x,y)i=1∑n+1fk(yi−1,yi,x,i)=x,y∑P(x)P(y∣x)i=1∑n+1fk(yi−1,yi,x,i)=x∑P~(x)y∑P(y∣x)i=1∑n+1fk(yi−1,yi,x,i)=x∑P~(x)i=1∑n+1yi−1,yi∑fk(yi−1,yi,x,i)Z(x)αi−1T(yi−1∣x)Mi(yi−1,yi∣x)βi(yi∣x)(11.35)
其中,
k
=
1
,
⋯
,
K
k=1,\cdots,K
k=1,⋯,K;