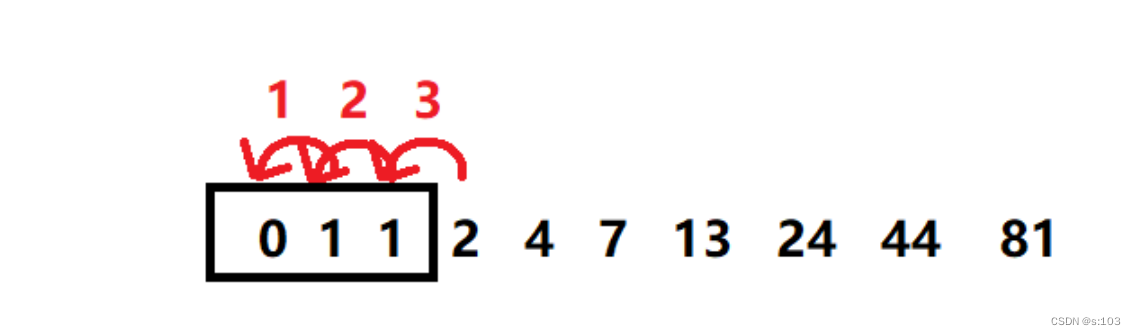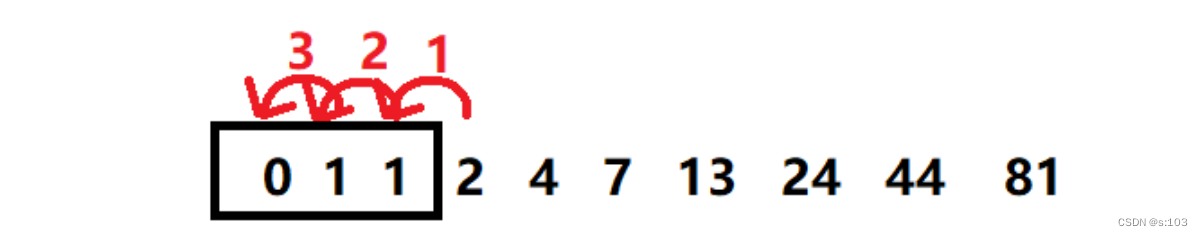冻龟算法系列之斐波那契数列模型

文章目录

• 【动态规划】斐波那契数列模型
• • 1. 第N个泰波那契数
  • • 1.1 题目解析
    • 1.2 算法原理
    • • 1.2.1 状态表示
      • 1.2.2 状态转移方程
      • 1.2.3 初始化
      • 1.2.4 填表顺序
      • 1.2.5 返回值
    • 1.3 编写代码
    • 1.4 空间优化
  • 2. 三步问题
  • • 2.1 题目解析
    • 2.2 算法原理
    • • 2.2.1 状态表示
      • 2.2.2 状态转移方程
      • 2.2.3 初始化
      • 2.2.4 填表顺序
      • 2.2.5 返回值
    • 2.3 编写代码
  • 3. 使用最小花费爬楼梯
  • • 3.1 题目解析
    • 3.2 算法原理
    • • 3.2.1 状态表示
      • 3.2.2 状态转移方程
      • 3.2.3 初始化
      • 3.2.4 填表顺序
      • 3.2.5 返回值
    • 3.3 编写代码
    • 3.4 解法2：以某节点为起点
    • • 3.4.1 得到状态转移方程
      • 3.4.2 初始化
      • 3.4.3 编写代码
  • 4. 解码方法
  • • 4.1 题目解析
    • 4.2 算法原理
    • • 4.2.1 状态表示
      • 4.2.2 状态转移方程
      • 4.2.3 初始化
      • 4.2.4 填写顺序
      • 4.2.5 返回值
    • 4.3 编写代码
    • 4.4 代码简化技巧

【动态规划】斐波那契数列模型

动态规划（英语：Dynamic programming，简称 DP），是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题。

至于这个模型是什么意思，我觉得你往下看下去，自主感受那些相似之处，才不会懵逼~

而本文为动态规划系列的第一篇，所以在动态规划做题步骤上会比较分明，接下来的几道例题，让我们边实战边学吧！
文章解题的大的流程为：

1. 题目解析
2. 算法原理（可能会有其他解法，在这个系列只讲解动态规划的思想）
3. 编写代码
4. 空间优化
   • 动态规划一般很难，做出来已经不错了，所以主要重心放在解题上
   • 本文第一道题，把所有流程都会过一遍，所以会讲，而在讲背包问题之前，都不会出现这个步骤
   • 因为动态规划一般会比较浪费空间，所以才有这个空间优化的必要

1. 第N个泰波那契数

传送门：力扣1137

题目：

1.1 题目解析

所以有以下示例：

同理：

1.2 算法原理

算法原理分析的过程分五步：

1. 画出dp表并确定dp表**状态表示**
2. 根据状态表示确定**状态转移方程**
3. **初始化**dp表
4. 确定**填表顺序**
5. 确定**返回值**

由于是第一道题，所以下面是细致讲解！

• 但是因为这道题比较简单，一些方面没有涉及到，但是对于初学者，这样才最友好，因为本题重点就是熟悉做题流程！
• 在后续的学习中，反复积累经验，了解方方面面，再依此基础上去刷题，才能学好动态规划！

1.2.1 状态表示

什么是状态表示：

这就涉及动态规划的核心：dp表

• 这个dp表的建立是不固定的，可能是一维数组，二维数组等等…

而dp表中的元素与其对应下标有什么关系，即这个元素的**含义**，或者说是这个元素所处的“状态”（抽象笼统的说法）

• 而其中，我们要的答案，就是dp表其中的一个元素

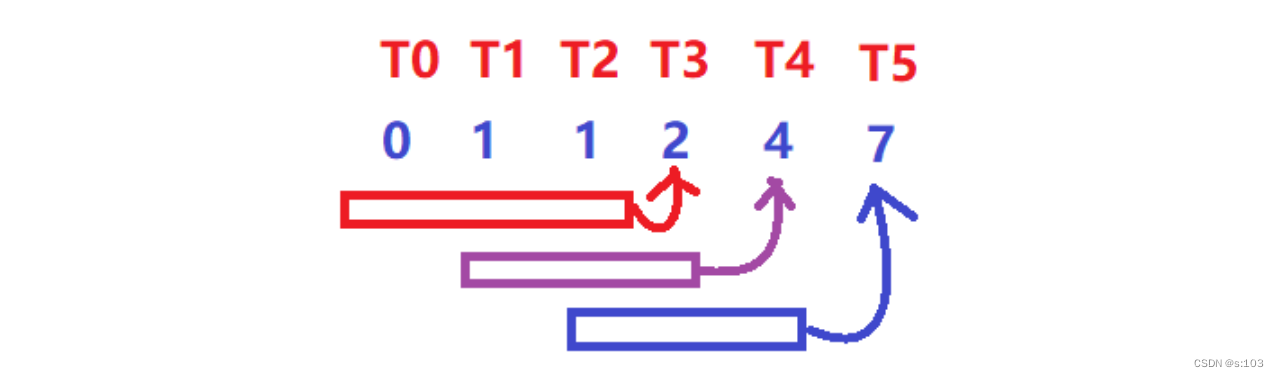
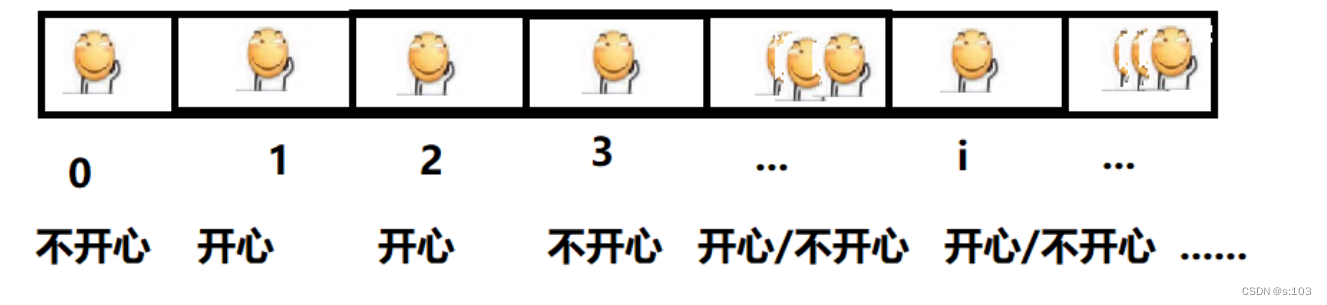
例子：

• 开心or不开心，是状态
• 1下标元素的含义就是滑稽老铁开心

• 当然，dp表代表的状态一般不是对立的，而是这样的

• 而之后我们可以 以“含义”去理解

而设立的状态表示不一样，也意味着思路不一样，即不同的解法~

• 想到一个，然后就去试试能不能解…
• 做多点题，这一步准确率会高点~

怎么来？

1. 经验 + 题目要求
2. 分析问题的过程中，发现重复的子问题，抽象成状态表示（暂时不讲）

而这道题，我们只需建立一个一维dp表（大小为n + 1）：

1. 题目要求：返回第n个泰波那契数的值
2. 经验：dp[n]应该就是答案

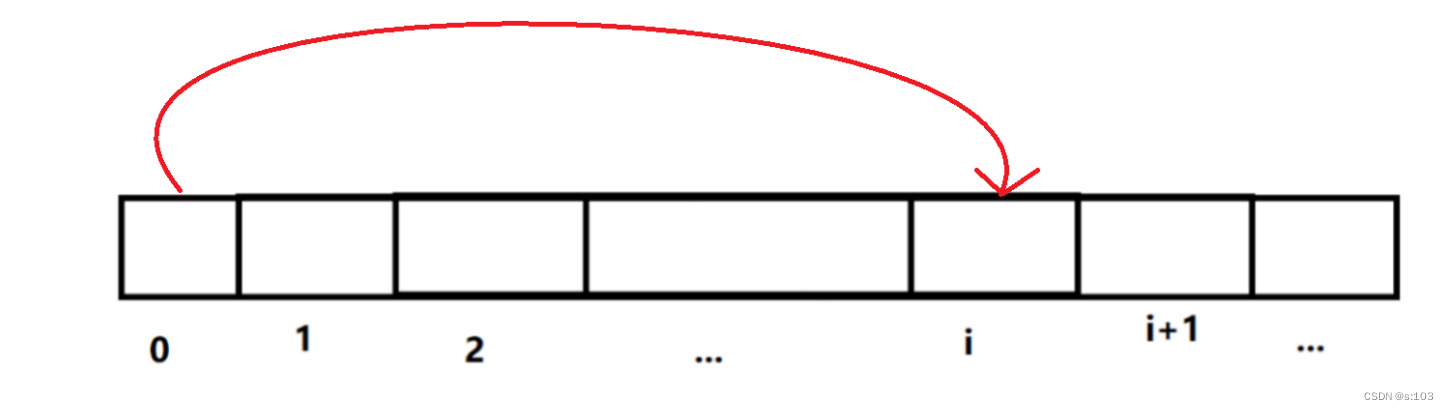
即dp[i]表示：第 i 个泰波那契数的值

1.2.2 状态转移方程

什么是**状态转移方程**：

• 就是，dp[i] = … ;
• 而这个方程可能有条件，分支，循环等复杂的逻辑…

而dp[i]是由dp表其他下标对应的值来推导出来的

• 比如，dp[i]之前或者之后的值可以推出dp[i]

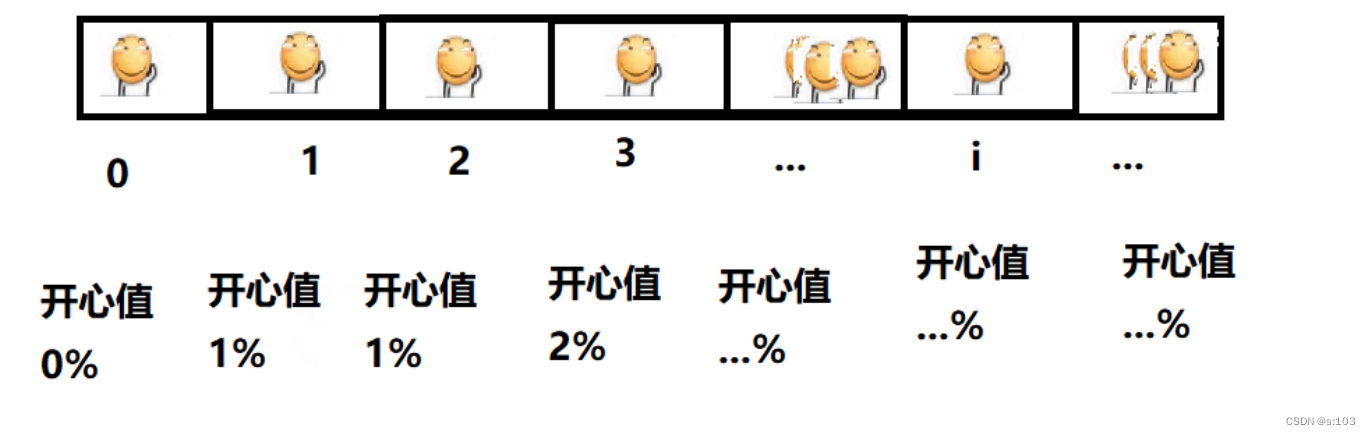
例子：

• 开心是会传染的：

而本题的动态转移方程就是：

dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];

• 难的方程怎么推导？
  • 遇到再说
  • 现在纸上谈兵没有意义

对应动态规划的题目而言，前两步是最最重要的，也就是百分之99已完成~

接下来就是一些细节的处理

1.2.3 初始化

• 很明显，通过已知推未知的过程中，会遇到一些数组越界等问题…，而初始化就是为了解决这些问题

本题为：

• i - 1，i - 2，i - 3要有意义，则i要大于等于3
• 所以在初始化的时候，手动给dp[0]、dp[1]、dp[2]赋值（赋值之前要确保不越界，越界就直接返回即可）

1.2.4 填表顺序

我们通过已知推未知，这里的已知可能是i之前或者i之后，这就分为了简单的两个大方向（一维dp表）

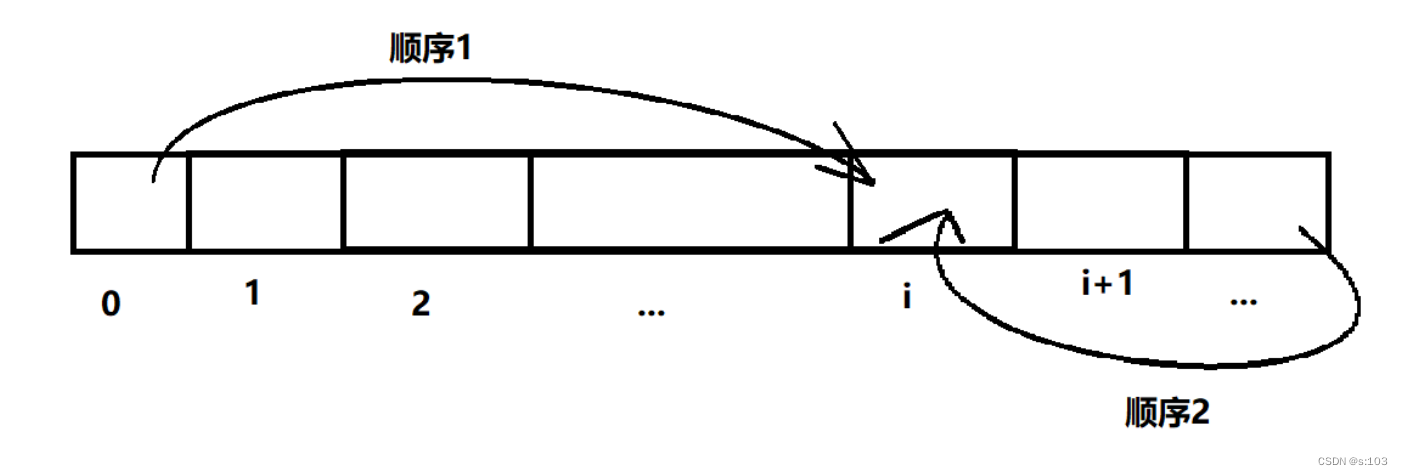
本题为：顺序1

• 要保证填这个下标的时候，需要用到的其他下标，是已经在此之前填了的！
  • 即，计算过了的

1.2.5 返回值

根据题目要求 + 状态表示得出返回值

本题为：dp[n]

• 注意下标确定是哪个
• 可以说返回值和状态表示是同时确定的

1.3 编写代码

编写代码分为固定的四步：

1. 创建dp表
2. 初始化
3. 算法主体（填表）
4. 返回值

class Solution {
    public int tribonacci(int n) {
        //1. 创建dp表
        int[] dp = new int[n + 1];
        //2. 初始化
        if(n == 0) {
            return 0;
        }
        if(n == 1 || n == 2) {
            return 1;
        }
        dp[0] = 0;
        dp[1] = 1;
        dp[2] = 1;
        //3. 填表
        for(int i = 3; i < n + 1; i++) {
            dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];
        }
        //4. 返回值
        return dp[n];
    }   
}

1. 由于我们要访问到dp[n]并返回，所以dp表的大小为n + 1
2. 初始化之前要进行判断，否则会数组越界
3. 通过状态转移方程来填表
4. 返回dp[n]

在提交之前测试一下，可以自行输入实例去测~

可见空间复杂度和时间复杂度都为O(N)

1.4 空间优化

通过“滚动数组”去进行空间优化

• O(N²) => O(N)
• O(N) => O(1)

算法修改思想：

• 计算dp[i]其实只需要用到dp[i - 1] + dp[i - 2] + dp[i - 3]，其实一直都是用三块空间，所以我们只需要反复使用则三块空间就行了

class Solution {
    public int tribonacci(int n) {
        //1. 空间优化
        int[] src = new int[3];
        src[0] = 0;
        src[1] = 1;
        src[2] = 1;
        
        //2. 初始化
        if(n == 0) {
            return 0;
        }
        if(n == 1 || n == 2) {
            return 1;
        }
        int ret = 0;
        
        //3. 填表
        for(int i = 3; i < n + 1; i++) {
            ret = src[0] + src[1] + src[2];
            src[0] = src[1];
            src[1] = src[2];
            src[2] = ret;
        }
        //4. 返回值
        return ret;
    }   
}

赋值操作则是这样的：

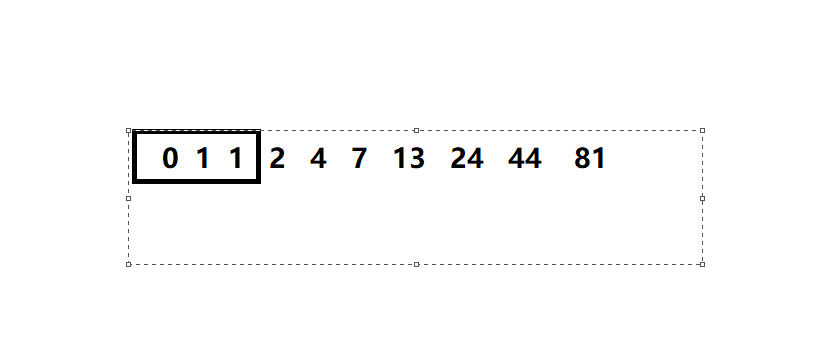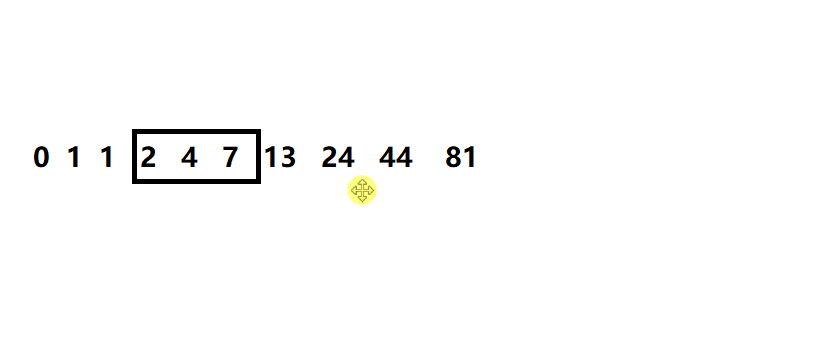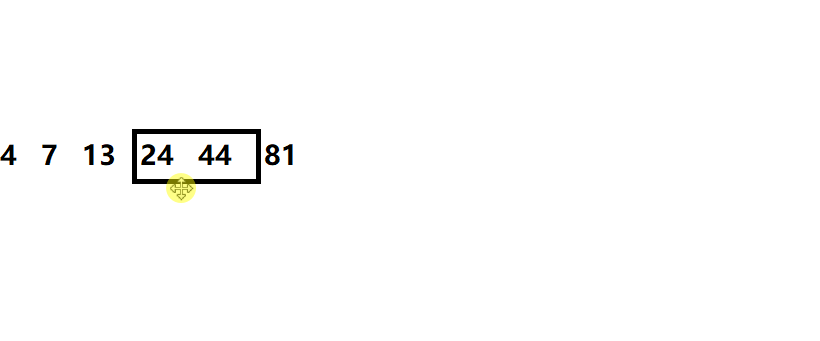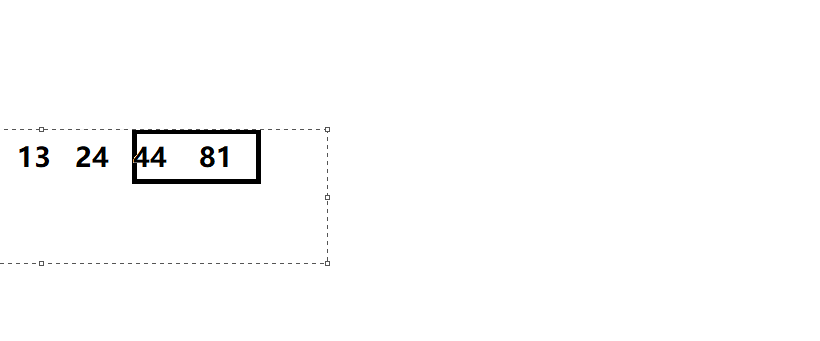
则就从头部挪，而不是从尾部挪

从头部开始挪：

• 正常

从尾部开始挪：

• 异常，最终三个值都为2

第一道题就这样愉快的结束了，想必你已经了解了动态规划作答的流程了，接下来就是做几道题，走几遍流程，好好感受它“动归思想”~

2. 三步问题

传送门：面试题08.01.

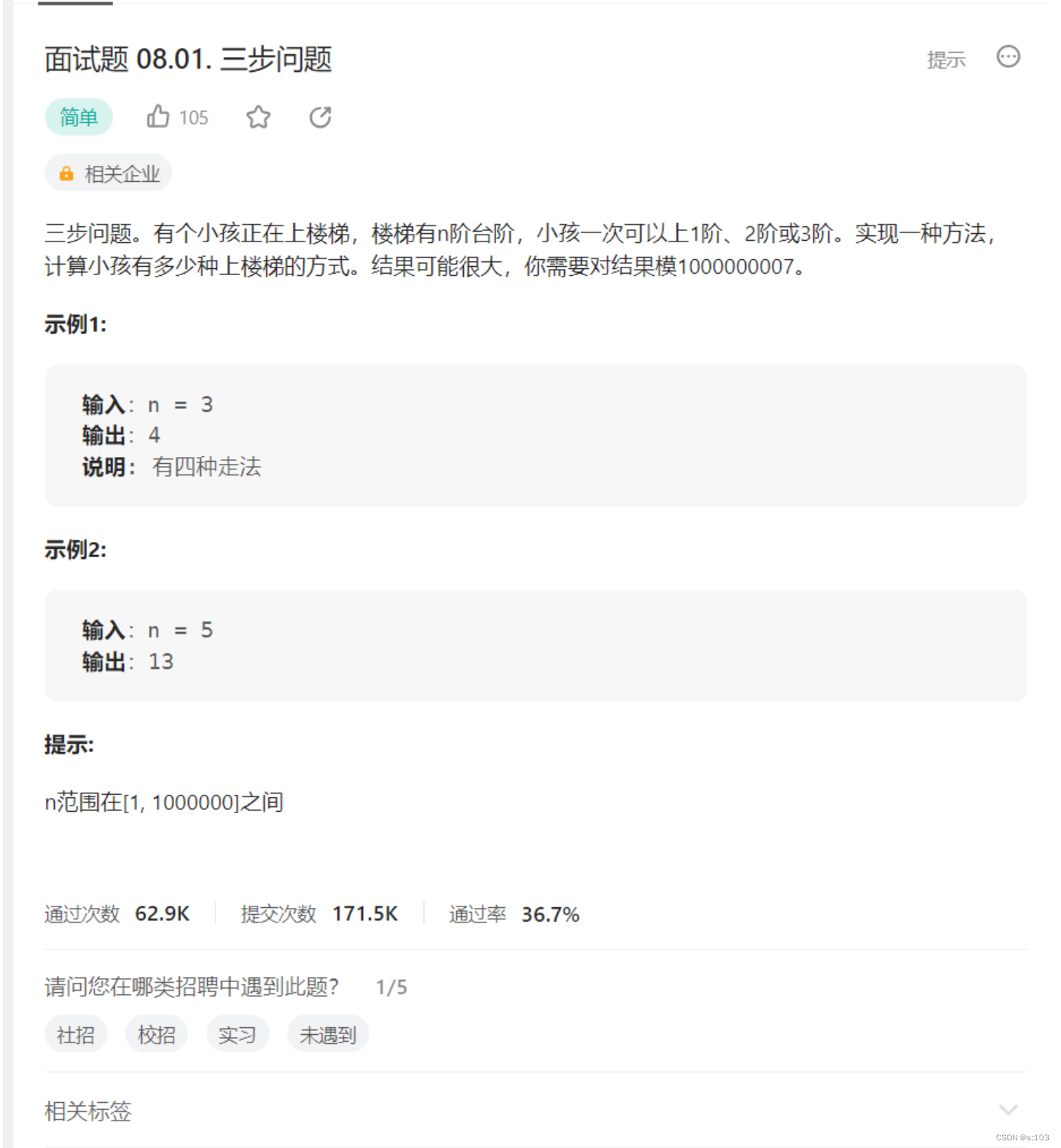
题目：

2.1 题目解析

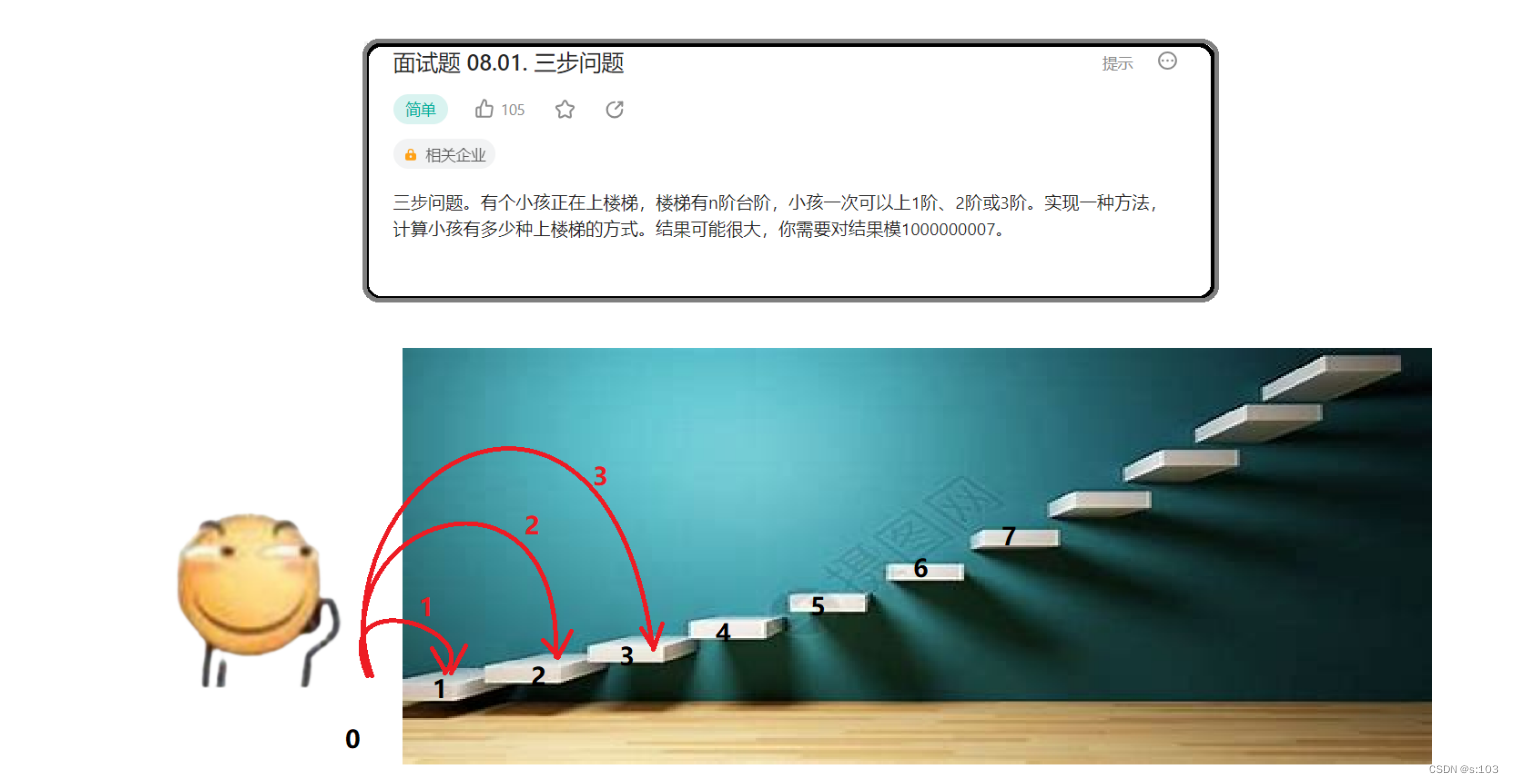
• 小明一次可以跨1、2、3步~

输入一个数n，求出从0到n的爬法数

通过示例探索规律：

• 并且结果要模上1e9 + 7！
  • 1eN = 1.0 × 10^N，所以这个值为浮点型
  • 一般我们习惯定义一个int型常数DOM 等于这里的1eN；

2.2 算法原理

2.2.1 状态表示

很显然，这要用到一维的顺序结构，dp表的大小为n + 1

题目要求：

• 返回到达第n个台阶的爬法数

经验：以某个节点为结尾或者以某个节点为起点去研究问题

• 此题就是以第i个节点为结尾，用 i 之前的节点推导出第 i 个节点的值
• 结果应该为dp[n]（dp表其中一值）

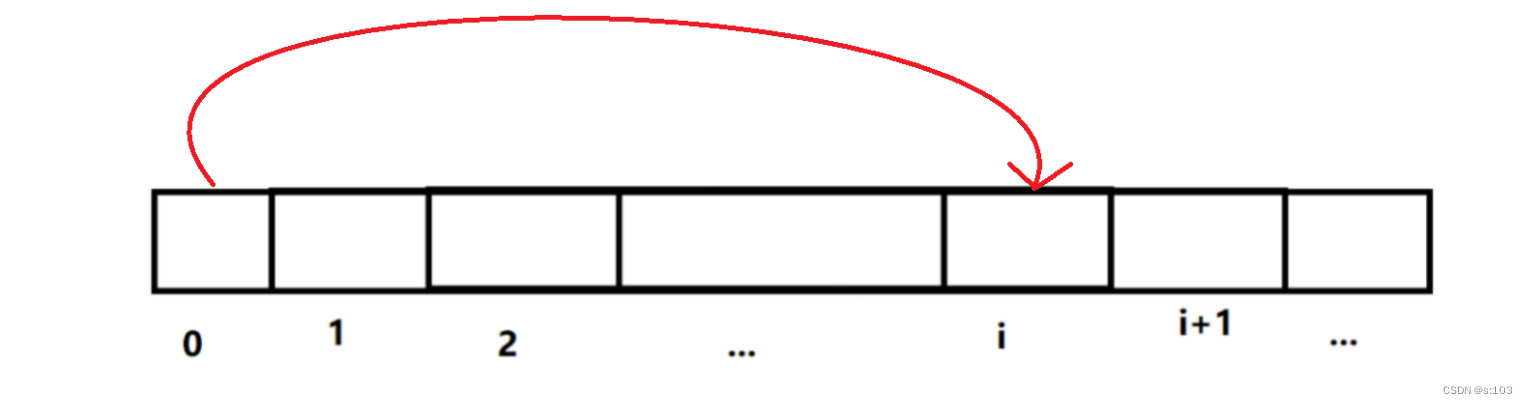
得出dp表元素dp[i]的含义就是，到达第 i 个台阶的爬法数

2.2.2 状态转移方程

而得出状态转移方程的思想就是：借用“已知”状态！

• 我们就幻想dp[i]之前的值，是已知，则有以下操作

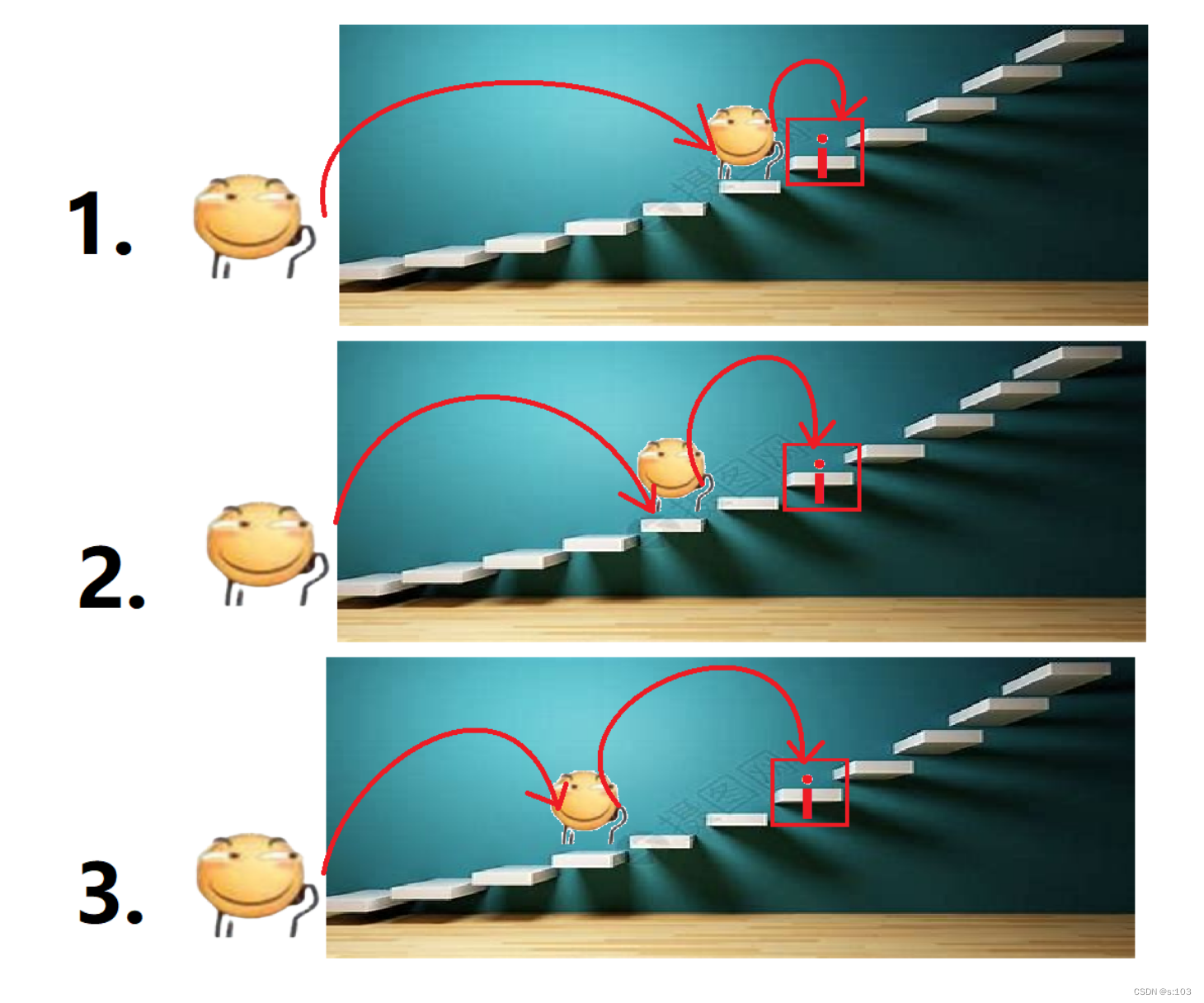
我们要到达 i，那么我们到达前的位置可以是：i - 1，i - 2，i - 3：

1. 到达i - 1，有dp[i - 1]种爬法，然后跳三步到达 i
2. 到达i - 2，有dp[i - 2]种爬法，然后跳两步到达 i
3. 到达i - 3，有dp[i - 3]种爬法，然后跳一步到达 i

到达i - 1可以跳两步在跳一步或者跳一步再跳两步之类的啊

• 没错，但是这包含在情况2和情况3中（到达i -2 或者 到达 i - 3）
  

所以得出dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]

• 变成泰波那契数列了~

可以通过示例验证一下想法：

2.2.3 初始化

同样的，i - 3 、i - 2、i - 1 需要考虑数组越界的问题~

2.2.4 填表顺序

dp[i]之前是已知，则填表应从左到右~

2.2.5 返回值

返回dp[n]~

2.3 编写代码

一样的，分为四步：

1. 创建dp表
2. 初始化
3. 填表
4. 返回值

class Solution {
    public int waysToStep(int n) {
        //1. 创建表
        int[] dp = new int[n + 1];
        int MOD = (int)1e9 + 7; //取模数

        //2. 初始化，处理边界问题
        if(n == 1) {
            return 1;
        }
        if(n == 2) {
            return 2;
        }
        if(n == 3) {
            return 4;
        }
        dp[1] = 1;
        dp[2] = 2;
        dp[3] = 4;

        //3. 填表
        for(int i = 4; i < n + 1; i++) {
            dp[i] = ((dp[i - 1] + dp[i - 2]) % MOD + dp[i - 3]) % MOD;
        }

        //4. 返回值
        return dp[n];
    }
}

• 没做一次加法就要取模一次！
• 因为取模满足分配律，所以这样子算得到的结果没问题

3. 使用最小花费爬楼梯

传送门：力扣746

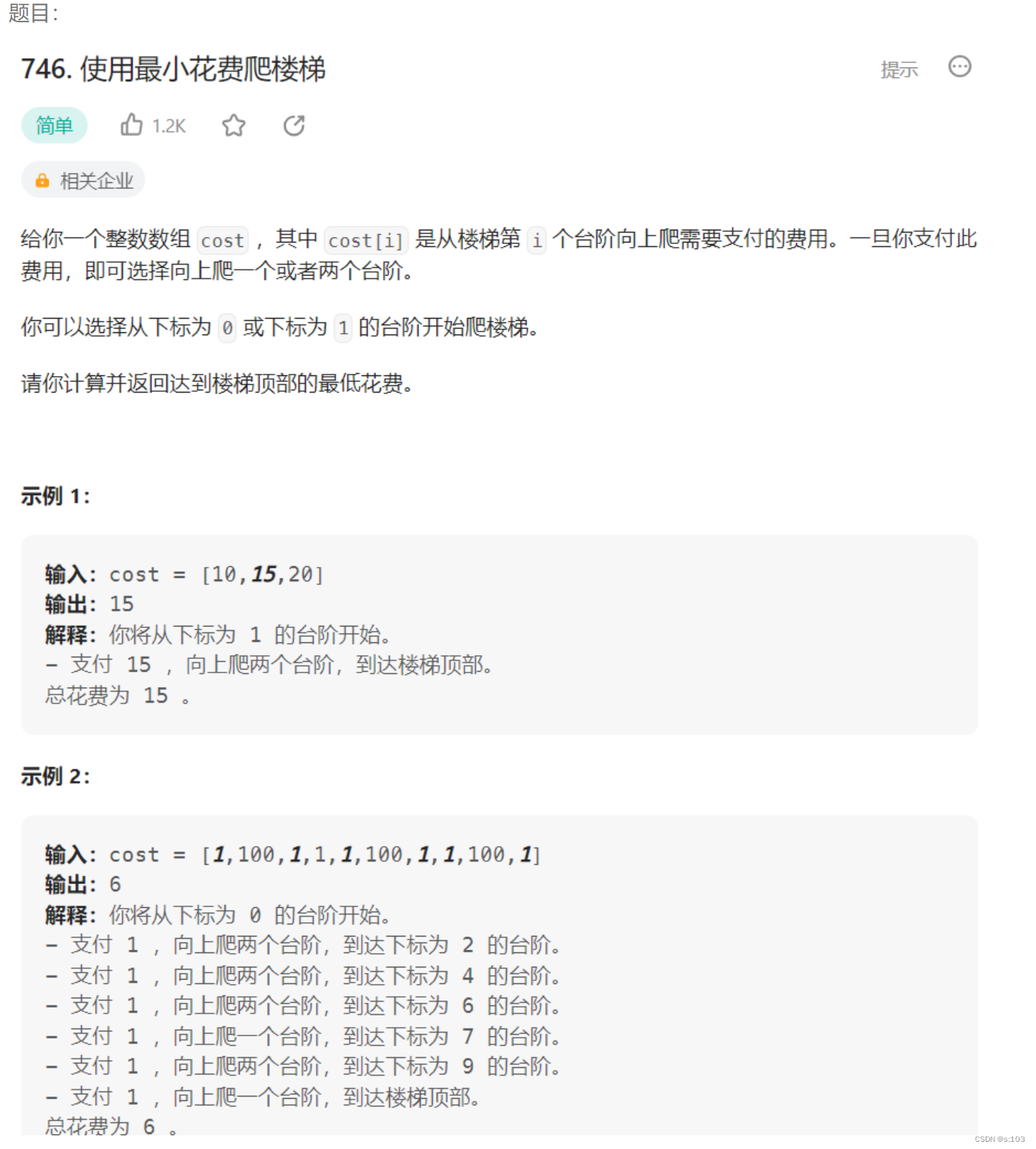
题目：

3.1 题目解析

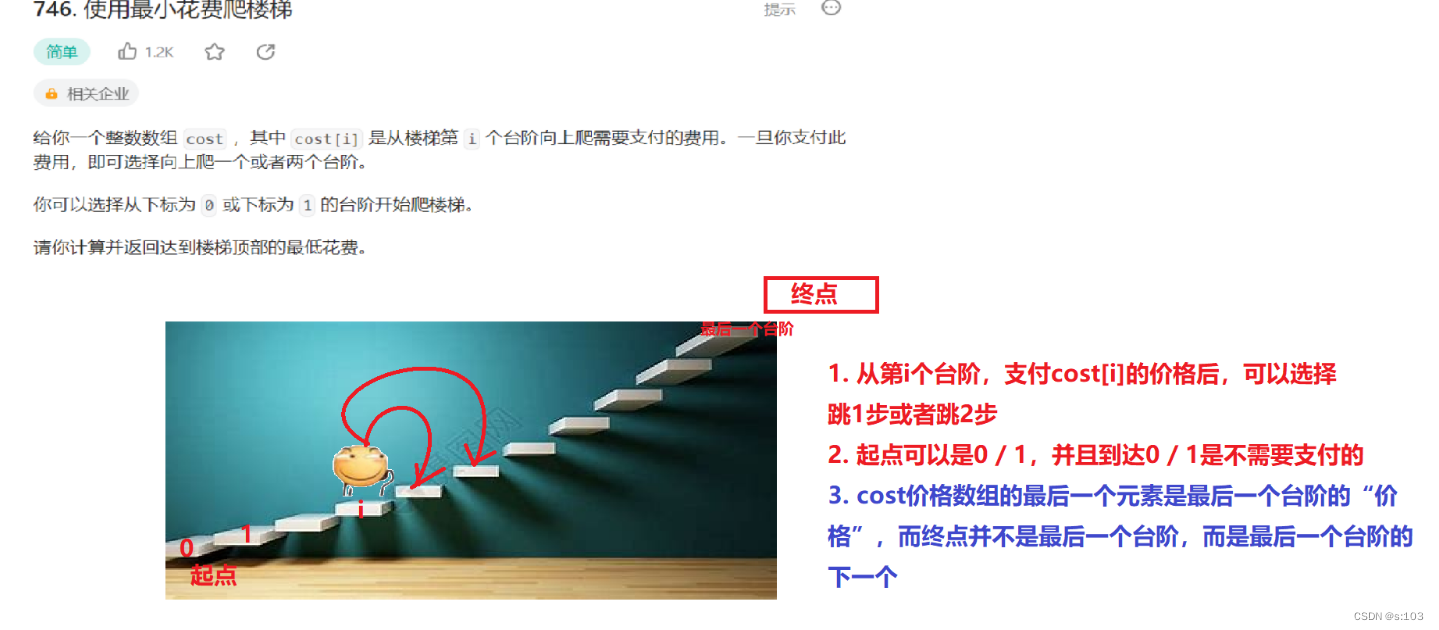
输入一个cost数组，通过数组得到付费台阶数n，得到终点位置，输出到达终点的最小花费

通过示例探索规律：

3.2 算法原理

3.2.1 状态表示

很显然，这要用到一维的顺序结构

且dp数组的大小为n + 1

题目要求：返回到达终点的最小花费（理解为到达第n个台阶）

经验：以某一个节点为终点或者以某一个节点为起点去研究

• 而答案应该对应到dp表中的dp[n]（其中一值）
• 这道题也因此分离出两种解法（先将以某节点为终点的解法）

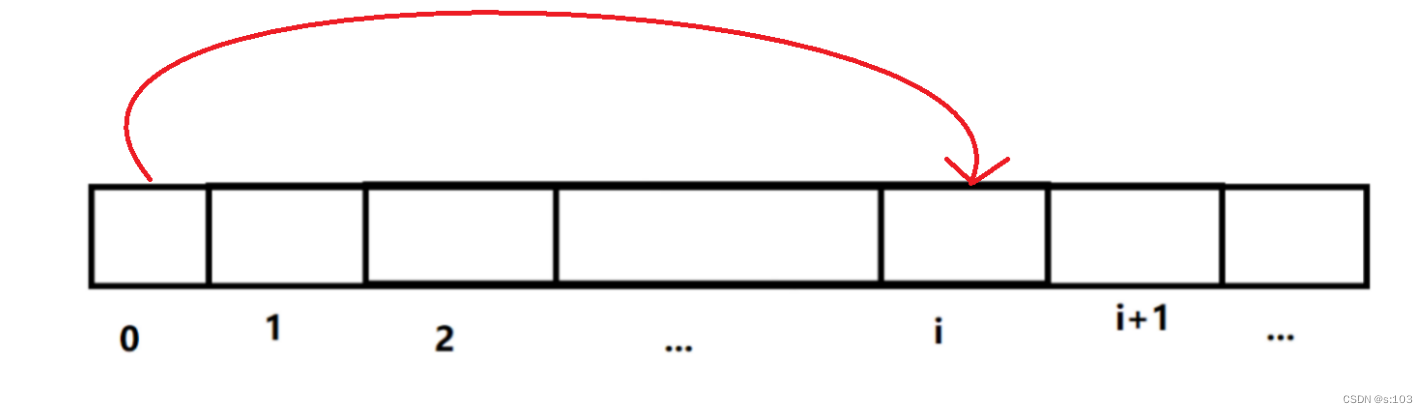
所以状态表示就是：dp[i]代表从起点到 i 的最小消费

3.2.2 状态转移方程

同样的，把dp[i]之前的值认为“已知”，以此为条件去推导dp[i]

我们要到达 i，那么我们到达前的位置可以是：i - 1，i - 2

1. 到达i - 1，在原来支付的dp[i - 1]的基础上支付cost[i - 1]，跳一步到dp[i]
2. 到达i - 2，在原来支付的dp[i - 2]的基础上支付cost[i - 2]，跳两步到dp[i]

而我们需要取其较小值~

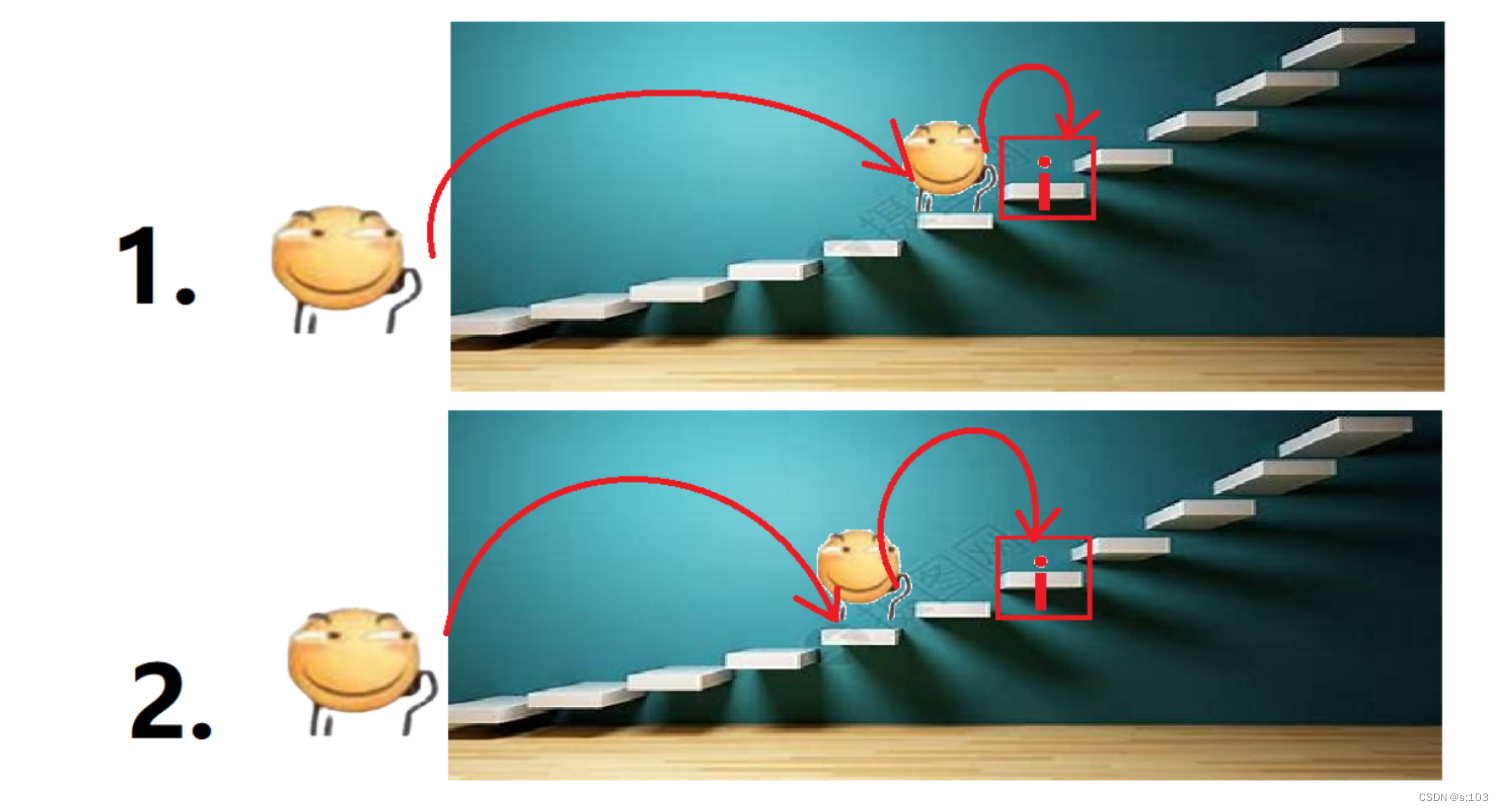
所以得到，dp[i] = min{dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]}

3.2.3 初始化

对于0和1下标要进行一些初始化~

到达0和1并不需要支付，所以值为0~

3.2.4 填表顺序

由于是以i节点为终点，dp[i]之前的点为条件，所以顺序为左到右

3.2.5 返回值

返回dp[n]，其代表第n个台阶（终点）的最小花费~

3.3 编写代码

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int n = cost.length;
        //1. 创建dp表   
        int[] dp = new int[n + 1];
        //2. 初始化，处理边界
        if(n == 0 || n == 1) {
            return 0;
        }
        dp[0] = 0;
        dp[1] = 0;
        //3. 填表
        for(int i = 2; i < n + 1; i++) {
            dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
        }
        //4. 返回值
        return dp[n];
    }
}

• 直接根据刚才的算法分析写就行了~
  

3.4 解法2：以某节点为起点

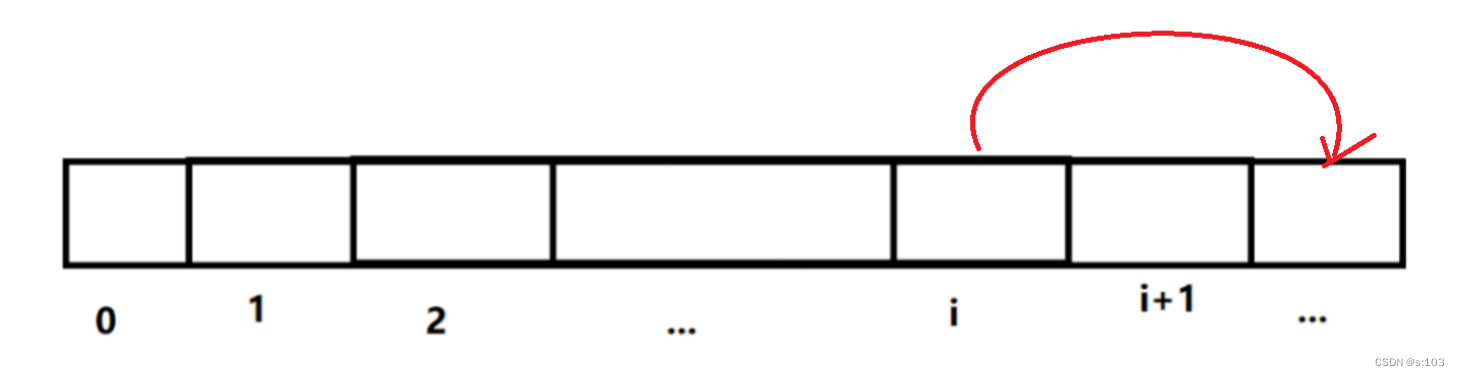
得到状态表示为：dp[i] 代表 第i个台阶跳到终点的最小花费

• 所以返回值为dp[0] 或者dp[1]的最小值
• 填表顺序为从右往左

3.4.1 得到状态转移方程

我们认定从dp[i]以后的值为“已知”，利用它们得到结果，从第i个台阶到终点的接下来的一步，要么到达i + 1,要么到达i + 2：

1. 到达i + 1，支付cost[i]的基础上支付dp[i + 1]后到达终点
2. 到达i + 2，支付cost[i]的基础上支付dp[i + 2]后到达终点

并且取其较小值最为dp[i]

所以方程为：dp[i] = min{dp[i + 1], dp[i + 2]} + cost[i];

3.4.2 初始化

dp[n]为终点，值为0

dp[n - 1]到终点只有一步之遥，值为cost[n - 1]

3.4.3 编写代码

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int n = cost.length;
        //1. 创建dp表   
        int[] dp = new int[n + 1];
        //2. 初始化，处理边界
        if(n == 0 || n == 1) {
            return 0;
        }
        dp[n] = 0;
        dp[n - 1] = cost[n - 1];
        //3. 填表
        for(int i = n - 2; i >= 0; i--) {
            dp[i] = Math.min(dp[i + 1], dp[i + 2]) + cost[i];
        }
        //4. 返回值
        return Math.min(dp[0], dp[1]);
    }
}

所以状态表示的不同，算法思路就有所不同，至于怎么选中呢？

1. 做题多，经验多
2. 想到一个，就想尽方法去用这一个去解决问题，解决不了再换（敢于尝试）

4. 解码方法

传送门：力扣91

题目：

4.1 题目解析

对于示例，目前看不出什么~

4.2 算法原理

4.2.1 状态表示

显然，也是一维的dp表（大小为n）

题目要求：输入字符串，返回整个字符串能反解出来的解的个数

经验：以某个节点为终点

• 那么这个终点只能是字符串的某个字符了~
• 而答案应该为dp[n - 1]（dp表的其中一值）

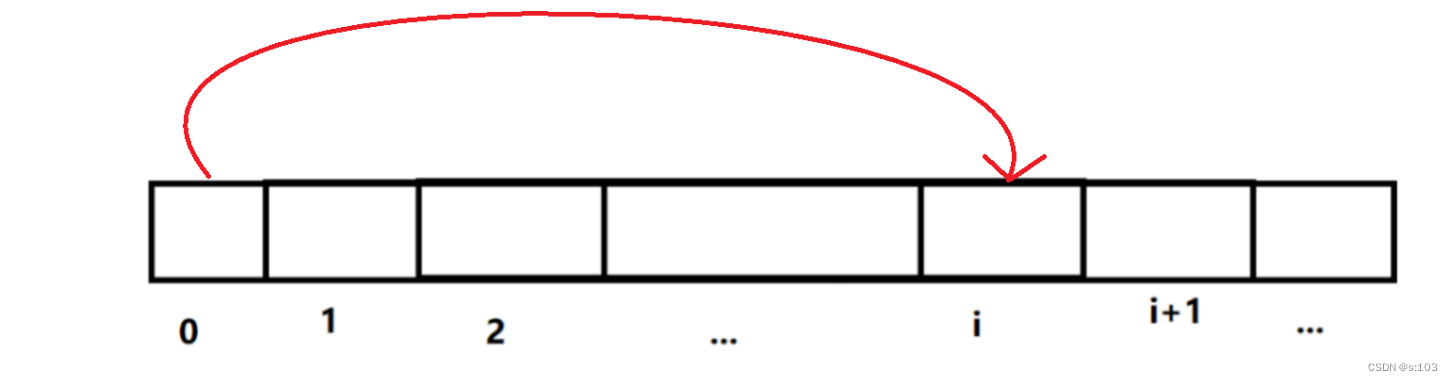
那么我们趋向于让答案合理的为dp[n - 1]:

得到状态表示：dp[i]代表字符串[0, i]的子串最多能反解出来的解的个数

4.2.2 状态转移方程

同样的，我们把dp[i]之前的值视为“已知”，把它们当做条件，去推导dp[i]

那么，要扩展到[0, i]的字符串，则扩展成[0, i]字符串之前，应该为[0, i - 1]的子串或者[0, i - 2]的子串:

1. 如果是[0, i - 1]的子串，则字符串的第i个字符应该单独转化为字母才行，不然前功尽弃！
   • 反解成功：dp[i - 1]
   • 反解失败：0
2. 如果是[0, i - 2]的子串，则字符串的第i - 1和第i个字符应该成双转化为字母(06之类的不行！)才行，否则前功尽弃！
   • 反解成功：dp[i - 2]
   • 反解失败：0
   • 为什么不可以各自可转化为字母也行?
     • 第i - 1个字符可以单独反解和第i个字符也可以单独反解，此解法在情况1出现过

得出状态转移方程：

dp[i] = (dp[i - 1]) + (dp[i - 2]);

• 前提是对应项满足条件

4.2.3 初始化

对于0和1下标要特殊处理：

• 0的话

  1. 如果可以单独成字母 => 1
  2. 不可以 => 0

• 1的话

  1. 成双结合成字母 => +1
  2. 各自单独成字母 => +1
  3. 都不可以 => 0

4.2.4 填写顺序

由于是以某个节点为终点，所以填写顺序为从左到右~

4.2.5 返回值

返回dp[n - 1]，代表整个字符串能反解的解的个数

4.3 编写代码

class Solution {
    public int numDecodings(String s) {
        int n = s.length();

        char[] string = s.toCharArray();        
        //创建dp表
        int[] dp = new int[n];
        //初始化并处理边界问题
        if(string[0] != '0') {
            dp[0] = 1;
        }
        if(n == 1) {
            return dp[0];
        }
        if(string[0] !='0' && string[1] != '0') {
            dp[1]++;
        }
        int number = (string[0] - '0') * 10 + string[1] - '0';
        if(number >= 10 && number <= 26) {
            dp[1]++;
        }
        for(int i = 2; i < n; i++) {
            if(string[i] != '0') {
                dp[i] += dp[i - 1];
            }
            number = (string[i - 1] - '0') * 10 + string[i] - '0';
            if(number >= 10 && number <= 26) {
                dp[i] += dp[i - 2];
            }
        }
        return dp[n - 1];
    }
}

• 总体代码跟刚才的原理对应，理解起来也没啥问题
• 但是明显的，这个初始化未免也太长了吧~

而且，跟填表操作还差不多：

• 写得很别扭~
  

4.4 代码简化技巧

• 这就衍生出一种做法，就是在添加一个“假的数据“，而这个假的数据仍让状态转移方程成立~
• 这样就可以将重复的代码放在一起了~
  

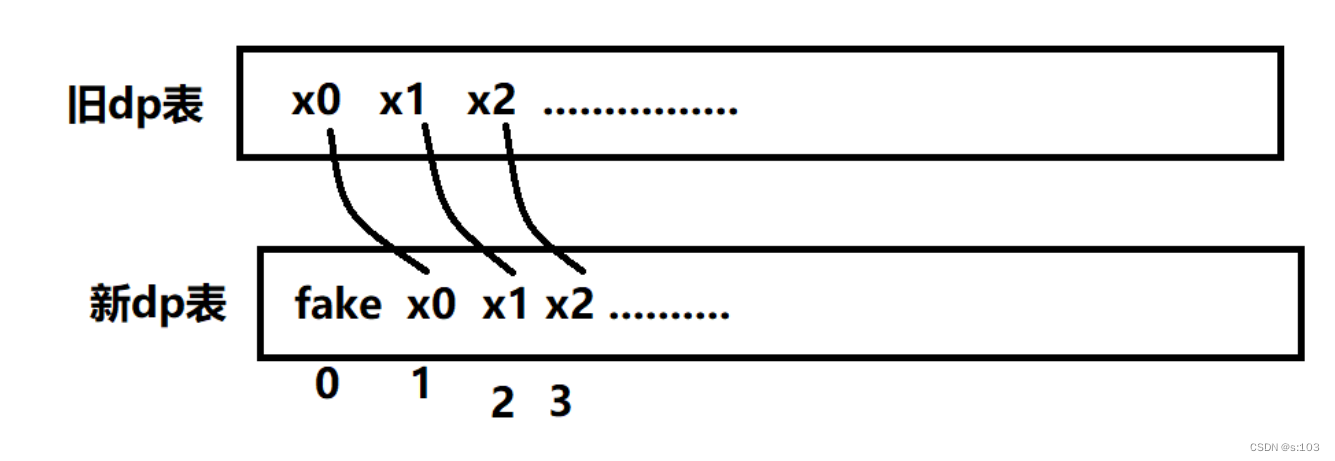
而这个fake为多少呢，一般是为0的，但是一定要据实际而言！

• 这道题fake为1才对，因为string[1]和string[2]组成功后，是一种才对，所以dp[0]=1

所以新dp表的大小为n + 1，返回值为dp[n]；

注意这里的dp[i]代表的是[0, i)的字符串子串！

class Solution {
    public int numDecodings(String s) {
        int n = s.length();

        char[] string = s.toCharArray();        
        int[] dp = new int[n + 1];
        dp[0] = 1;
        if(string[0] != '0') {
            dp[1] += 1;
        }
        if(n == 1) {
            return dp[1];
        }
        for(int i = 2; i < n + 1; i++) {
            if(string[i - 1] != '0') {
                dp[i] += dp[i - 1];
            }
            int number = (string[i - 2] - '0') * 10 + string[i - 1] - '0';
            if(number >= 10 && number <= 26) {
                dp[i] += dp[i - 2];
            }
        }
        return dp[n];
    }
}

这个小优化能掌握是更好的~

---

文章到此结束！谢谢观看
可以叫我 小马，我可能写的不好或者有错误，但是一起加油鸭🦆！

动态规划第一章结束啦，本章节讲解的类型都差不多，是不是有点“斐波那契”那味！已知推未知！牢记思想流程，特别重要

如果你理解的不错，那你很有天赋！

这动态规划的第一步走的不错！

---