"多希望有人来陪我,度过末日啊~"
讲讲我为什么突然想更新这篇栏目。
想想自己也算 "系统" 接触计算机这个学科也有差不多一年了,回想起当初下定决心要全身心投入到这个专业或者说行业中来,现在到了这样的地步,是否很符合当初对自己的期待,对这个专业行业的期待?想想做软件开发相关最最基础的四大组件,算法和数据结构、操作系统和计算机网络、数据库,再怎么说到了现在也涉略一二。对于我来说,除了在系统部分上很花时间外,其次就应当属算法,当然很多算法也会相关到部分容器,那么这类题目也会变成算法+数据结构的”双重打击”。
在第一次接触算法的时候,给我的感觉就是需要投入的时间大,以及微乎可微的反馈成果。所以一开始我对于算法其实是持有排斥的状态。可是,当你看到各个公司的笔试题,首当其冲给你甩几道面试题,而你却迟迟敲不了几行代码、捶胸敦促……痛定思痛之后,不得不重视到代码能力的提升上,其中唯一一条且至关重要的,且是一个从业者也会建议的—— “多刷刷算法题“。
道理我都懂,我也有时间有那个心气去刷,可是看到那一个个标榜“简单”难度的迟迟做不出来,一看题解似乎并没有想象的那么难,有那么点道理,开始理解,而此时评论区一片 “简单的、祥和”的画面。到一个标榜“中等”难度的题似乎成了更难以跨越的"鸿沟"更别提 那写满一张网页的“题解”……
你开始暗下决心,告诉自己“慢慢来”,你便”胸有成竹”般地给自己定下每天刷个3~4道算法题的小目标,于是乎你每天开始登上账号开始刷题,看着不会,翻翻题解,试着敲敲,似乎理解,运行成功,下一道题……而这种状态持续不了多久,你就会没了兴趣,因为你发现坚持了几天后,仍然是一事无成,竟没做出一道题!未免心里有些波动,有时候看到算法题就显得有些恐惧和排斥,那心里上暗示的每天刷题的目标,不自觉地变暗了下去,就连自己也不想再去记起……
" 多希望有人来陪我,度过末日啊~"。
还是那句话,永远不要放弃你自己,都是这么走过来的。
永恒的题解思路:
1、第N个斐波那契数
(1) 题意分析

本题肯定是非常简单的一种dp规划,因为题中就已经告知了dp的状态转移方程和初始化,没什么很大的难度。
class Solution {
public:
int tribonacci(int n) {
if(n < 1) return 0;
if(n < 2 || n < 3) return 1;
vector<int> dp(n+1);
dp[0] = 0,dp[1] = dp[2]= 1;
// 但是从T4 填dp表
for(int i=3; i <= n; ++i)
dp[i] = dp[i-1]+dp[i-2]+dp[i-3];
return dp[n];
}
};(2) 空间优化
多数时候对dp的优化要求不是那么显眼,最主要的是做出来。我们分析上述代码的时空复杂度分别为,O(n) \ O(n)。
在本题可以使用滚动数组,对空间复杂度进行优化,下降至O(1)的常数。
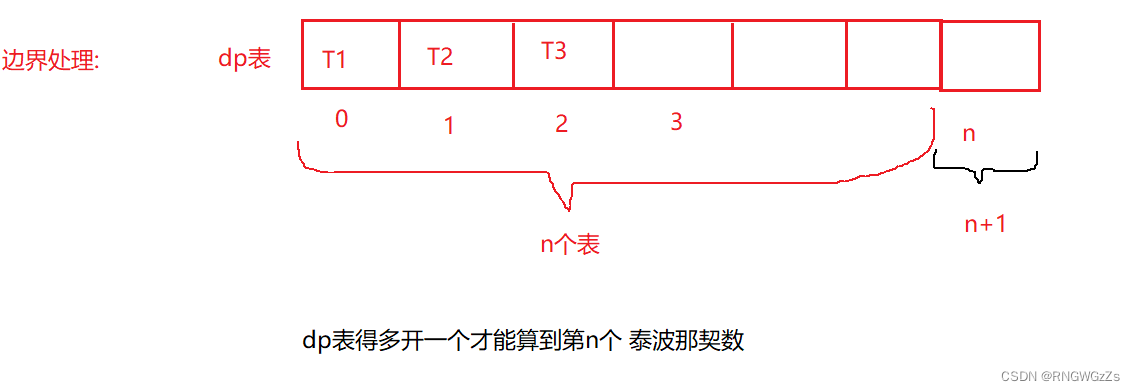
因为要求 第n个泰波那契数,本质只需要知道它前三个数的状态即可~
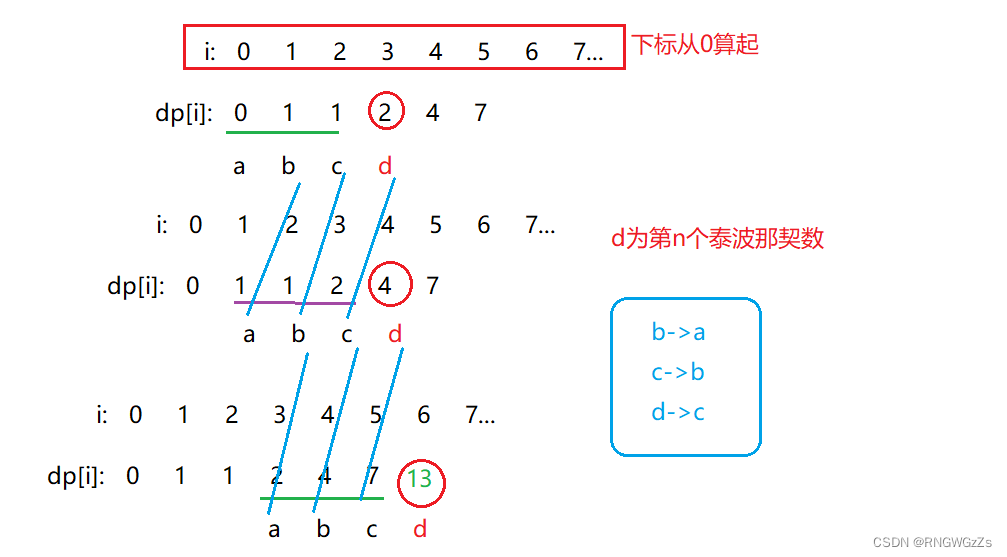
class Solution {
public:
int tribonacci(int n) {
if(n < 1) return 0;
if(n < 2 || n < 3) return 1;
int a=0;
int b=1,c=1;
int d=0;
// 这里从i下标3开始
for(int i=3; i<=n; ++i){
d = a + b + c;
// 条件更新
a = b;
b = c;
c = d;
}
return d;
}
};
2、三步问题
(1) 题目解析 
这道题桶上面那到泰波那契数,换汤不换药,仍然是根据题目得到状态表示,再根据状态表示相邻的位置,推出状态方程。
边界位置:

class Solution {
public:
int waysToStep(int n) {
if(n == 1 || n==2) return n;
if(n == 3) return 4;
// 题目要求 别忘记对加法mod
const int MOD = 1e9+7;
vector<int> dp(n+1);
dp[1] = 1,dp[2]=2,dp[3]=4;
for(int i=4; i<=n ;++i)
dp[i] = ((dp[i-1] + dp[i-2]) % MOD + dp[i-3] ) % MOD;
return dp[n];
}
};
3、最小花费爬楼梯
(1) 题目解析
思路一: 到达i位置的最小花费

边界位置:
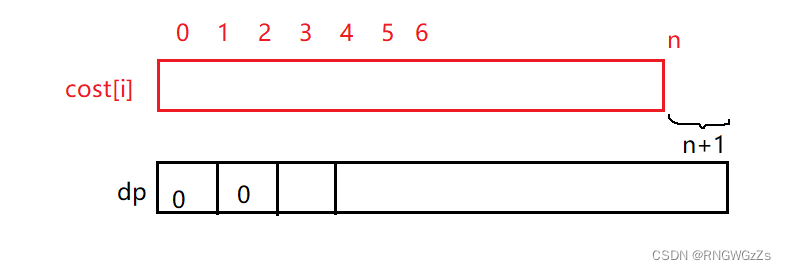
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
int n = cost.size();
vector<int> dp(n+1);
dp[0]=dp[1]=0;
for(int i=2; i<=n; ++i)
dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
return dp[n];
}
};思路二: 从i位置开始 的最小花费
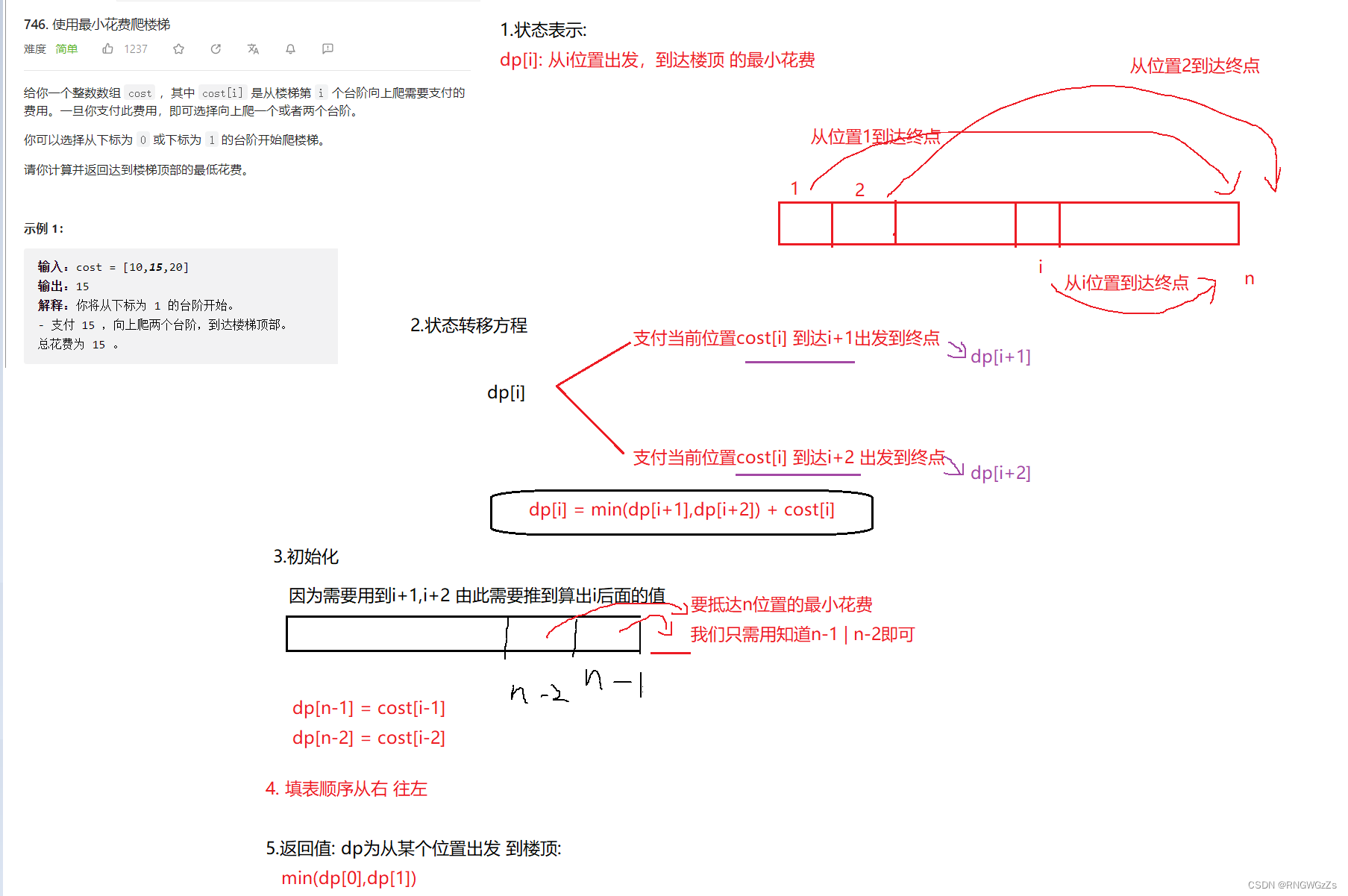
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
int n = cost.size();
vector<int> dp(n);
dp[n-1] = cost[n-1];
dp[n-2] = cost[n-2];
// 从右往左
for(int i=n-3; i>=0; --i)
// 往后
dp[i] = min(dp[i+1],dp[i+2]) + cost[i];
return min(dp[0],dp[1]);
}
};4、解码方法
(1) 题目解析

本题的核心是抓住解码的两种状态:
① 用一位进行解码,但是它有成功和失败,一旦成功那么dp[i-1]处每一个解法都可以添加一个s[i],反之一旦解码失败,说明到达第i位置处,之前的解码都是0。
② 用两位解码,也是有成功和失败,同样如果解码成功,也就意味着dp[i-2]代表的解法综总和,都可以添加上 (s[i-1],s[i] ) ,反之 为0。
class Solution {
public:
int numDecodings(string s) {
int n = s.size();
vector<int> dp(n);
dp[0] = s[0] != '0';
if(n == 1) return dp[0];
if(s[0] !='0' && s[1] !='0') dp[1] += 1;
int t=(s[0]-'0') * 10 + s[1] -'0';
if(t >= 10 && t <= 26) dp[1] += 1;
for(int i=2; i<n; ++i){
// 单独解码
if(s[i] != '0') dp[i] += dp[i-1];
// 两位解码
int t = (s[i-1]-'0') * 10 + s[i] -'0';
if(t >= 10 && t <= 26)
dp[i] += dp[i-2];
}
return dp[n-1];
}
};优化版本: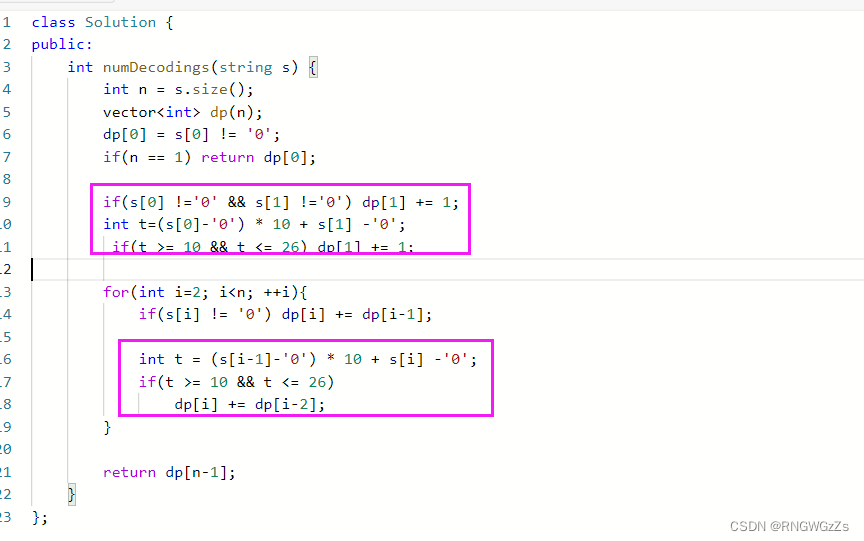
细心的你肯定能够发现,代码里标注的两处,他们的实现功能似乎是一样的,能否有个方法让代码完成复用呢? 换句话说,就是让我们把dp[2] 这个位置放到循环里面初始化。

class Solution {
public:
int numDecodings(string s) {
int n = s.size();
vector<int> dp(n+1);
dp[0] = 1;
dp[1] = s[0] != '0';
if(n == 1) return dp[1];
for(int i=2; i<=n; ++i){
// 因为dp多开了一个 对应到的s内的下标应该-1
if(s[i-1] != '0') dp[i] += dp[i-1];
int t = (s[i-2]-'0') * 10 + s[i-1] -'0';
if(t >= 10 && t <= 26)
dp[i] += dp[i-2];
}
return dp[n];
}
};
5、不同路径
(1) 题目解析
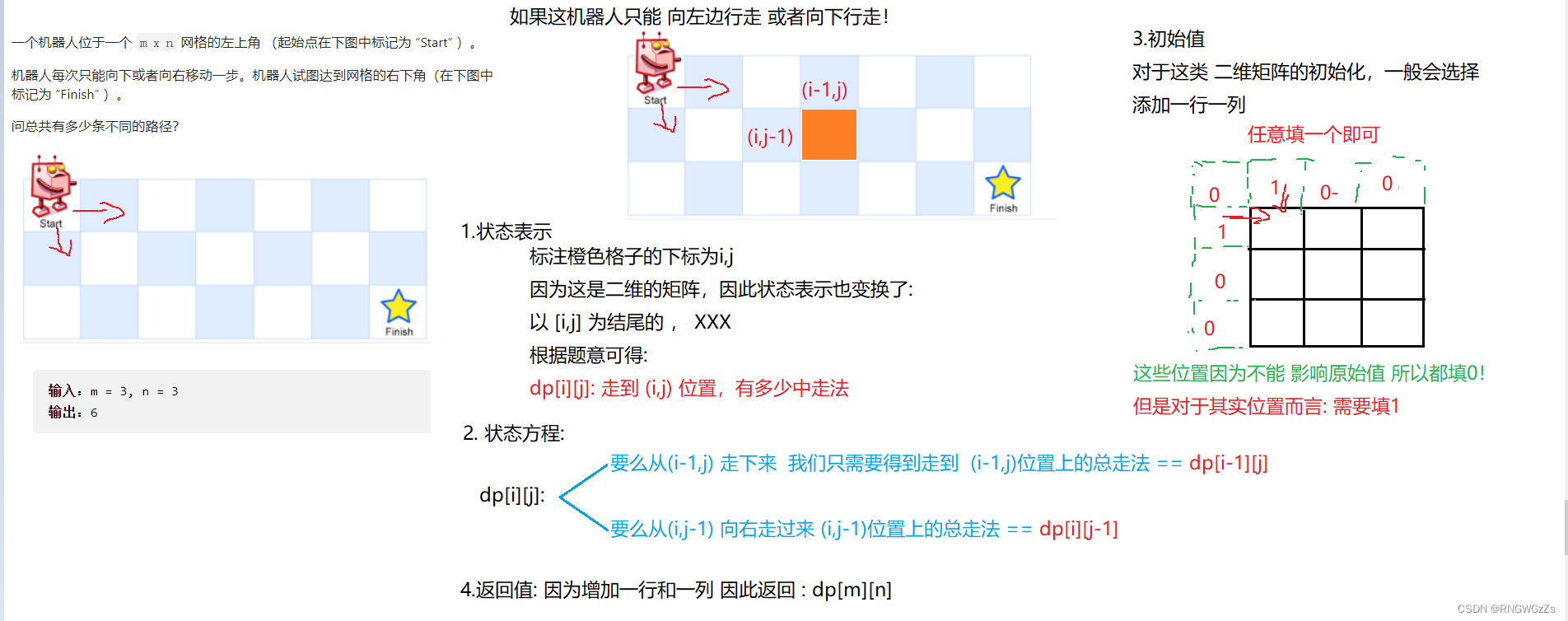
这类路径题总的来说是很简单的,找到结束位置即可。
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> dp(m+1,vector<int>(n+1));
// dp[1][0] = 1
dp[0][1] = 1;
for(int i=1; i<=m; ++i){
for(int j=1; j<=n; ++j){
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m][n];
}
};
本篇到此结束,感谢你的阅读。
祝你好运,向阳而生~