大概从下面几个部分学习：

        1.EM算法

人人都懂EM算法 - 知乎 (zhihu.com)

18分钟理解EM算法 - 知乎 (zhihu.com)

变分贝叶斯深度学习综述 - 知乎 (zhihu.com)   【未看完】

EM算法存在的意义是什么？ - 知乎 (zhihu.com)【八种境界】

EM 算法具备收敛性，但并不保证找到全局最大值，有可能找到局部最大值。

        2.指数族分布

        3.高斯混合模型

高斯混合模型（GMM） - 知乎 (zhihu.com)

多元高斯和混合高斯分布不是一回事儿，多元高斯分布是指数据在每个维度上均成高斯分布，而混合高斯分布是多个高斯模型的混合，其分模型也可以是多元的

👌🏻 高斯混合模型与EM算法的数学原理及应用实例 - 知乎 (zhihu.com)

GMM(Gaussian Mixture Model, 高斯混合模型)被誉为万能分布近似器, 其拥有强悍的数据建模能力. GMM使用若干个高斯分布的加权和作为对观测数据集进行建模的基础分布, 而由中心极限定理我们知道, 大量独立同分布的随机变量的均值在做适当标准化之后会依分布收敛于高斯分布, 这使得高斯分布具有普适性的建模能力, 继而奠定了使用高斯分布作为主要构成部件的GMM进行数据建模的理论基础. GMM是典型的概率图模型, GMM与其变种k-means(k均值)算法都是工业实践中经常使用的聚类工具. 由于GMM在建模时引入了隐变量的概念, 致使我们无法直接使用MLE(Maximum Likelihood Estimate, 极大似然估计)进行参数估计，进而引入了EM(Expectation Maximization algorithm, 最大期望算法)算法来对含有隐变量的模型进行训练. EM算法通过迭代地构造似然函数下限的方式不断地提升似然函数的取值, 从而完成对含有隐变量模型的参数估计, 其典型的应用包括GMM、HMM(Hidden Markov Model, 隐马尔可夫模型)的参数估计 

 

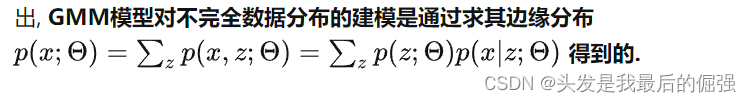
 GMM模型对不完全数据分布的建模是通过求完全数据的边缘分布求得的

        4.变分推断