SORT系列

SORT-1 项目配置运行-WINDOWS
SORT-2 卡尔曼滤波推导和示例
SORT-3 匈牙利算法和SORT类
SORT-4 SORT项目代码解析
本项目地址

SORT项目逐层详解

main

if __name__ == '__main__'
	# 设置交互模式、参数、文件路径
		|
	# 创建 SORT 对象
    mot_tracker = Sort(max_age=, min_hits=,iou_threshold) 
    	|
    # "循环"读取每一个文件（每一帧)
    for frame in range(...):
        # 参数准备
        frame += 1 	# 帧数+1
        dets[] = .. # 存放 检测框
        total_frames += 1
        	|
        # 获取检测框
        dets[] = ...
        	|
        # 用检测框 dets 做一次更新; 返回满足条件可显示的trackers([x1,y1,x2,y2,ID])
        trackers = mot_tracker.update(dets)
        	|
       	# 作画
        for d in trakcers:
            fig.canvas.flush_events()...
           

1.SORT 类

class Sort(object):
    def __init__(self, max_age=1, min_hits=3, iou_threshold=0.3):
    # Sets key parameters for SORT
    self.max_age = max_age		# tracker 的最大寿命
    self.min_hits = min_hits	# 最小匹配次数
    self.iou_threshold = iou_threshold	# 匹配阈值
    self.trackers = []        	# 存放跟踪器类 KalmanBoxTracker 对象
    self.frame_count = 0
    
    
	def update(self, dets=np.empty((0, 5))):
    # 使用 检测框 做一次更新; dets:[x1,y1,x2,y2,ID]
    	# 0.参数准备
        trks = np.zeros(len(self,trackers),5)	# 
        to_del = []			# 待删除的 预测框
        ret = []			# 可显示的 tracker
        	|
        # 1.现有的跟踪器全部做一次更新预测，获得预测框
        for t,trk in enumerate(trks):
            pos = self.trackers[t].predict()[0]      	# 已有跟踪器上做一次预测
      		trk[:]=[pos[0], pos[1], pos[2], pos[3], 0]  # 获得 "预测框" 的坐标
        	|
        	# 去除非法的预测框
        trks = np.ma.compress_rows(np.ma.masked_invalid(trks))
        	|
        	# 删除 to_del 中待删除的 tracker
        for t in reversed(to_del):
      		self.trackers.pop(t)
            |
        # 2.预测框和 检测框 做一次匹配
        matched, unmatched_dets, unmatched_trks = \
        	associate_detections_to_trackers(dets,trks, self.iou_threshold)
    		|
            
        # 3.根据匹配结果 分别更新三类 trakcer
        	# 3.1 更新匹配成功的跟踪器
        for m in matched:
             self.trackers[m[1]].update(dets[m[0], :])
    		# 3.2 为未匹配到的检测框创建一个新的跟踪器
        for i in unmatched_dets:
            trk = KalmanBoxTracker(dets[i,:])
			self.trackers.append(trk)
            |
        	# 3.3 根据跟踪器的存在时间、匹配次数等决定是否加入显示列表

1.1卡尔曼跟踪器

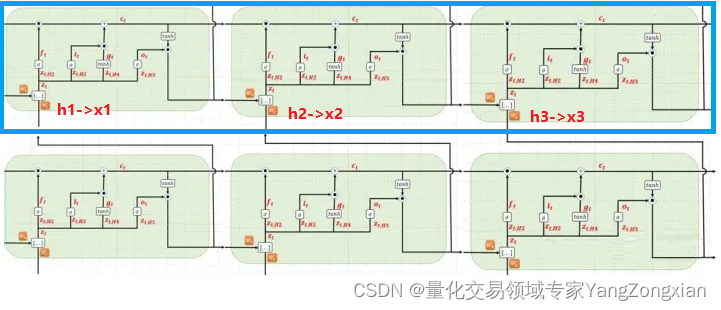
卡尔曼滤波器系统如下图所示。

输入：
状态量初始值 $x_{k-1}$和状态量协方差初始值 $P_{k-1}$
卡尔曼滤波器中的参数设置： 状态转移矩阵 $F$,映射矩阵（或称测量矩阵）$H$等
迭代输入每一步的 观测值 $Z_k$
输出：
每一步的状态预测 $x_k$

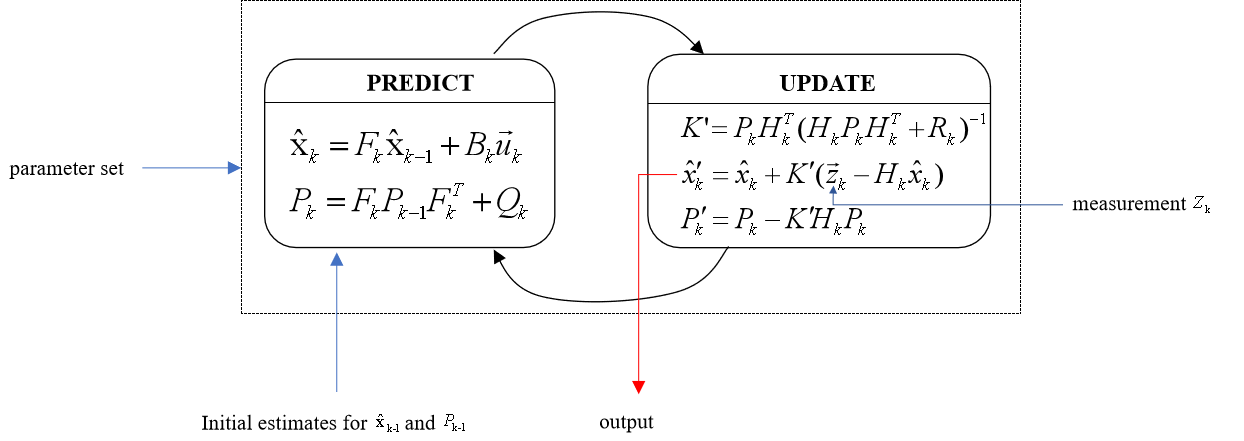
在SORT项目中，观测量 来自 YOLO 的检测结果 $bbox([x1,y1,x2,y2])$ 的转化形式 $Z([u,v,s,r])$。其中 $[u,v]$ 是中心点的坐标，$s$ 是面积，$r$ 是面积宽高比。这样四个量将是独立的变量，减弱了 bbox 四个变量之间的相关性。

由此可以定义状态量 $[x,y,s,r,\dot{x},\dot{y},\dot{s}{]}^T$，其中 $\dot{x},\dot{y},\dot{s}$ 分别是 $x,y,s$ 的一阶微分 $dx,dy,ds$。
在线性模型中，可将其视为 距离-速度 模型，即 $x_k=x_{k-1}+dxdt$，由此可得状态转移矩阵 $F$：
$F=\left[\begin{array}{c}1,0,0,0,1,0,0\\ 0,1,0,0,0,1,0\\ 0,0,1,0,0,0,1\\ 0,0,0,1,0,0,0\\ 0,0,0,0,1,0,0\\ 0,0,0,0,0,1,0\\ 0,0,0,0,0,0,1\end{array}\right]$
$x_k=F\cdot x_{k-1}=\left[\begin{array}{c}1,0,0,0,1,0,0\\ 0,1,0,0,0,1,0\\ 0,0,1,0,0,0,1\\ 0,0,0,1,0,0,0\\ 0,0,0,0,1,0,0\\ 0,0,0,0,0,1,0\\ 0,0,0,0,0,0,1\end{array}\right]\left[\begin{array}{c}x\\ y\\ s\\ r\\ \dot{x}\\ \dot{y}\\ \dot{s}\end{array}\right]$

即可得到 $x_k=x_{k-1}+\dot{x}$ ($y,s$同理)，$\dot{x}=\dot{x}$ ($r,\dot{y}$同理)。这就是卡尔曼滤波器是线性滤波器原因！

class KalmanBoxTracker(object):
    
    count = 0		# 跟踪器的存在数量,static
    
    def __init__(self,bbox):
    # 卡尔曼滤波器的主要参数设置
    self.kf = KalmanFilter(dim_x=7, dim_z=4)  # 定义状态空间和观测空间维度，解释见下
    self.kf.F = np.array([[1,0,0,0,1,0,0],[0,1,0,0,0,1,0],[0,0,1,0,0,0,1],			[0,0,0,1,0,0,0],  [0,0,0,0,1,0,0],[0,0,0,0,0,1,0],[0,0,0,0,0,0,1]])
    self.kf.H = np.array([[1,0,0,0,0,0,0],[0,1,0,0,0,0,0],[0,0,1,0,0,0,0],			[0,0,0,1,0,0,0]])

    self.kf.R[2:,2:] *= 10.
    self.kf.P[4:,4:] *= 1000. 
    self.kf.P *= 10.
    self.kf.Q[-1,-1] *= 0.01
    self.kf.Q[4:,4:] *= 0.01

    self.kf.x[:4] = convert_bbox_to_z(bbox)     # [u,v,s,r,u',v',s']
    self.time_since_update = 0
    self.id = KalmanBoxTracker.count

    KalmanBoxTracker.count += 1

    self.history = []
    self.hits = 0
    self.hit_streak = 0
    self.age = 0

    def update(self,bbox):
    # 用检测框更新 tracker（kalman filter update）
    self.time_since_update = 0  # 自第一次 update(创建) 的匹配次数
    self.history = []			# 保存历次的
    self.hits += 1
    self.hit_streak += 1        # 与检测框成功匹配的次数
    self.kf.update(convert_bbox_to_z(bbox))	# 调用库函数的 update
    
    def predict(self):
     	if((self.kf.x[6]+self.kf.x[2])<=0):
      		self.kf.x[6] *= 0.0
        
    	self.kf.predict()
    
        self.age += 1
        if(self.time_since_update>0):
          self.hit_streak = 0
        self.time_since_update += 1
        self.history.append(convert_x_to_bbox(self.kf.x))
        return self.history[-1]     # 返回最后（新）一个 bbox

1.2检测框与预测框的关联

def associate_detections_to_trackers(detections,trackers,iou_threshold = 0.3):