文章目录
- 654.最大二叉树
- 思路
- 遍历顺序
- 完整版
- 变量作用域的问题
- 修改后的完整版
- 递归进一步理解
- 关于终止条件
- 优化
- 时间复杂度和空间复杂度的优化
- 补充:二叉树的高度logn
- 617.合并二叉树
- 思路
- 完整版
- 定义新二叉树的写法
654.最大二叉树
- 本题做的时候也卡了一些问题,详见上一篇博客。同时还要注意变量的块作用域规则,很基础但是易出错
- 代码优化方面,优化方法要掌握
- 注意本题终止条件写法不同,递归数组不一定要判空
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
创建一个根节点,其值为 nums 中的最大值。
递归地在最大值 左边 的 子数组前缀上 构建左子树。
递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。

输入:nums = [3,2,1,6,0,5]
输出:[6,3,5,null,2,0,null,null,1]
解释:递归调用如下所示:
- [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。
- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。
- 空数组,无子节点。
- [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。
- 空数组,无子节点。
- 只有一个元素,所以子节点是一个值为 1 的节点。
- [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。
- 只有一个元素,所以子节点是一个值为 0 的节点。
- 空数组,无子节点。

输入:nums = [3,2,1]
输出:[3,null,2,null,1]
- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。
思路
这道题和上一道 106.中序和后序遍历构造二叉树 类似。
本题是找数组的最大值作为根节点,然后分割最大值左右两侧,将左侧分为左子树区间,右侧分为右子树区间,再在左右两侧区间内找到最大值作为左孩子和右孩子。对于左右孩子也递归地进行找最大值的操作。
遍历顺序
凡是构造二叉树类的题目,都要用前序遍历。106.中序和后序遍历构造二叉树 实际上也是前序遍历,先进行逻辑处理,再处理左右节点。构造的时候要先把根节点构造出来,再递归构造左右子树。
完整版
- 递归终止条件的考虑一般都是直接考虑递归结束逻辑+极端情况,比如本题就是nums数组是空的,106就是直接考虑数组大小是0
- root本身就是指针类型,因此nums是空的情况直接返回空指针nullptr即可
- 不能在if里面重新声明vectorleft(nums.begin(),nums.begin()+maxIndex),这样的话重新声明的left数组在if语句块之外就会被销毁。
TreeNode* contruct(vector<int>& nums){
//终止条件:数组内没有没遍历到的元素了,也就是切出来的左区间和右区间都是NULL
//也可以写成,nums数组已经空了,因为每次递归都会减去最大元素
//终止条件的考虑一般都是考虑代码运行逻辑+极端情况
if(nums.empty()){
return nullptr; //如果nums是空的,直接返回空指针
}
//找最大值及其下标
int maxValue=INT_MIN;
int index;
int maxIndex;
for(index=0;index<nums.size();index++){
if(nums[index]>maxValue){
maxValue = nums[index];//最大值
maxIndex = index;//最大值的下标
}
}
//找到最大值之后,根节点数值确定
TreeNode* root = new TreeNode(maxValue);
//分割数组
//注意:1.最大值本身要在新的数组里去掉,所以right左闭的部分应该+1
//2.不能操作空数组,maxIndex这里可能是0,是0的话就会发生操作空数组报错。但是我们的终止条件是if(nums.empty()),所以并不需要考虑操作空数组的问题
//左数组,左闭右开
vector<int>left;
//这里的写法是有问题的,在if里面重新声明了left数组,这个重新声明的数组在if语句块之外就会被销毁!
if(nums.begin()!=nums.begin()+maxIndex){
vector<int>left(nums.begin(),nums.begin()+maxIndex);
}
//右数组,左闭右开
vector<int>right;
if(nums.maxIndex+1!=nums.end()){
vector<int>right(nums.begin()+maxIndex+1,nums.end());
}
//分割数组后进行左右子树的递归,注意这里要判断left是不是空的!
root->left = contruct(left);
root->right = contruct(right);
return root;
}
变量作用域的问题
(实际上因为终止条件写的是判定空数组,因此这里根本不需要加if条件,但是变量作用域的问题也是一个bug点)
最开始的写法是:
//左数组,左闭右开
vector<int>left;
if(nums.begin()!=nums.begin()+maxIndex){
//问题就在于此处重新声明了,重新声明的left在if之外就销毁了,if之外的left并没有改变
vector<int>left(nums.begin(),nums.begin()+maxIndex);
}
//右数组,左闭右开
vector<int>right;
if(nums.maxIndex+1!=nums.end()){
vector<int>right(nums.begin()+maxIndex+1,nums.end());
}
//分割数组后进行左右子树的递归
if(!left.empty()){
root->left = contruct(left);
}
if(!right.empty()){
root->right = contruct(right);
}
但是,这样的写法存在left和right变量作用域的问题。
在C++中,变量的生命周期由其作用域决定。在if语句块(以及所有其他类型的块,例如while、for循环和自定义块)中声明的变量只在该块内部有效。一旦代码执行离开了该块,块内声明的所有变量都将被销毁。
因此,在 if 语句内部创建 left 和 right 向量,然而这样创建的向量只在 if 语句块内有效,出了 if 语句块,这些向量就会被销毁,就会导致:
//分割数组后进行左右子树的递归
root->left = contruct(left);
root->right = contruct(right);
这一部分的递归,找不到 left 和 right 数组,因为这两个数组已经在if语句块中被销毁。
**这种规则不仅适用于if语句块,而且适用于所有的代码块。这是一种被称为“块作用域”的规则。这就是说,一旦你在一个块中(用大括号 { } 定义的代码区域)声明了一个变量,那么这个变量只在该块及其子块中存在。**出了这个块,这个变量就不存在了。
这种规则有助于管理内存和避免变量名冲突。对于更大的程序,正确管理变量的作用域是非常重要的,可以避免很多错误。
应该修改为:
//左数组,左闭右开
vector<int>left;
if(nums.begin()!=nums.begin()+maxIndex){
left = vector<int>(nums.begin(),nums.begin()+maxIndex);
}
//右数组,左闭右开
vector<int>right;
if(nums.maxIndex+1!=nums.end()){
right = vector<int>(nums.begin()+maxIndex+1,nums.end());
}
修改也要注意left和right的赋值方式,if里面绝对不能重新声明vectorleft = (),这样的话left的值仍然是出了if语句块就会被销毁。
如果像最开始的写法一样,在 if 语句内部重新声明 vector<int> left,这将会创建一个新的 left 向量,这个新的向量仅在 if 语句块的作用域内有效,在 if 语句块外部,原来的 left 向量并没有被改变。
修改后的完整版
class Solution {
public:
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
//终止条件:数组内没有没遍历到的元素了,也就是切出来的左区间和右区间都是NULL
//条件是if(nums.empty())的话,就不需要判断left和right是不是空的,是否存在操作空数组的问题了。
if(nums.empty()){
return nullptr; //返回空指针
}
//找最大值及其下标
int maxValue=INT_MIN;
int index;
int maxIndex;
for(index=0;index<nums.size();index++){
if(nums[index]>maxValue){
maxValue = nums[index];//最大值
maxIndex = index;//最大值的下标
}
}
//找到最大值之后,根节点数值确定
TreeNode* root = new TreeNode(maxValue);
//nums.erase(nums[maxIndex]);
//分割数组
//左数组,左闭右开
vector<int>left = vector<int>(nums.begin(),nums.begin()+maxIndex);
//分割数组后进行左右子树的递归
//这种写法不需要判断是不是操作空数组left,因为终止条件会判定
root->left = constructMaximumBinaryTree(left);
//右数组,左闭右开
vector<int>right = vector<int>(nums.begin()+maxIndex+1,nums.end());
root->right = constructMaximumBinaryTree(right);
return root;
}
};
递归进一步理解
当我们在递归调用 constructMaximumBinaryTree(left)时,新的 left 数组会传递给 constructMaximumBinaryTree 函数作为它的 nums 参数,并代替nums执行nums的所有操作。
也就是说,发生递归的时候,当我们传入constructMaximumBinaryTree(left)的时候,函数最开始的if(nums.empty()) 判断,nums会自动换成left。递归函数会对这个新的 nums 数组执行与前一次递归调用相同的操作。
这就是递归的本质——你在调用同一个函数,但每次调用时传递的参数可能不同,然后这个函数会对传递进来的参数执行相同的操作。
关于终止条件
因为这道题力扣上的要求里,写了nums不为空,因此本题终止条件实际上也可以写成
if(nums.size()==1){
return root(nums[0]);//直接构造根节点返回
}
但是,这种写法,在递归传入left之前,必须先判断left是不是空,否则就会涉及到操作空数组的问题,因为这种终止条件写法,并没有在最前面判空并返回的操作。就会涉及到操作空数组问题。空数组报错问题详见上一篇博客。(1条消息) Char 45: runtime error: applying non-zero offset 131060 to null pointer (stl_iterator. h)_大磕学家ZYX的博客-CSDN博客
优化
这种写法还是比较冗余的,并且效率很低。为什么效率低,因为每次分割nums数组的时候,都构造了一个新数组。构造新数组本来就是很耗时的。
代码的优化就是不构造新数组,直接在原有数组nums的基础上进行切割,也就是直接操作下标。每次传入参数的时候,直接传入nums里面左右区间的下标就可以了!
优化写法如下:
- 由于优化之后的写法,在传入nums数组的同时还要传入左区间和右区间,因此需要单独把函数拿出来,以便于修改增加函数参数
class Solution {
private:
// 在左闭右开区间[left, right),构造二叉树
TreeNode* traversal(vector<int>& nums, int left, int right) {
if (left >= right) return nullptr;
// 分割点下标:maxValueIndex
int maxValueIndex = left;
for (int i = left + 1; i < right; ++i) {
if (nums[i] > nums[maxValueIndex]) maxValueIndex = i;
}
TreeNode* root = new TreeNode(nums[maxValueIndex]);
// 左闭右开:[left, maxValueIndex)
root->left = traversal(nums, left, maxValueIndex);
// 左闭右开:[maxValueIndex + 1, right)
root->right = traversal(nums, maxValueIndex + 1, right);
return root;
}
public:
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
return traversal(nums, 0, nums.size());
}
};
时间复杂度和空间复杂度的优化
-
空间复杂度:该方法不再创建新的数组副本,而是通过传递下标,直接在原数组上进行操作,大大减少了空间的使用。这种优化使得空间复杂度从O(nlogn)降低到了O(n),其中n为数组长度。这在数组非常大的情况下会有显著的性能提升。
原空间复杂度是O(nlogn)是因为每一层递归都要创建新数组,当树元素数目是n的时候,树的高度是
logn。 -
时间复杂度:虽然该方法并没有显著地降低时间复杂度,但由于避免了新数组的创建和删除,减少了大量的内存操作,因此在实际运行时,可能会比创建新数组的版本快一些。
总的来说,这种写法的主要优化在于空间复杂度的降低和内存操作的减少,这使得算法更加高效。但是,无论采用哪种方式,时间复杂度的主要部分仍然来自于查找最大值,这部分的时间复杂度为O(n),所以总体的时间复杂度仍然是O(n^2),其中n为数组长度。
补充:二叉树的高度logn
对于一个完全平衡的二叉树(每个节点的左右子树的高度差不超过1),如果树有n个节点,那么它的高度大约是log(n)。这是因为每增加一层,节点的数量大约会翻倍。对于这样的二叉树,任何一个节点(代表数组中的一个元素)都在从根到叶子的路径上,而这条路径的长度就是树的高度,大约是log(n)。
原先的做法,每次递归都需要创建新的数组,这样每个元素最多会被复制 log(n) 次(在平衡树的情况下),所以空间复杂度是 O(nlogn)。
而在优化后的做法中,由于我们直接在原数组上进行操作,并没有创建新的数组,因此避免了数组的复制。这种情况下,主要的空间消耗来自于递归调用的栈空间。在最坏的情况下(即树退化为链表,递归深度达到 n),空间复杂度是 O(n)。在最好的情况下(即树完全平衡,递归深度为 log(n)),空间复杂度是 O(logn)。
617.合并二叉树
给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
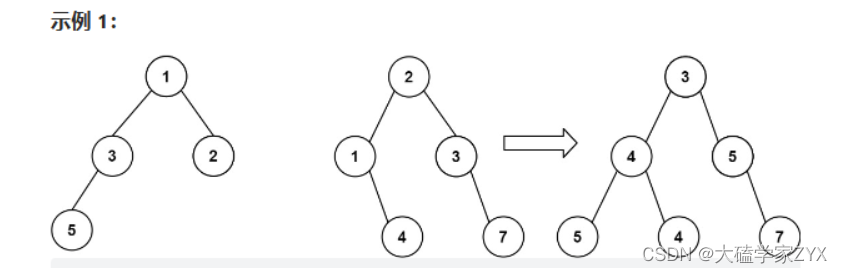
输入:root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出:[3,4,5,5,4,null,7]
示例 2:
输入:root1 = [1], root2 = [1,2]
输出:[2,2]
思路
这道题比较难的点在于一起操作两个二叉树。遍历顺序方面,因为也是构造一棵新的二叉树,所以选择前序遍历。前序遍历中左右,先合并根节点,再处理左右节点。
完整版
- 这种写法为降低空间复杂度,直接改tree1
TreeNode* mergeTrees(TreeNode* root1,TreeNode* root2){
//终止条件
//如果tree1这个节点是空的,就返回tree2对应位置的节点
if(root1==NULL){
return root2; //tree1和tree2的遍历逻辑是同步进行遍历,终止条件可以先写上
}
if(root2==NULL){
return root1; //这里如果tree1和tree2同时为空,就是直接return NULL,并不影响,已经包含了
}
//单层递归,前序遍历
//降低空间复杂度,我们直接改tree1,不重新定义
//两个节点都存在
root1->val+=root2->val;
root1->left = mergeTrees(root1->left,root2->left);
root1->right = mergeTrees(root1->right,root2->right);
return root1;
}
定义新二叉树的写法
- 如果tree1和tree2不能修改,我们就定义新的二叉树来存放合并结果
TreeNode* mergeTrees(TreeNode* root1,TreeNode* root2){
//终止条件不变
//如果tree1这个节点是空的,就返回tree2对应位置的节点
if(root1==NULL){
return root2; //tree1和tree2的遍历逻辑是同步进行遍历,终止条件可以先写上
}
if(root2==NULL){
return root1; //这里如果tree1和tree2同时为空,就是直接return NULL,并不影响,已经包含了
}
//单层递归,前序遍历
//定义新的树节点
TreeNode* newTree = new TreeNode;
newTree->val = root1->val+root2->val;
newTree->left = mergeTrees(root1->left,root2->left);
newTree->right = mergeTrees(root1->right,root2->right);
return newTree;
}
此时开辟了新的空间,空间复杂度是O(n),n是合并后新二叉树的节点个数。
101.对称二叉树 实际上也是操作两个二叉树,对称二叉树是对比根节点左子树和右子树是否可以相互翻转。可以结合本题一起来看。