二叉树的层序遍历以及队列的实现

news2024/11/16 4:25:41

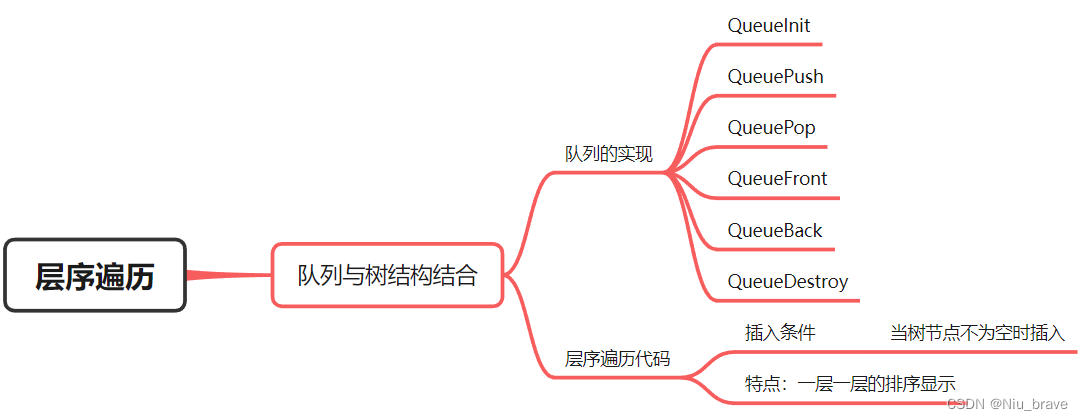
思维导图：

一，什么是层序遍历

层序遍历，顾名思义就是一层一层的遍历。比如我的这棵二叉树：

如果使用层序遍历的话它的结果就会是这样的：

1->5->9->7->10->13->8,这就是一层一层的遍历，一层一层的打印节点的值。

这个遍历方法与前面我介绍过的二叉树里面的其它方法都不一样，因为这是一个非递归的遍历方法。层序遍历的实现还要与另一种数据结构——栈结合在一起实现。

二，队列的实现

1.队列的结构

栈的结构可能是现在我们学过的比较复杂的一个结构，因为它是一个双层嵌套的结构。

代码：

typedef struct BTreeNode* QnodeData;
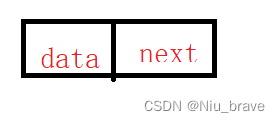
typedef struct Qnode {//队列中的某一个节点的结构
	QnodeData data;//节点值
	struct Qnode* next;//节点指针
}Qnode;

typedef struct Queue//整个队列的结构
{
	Qnode* phead;//头
	Qnode* ptail;//尾
	int size;//长度
}Queue;

一个节点：

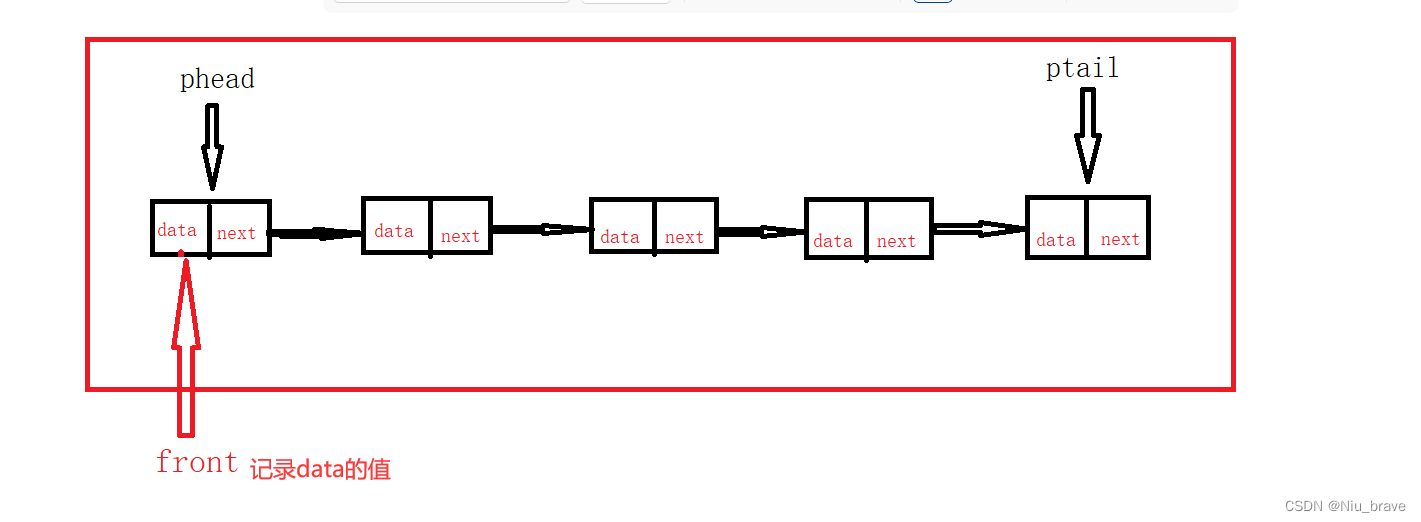
多个节点：

队列的结构大概就是这样的，就像一个链表的结构。

2.初始化

队列的初始化就是要将队列的模型给刻画出来，我们一般会将指针的指向初始化为NULL,int型变量初始化为0。所以我们便可以写出如下代码。

代码：

void QueueInit(Queue* pq )
{
	assert(pq);
	pq->phead = NULL;
	pq->ptail = NULL;
	pq->size = 0;
}

3.插入

队列的插入操作与链表的插入操作不会有太多的区别，基本上都是一样的。主要需要注意一个地方就是当这个节点是空节点的时候需要将phead与ptail指向同一个节点。

void QueuePush(Queue* pq)
{
	assert(pq);
	Qnode* newnode = (Qnode*)malloc(sizeof(Qnode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		return;
	}
	if (pq->phead == NULL)//当节点为空时的处理方法
	{
		assert(pq->ptail == NULL);
		pq->phead = pq->ptail = newnode;
	}
	else 
	{
		pq->ptail->next = newnode;
		pq->ptail = newnode;
	}
	pq->size++;//插入一个节点时就要将长度增加
}

4.弹出元素

因为队列的特点是先进先出所以队列的弹出操作是固定的，不存在头删与尾删的选择。它只能够实现头删，而不存在尾删。所以根据这个逻辑我们实现的代码如下。

代码：

void QueuePop(Queue* pq)
{
	assert(pq);//pq不能为空
	assert(pq->ptail!=NULL);//队列不能为空
	Queue* next = pq->phead->next;
	free(pq->phead);
	pq->phead = next;
    if(pq->phead == NULL)
     {
       pq->phead == NULL;//当头指针指向NULL时就要将pq->ptail也置为NULL
      }
	pq->size--;
}

其实这里还有可以改进的地方，比如说：
assert(pq);//pq不能为空
assert(pq->ptail!=NULL);//队列不能为空
这两个assert就会比较让人混淆，所以我们可以将第二个断言这样实现。

先写一个判空的函数：
bool isEmpty(Queue* pq)
{
	return pq->ptail == NULL
		&& pq->phead == NULL;//当两者为空时返回true来达到判空的作用
}
说以第二个断言就改成：
assert(！isEmpty(pq));//队列不能为空

这样的断言就清晰一点了。

5.获取头元素与尾元素以及长度。

这两个操作算是最简单的操作了，所以在这里就不再多说了。

代码：

Qnode* QueueFront(Queue* pq)//前
{
	assert(pq);
	return pq->phead;
}
Qnode* QueueBack(Queue* pq)//后
{
	assert(pq);
	return pq->ptail;
}
int QueueSize(Queue* pq)//长度
{
	assert(pq);
	return pq->size;
}

6.销毁队列

这个对列看起来其实就是一个单链表的结构，所以销毁队列的操作也是像销毁单链表一样，也是一个一个节点这样子销毁释放。所以，按照销毁单链表的逻辑来写的代码就是如下代码：

代码：

void QueueDestory(Queue* pq)
{
	assert(pq);
	while (pq->phead)
	{
		Qnode* next = pq->phead->next;//记录下一个节点的值
		free(pq->phead);//销毁当前节点
		pq->phead = next;
	}
	pq->phead = pq->ptail = NULL;//销毁完以后将头尾节点置为NULL
}

三，层序遍历的实现

层序遍历就像前面所说的那样，它就是一层一层的来遍历显示的。这个遍历方法不是递归的而是非递归的，所以想要实现这个遍历就得用栈的先进先出的特点来实现。为了更好的讲解我先将代码写上：
void LevelOrder(BTreeNode* root)
{
	Queue pq;//创造一个队列
	QueueInit(&pq);//初始化队列
	
	QueuePush(&pq, root);//先将一个根节点插入到队列中
	
	while (!isEmpty(&pq))
	{
		BTreeNode* front = QueueFront(&pq);//接收队列中第一个元素
		printf("%d->", front->val);
		QueuePop(&pq);//将第一个元素清出队列

		if (front->left)
			QueuePush(&pq, front->left);//插入左节点
		if (front->right)
			QueuePush(&pq, front->right);//插入右节点
	}
	QueueDestory(&pq);//销毁队列
} 
在这个层序遍历的代码中，值得研究的点有很多比如QueueFront这个函数。

QueueFront函数代码：
Qnode* QueueFront(Queue* pq)
{
	assert(pq);
	return pq->phead->data;

}
data的类型：树节点的指针
typedef struct BtreeNode* DataType;
为什么这里的data要使用节点的指针的类型呢？这是因为我需要找到接下来的左节点与右节点。只有在知道了树节点的地址以后才能找到当前节点的左右节点

再比如这一段代码：
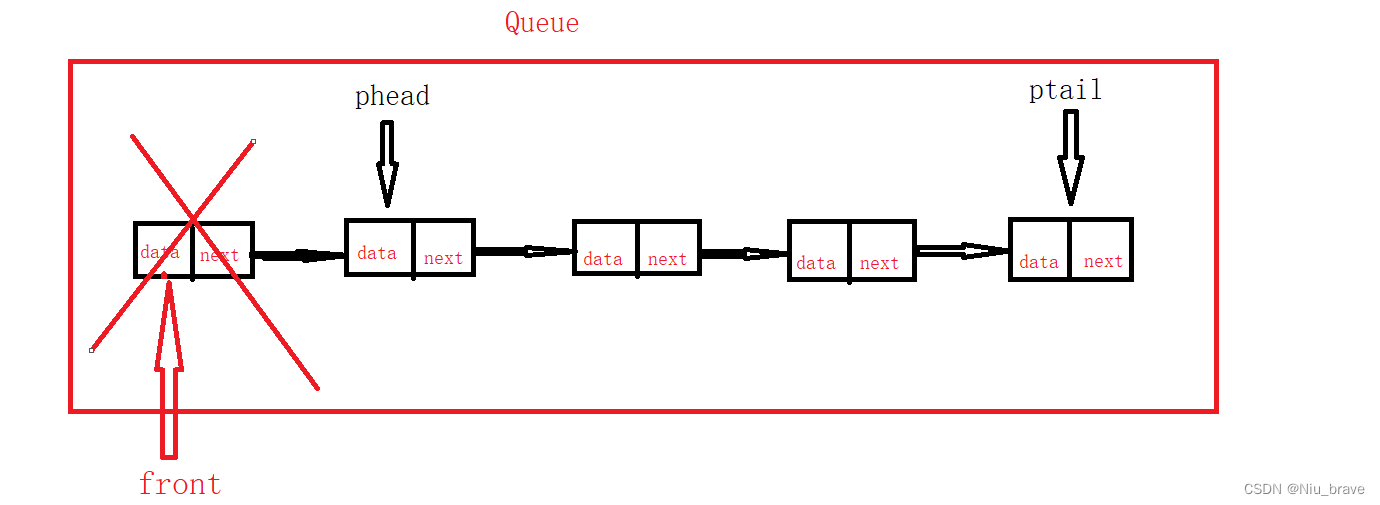
BTreeNode* front = QueueFront(&pq);//接收队列中第一个元素
		printf("%d->", front->val);
		QueuePop(&pq);//将第一个元素清出队
可能会有人疑惑为什么在我们pop以后front还没有变成一个野指针。现在来画图看看Queue的结构：

在执行pop操作的时候这个图就会变成这样：

pop这个操作只是将队列的头节点删除了而对这个front指针其实没有什么影响，因为front指向的是一个地址这个地址是树节点的地址树节点没有被销毁，所以这个地址仍然有效。