【LeetCode】每日一题 -- 1171. 从链表中删去总和值为零的连续节点 -- Java Version

news2024/11/17 5:51:21

题目链接：https://leetcode.cn/problems/remove-zero-sum-consecutive-nodes-from-linked-list/

1. 题解（1171. 从链表中删去总和值为零的连续节点）

2021年字节二面真题

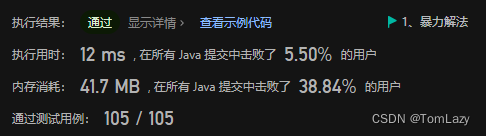
1.1 暴力解法：穷举

时间复杂度 O(n²)，空间复杂度O(1)

【解题思路】：
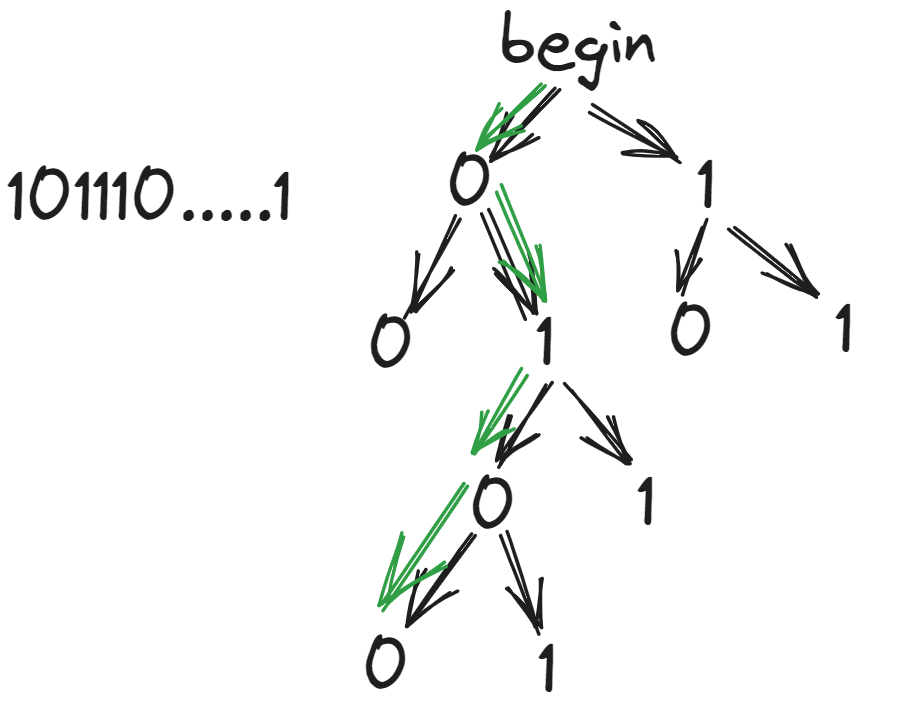
由题意得，题目中要我们删除的是总和值为 0 的连续节点组成的序列，这句话的重点有两个：

总和为0；
连续；

……
明白了这两点，我们很容易想出该题的暴力解法：从头开始，对每个节点都向后遍历一次，找出遍历过程中导致总和为0的节点，然后让该节点的前一节点指向恰好导致总和为0的节点的后一节点，完成删除操作。
PS：定义哨兵节点的原因，就是防止头节点也有可能会被删除（需要前一节点）。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode removeZeroSumSublists(ListNode head) {
        ListNode sentinel = new ListNode(Integer.MAX_VALUE,head);
        ListNode cur = sentinel.next;
        ListNode pre = sentinel;

        while(cur != null) 
        {
            ListNode node = cur;
            int sum = 0;
            while (node != null) 
            {
                sum += node.val;
                node = node.next;
                if (sum == 0) 
                {
                    pre.next = node;
                    //break;
                }
            }
            pre = cur;
            cur = cur.next;
        }

        return sentinel.next;
    }
}

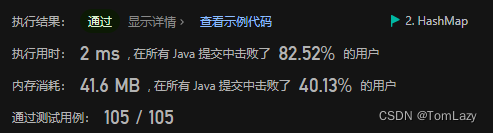
在这里插入图片描述

1.2 精简解法：HashMap ⭐

时间复杂度O(n)，空间复杂度O(n)

【解题思路】：
使用HashMap实现类似前缀和的思想，分为两次遍历：

第一次遍历，将达到当前节点时的总和 sum 和当前节点一起存入 map；
第二次遍历，借助了HashMap的特性，如果出现了重复的key，那么后一个键值对就会覆盖掉前一个，因此，当我们再次遍历时，如果链表中真的存在总和值为 0 的连续节点组成的序列，那么我们此时通过map.get(sum)找到的就是这个连续序列的最后一个节点，那么我们就可以让当前节点的next指向map.get(sum).next，完成删除序列。

class Solution {
    public ListNode removeZeroSumSublists(ListNode head) {
        ListNode sentinel = new ListNode(0,head);
        HashMap<Integer, ListNode> map = new HashMap<>();

        // 首次遍历建立 节点处链表和<->节点 哈希表
        // 若同一和出现多次会覆盖，即记录该sum出现的最后一次节点
        int sum = 0;
        for (ListNode cur = sentinel; cur != null; cur = cur.next) 
        {
            sum += cur.val;
            map.put(sum, cur);
        }

         // 第二遍遍历 若当前节点处sum在下一处出现了则表明两结点之间所有节点和为0 直接删除区间所有节点
        sum = 0;
        for (ListNode cur = sentinel; cur != null; cur = cur.next)
        {
            sum += cur.val;
            cur.next = map.get(sum).next;
        }

        return sentinel.next;
    }
}