动态规划

1. 背包

1. 1024. 装箱问题

题意：有一个箱子容量为 V，同时有 n 个物品，每个物品有一个体积（正整数）。要求 n 个物品中，任取若干个装入箱内，使箱子的剩余空间为最小。
别学那么死板。换种说法，每个物品体积是v，价值是v，此时的f[V]表示的就是体积不超过V的情况下，体积的最大值。然后答案就是 $V - f [V]$

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = 35, maxv = 20010;
int f[maxv], v[maxn], V, N;
int main() {
	scanf("%d%d", &V, &N);
	for (int i = 1; i <= N; i++) {
		scanf("%d", &v[i]);
	}
	for (int i = 1; i <= N; i++) {
		for (int j = V; j >= v[i]; j--) {
			f[j] = max(f[j], f[j - v[i]] + v[i]);
		}
	}
	printf("%d\n", V - f[V]);
	return 0;
}

2. 734. 能量石

题意：吃完第 $i$ 块能量石需要花费的时间为 $S_i$ 秒。第 $i$ 块能量石最初包含 $E_i$ 单位的能量，并且每秒将失去 $L_i$ 单位的能量。能量石中包含的能量最多降低至 $0$ 。请问杜达通过吃能量石可以获得的最大能量是多少？
贪心思路：吃第 $i$ 块儿石头和第 $i + 1$ 块儿石头顺序的区别： $E_i' + E_{i+1}'-S_i*L_{i+1}$ 和 $E_i' + E_{i+1}'-S_{i+1}*L_{i}$ . 则 $\frac{S_i}{E_i}$ 越小，获得的能量越多。不过在结构体里面重载函数时，可以写成 $S_i*L_{i+1}<L_{i+1}*S_i$ .
按照上述排完序之后，然后设 $f (i, j)$ 为从前 $i$ 个物品中选，且总体积恰好是 $j$ 的方案的能量最大值。则 $f(i, j) = \max\{f(i - 1, j), f(i - 1, j - s) + e - (j - s) * l\}$ . 不过不用管能量是否减到负数。因为这种情况会被不选这种物品的方案替代掉.
zzh认为：正常的背包问题，物品价值不随时间改变，也就是说选择的顺序不影响答案。但是这个题选择的顺序会影响答案，因此找到一组可行的选择组合时，要按照贪心的性质进行选择，保证顺序是最优的. 当然这个题还有一个性质，就是能量石的能量不会降到负数，因此需要dp. 如果可以是负数的话，那么排完序之后按照顺序从前到后选择即可.

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxv = 10010, maxn = 110, V = 10000;
int f[maxv], N, kase;
struct P{
	int e, s, l;
	bool operator<(const P& rhp)const {
		return s * rhp.l < l* rhp.s;
	}
}G[maxn];
int main() {
	int T;
	scanf("%d", &T);
	while (T--) {
		scanf("%d", &N);
		memset(f, -0x3f, sizeof f);
		f[0] = 0;
		for (int i = 0; i < N; i++) {
			scanf("%d%d%d", &G[i].s, &G[i].e, &G[i].l);
		}
		sort(G, G + N);
		for (int i = 0; i < N; i++) {
			int s = G[i].s, e = G[i].e, l = G[i].l;
			for (int j = V; j >= s; j--) {
				f[j] = max(f[j], f[j - s] + e - (j - s) * l);
			}
		}
		int ans = 0;
		for (int i = 0; i <= V; i++) ans = max(f[i], ans);
		printf("Case #%d: %d\n", ++kase, ans);
	}
	return 0;
}

3. Coins

题意：给定 $n$ 种硬币，其中第 $i$ 种硬币的面值为 $A_i$ ，共有 $C_i$ 个. 问 $\sim M$ 之间能被凑成的面值有多少个？ $\le n \le 100,1 \le m \le 10^5,1\le A_i \le 10^5,1 \le C_i \le 1000$ .
设 $u s d [j]$ 表示 $f [j]$ 在选择第 $i$ 种硬币的时候，需要的最少硬币数。那么在 $f [j - a [i]]$ 已经为 $t r u e$ 的时候，如果 $f [j]$ 为 $t r u e$ ，就不进行状态转移，并令 $u se d [j] = 0$ . 如果 $f [j]$ 为 $f a l se$ ，就进行 $u se d [j] = u se d [j - a [i]] + 1$ 的转移.

#include<bits/stdc++.h>
using namespace std;
const int N = 110, M = 100010;
bitset<M> f;
int used[M], a[N], c[N];
int n, m;
int main()
{
    while(cin >> n >> m, n)
    {
        f.reset();
        f[0] = 1;
        for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
        for(int i = 1; i <= n; i++) scanf("%d", &c[i]);
        for(int i = 1; i <= n; i++)
        {
            fill(used + 1, used + m + 1, 0);
            for(int j = a[i]; j <= m; j++)
            {
                if(!f[j] && f[j - a[i]] && used[j - a[i]] < c[i])
                {
                    f[j] = 1, used[j] = used[j - a[i]] + 1;
                }
            }
        }
        //把0扣掉
        int ans = f.count() - 1;
        printf("%d\n", ans);
    }
}

4. 1013. 机器分配

题意：把 $M$ 台机器分配给 $N$ 个公司，给一个 $N * M$ 的矩阵， $w (i, j)$ 表示第 $i$ 个公司分配 $j$ 台机器的盈利。求最大收益与方案。
机器数量是背包容量，每个公司是一组物品，每组物品只能选一个。

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = 20;
int w[maxn][maxn], f[maxn][maxn], N, M, ans[maxn];
int main() {
	scanf("%d%d", &N, &M);
	for (int i = 1; i <= N; i++) {
		for (int j = 1; j <= M; j++) {
			scanf("%d", &w[i][j]);
		}
	}
	for (int i = 1; i <= N; i++) {
		for (int j = 0; j <= M; j++) {
			f[i][j] = f[i - 1][j];
			for (int k = 1; k <= j; k++) {
				f[i][j] = max(f[i][j], f[i - 1][j - k] + w[i][k]);
			}
		}
	}
	int j = M;
	for (int i = N; i >= 1; i--) {
		for (int k = 0; k <= M; k++) {
			if (j >= k && f[i][j] == f[i - 1][j - k] + w[i][k]) {
				ans[i] = k;
				j -= k;
				break;
			}
		}
	}
	printf("%d\n", f[N][M]);
	for (int i = 1; i <= N; i++) {
		printf("%d %d\n", i, ans[i]);
	}
	return 0;
}

5. 487. 金明的预算方案

题意：每个主件可以有0个、1个或2个附件（如果想买附件必须先买主件）。他希望在不超过V元的前提下，使每件物品的价格与重要度的乘积的总和最大。
思路不难，代码确实不是很好设计。看看y总怎么用二进制枚举的。

#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;
const int maxv = 32010, maxn = 70;
typedef pair<int, int> P;
P master[maxn];
vector<P> servent[maxn];
int f[maxv], N, V;
int main() {
	scanf("%d%d", &V, &N);
	for (int i = 1; i <= N; i++) {
		int v, p, q;
		scanf("%d%d%d", &v, &p, &q);
		if (!q) master[i] = { v, v * p };
		else servent[q].push_back({ v, v * p });
	}

	for (int i = 1; i <= N; i++) {
		if (!master[i].first) continue;
		for (int j = V; j >= 0; j--) {
			auto& sv = servent[i];
			for (int k = 0; k < 1 << sv.size(); k++) {
				int v = master[i].first, w = master[i].second;
				for (int u = 0; u < sv.size(); u++) {
					if (k >> u & 1) {
						v += sv[u].first;
						w += sv[u].second;
					}
				}
				if (j >= v) f[j] = max(f[j], f[j - v] + w);
			}
		}
	}
	printf("%d\n", f[V]);
	return 0;
}

2. 组合计数

1. 532. 货币系统

在网友的国度中共有 $n$ 种不同面额的货币，第 $i$ 种货币的面额为 $a [i]$ ，你可以假设每一种货币都有无穷多张。为了方便，我们把货币种数为 $n$ 、面额数组为 $a [1.. n]$ 的货币系统记作 $(n, a)$ 。找到一个 $(m, b)$ 与 $(n, a)$ 等价，且 $m$ 最小。那么有如下性质：

${b\}$ 一定可以把 ${a\}$ 中的每一个数都表示出来。
$b_i$ 一定是从 ${a\}$ 中选出来的。
$b_i$ 一定不能从 ${b\}$ 中的其他数字表示出来。
用方案数就可以判断出来， $f(a_i)=1$ 时，就是不能被其他 $a_i$ 表示出来的，那就必须要选择了。

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxv = 25010, maxn = 110;
int a[maxn], f[maxv], V, N;
int main() {
	int T;
	scanf("%d", &T);
	while (T--) {
		V = 0;
		memset(f, 0, sizeof f);
		f[0] = 1;
		scanf("%d", &N);
		for (int i = 1; i <= N; i++) {
			scanf("%d", &a[i]);
			V = max(V, a[i]);			
		}
		for (int i = 1; i <= N; i++) {
			for (int j = a[i]; j <= V; j++) {
				f[j] += f[j - a[i]];
			}
		}
		int ans = 0;
		for (int i = 1; i <= N; i++) {
			ans += (f[a[i]] == 1);
		}
		printf("%d\n", ans);
	}
	return 0;
}

2. C. On the Bench

设集合 A 有 $n_1$ 个 $a_1$ , $n_2$ 个 $a_2$ ,…, $n_m$ 个 $a_m$ 问使其相邻两个数不相同的排列有多少种.

多重集合交错排列
如果把这 n 个数分块，块的内部都是同一组的数字，并且分块儿的过程忽视掉快与块之间的顺序，相当于集合的概念。那么，按照容斥原理，答案应该是：n块的排列，减去n-1块的排列（有连续的两个数字是同一组，而在算dp的过程中，dp[n-1] 已经包含了这个情况的所有方案）……然后就是这样的容斥原理。 $ans=dp[n]n!−dp[n−1](n−1)!+⋯+(−1)^{(n−i)}dp[i]i!+...-dp[1]*1! + dp[0]*0!$
设 $d p [i] [k]$ 表示考虑前 i 种数分成 k 块的个数，那么，
$dp[i][k]=∑_{j=1}^kdp[i−1][k−j]C_{n_i−1}^{j−1}∗\frac{n_i!}{j!}$
- $d p [0] [0] = 1.$
- 因为不考虑块与块之间的顺序，所以可以看作前 $k - j$ 个块放在前面，然后把后面的第 $i$ 组数字分成 $j$ 组，就是隔板法+排列 $n_i!C_{n_i-1}^{j-1}$ ，但是这 $j$ 组是无序的，所以再除以 $j!$

for (auto p : tot) {
    cnt.push_back(p.second);
}
int sz = tot.size();

dp[0][0] = 1;
for (int i = 1; i <= sz; i++) {
    for (int k = 1; k <= N; k++) {
        for (int j = 1; j <= min((int)cnt[i - 1], k); j++) {
            dp[i][k] = (dp[i][k] + dp[i - 1][k - j] * C(cnt[i - 1] - 1, j - 1LL) % mod
                        * fact[cnt[i - 1]] % mod * infact[j] % mod) % mod;
        }
    }
}
ll ans = 0;
for (ll i = N; i >= 0; i--) {
    ll f = ((N - i) & 1) ? -1LL : 1LL;
    ans +=  f * dp[sz][i] % mod * fact[i] % mod;
    ans = (ans % mod + mod) % mod;
}
printf("%lld\n", ans);

3. 线性DP

1. 1018. 最低通行费

从 $(1, 1)$ 到 $(n, n)$ 找到一个长度为 $2 n - 1$ 的路径使得路径点权之和最小。
这道题也是一个 $N * N$ 的方格。不过行走方向没有限制，但是限制走的步数为 $2 * N - 1$ 步。但是，从 $(1, 1)$ 到 $(N, N)$ 的曼哈顿距离就是 $2 * N - 1$ 啊，所以这道题最少要走 $2 * N - 1$ 步。
不过，这个题求的使最小值，尤其小心边界问题。最小值的话，还是要把 $f$ 初始化为 $I NF$ 的。不然就难以保证从 $(1, 1)$ 进入迷宫。

const int maxn = 110;
int f[maxn][maxn], N;
int main() {   
	memset(f, 0x3f, sizeof f);
	scanf("%d", &N);
	for (int i = 1; i <= N; i++) {
		for (int j = 1; j <= N; j++) {
			scanf("%d", &f[i][j]);
		}
	}
	for (int i = 1; i <= N; i++) {
		for (int j = 1; j <= N; j++) {
			if (i == 1 && j == 1) continue;
			f[i][j] = min(f[i - 1][j] + f[i][j], f[i][j - 1] + f[i][j]);
		}
	}
	printf("%d\n", f[N][N]);
	return 0;
}

2. 482. 合唱队形

这道题是找一个这样的最长子序列： $T_1 < T_2 < ... < T_i > T_{i+1} > T_{i+2} > ...>T_{k}$ 。这个正着求一次最长上升子序列，再倒着求一次最长下降子序列。

#include<bits/stdc++.h>
using namespace std;
const int maxn = 110;
int a[maxn], f1[maxn], f2[maxn];
int N;
int main() {
	scanf("%d", &N);
	for (int i = 1; i <= N; i++) scanf("%d", &a[i]);
	for (int i = 1; i <= N; i++) {
		f1[i] = 1;
		for (int j = 1; j <= i; j++) {
			if (a[j] < a[i]) f1[i] = max(f1[i], f1[j] + 1);
		}
	}
	for (int i = N; i > 0; i--) {
		f2[i] = 1;
		for (int j = N; j >= i; j--) {
			if (a[i] > a[j]) f2[i] = max(f2[i], f2[j] + 1);
		}
	}
	int res = 0;
	for (int i = 1; i <= N; i++) {
		res = max(res, f1[i] + f2[i] - 1);
	}
	printf("%d\n", N - res);
	return 0;
}

3. 编辑距离

题意：给定 $n$ 个长度不超过 $10$ 的字符串以及 $m$ 次询问，每次询问给出长度不超过 $10$ 的一个字符串和一个操作次数上限。对于每次询问，请你求出给定的 $n$ 个字符串中有多少个字符串可以在上限操作次数内经过操作变成询问给出的字符串。每个对字符串进行的单个字符的插入、删除或替换算作一次操作。 $1\le n,m \le 1000$ .

注意这道题，遇到字符串容易出错。我们这道题向函数传入字符串的时候不可以是 s + 1，因为在计算递推式的时候，下标是从1开始的，如果传入s + 1，那么字符串下标其实是从2开始的。

#include<bits/stdc++.h>
using namespace std;
const int N = 1010, M = 15;
char str[N][M];
int f[M][M];
int solve(char a[], char b[])
{
    int l1 = strlen(a + 1), l2 = strlen(b + 1);
    for(int i = 1; i <= l1; i++) f[i][0] = i;
    for(int j = 1; j <= l2; j++) f[0][j] = j;
    for(int i = 1; i <= l1; i++)
    {
        for(int j = 1; j <= l2; j++)
        {
            f[i][j] = min(f[i - 1][j], f[i][j - 1]) + 1;
            f[i][j] = min(f[i][j], f[i - 1][j - 1] + (a[i] != b[j]));
        }
    }
    return f[l1][l2];
}
int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++)
    {
        scanf("%s", str[i] + 1);
    }
    char s[M];
    int limit;
    for(int j = 1; j <= m; j++)
    {
        scanf("%s%d", s + 1, &limit);
        int res = 0;
        for(int i = 1; i <= n; i++)
        {
            res += (solve(str[i], s) <= limit);
        }
        printf("%d\n", res);
    }
    return 0;
}

4. 状态机模型

1057. 股票买卖 IV

给定一个长度为 N 的数组，数组中的第 $i$ 个数字表示一个给定股票在第 $i$ 天的价格。设计一个算法来计算你所能获取的最大利润，你最多可以完成 k 笔交易。
$f (i, j, k)$ ：表示第 $i$ 天，已经进行了 j 次交易，此时的状态为 k 时的收益最大值。 $k = 0$ 表示手中没有股票， $k = 1$ 表示手中有股票。
两个状态，四条有向边，分别对应四个状态转移：
1. $f(i, j, 0) = max\{f(i - 1, j, 0), f(i - 1, j , 1) + w[i]\}$
2. $f(i, j, 1) = max\{f(i - 1, j, 1), f(i - 1, j - 1, 0) - w[i]\}$
关于初始化的问题。如果不初始化为 $- I NF$ ，那么交易了 u 次后，也许收益会变成负数，但是状态会从 0 转移过来。根据实际情况，什么时候收益会是0呢？首先，交易了0次时，收益一定是0，而此时手中一定没有股票。其次，在每一天，都不交易股票，那么收益仍然是0。因此，初始化应是 $\le i \le N$ .

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn = 100010, maxm = 110;
int N, M, w[maxn], f[maxn][maxm][2];
int main() {
	scanf("%d%d", &N, &M);
	//因为状态会有负数，所以要初始化为负无穷。
	memset(f, -0x3f, sizeof f);
	//这个地方初始化注意！
	for (int i = 0; i <= N; i++) f[i][0][0] = 0;

	for (int i = 1; i <= N; i++) scanf("%d", &w[i]);
	for (int i = 1; i <= N; i++) {
		for (int j = 1; j <= M; j++) {
			f[i][j][0] = max(f[i - 1][j][0], f[i - 1][j][1] + w[i]);
			f[i][j][1] = max(f[i - 1][j][1], f[i - 1][j - 1][0] - w[i]);
		}
	}
	int ans = 0;
	for (int j = 1; j <= M; j++) ans = max(f[N][j][0], ans);
	printf("%d\n", ans);
	return 0;
}

1058. 股票买卖 V

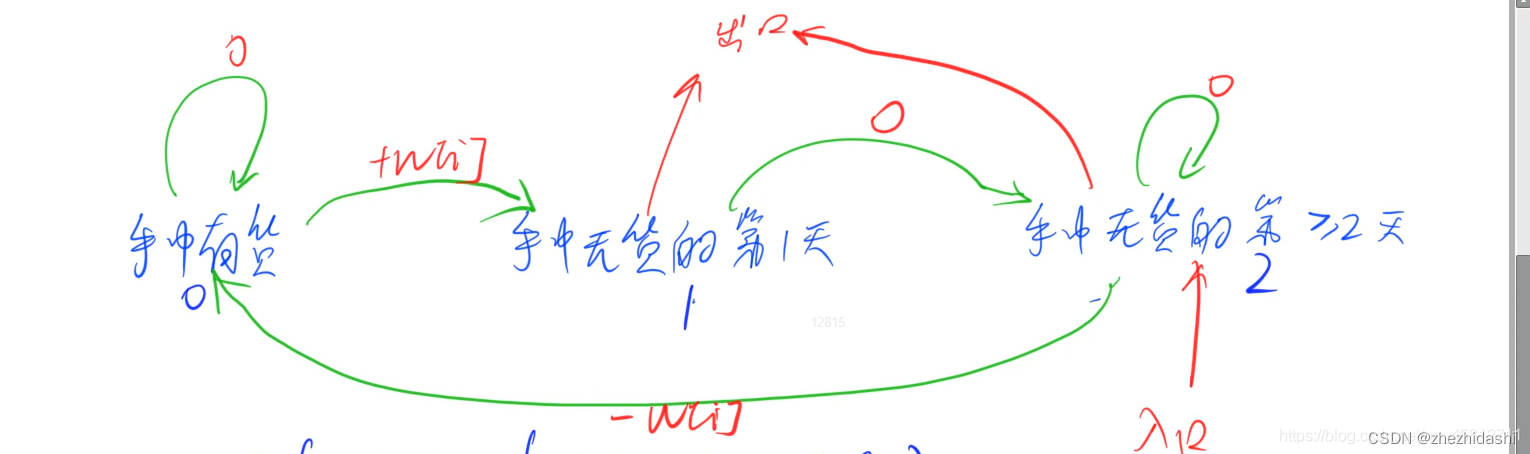
给定一个长度为 N 的数组，数组中的第 i 个数字表示一个给定股票在第 i 天的价格。卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。
这个就是此题的状态机：
于是， $f (i, j)$ 表示在第 $i$ 天，状态为 $j$ 时，收益最大值。 $j = 0$ 表示手中有货， $j = 1$ 表示手中无货第一天， $j = 2$ 表示手中无货 $\ge2$ 天。

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn = 100010, INF = 0x3f3f3f3f;
int f[maxn][3], w[maxn], N;
int main() {
	scanf("%d", &N);
	for (int i = 1; i <= N; i++) {
		scanf("%d", &w[i]);
	}
	memset(f, -0x3f, sizeof f);
	//把入口初始化为0
	f[0][2] = 0;
	for (int i = 1; i <= N; i++) {
		f[i][0] = max(f[i - 1][0], f[i - 1][2] - w[i]);
		f[i][1] = f[i - 1][0] + w[i];
		f[i][2] = max(f[i - 1][2], f[i - 1][1]);
	}
	printf("%d\n", max(f[N][1], f[N][2]));
	return 0;
	
}

5. 状态压缩 DP

6. 区间 DP

320. 能量项链

题意：给 $n$ 个珠子排成一个环，每次可以挑选一颗珠子，把它拿走（假设拿走了第 $i$ 颗石子），释放的能量是 $a_{i-1}*a_i*a_{i+1}$ . 问获得的最大的能量值是多少. 注意这个题最后要合并成一个珠子，如果最后剩两个珠子 $a_i$ 和 $a_j$ ，那么释放的能量将是 $a_i * a_j * a_i$ 或者 $a_j * a_i * a_j$ .

#include<bits/stdc++.h>
using namespace std;
const int N = 210;
int n;
int f[N][N], a[N];
int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; i++)
    {
        scanf("%d", &a[i]);
        a[i + n] = a[i];
    }

    //长度从3开始枚举，到 n + 1
    for(int len = 3; len <= n + 1; len++)
    {
        for(int l = 1, r = l + len - 1; r <= 2 * n; l++, r++)
        {
            //转移节点不能取到左右边界
            for(int k = l + 1; k < r; k++)
            {
                f[l][r] = max(f[l][r], f[l][k] + f[k][r] + a[l] * a[k] * a[r]);
            }
        }
    }
    
    int res = 0;
    // 答案对应的区间长度是 n + 1.
    for(int l = 1, r = l + n; r <= 2 * n; l++, r++)
    {
        res = max(res, f[l][r]);
    }
    printf("%d\n", res);
    return 0;
}

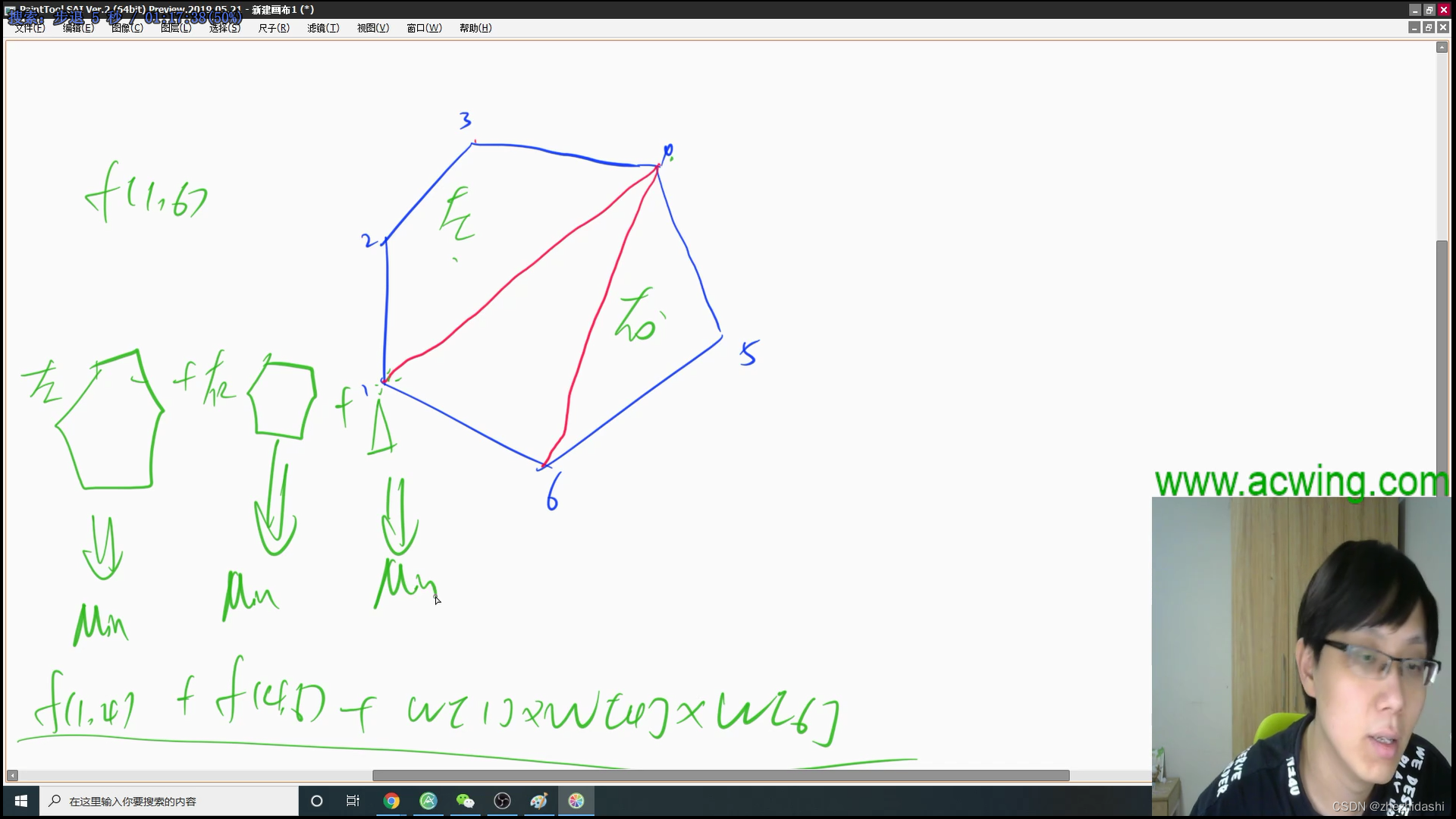
1069. 凸多边形的划分

题意：给定一个具有 $N$ 个顶点的凸多边形，将顶点从 $1$ 至 $N$ 标号，每个顶点的权值都是一个正整数。将这个凸多边形划分成 $N - 2$ 个互不相交的三角形，对于每个三角形，其三个顶点的权值相乘都可得到一个权值乘积，试求所有三角形的顶点权值乘积之和至少为多少。 $\le 50$ ，结点权值均小于 $10^9$ .
可以这样定义。 $f (l, r)$ 为从 $v_l,v_{l+1},v_{l+2},...,v_r$ 这些点组成的多边形的最小权值和。我们假设中转节点是 $k (l < k < r)$ ，那么相当于拆成了 $f(l,k),f(k,r),\triangle v_lv_kv_r$ .
因此这道题实际上是在枚举 $v_lv_r$ 这条边以及中转结点 $v_k$ . 无需将链扩展为两倍就可以写，因为 $f (1, n)$ 已经包含了每一条边. 不过下面的代码还是按照链扩展来写的.

#include<bits/stdc++.h>
using namespace std;
const int N = 110;
const __int128 INF = 1e36;
__int128 f[N][N];
int a[N], n;
void Print(__int128 x)
{
    if(x < 0) 
    {
        putchar('-');
        x = -x;
    }
    if(x > 9) Print(x / 10);
    putchar(x % 10 + '0');
    
}
int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; i++)
    {
        scanf("%d", &a[i]);
        a[i + n] = a[i];
    }
    
    
    for(int len = 3; len <= n; len++)
    {
        for(int l = 1, r = l + len - 1; r <= 2 * n; l++, r++)
        {
            //在这里初始化f更方便
            f[l][r] = INF;
            for(int k = l + 1; k < r; k++)
            {
                
                f[l][r] = min(f[l][r], f[l][k] + f[k][r] + (__int128)a[l] * a[k] * a[r]);
            }
        }
    }
    
    __int128 res = INF;
    for(int l = 1, r = l + n - 1; r <= 2 * n; l++, r++)
    {
        res = min(res, f[l][r]);
    }
    Print(res);
    return 0;
}

479. 加分二叉树

设一个 $n$ 个节点的二叉树 tree 的中序遍历为（ $1, 2, 3, \dots, n$ ），其中数字 $1, 2, 3, \dots, n$ 为节点编号。每个节点都有一个分数（均为正整数），记第 $i$ 个节点的分数为 $d_i$ ，tree 及它的每个子树都有一个加分，任一棵子树 subtree（也包含 tree 本身）的加分计算方法如下：

subtree的左子树的加分 $\times$ subtree的右子树的加分 $＋$ subtree的根的分数

**若某个子树为空，规定其加分为 $1$ 。**叶子的加分就是叶节点本身的分数，不考虑它的空子树。试求一棵符合中序遍历为（ $1, 2, 3, \dots, n$ ）且加分最高的二叉树 tree。

要求输出：（1）tree的最高加分（2）tree的前序遍历。

$f (l, r)$ 表示从中序遍历为 $l$ 到 $r$ 且加分最大的子树的加分值. 因为不改变中序遍历，因此同一棵子树的结点编号一定是连起来的. 那么我们只需要枚举子树的根节点，即 $\min\limits_{l < k < r}\{f(l, k - 1)*f(k + 1,r) + w[k]\}$ . 不过需要注意边界问题，由于子树可能为空，但是子树为空的权值为1，因此需要特殊处理.

#include<bits/stdc++.h>
using namespace std;
const int N = 35, INF = 0x3f3f3f3f;
int f[N][N], g[N][N], w[N];
int n;

void dfs(int l, int r)
{
    int root = g[l][r];
    printf("%d ", root);
    if(l <= root - 1) dfs(l, root - 1);
    if(root + 1 <= r) dfs(root + 1, r);
}

int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; i++) scanf("%d", &w[i]);
    
    for(int len = 1; len <= n; len++)
    {
        for(int l = 1, r = l + len - 1; r <= n; l++, r++)
        {
            //子树大小为1的时候需要注意
            if(l == r) 
            {
                f[l][r] = w[l];
                g[l][r] = l;
            }
            else for(int k = l; k <= r; k++)
            {
                int left = (k == l) ? 1 : f[l][k - 1];
                int right = (k == r) ? 1 : f[k + 1][r];
                int score = left * right + w[k];
                if(f[l][r] < score)
                {
                    f[l][r] = score;
                    g[l][r] = k;
                }
            }
        }
    }
    
    printf("%d\n", f[1][n]);
    
    dfs(1, n);
    return 0;
}

321. 棋盘分割

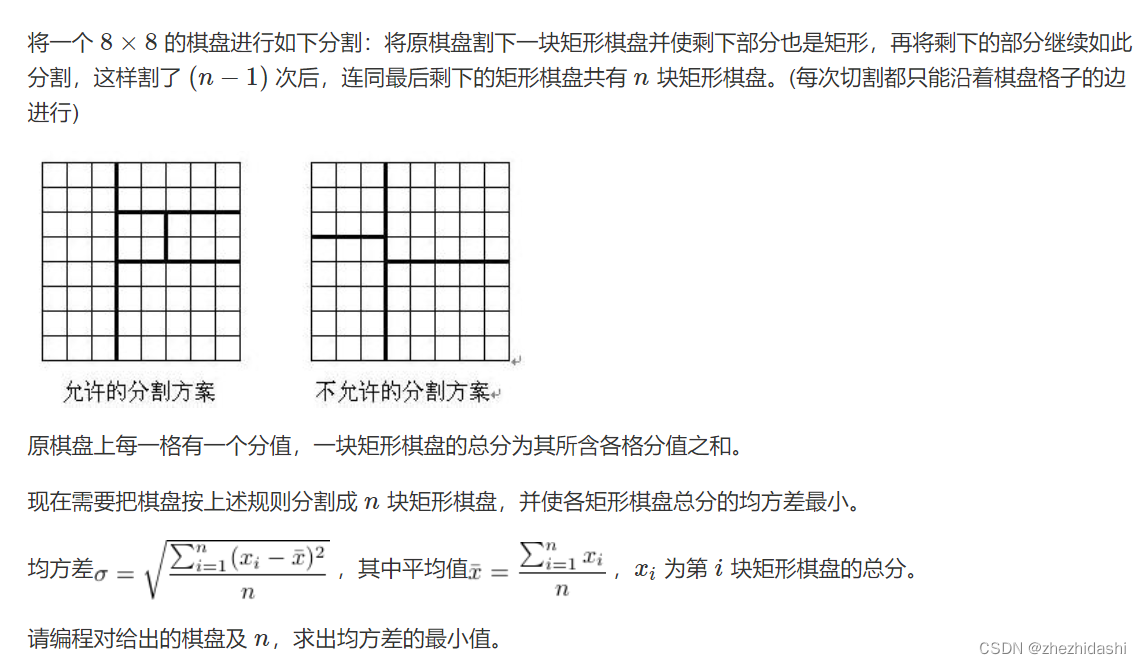
二维区间 DP 问题. 定义 $f(x_1,y_1,x_2,y_2,k)$ 为左上角 $x_1,y_1)$ ，右下角 $x_2,y_2)$ 的矩形切 $k$ 刀后均方差最小值。二维区间 DP 由于状态太多，迭代不好写，因此写为记忆化搜索

由于 $\overline{x}$ 是定值，因此我们只需要让 $\frac{\sum\limits_{i=1}^n (x_i - \overline x)^2}{n}$ 最小即可。对于每一个 $x_1,y_1),(x_2,y_2)$ 的矩形，横着有 $x_2 - x_1 - 1$ 的种方法，可以选择 $2 * (x_2 - x_1 - 1)$ 种方案（扔掉上面的或者下面的），然后被扔掉的那一块儿通过二位前缀和可以迅速求得. 对于列的切割是同理的.

#include<bits/stdc++.h>
using namespace std;
const int N = 15, M = 9, INF = 1e9;
double f[M][M][M][M][N];
int sum[M][M], n;
double X;

double get(int x1, int y1, int x2, int y2)
{
    //X是浮点数，因此 s 一定不要写成 int
    //这里公式没有错，想清楚了
    double s = sum[x2][y2] - sum[x2][y1 - 1] - sum[x1 - 1][y2] + sum[x1 - 1][y1 - 1] - X;
    return s * s / n;
}

double dp(int x1, int y1, int x2, int y2, int k)
{
    double& v = f[x1][y1][x2][y2][k];

    if(v >= 0) return v;
    if(k == 1) return get(x1, y1, x2, y2);

    v = INF;

    for(int i = x1; i < x2; i++)
    {
        v = min(v, dp(x1, y1, i, y2, k - 1) + get(i + 1, y1, x2, y2));
        v = min(v, get(x1, y1, i, y2) + dp(i + 1, y1, x2, y2, k - 1));
    }

    for(int j = y1; j < y2; j++)
    {
        v = min(v, dp(x1, y1, x2, j, k - 1) + get(x1, j + 1, x2, y2));
        v = min(v, get(x1, y1, x2, j) + dp(x1, j + 1, x2, y2, k - 1));
    }
    return v;
}

int main()
{
    scanf("%d", &n);
    memset(f, -1, sizeof f);
    for(int i = 1; i <= 8; i++)
    {
        for(int j = 1; j <= 8; j++)
        {
            scanf("%d", &sum[i][j]);
            //求二位前缀和小心别弄错.
            sum[i][j] += sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1];
        }
    }
    X = (double)sum[8][8] / n;
    printf("%.3f\n", sqrt(dp(1, 1, 8, 8, n)));
    return 0;
}

7.树形DP

1075. 数字转换

题意：如果一个数 $x$ 的约数之和 $y$ （不包括他本身）比他本身小，那么 $x$ 可以变成 $y$ ， $y$ 也可以变成 $x$ 。例如， $4$ 可以变为 $3$ ， $1$ 可以变为 $7$ 。限定所有数字变换在不超过 $n$ 的正整数范围内进行，求不断进行数字变换且不出现重复数字的最多变换步数。 $\le 50000$
这个题形成的是一个可能不连通的无向无环图，但是从一个结点出发往下走，就可以形成一个树的结构. 因此可以相当于找到几棵树的直径的最大值.
至于怎样快速求约数之和。想想怎么样快速筛出所有约数的？

#include<bits/stdc++.h>
using namespace std;
const int N = 50010, M = N * 2;
int f[N];
int h[N], e[M], ne[M], idx;
int n, st[N], ans;
int cnt[N];
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

int dfs(int u, int fa)
{
    st[u] = true;
    int d1 = 0, d2 = 0;
    for(int i = h[u]; i != -1; i = ne[i])
    {
        int v = e[i];
        if(v == fa) continue;
        int d = dfs(v, u) + 1;
        if(d >= d1) d2 = d1, d1 = d;
        else if(d > d2) d2 = d;
    }
    ans = max(ans, d1 + d2);
    return d1;
}

int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; i++)
    {
        for(int j = 2 * i; j <= n; j += i)
        {
            f[j] += i;
        }
    }
    memset(h, -1, sizeof h);
    
    for(int i = 1; i <= n; i++)
    {
        if(i > f[i])
        {
            add(i, f[i]);
            add(f[i], i);
        }
    }
    
    for(int i = 1; i <= n; i++)
    {
        if(!st[i]) dfs(i, -1);
    }
    printf("%d\n", ans);
    return 0;
}

1074. 二叉苹果树

题意：有一棵完全二叉树，这棵树共 $\le 100)$ 个节点，编号为 $1$ 至 $n$ ，树根编号一定为 $1$ 。现在要选出给定数量的边 $v < 100$ ，使得这些边的权值之和最大，并且边上的结点始终与 $1$ 号点连通.
实际上，这就是一个有依赖的背包问题. 把边的终点看作物品，边权就是物品价值，选择的边的数量当作背包容量。然后是容量恰好为 $v$ .

#include<bits/stdc++.h>
using namespace std;
const int N = 110, M = N * 2;

int h[N], e[M], ne[M], w[M], idx;
int n, v, value[N];

void add(int a, int b, int c)
{
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}

int f[N][N], sz[N];
int dfs(int u, int fa)
{
    sz[u] = 1;
    for(int i = h[u]; i != -1; i = ne[i])
    {
        int son = e[i];
        if(son == fa) continue;
        value[son] = w[i];
        sz[u] += dfs(son, u);
        //从大到小循环
        for(int j = min(sz[u] - 1, v - 1); j >= 0; j--)
        {
            for(int k = j; k >= 0; k--)
            {
                f[u][j] = max(f[u][j], f[u][j - k] + f[son][k]);
            }
        }
    }
    //一定要从大到小循环
    for(int j = v; j >= 1; j--)
    {
        f[u][j] = f[u][j - 1] + value[u];
    }

    f[u][0] = 0;
    return sz[u];
}

int main()
{
    scanf("%d%d", &n, &v);
    v++;
    memset(h, -1, sizeof h);
    memset(f, -0x3f, sizeof f);
    for(int i = 1; i <= n; i++) f[i][0] = 0;

    for(int i = 1; i < n; i++)
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c), add(b, a, c);
    }

    dfs(1, -1);
    printf("%d\n", f[1][v]);

    return 0;
}

323. 战略游戏

他必须保护一座中世纪城市，这条城市的道路构成了一棵树 $\le 1500$ 。每个节点上的士兵可以观察到所有和这个点相连的边。他必须在节点上放置最少数量的士兵，以便他们可以观察到所有的边。
这个题的读入很特殊，但是可以采用格式化读入的方式。
然后做法，其实就是和没有上司的舞会一样，只是每个节点的权值是1，要最小化答案.

#include<bits/stdc++.h>
using namespace std;
const int N = 1510, M = N * 2;
int h[N], e[M], ne[M], idx;
int n;
int st[N], f[N][2];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void dfs(int u, int fa)
{
    f[u][0] = 0, f[u][1] = 1;
    for(int i = h[u]; i != -1; i = ne[i])
    {
        int v = e[i];
        if(v == fa) continue;
        dfs(v, u);
        //若不选择u，那么每个v都要选，不然会导致有些边的端点没有选到.
        f[u][0] += f[v][1];
        //选了u之后，v可选可不选.
        f[u][1] += min(f[v][0], f[v][1]);
    }
}

int main()
{
    while(~scanf("%d", &n))
    {
        memset(h, -1, sizeof h);
        idx = 0;
        memset(st, 0, sizeof st);
        for(int i = 1; i <= n; i++)
        {
            int id, cnt;
            scanf("%d:(%d)", &id, &cnt);
            id++;
            while(cnt--)
            {
                int v;
                scanf("%d", &v);
                v++;
                add(id, v), add(v, id);
                st[v] = true;
            }
        }
        dfs(1, -1);
        printf("%d\n", min(f[1][0], f[1][1]));
    }
    return 0;
}

8.数位统计DP

1083. Windy数

题意：不含前导零且相邻两个数字之差至少为 2 的正整数被称为 Windy 数。Windy 想知道，在 A 和 B 之间，包括 A 和 B，总共有多少个 Windy 数？

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
const int maxn = 11;
int f[maxn][10];
//f[i][j] 保存的是 i 位最高位的数字是 j 的满足要求的数字的个数。
//这个答案是准确的，至于前导零怎么考虑，是在dp函数里面利用这个算的。
int dp(int n) {
	if (n == 0) return 0;  // 这道题的 0 不在考虑范围内
	vector<int> nums;
	while (n) nums.push_back(n % 10), n /= 10;
	int last = -2, res = 0;
	for (int i = nums.size() - 1; i >= 0; i--) {
		int x = nums[i];
		for (int j = i == nums.size() - 1; j < x; j++) {
			if (abs(j - last) >= 2) {
				res += f[i + 1][j];
			}
		}
		if (abs(x - last) >= 2) last = x;
		else break;

		if (i == 0) res++;
	}

	// 特殊处理有前导零的数
	for (int i = 1; i < nums.size(); i++) {
		for (int j = 1; j <= 9; j++) {
			res += f[i][j];
		}
	}
	return res;
}
int main() {
	//预处理
	//这里，应该从0开始枚举。尽管0不在计算之内，但是如果不算0的话，有些状态转移不过来
	//比如，f[2][2]，从f[1][0]转移，f[2][2]应该包含20这个数字，如果f[1][0]=0，这个数就转移不过来了
    //但是在算res时，研究dp就会发现，0这个数字是不会算进去的。
	for (int j = 0; j <= 9; j++) f[1][j] = 1;
	for (int i = 2; i < maxn; i++) {
		for (int j = 0; j <= 9; j++) {
			for (int k = 0; k <= 9; k++) {
				if (abs(j - k) >= 2) {
					f[i][j] += f[i - 1][k];
				}
			}
		}
	}
	
	int a, b;
	cin >> a >> b;
	cout << dp(b) - dp(a - 1) << endl;

	return 0;
}

深搜代码

#include<bits/stdc++.h>
using namespace std;
const int N = 35;
int f[N][N][2], a[N];
int A, B;

int dp(int pos, int k, int flag, int lim)
{
    if(pos == -1) return 1;
    if(!lim && f[pos][k][flag] != -1) return f[pos][k][flag];
    int up = lim ? a[pos] : 9;
    int ans = 0;
    for(int i = 0; i <= up; i++)
    {
        if(!flag && abs(i - k) >= 2) ans += dp(pos - 1, i, flag, i == up && lim);
        if(flag) ans += dp(pos - 1, i, i == 0 && flag, i == up && lim);
    }
    if(!lim) f[pos][k][flag] = ans;
    return ans;
}

int solve(int x)
{
    int sz = 0;
    while(x)
    {
        a[sz++] = x % 10;
        x /= 10;
    }
    //千万别忘记初始化
    memset(f, -1, sizeof f);
    return dp(sz - 1, 0, 1, 1);
}

int main()
{
    scanf("%d%d", &A, &B);
    //printf("*** %d\n*** %d\n", solve(A - 1), solve(B));
    printf("%d\n", solve(B) - solve(A - 1));
}

1084. 数字游戏 II

某人又命名了一种取模数，这种数字必须满足各位数字之和 mod N 为 0。现在大家又要玩游戏了，指定一个整数闭区间 $[a, b]$ ，问这个区间内有多少个取模数。
难点还是在预处理过程.
设 $f (i, j, k)$ 是有 $i$ 位，最高位是 $j$ ，且模 N 为 k 的数字的数量。 $\sum\limits_{x=0}^{9} f(i-1, x, (k-j)\ mod\ N)$ .

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
int f[11][10][110];
int P;
int mod(int x, int y) {
	return (x % y + y) % y;
}
int dp(int n) {
	if (n == 0) return 1;
	vector<int> nums;
	while (n) {
		nums.push_back(n % 10);
		n /= 10;
	}
	int res = 0, last = 0; //last 存左面各分支数字之和。
	for (int i = nums.size() - 1; i >= 0; i--) {
		int x = nums[i];
		for (int j = 0; j < x; j++) {
			res += f[i + 1][j][mod(-last, P)];
		}
		last += x;
		if (i == 0 && (last % P == 0)) res++;
	}
	return res;
}
void init() {
	memset(f, 0, sizeof f);
	for (int j = 0; j <= 9; j++) f[1][j][j % P]++;
	for (int i = 2; i < 11; i++) {
		for (int j = 0; j <= 9; j++) {
			for (int k = 0; k < P; k++) {
				for (int x = 0; x <= 9; x++) {
					f[i][j][k] += f[i - 1][x][mod(k - j, P)];
				}
			}
		}
	}
}
int main() {
	
	int l, r;
	while (cin >> l >> r >> P) {
		init();
		cout << dp(r) - dp(l - 1) << endl;
	}
}

深搜代码

#include<bits/stdc++.h>
using namespace std;
const int N = 35, M = 110;
int f[N][M], a[N];
int A, B, mod;

int dp(int pos, int k, int lim)
{
    if(pos == -1) return k == 0;
    if(!lim && f[pos][k] != -1) return f[pos][k];
    int ans = 0, up = lim ? a[pos] : 9;
    for(int i = 0; i <= up; i++)
    {
        ans += dp(pos - 1, (k + i) % mod, i == up && lim);
    }
    if(!lim) f[pos][k] = ans;
    return ans;
}

int solve(int x)
{
    int sz = 0;
    while(x)
    {
        a[sz++] = x % 10;
        x /= 10;
    }
    memset(f, -1, sizeof f);
    return dp(sz - 1, 0, 1);
}

int main()
{
    ios::sync_with_stdio(0);
    while(cin >> A >> B >> mod)
    {
        cout << solve(B) - solve(A - 1) << endl;
    }
}

J. Junior Mathematician

感觉这个题又是一个 $d p$ 的板子，有时候用大雪菜的方法并不好处理状态不含数位的情况。就比如这个，不含第 i 位数字是几的信息，因此没办法处理后面的步骤。
题意：求 $\le 10^{5000})$ 间满足 $\equiv f(x) \bmod m (m \le 60)$ 的数量。 $f (x)$ 表示所有数位两两之积的和。
$d p (i, s u m, res)$ ：第 $i$ 位，当前数字之和是 $s u m$ ，当前 $f (x) - x$ 为 $res$
这样子的话，我们用深搜去搜索答案。和大雪菜的思路差不多，从最高位开始搜， $df s$ 中间那一大块儿，不同的数位 $d p$ 都是一样的。

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>

typedef long long ll;
const ll mod = 1e9 + 7;
using namespace std;
const int maxn = 5010;
char s1[maxn], s2[maxn];
int M;
int f[maxn][60][60], p[maxn], a[maxn];
int my_mod(int a, int b) {
	return (a % b + b) % b;
}

int dp(int pos, int sum, int res, bool limit) {
	// lim=1 表示当前贴合上界，lim=0 则不贴合
	if (pos == -1) {
		return res == 0;
	}
	if (limit == false && f[pos][sum][res] != -1) {
		return f[pos][sum][res];
	}
	else {
		int ans = 0, up = limit ? a[pos] : 9;
		for (int i = 0; i <= up; i++) {
			int xx = my_mod(res + sum * i - i * p[pos], M);
			ans = (ans + dp(pos - 1, my_mod(sum + i, M), xx, (i == up) && limit)) % mod;
		}
		if (limit == false) {  // 不贴合上界的情况有可能会被复用
			f[pos][sum][res] = ans;
		}
		return ans;
	}
}

int solve(char s[], int n) {
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < M; j++) {
			memset(f[i][j], -1, sizeof f[i][j]);
		}
	}
	for (int i = 0; i < n; i++) {
		a[i] = s[n - i - 1];
	}
	//这个方法也是从高数位往低数位填数字
	return dp(n - 1, 0, 0, 1);
}

int main() {
	int T;
	scanf("%d", &T);

	while (T--) {
		scanf("%s%s%d", s1, s2, &M);
		int n1 = strlen(s1), n2 = strlen(s2);

		for (int i = 0; i < n1; i++) s1[i] -= '0';
		for (int i = 0; i < n2; i++) s2[i] -= '0';
		s1[n1 - 1]--;
		for (int i = n1 - 1; i >= 0; i--) {
			if (s1[i] < 0) {
				s1[i] += 10;
				s1[i - 1]--;
			}
			else break;
		}

		//for (int i = 0; i < n1; i++) printf("%d", s1[i]);

		p[0] = 1;
		for (int i = 1; i < maxn; i++) {
			p[i] = p[i - 1] * 10 % M;
		}
		//printf("*** %d %d\n", solve(s2, n2), solve(s1, n1));
		printf("%d\n", my_mod(solve(s2, n2) - solve(s1, n1), mod));
	}
	return 0;
}

D. Beautiful numbers

再来一道深搜处理数位 $d p$ 的题目。
题意：Beautiful Numbers定义为这个数能整除它的所有位上非零整数。问[l,r]之间的Beautiful Numbers的个数。
数位 DP: 数位 DP 问题往往都是这样的题型，给定一个闭区间 $[l, r]$ ，让你求这个区间中满足某种条件的数的总数。我们将问题转化成更加简单的形式。设 $ans_i$ 表示在区间中满足条件的数的数量，那么所求的答案就是 $ans_{r} - ans_{l - 1}$ .
看代码吧，可以发现所有个位数的最小公倍数是2520，dfs(len, sum, lcm, limit) ，len表示迭代的长度，sum为截止当前位的数对2520取余后的值。 lcm为截止当前位的所有数的最小公倍数。limit表示当前数是否可以任意取值(对取值上限进行判断).
代码其实很好懂，但是方法确实不是那么好想。

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxlcm = 2520;
typedef long long ll;
ll dp[20][50][2530];
int Hash[2530];
ll nums[20];
ll gcd(ll a, ll b) {
	if (b == 0) return a;
	return gcd(b, a % b);
}
ll dfs(ll pos, ll sum, ll lcm, bool limit) {
	if (pos == -1) {
		return sum % lcm == 0;
	}
	if (limit == false && dp[pos][Hash[lcm]][sum] != -1) return dp[pos][Hash[lcm]][sum];
	ll ans = 0;
	int up = limit ? nums[pos] : 9;
	for (int i = 0; i <= up; i++) {
		ans += dfs(pos - 1, (sum * 10 + i) % maxlcm, i ? i * lcm / gcd((ll)i, lcm) : lcm, limit && i == up);
	}
	if (limit == 0) dp[pos][Hash[lcm]][sum] = ans;
	return ans;
}
ll solve(ll N) {
	int p = 0;
	while (N) {
		nums[p++] = N % 10;
		N /= 10;
	}
	return dfs(p - 1, 0, 1, true);
}
int main() {
	int T;
	scanf("%d", &T);
	memset(dp, -1, sizeof dp);
	int cnt = 0;
	for (int i = 1; i <= maxlcm; i++) {
		if (maxlcm % i == 0) Hash[i] = cnt++;
	}
	while (T--) {
		ll l, r;
		cin >> l >> r;
		cout << solve(r) - solve(l - 1) << endl;
	}
	return 0;
}