1 理论基础
1.1 三维路径规划问题概述
三维路径规划指在已知三维地图中,规划出一条从出发点到目标点满足某项指标最优,并且避开了所有三维障碍物的三维最优路径。现有的路径规划算法中,大部分算法是在二维规划平面或准二维规划平面中进行路径规划。一般的三维路径规划算法具有计算过程复杂、信息存储量大、难以直接进行全局规划等问题。已有的三维路径规划算法主要包括A*算法、遗传算法、粒子群算法等,但是A*算法的计算量会随着维数的增加而急剧增加,遗传算法和粒子群算法只是准三维规划算法。
蚁群算法具有分布计算、群体智能等优势,在路径规划上具有很大潜力,在成功用于二维路径规划的同时也可用于三维路径规划,本章采用蚁群算法进行水下机器人三维路径规划。
1.2 三维空间抽象建模
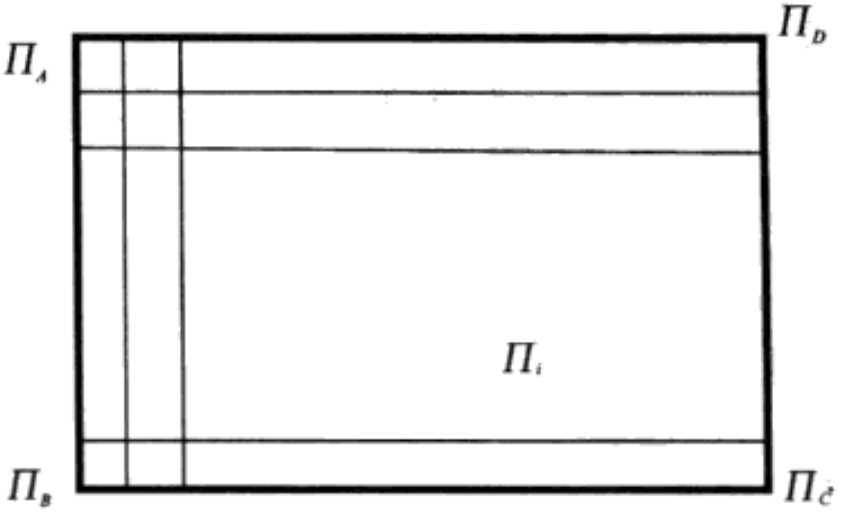
三维路径规划算法首先需要从三维地图中抽象出三维空间模型,模型抽象方法如下:首先把三维地图左下角的顶点作为三维空间的坐标原点A,在点A中建立三维坐标系,其中,x轴为沿经度增加的方向,y轴为沿纬度增加的方向,z轴为垂直于海平面方向。在该坐标系中以点A为顶点,沿x轴方向取三维地图的最大长度AB,沿y轴方向取三维地图的最大长度AA',沿z轴方向取三维地图的最大长度AB,这样就构造了包含三维地图的立方体区域ABCD-A'B'C'D',该区域即为三维路径的规划空间。三维路径规划空间如图1所示。三维路径空间建立起来之后,采用等分空间的方法从三维空间中抽取出三维路径规划所需的网格点。首先沿边AB把规划空间ABCD-A'B'C'D'进行等分,得到n+1个平面Ⅱi(i=1,2,…,n),然后对这n+1个平面沿边AD进行m等分,沿边AA'进行l等分,并且求解出里面的交点。平面划分如图2所示。
通过以上步骤,整个规划空间ABCD-A'B'’C'D'就离散化为一个三维点集合,集合中的任意一点对应着两个坐标,即序号坐标a1(i,j,k)(i=0,1,2,…,n,j=0,1,2,…,m,k=0,1,2, …,l)和位置坐标a2 (xi ,yi, zi), 其中,i,j,k分别为当前点a沿边AA,边AD,边AA'的划分序号。蚁群算法即在这些三维路径点上进行规划,最终得到连接出发点和目标点满足某项指标最优的三维路径。

 2案例背景
2案例背景
2.1问题描述
采用蚁群算法在跨度为21 km×21 km的一片海域中搜索从起点到终点,并且避开所有障碍物的路径,为了方便问题的求解,取该区域内最深点的高度为0,其他点高度根据和最深点高度差依次取得。路径规划起点坐标为(1,10,800),终点坐标为(21,4,1 000),规划环境和起点、终点如图3所示。整个搜索空间为21 km×21 km的海域,其中,起点坐标为(1,10,800),终点坐标为(21,4,1 000)。
基于蚁群算法的三维路径搜索算法的算法流程如图4所示。

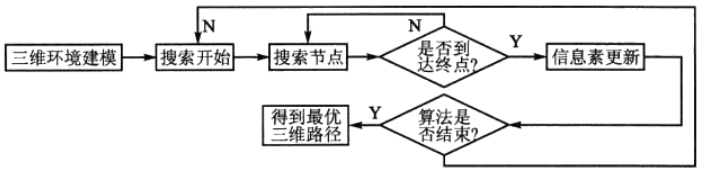
其中,三维环境建模模块根据1.2节抽取出三维环境数学模型;搜索节点模块根据启发函数搜索下个节点;信息素更新模块更新环境中节点的信息素值。
2.3 信息素更新
蚁群算法使用信息素吸引蚂蚁搜索,信息素位置设定及更新方法对于蚁群算法的成功搜索具有非常重要的意义。在1.2节中已经把整个搜索空间离散为一系列的三维离散点,这些离散点为蚁群算法需要搜索的节点。因此,把信息素存储在模型的离散点中,每个离散点都有一个信息素的值,该点信息素的大小代表对蚂蚁的吸引程度,各点信息素在每只蚂蚁经过后进行更新。信息素的更新包括局部更新和全局更新两部分,局部更新是指当蚂蚁经过该点时,该点的信息素就减少,局部更新的目的是增加蚂蚁搜索未经过点的概率,达到全局搜索的目的。局部信息素更新随着蚂蚁的搜索进行,信息素更新公式为
 2.4可视搜索空间
2.4可视搜索空间
取α轴方向作为三维路径规划的主方向,水下机器人沿工轴方向前进,为了降低规划复杂程度,将水下机器人的运动简化为前向运动、横向运动和纵向运动三种运动方式。在前向运动一定单位长度距离Lx,max情况下,设定机器人最大横向移动允许距离为Ly,max,最大纵向移动距离为Lz,max。这样,当蚂蚁沿着α轴方向前进时,当位于点H(i,j,k)时,对下一个点的搜索就存在一个可视区域,可视区域如图5所示。

这样,当蚂蚁由当前点向下一个点移动时,可搜索的区域限制在蚂蚁搜索可视区域之内,简化了搜索空间,提高了蚁群算法的搜索效率。
2.5 蚁群搜索策略
蚂蚁从当前点移动到下一个点时,根据启发函数来计算可视区域内各点的选择概率,启发函数为


3 MATLAB程序
根据蚁群算法原理,在MATLAB中编程实现基于蚁群算法的三维路径规划算法。
3.1 启发值计算函数
该函数主要用于计算可视区域内各点的启发值。
function qfz=CacuQfz(Nexty,Nexth,Nowy,Nowh,endy,endh,abscissa,HeightData)
%% 该函数用于计算各点的启发值
%Nexty Nexth input 下个点坐标
%Nowy Nowh input 当前点坐标
%endy endh input 终点坐标
%abscissa input 横坐标
%HeightData input 地图高度
%qfz output 启发值
%% 判断下个点是否可达
if HeightData(Nexty,abscissa)<Nexth*200
S=1;
else
S=0;
end
%% 计算启发值
%D距离
D=50/(sqrt(1+(Nowh*0.2-Nexth*0.2)^2+(Nexty-Nowy)^2)+sqrt((21-abscissa)^2 ...
+(endh*0.2-Nexth*0.2)^2+(endy-Nowy)^2));
%计算高度
M=30/abs(Nexth+1);
%计算启发值
qfz=S*M*D;3.2适应度计算函数
适应度计算函数主要用于计算每条路径的适应度值。
function fitness=CacuFit(path)
%% 该函数用于计算个体适应度值
%path input 路径
%fitness input 路径
[n,m]=size(path);
for i=1:n
fitness(i)=0;
for j=2:m/2
%适应度值为长度加高度
fitness(i)=fitness(i)+sqrt(1+(path(i,j*2-1)-path(i,(j-1)*2-1))^2 ...
+(path(i,j*2)-path(i,(j-1)*2))^2)+abs(path(i,j*2));
end
end3.3 路径搜索
路径搜索函数采用蚁群算法根据信息素和启发值搜索从出发点到终点的三维路径。
function [path,pheromone]=searchpath(PopNumber,LevelGrid,PortGrid,pheromone,HeightData,starty,starth,endy,endh)
%% 该函数用于蚂蚁蚁群算法的路径规划
%LevelGrid input 横向划分格数
%PortGrid input 纵向划分个数
%pheromone input 信息素
%HeightData input 地图高度
%starty starth input 开始点
%path output 规划路径
%pheromone output 信息素
%% 搜索参数
ycMax=2; %蚂蚁横向最大变动
hcMax=2; %蚂蚁纵向最大变动
decr=0.9; %信息素衰减概率
%% 循环搜索路径
for ii=1:PopNumber
path(ii,1:2)=[starty,starth]; %记录路径
NowPoint=[starty,starth]; %当前坐标点
%% 计算点适应度值
for abscissa=2:PortGrid-1
%计算所有数据点对应的适应度值
kk=1;
for i=-ycMax:ycMax
for j=-hcMax:hcMax
NextPoint(kk,:)=[NowPoint(1)+i,NowPoint(2)+j];
if (NextPoint(kk,1)<20)&&(NextPoint(kk,1)>0)&&(NextPoint(kk,2)<20)&&(NextPoint(kk,2)>0)
qfz(kk)=CacuQfz(NextPoint(kk,1),NextPoint(kk,2),NowPoint(1),NowPoint(2),endy,endh,abscissa,HeightData);
qz(kk)=qfz(kk)*pheromone(abscissa,NextPoint(kk,1),NextPoint(kk,2));
kk=kk+1;
else
qz(kk)=0;
kk=kk+1;
end
end
end
%选择下个点
sumq=qz./sum(qz);
pick=rand;
while pick==0
pick=rand;
end
for i=1:25
pick=pick-sumq(i);
if pick<=0
index=i;
break;
end
end
oldpoint=NextPoint(index,:);
%更新信息素
pheromone(abscissa+1,oldpoint(1),oldpoint(2))=0.5*pheromone(abscissa+1,oldpoint(1),oldpoint(2));
%路径保存
path(ii,abscissa*2-1:abscissa*2)=[oldpoint(1),oldpoint(2)];
NowPoint=oldpoint;
end
path(ii,41:42)=[endy,endh];
end3.4 主函数
主函数主要用于蚁群算法的全局寻优,通过迭代寻找全局最优解,主要程序如下:
%% 该函数用于演示基于蚁群算法的三维路径规划算法
%% 清空环境
clc
clear
%% 数据初始化
%下载数据
load HeightData HeightData
%网格划分
LevelGrid=10;
PortGrid=21;
%起点终点网格点
starty=10;starth=4;
endy=8;endh=5;
m=1;
%算法参数
PopNumber=10; %种群个数
BestFitness=[]; %最佳个体
%初始信息素
pheromone=ones(21,21,21);
%% 初始搜索路径
[path,pheromone]=searchpath(PopNumber,LevelGrid,PortGrid,pheromone, ...
HeightData,starty,starth,endy,endh);
fitness=CacuFit(path); %适应度计算
[bestfitness,bestindex]=min(fitness); %最佳适应度
bestpath=path(bestindex,:); %最佳路径
BestFitness=[BestFitness;bestfitness]; %适应度值记录
%% 信息素更新
rou=0.2;
cfit=100/bestfitness;
for i=2:PortGrid-1
pheromone(i,bestpath(i*2-1),bestpath(i*2))= ...
(1-rou)*pheromone(i,bestpath(i*2-1),bestpath(i*2))+rou*cfit;
end
%% 循环寻找最优路径
for kk=1:100
%% 路径搜索
[path,pheromone]=searchpath(PopNumber,LevelGrid,PortGrid,...
pheromone,HeightData,starty,starth,endy,endh);
%% 适应度值计算更新
fitness=CacuFit(path);
[newbestfitness,newbestindex]=min(fitness);
if newbestfitness<bestfitness
bestfitness=newbestfitness;
bestpath=path(newbestindex,:);
end
BestFitness=[BestFitness;bestfitness];
%% 更新信息素
cfit=100/bestfitness;
for i=2:PortGrid-1
pheromone(i,bestpath(i*2-1),bestpath(i*2))=(1-rou)* ...
pheromone(i,bestpath(i*2-1),bestpath(i*2))+rou*cfit;
end
end
%% 最佳路径
for i=1:21
a(i,1)=bestpath(i*2-1);
a(i,2)=bestpath(i*2);
end
figure(1)
x=1:21;
y=1:21;
[x1,y1]=meshgrid(x,y);
mesh(x1,y1,HeightData)
axis([1,21,1,21,0,2000])
hold on
k=1:21;
plot3(k(1)',a(1,1)',a(1,2)'*200,'--o','LineWidth',2,...
'MarkerEdgeColor','k',...
'MarkerFaceColor','g',...
'MarkerSize',10)
plot3(k(21)',a(21,1)',a(21,2)'*200,'--o','LineWidth',2,...
'MarkerEdgeColor','k',...
'MarkerFaceColor','g',...
'MarkerSize',10)
text(k(1)',a(1,1)',a(1,2)'*200,'S');
text(k(21)',a(21,1)',a(21,2)'*200,'T');
xlabel('km','fontsize',12);
ylabel('km','fontsize',12);
zlabel('m','fontsize',12);
title('三维路径规划空间','fontsize',12)
set(gcf, 'Renderer', 'ZBuffer')
hold on
plot3(k',a(:,1)',a(:,2)'*200,'--o')
%% 适应度变化
figure(2)
plot(BestFitness)
title('最佳个体适应度变化趋势')
xlabel('迭代次数')
ylabel('适应度值')3.5 仿真结果
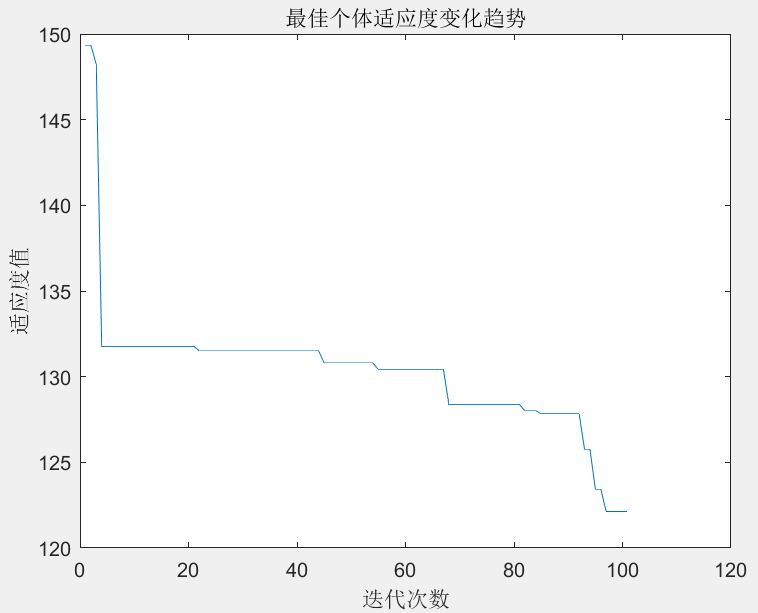
采用蚁群算法进行三维路径规划,规划空间范围为20km×20 km的海域,根据1.2节的内容把规划空间抽象为21km×21km×21km的规划空间,其中,x轴,y轴方向每个节点的间距为1km,z轴方向每个节点间距为200m。路径起点在规划空间的序号为[1 10 4], 终点在规划空间的序号为[21 4 5]。算法的基本设置为种群规模为20,算法迭代为400次,路径规划结果和最优个体适应度变化如图6和图7所示。

4 总结
以蚁群算法为代表的群智能已成为当今分布式人工智能研究的一个热点,许多源于蜂群和蚁群模型设计的算法已越来越多地被应用于企业的运转模式的研究。美国五角大楼正在资助关于群智能系统的研究工作——群体战略(swarm strategy),它的一个实战用途是通过运用成群的空中无人驾驶飞行器和地面车辆来转移敌人的注意力,让自己的军队在敌人后方不被察觉地安全活动。英国电信公司和美国世界通信公司以电子蚂蚁为基础,对新的电信网络管理方法进行了试验。群智能还被应用于工厂生产计划的制订和运输部门的后勤管理。美国太平洋西南航空公司采用了一种直接源于蚂蚁行为研究成果的运输管理软件,结果每年至少节约1000万美元的费用开支。英国联合利华公司率先利用群智能技术改善其一家牙膏厂的运转情况。美国通用汽车公司、法国液气公司、荷兰公路交通部和美国一些移民事务机构也都采用这种技术来改善其运转。
5.完整代码
基于蚁群算法的三维路径规划(matlab实现)