当谈到计算机科学时，算法是一个重要的话题，因为它们能帮助解决很多问题。而有些算法，其高效性和惊人表现，令人感到惊艳。一起来分享一下你认为令人惊艳的高效算法吧！

一、你在工作和学习中用到过哪些惊艳的算法？（包括但不限于数据科学、计算机视觉、自然语言处理等多个领域的算法）

Dijkstra算法： 一种用于寻找图中单源最短路径的贪心算法。

二、请你介绍一下上述算法并进行一下简单演示吧！

1. Dijkstra 是什么？

  Dijkstra算法是一种用于寻找图中单源最短路径的贪心算法。它通过不断扩展距离当前源点最近的节点来确定下一个待处理的节点，直到找到目标节点为止。
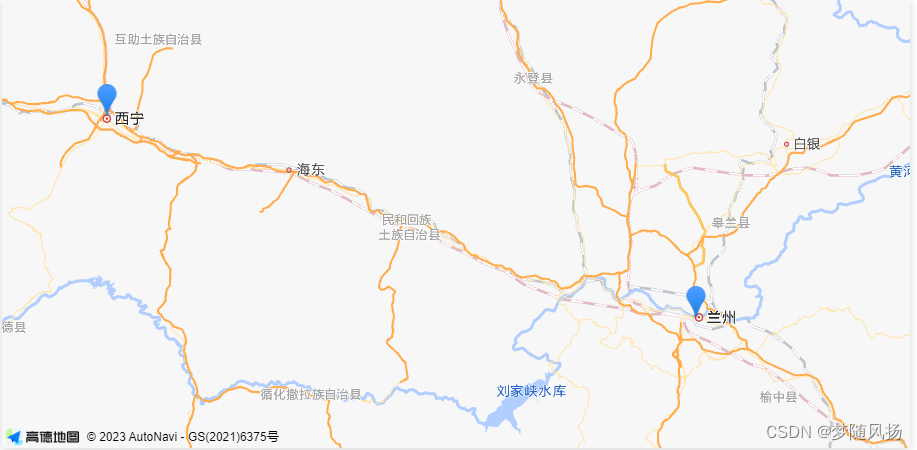
譬如下图 假如路径和长度已知，那么可以使用dijkstra算法计算西宁到图中所有节点的最短距离。

2. Dijkstra 算法过程

  Dijkstra算法的过程如下：

初始化：假设有n个顶点，每个顶点都有一个表示到源点的距离的数组dist。将所有顶点的dist初始化为无穷大，源点的距离设为0。

选择当前距离源点最近的未确定节点u。

更新与u相邻的所有节点的dist值，如果发现更短的路径，则更新它们的dist值。

重复步骤2和3,直到找到目标节点或所有的节点都被处理过。

返回dist数组作为结果，其中dist[i]表示从源点到顶点i的最短距离。

---

图解：

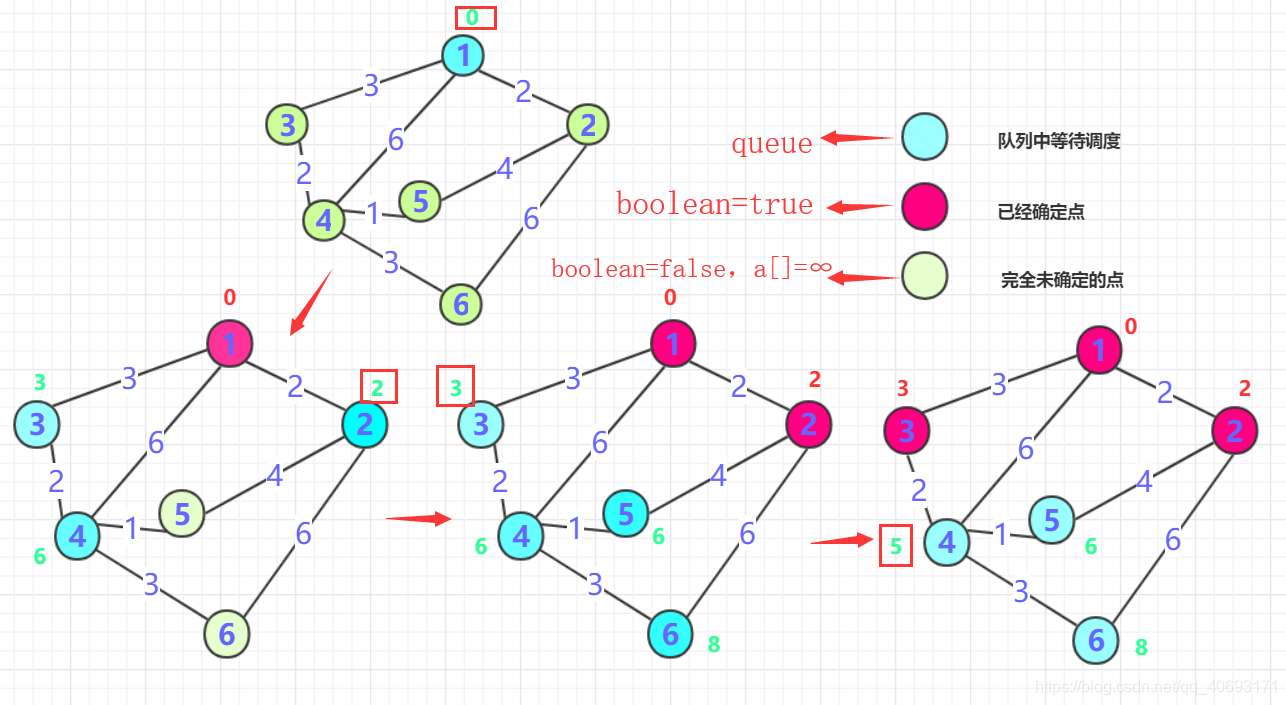
• 重复二的操作，直到所有点都确定。
  

• ---

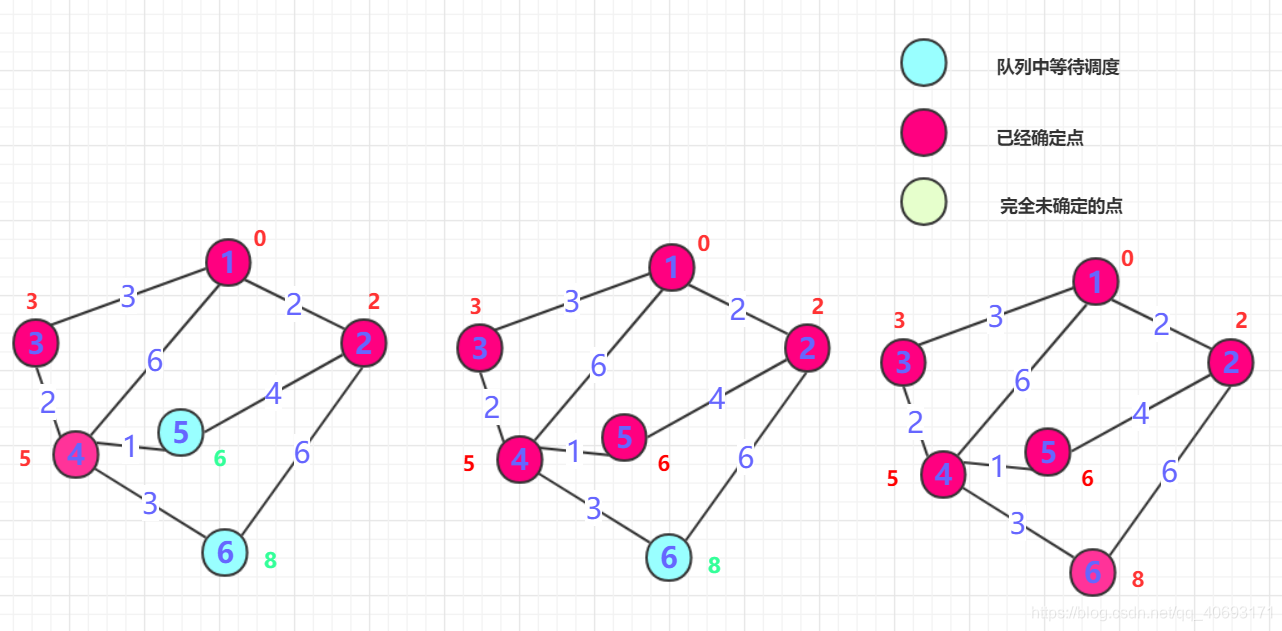
  Dijkstra算法的时间复杂度为O(n^2), 用图来说明就是：

    假设有如下无向图，其中每条边的边权均为正整数。

  A-B-C-D-E
  |         |
  F         G
  
  

    我们要计算从顶点A到顶点E的最短路径长度。可以使用Dijkstra算法来实现。
  首先，将所有顶点的dist值初始化为无穷大，源点的距离设为0。然后选择当前距离源点最近的未确定节点u。在这个例子中，选择顶点A作为当前处理的节点。

       u       v       dist    A->E
  A       B       1      0   / \     / \
  A       C       2      1   |   |     |
  A       D       3      2   |   |     |
  A       E       4      3   |   |     |
  B       C       2      1  / \    / \     |
  B       D       3      2  / \    / \     |
  B       E       4      3  / \    / \     |
  C       D       3      2     |   |     |
  C       E       4      3     |   |     |
  D       E       4      3     |   |     |
  
  

    接下来，我们需要更新与u相邻的所有节点的dist值，如果发现更短的路径，则更新它们的dist值。在这个例子中，我们需要更新顶点B、C和D的dist值。具体来说，我们需要将顶点B、C和D分别与顶点A相连的边权进行比较，如果发现更短的路径，则更新它们的dist值。最终得到的结果如下所示：

       u       v       dist    A->E
  A       B       1      0   / \     / \
  A       C       2      1   |   |     |
  A       D       3      2   |   |     |
  A       E       4      3   |   |     |
  B       C       2      1  / \    / \     |
  B       D       3      2  / \    / \     | // 将B的dist更新为1,因为它与A相连的边的边权更小
  B       E       4      3  / \    / \     | // 将B的dist更新为1,因为它与A相连的边的边权更小
  C       D       3      2     |   |     | // 将C的dist更新为2,因为它与A相连的边的边权更小
  C       E       4      3     |   |     | // 将C的dist更新为2,因为它与A相连的边的边权更小
  D       E       4      3     |   |     | // 将D的dist更新为3,因为它与A相连的边的边权更小
  
  

    最后，我们得到了一个长度为4的dist数组，表示从源点A到顶点E的最短路径长度。

  ---

  3. 算法实现：

  package 图论;
  
  import java.util.ArrayDeque;
  import java.util.Comparator;
  import java.util.PriorityQueue;
  import java.util.Queue;
  import java.util.Scanner;
  
  public class dijkstra {
  	static class node
  	{
  		int x; //节点编号
  		int lenth;//长度
  		public node(int x,int lenth) {
  			this.x=x;
  			this.lenth=lenth;
  		}
  	}
  
  	public static void main(String[] args) {
  		 
  		int[][] map = new int[6][6];//记录权值，顺便记录链接情况，可以考虑附加邻接表
  		initmap(map);//初始化
  		boolean bool[]=new boolean[6];//判断是否已经确定
  		int len[]=new int[6];//长度
  		for(int i=0;i<6;i++)
  		{
  			len[i]=Integer.MAX_VALUE;
  		}
  		Queue<node>q1=new PriorityQueue<node>(com);
  		len[0]=0;//从0这个点开始
  		q1.add(new node(0, 0));
  		int count=0;//计算执行了几次dijkstra
  		while (!q1.isEmpty()) {
  			node t1=q1.poll();
  			int index=t1.x;//节点编号
  			int length=t1.lenth;//节点当前点距离
  			bool[index]=true;//抛出的点确定
  			count++;//其实执行了6次就可以确定就不需要继续执行了  这句可有可无，有了减少计算次数
  			for(int i=0;i<map[index].length;i++)
  			{
  				if(map[index][i]>0&&!bool[i])
  				{
  					node node=new node(i, length+map[index][i]);
  					if(len[i]>node.lenth)//需要更新节点的时候更新节点并加入队列
  					{
  						len[i]=node.lenth;
  						q1.add(node);
  					}
  				}
  			}
  		}		
  		for(int i=0;i<6;i++)
  		{
  			System.out.println(len[i]);
  		}
  	}
  	static Comparator<node>com=new Comparator<node>() {
  
  		public int compare(node o1, node o2) {
  			return o1.lenth-o2.lenth;
  		}
  	};
  
  	private static void initmap(int[][] map) {
  		map[0][1]=2;map[0][2]=3;map[0][3]=6;
  		map[1][0]=2;map[1][4]=4;map[1][5]=6;
  		map[2][0]=3;map[2][3]=2;
  		map[3][0]=6;map[3][2]=2;map[3][4]=1;map[3][5]=3;
  		map[4][1]=4;map[4][3]=1;
  		map[5][1]=6;map[5][3]=3;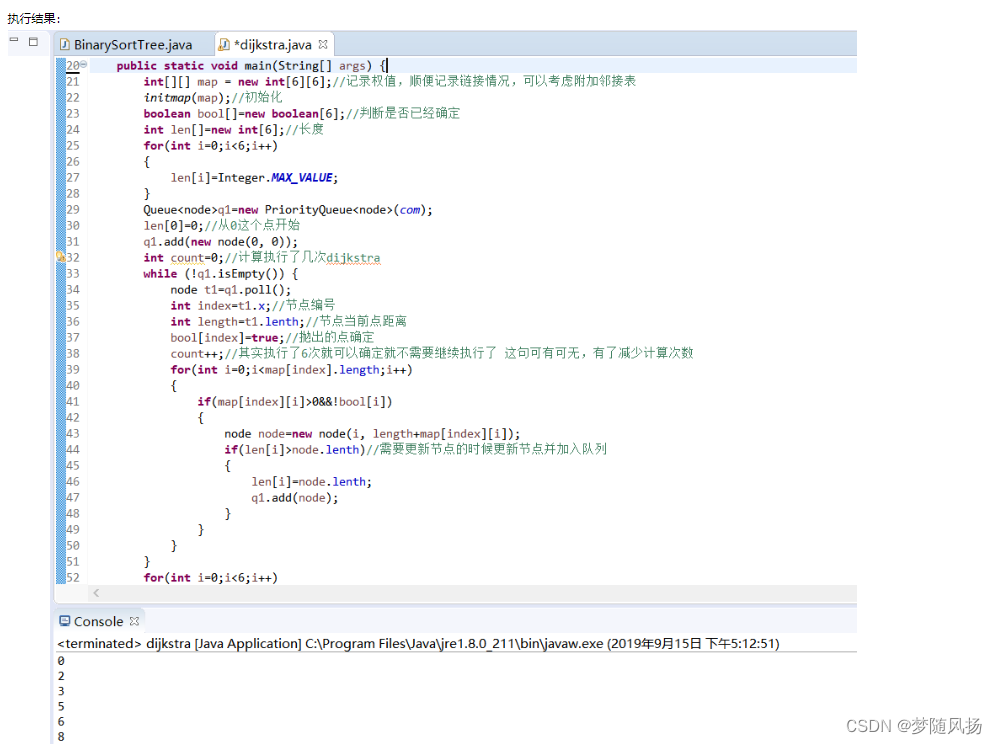	
  	}
  }
  
  
  

  

  ---

  三、如何优化算法才能获得更好的结果呢？你平时是从哪些思路进行优化的？

  1. 算法的优缺点：

    Dijkstra算法适用于以下场景：

  • 寻找两点之间的最短路径。
  • 需要在边权为负数或浮点数的图中计算最短路径。
  • 图中顶点的个数比较小，可以承受O(n^2)的时间复杂度。
  • 不需要考虑负权重的边。
  • 源点和目标点固定，只需要计算它们之间的最短路径。

    Dijkstra算法不适用于以下场景：

  • 图中顶点的个数很大，计算时间会很长。
  • 边权可能为负数或浮点数，需要使用其他算法来处理。
  • 需要考虑负权重的边，可以使用Bellman-Ford算法或Edmonds-Karp算法。
  • 需要同时寻找多个起点到某个定点的最短路径，可以使用Dinic算法。

  2. 算法优化：

  1. 使用最小堆来加速选择当前距离源点最近的未确定节点的过程，可以将堆调整为最大堆以保证最小堆性质。
  2. 对于有负边权或浮点数边权的图，可以使用其他算法来处理，例如Bellman-Ford算法或Edmonds-Karp算法。
  3. 对于稠密图或具有限制的顶点数的图，可以使用Dijkstra算法的变体，例如SPFA算法或A*算法。
  4. 使用并行化技术来加速Dijkstra算法的执行，例如使用多线程或分布式计算技术。
  5. 在实际应用中，可以根据具体情况选择合适的优化方法，例如结合多种算法进行混合优化等。

  ---

  四、在使用算法的过程中需要注意哪些细节才能使其发挥最大的效能呢？

  细节注意：
    以下是使用Dijkstra算法时需要注意的一些细节，以使其发挥最大的效能：

  1. 确定源点和目标点：在使用Dijkstra算法之前，必须先确定源点和目标点。源点表示要计算最短路径的起点，目标点表示要计算最短路径的终点。

  2. 选择合适的数据结构：Dijkstra算法需要使用一个最小堆来存储未确定节点的信息。因此，在实际应用中，需要选择合适的数据结构来存储顶点的信息。常用的数据结构包括数组、链表、二叉堆等。

  3. 初始化dist数组：在使用Dijkstra算法之前，需要对dist数组进行初始化。对于无向图或有向图中的每个顶点i,将dist[i]初始化为无穷大(表示该顶点到源点的距离为无限大)。

  4. 更新dist数组：在更新dist数组时，需要比较与当前节点相邻的所有节点的dist值，并更新距离源点最近的未确定节点的dist值。更新dist值时，需要使用min-heap来保证正确的顺序。

  5. 处理负边权或浮点数边权的情况：如果存在负边权或浮点数边权的情况，需要使用其他算法来处理。例如，可以使用Bellman-Ford算法或Edmonds-Karp算法来处理带负边权或浮点数边权的图。

  6. 避免重复遍历：在更新dist数组的过程中，需要避免重复遍历相同的顶点。为了避免这种情况的发生，可以使用一个哈希表来记录已经遍历过的顶点。

  7. 考虑边界情况：在使用Dijkstra算法时，需要考虑边界情况。例如，当所有顶点的dist值都为无穷大时，表示不存在从源点到目标点的路径；当所有顶点的dist值都相等时，表示存在多条从源点到目标点的路径。

  ---

  
  

  部分参考：
  Dijkstra算法详细(单源最短路径算法)