本文主要记录的是笔者在B站自学Numpy库的学习笔记。
引入numpy库
import numpy as np
矩阵的创建
创建一个二行三列的矩阵。
array = np.array([[1,2,3],
[2,3,4]])
查看array的行数、形状、元素数量
print("number of dim:",array.ndim)
print("shape:",array.shape)
print("size:",array.size)
执行结果:
其中
ndim显示的是它的行数;
shape显示的是它的形状(2行3列的矩阵);
size显示的是它的元素数量(6个)
创建0矩阵
array = np.zeros((4,5)) #4行5列的0矩阵
执行结果:
创建全1矩阵
array = np.ones((4, 5),dtype=int) # 4行5列的全1矩阵并用dtype属性设置成int类型
执行结果:
创建有步长的一维矩阵
array = np.arange(1,22,3) # [1,22)步长为3的一维矩阵
执行结果
用reshape方法创建多维矩阵
array = np.arange(20).reshape((4,5)) # 4行5列0~19的矩阵
执行结果
创建一维序列线段
array = np.linspace(10,30,6) # 一行从10到30,6个步长的序列线段
执行结果
创建多维序列线段
array = np.linspace(10, 30, 6).reshape((3,2)) # 3行2列从10到30,6个步长的序列线段
执行结果
生成多维随机数矩阵
array = np.random.random((3,5)) # 3行5列从0到1的随机数
我们还可以使用numpy内置的一些方法进行数值计算,比如求和、搜索最大值、走索最小值、按行求和、按列求最小值、按行求最大值等等(axis=1时表示横向,axis=0表示纵向)。
np.sum(array) #将元素求和
np.min(array) # 将元素求最小值
np.max(array) # 将元素求最大值
np.sum(array,axis=1) # 按行求和
np.min(array, axis=0) # 按列求最小值
np.max(array, axis=1) # 按行求最大值
执行结果
矩阵相加
矩阵相加,只需要简单的用+号就可以完成。
a = np.array([4,5,6,7,8])
b = np.arange(5)
c = a+b
执行结果
矩阵点乘
矩阵点乘指的是矩阵之间对应位置元素相乘。
用刚才的b矩阵点乘自身。
b = b**2
执行结果
c = np.array([[1,1,1],
[0,1,2],
[2,3,4]])
d = np.arange(9).reshape((3,3))
e = c*d #c矩阵和d矩阵进行点乘
运行结果:
矩阵叉乘
矩阵叉乘就是我们在线性代数里面学的“矩阵乘法”。
叉乘使用的方法是dot()。两种写法:
dot = np.dot(c,d)
dot = c.dot(d)
执行结果:
矩阵的元素布尔判断
判断a矩阵里的元素是否比6大
a > 6
执行结果:
一些常用的运算
例如找最大元素的索引、最小元素索引、计算平均值、计算中位数、计算逐项累加值、计算逐项差值、寻找非0元素下索引、逐行排序、矩阵转置、矩阵自叉乘、按列计算平均值、滤波操作等。
array = np.arange(2, 14).reshape((3, 4))
np.argmax(array) # 最大值索引
np.argmin(array) # 最小值索引
array.mean() # 计算平均值
np.average(array) # 计算平均值
np.median(array) # 计算中位数
pnp.cumsum(array) # 计算逐项累加值
np.diff(array) # 计算逐项差值
np.nonzero(array) # 给出非0元素的下标
np.sort(array) # 逐行排序
np.transpose(array) # 矩阵的转置
array.transpose() # 矩阵的转置
array.T # 矩阵的转置
(array.T).dot(array) # 矩阵转置后叉乘
np.mean(array, axis=0) # 按列计算平均值
np.clip(array, 5, 9) # 滤波,设置小于5的数等于5,大于9的数等于9
运行结果:
关于非0元素下标,输出的是两个一位数组,分别代表非0元素的x轴位置和y轴位置。
矩阵索引
array = np.arange(0,16).reshape((4,4))
array[2] #获取第二行的所有元素
array[2][1] #获取第2行第1列的元素
array[2,1] #也可以这么写
array[:,1] #第1列所有数
array[1, 1:3] # 第1行第1列到第3列之前所有数
array.flatten() #拉平矩阵
运行结果:
矩阵的合并
a = np.array([1,2,3])
b = np.array([4,5,6])
np.vstack((a, b)) # 上下合并 v:vertical
np.hstack((a, b)) # 左右合并 h:horizontal
运行结果
一维矩阵的转置
对单行序列不可以通过转置的方式得到单列的序列,直接写a.T是转置不了a的。通过a.shape可以得到:(3,),说明现在只有一个维度,而转置是两个维度的事情。所以可以通过newaxis的方式添加纵向维度来达到转置的目的。
a[:,np.newaxis] #[横向维度,纵向维度]
如果还要转置回来,a.T可不可以达到目的呢?也不可以。通过a.shape还是会得到:(3,),说明此时a还是被看作是一维的数组。再转置回来怎么办?那就通过添加横向纬度来转置!
a[np.newaxis,:]
运行结果:
矩阵的分割
用split、vsplit、hsplit可以进行等份分割,用array_split可以进行不等份分割
a = np.arange(20).reshape((4, 5))
np.split(a, 5, axis=1) # 分割后成横向排列,也就是对列进行等分分割,分割成5部分
np.split(a, 2, axis=0) # 分割后成纵向排列,也就是对行进行等分分割,分割成2部分
#等效写法:
np.vsplit(a, 2) #等份分割后成纵向
np.hsplit(a, 5) #等份分割后成横向
#不等分划分
np.array_split(a, 3, axis=1) #不等份分割成4份后成横向
运行结果:
“成横向”的意思是分割完毕后每一组是横向摆,同理“成纵向”是分割完毕后每一组是纵向摆。
浅拷贝与深拷贝
假设现在有两个矩阵array1,array2。
浅拷贝的写法是:array2 = array1; 这种写法只是array2对array1的简单引用,也就意味着对array1的属性进行修改时,array2的属性也会跟着变,说白了此时array2就是array1。类似于C语言的地址传递(实参传递)。
深拷贝的写法是:array2 = array1.copy(); 这种写法是将array1的所有属性及参数一并拷贝给array2,但是array2并不对array1进行引用。这也就意味着,array1的属性改变时,不会影响array2的属性。类似于C语言的值传递(形参传递)
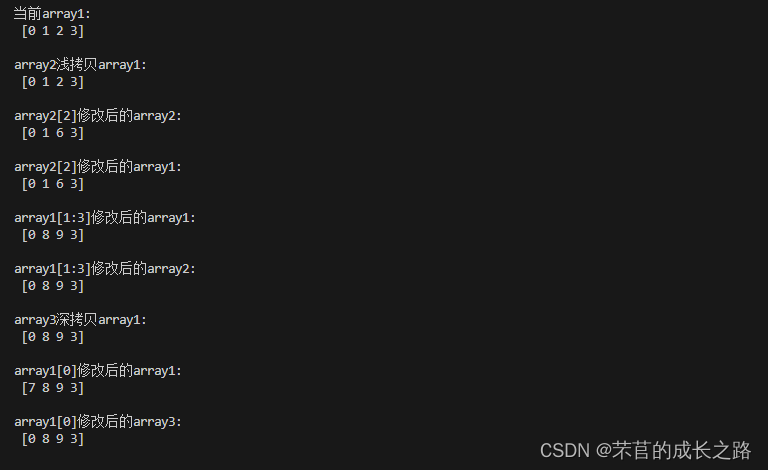
array1 = np.arange(4)
os.system("cls")
print("当前array1:\n",array1,"\n")
array2 = array1 # 浅拷贝。类似于地址传递,实参赋值
print("array2浅拷贝array1:\n",array2,"\n")
array2[2] = 6
print("array2[2]修改后的array2:\n",array2,"\n")
print("array2[2]修改后的array1:\n",array1,"\n") # array2 和 array是同一个东西
array1[1:3] = [8,9]
print("array1[1:3]修改后的array1:\n",array1,"\n")
print("array1[1:3]修改后的array2:\n",array2,"\n")
# 深拷贝
array3 = array1.copy()
print("array3深拷贝array1:\n",array3,"\n")
array1[0] = 7
print("array1[0]修改后的array1:\n",array1,"\n")
print("array1[0]修改后的array3:\n",array3,"\n")
运行结果:
敬请批评指正。