一、A星算法简介

A*算法是一种静态路网中求解最短路径最有效的直接搜索方法，也是解决许多搜索问题的有效算法。算法中的距离估算值与实际值越接近，最终搜索速度越快。
在这里插入图片描述

二、A星算法思想

A星（A-Star)算法是一种静态路网中求解最短路径最有效的直接搜索方法，也是许多其他问题的常用启发式算法。注意——是最有效的直接搜索算法，之后涌现了很多预处理算法（如CH），在线查询效率是A*算法的数千甚至上万倍。

A*算法通过下面这个函数来计算每个节点的优先级， $f (n)$ 越小，状态 $n$ 被选择的优先级就越大：

公式表示为： $f (n) = g (n) + h^{'} (n)$ ,

$f (n)$ 是从初始状态经由状态 $n$ 到目标状态的最小代价估计，
$g (n)$ 是在状态空间中从初始状态到状态 $n$ 的最小代价，
$h^{'} (n)$ 是从状态 $n$ 到目标状态的路径的最小估计代价。（对于路径搜索问题，状态就是图中的节点，代价就是距离）

假设 $h (n)$ 为状态 $n$ 到目标状态的路径的最小真实代价。

则保证找到最短路径（最优解的）条件，关键在于估价函数 $f (n)$ 的选取（或者说 $h^{'} (n)$ 的选取）。

以 $h^{'} (n)$ 表达状态 $n$ 到目标状态估计的距离，那么 $h^{'} (n)$ 的选取大致有如下三种情况：

如果 $h^{'} (n) < h (n)$ ，这种情况下，搜索的点数多，搜索范围大，效率低。但能得到最优解。
如果 $h^{'} (n) = h (n)$ ，此时的搜索效率是最高的。
如果 $h^{'} (n) > h (n)$ ，搜索的点数少，搜索范围小，效率高，但不能保证得到最优解。

三、A星算法 java代码

@Data
public class AStar {
    // 0是路 1是墙 2是起点 3是终点
    private int[][] map;
    // 起点坐标
    int startI;
    int startJ;
    // 终点坐标
    int endI;
    int endJ;

    public AStar(int[][] map) {
        this.map = map;
        // 获取起点和终点坐标
        for (int i = 0; i < map.length; i++) {
            for (int j = 0; j < map[i].length; j++) {
                if(map[i][j]==2){
                    startI = i;
                    startJ = j;
                }
                if(map[i][j]==3){
                    endI = i;
                    endJ = j;
                }
            }
        }
    }

    public void solve(){
        boolean[][] active = new boolean[map.length][map[0].length];
        PriorityBlockingQueue<Node> priorityBlockingQueue = new PriorityBlockingQueue<>();
        // 从起点出发
        ArrayList<int[]> initPath = new ArrayList<>();
        initPath.add(new int[]{startI,startJ});
        priorityBlockingQueue.add(new Node(startI,startJ,initPath,caculateDistance(startI,startJ)));
        active[startJ][startJ] = true;
        // 开始循环
        while (!priorityBlockingQueue.isEmpty()){
            Node node = priorityBlockingQueue.poll();
            if(node.getI()==endI && node.getJ()==endJ){
                for (int[] p : node.getPath()) {
                    System.out.println(Arrays.toString(p));
                }
                System.out.println("最短路长度为："+node.getPath().size());
                break;
            }
            // 向四周进行扩充
            // 上
            int i1 = node.getI()-1;
            int j1 = node.getJ();
            if(isAble(i1,j1,active)){
                ArrayList<int[]> path = new ArrayList<>(node.getPath());
                path.add(new int[]{i1,j1});
                priorityBlockingQueue.add(new Node(i1,j1,path,caculateDistance(i1,j1)));
                active[i1][j1] = true;
            }
            // 下
            int i2 = node.getI()+1;
            int j2 = node.getJ();
            if(isAble(i2,j2,active)){
                ArrayList<int[]> path = new ArrayList<>(node.getPath());
                path.add(new int[]{i2,j2});
                priorityBlockingQueue.add(new Node(i2,j2,path,caculateDistance(i2,j2)));
                active[i2][j2] = true;
            }
            // 左
            int i3 = node.getI();
            int j3 = node.getJ()-1;
            if(isAble(i3,j3,active)){
                ArrayList<int[]> path = new ArrayList<>(node.getPath());
                path.add(new int[]{i3,j3});
                priorityBlockingQueue.add(new Node(i3,j3,path,caculateDistance(i3,j3)));
                active[i3][j3] = true;
            }
            // 右
            int i4 = node.getI();
            int j4 = node.getJ()+1;
            if(isAble(i4,j4,active)){
                ArrayList<int[]> path = new ArrayList<>(node.getPath());
                path.add(new int[]{i4,j4});
                priorityBlockingQueue.add(new Node(i4,j4,path,caculateDistance(i4,j4)));
                active[i4][j4] = true;
            }
        }
    }
    // 判断坐标是否可行
    private boolean isAble(int i,int j,boolean[][] active){
        if(i<0 || i>=map.length){
            return false;
        }
        if(j<0 || j>= map[0].length){
            return false;
        }
        if(map[i][j]==1 || active[i][j]){
            return false;
        }
        return true;
    }
    // 计算距离终点的曼哈顿
    private int caculateDistance(int i,int j){
        return Math.abs(i-endI)+Math.abs(j-endJ);
    }
    @Data
    @NoArgsConstructor
    @AllArgsConstructor
    class Node implements Comparable<Node>{
        int i;
        int j;
        List<int[]> path;
        // 距离终点的曼哈顿距离
        int lenToEnd;
        @Override
        public int compareTo(Node o) {
            return Integer.compare(lenToEnd+path.size(),o.lenToEnd+o.path.size());
        }

        @Override
        public String toString() {
            return "Node{" +
                    "i=" + i +
                    ", j=" + j +
                    ", lenToEnd=" + lenToEnd +
                    '}';
        }
    }
}

四、测试

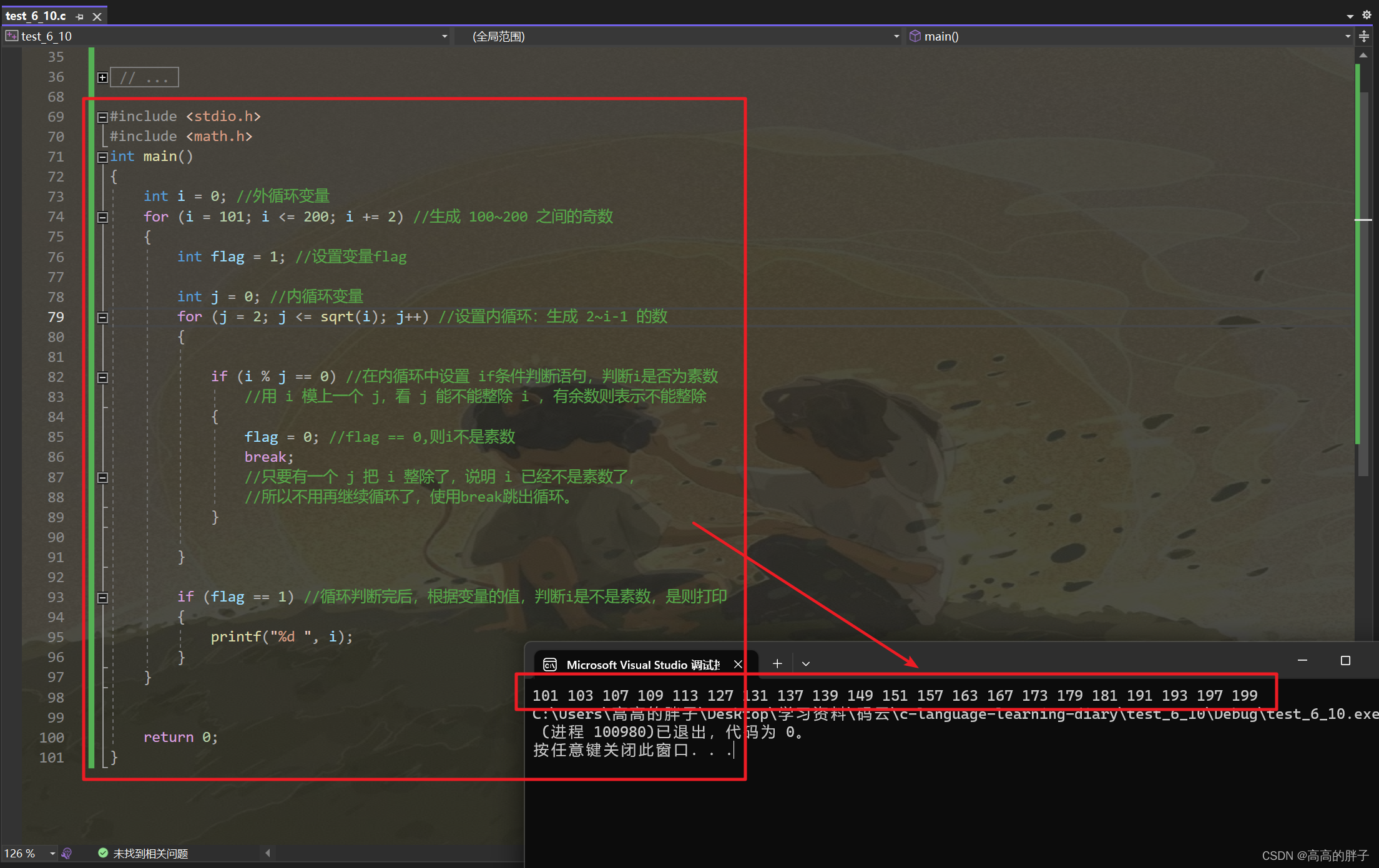
public class Test {
    public static void main(String[] args) {
        long start = System.currentTimeMillis();
        int[][] map = new int[][]{
                {1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0},
                {0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0},
                {0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0},
                {0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0},
                {0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0},
                {0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0},
                {0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0},
                {0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0},
                {0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0},
                {0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0},
                {0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0},
                {0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0},
                {0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0},
                {0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0},
                {0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0},
                {0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1},
                {0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1},
                {0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1},
                {0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1},
                {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 3, 0, 0, 0, 0, 0, 0, 0},
        };
        new AStar(map).solve();
        System.out.println("用时："+(System.currentTimeMillis()-start)+"ms");
    }
}

控制台输出：

[1, 4]
[1, 5]
[1, 6]
[1, 7]
[1, 8]
[1, 9]
[2, 9]
[2, 10]
[2, 11]
[3, 11]
[4, 11]
[5, 11]
[6, 11]
[7, 11]
[8, 11]
[9, 11]
[10, 11]
[10, 12]
[11, 12]
[12, 12]
[12, 11]
[13, 11]
[14, 11]
[15, 11]
[16, 11]
[17, 11]
[17, 12]
[17, 13]
[17, 14]
[18, 14]
[19, 14]
[19, 13]
[19, 12]
最短路长度为：33
用时：6ms