目录
一:树概念及结构
1.树的概念
2.树的相关概念
3.树的表示
二:二叉树的概念及结构
1.概念
2.特殊的二叉树
<1>. 满二叉树:
<2>. 完全二叉树:
3.二叉树的性质
4.二叉树的存储结构
<1>.顺序结构
<2>.链式结构
5.链式二叉树的实现
<1>:二叉树的前序遍历
<2>.二叉树的中序遍历
<3>.二叉树的后序遍历
<4>.二叉树的节点个数
<5>.二叉树的叶子节点的个数
<6>.二叉树的高度
<7>.二叉树第k层节点个数
<8>.二叉树查找值为x的节点
<9>.二叉树销毁
<10>.通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
一:树概念及结构
1.树的概念
2.树的相关概念
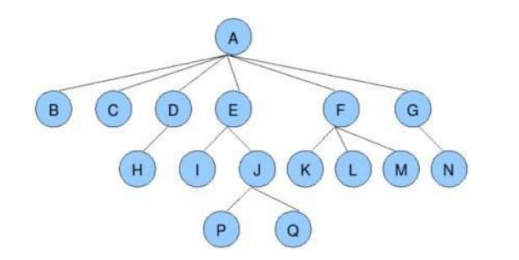
3.树的表示
typedef int DataType;struct Node{struct Node* firstChild; // 第一个孩子结点struct Node* pNextBrother; // 指向其下一个兄弟结点DataType _data; // 结点中的数据域};
画图表示:

二:二叉树的概念及结构
1.概念
2. 由一个根节点加上两棵别称为左子树和右子树的二叉树组成

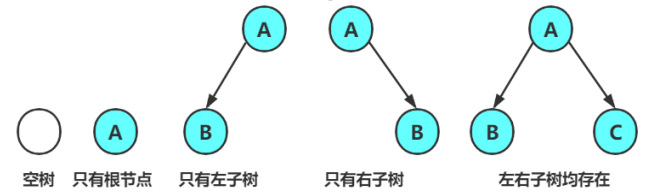
2.特殊的二叉树
<1>. 满二叉树:
一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为H,且结点总数是 2^ H - 1,则它就是满二叉树。

<2>. 完全二叉树:

3.二叉树的性质
2. 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是 2^h - 1。

4.若规定根节点的层数为1,具有n个结点的满二叉树的深度:
h = log2 (n+1) --- 以2为底,n+1的对数。
5.对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的结点有:
<1>. 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
<2>. 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
4.二叉树的存储结构
<1>.顺序结构
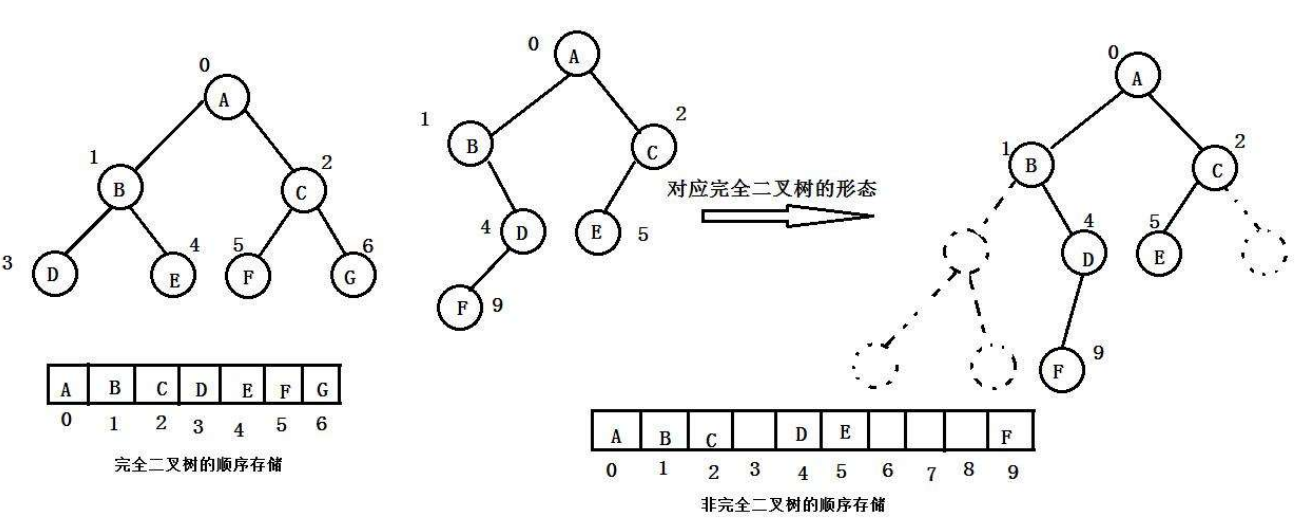
<2>.链式结构
5.链式二叉树的实现
在此处,我们先手动创建一个二叉树,链式二叉树,可以开辟节点,然后自己进行链接:
//链式二叉树
typedef char BTDataType;
typedef struct BinaryTreeNode
{
BTDataType _data;
struct BinaryTreeNode* _left;
struct BinaryTreeNode* _right;
}BTNode;BTNode* BuyNode(BTDataType x)
{
//开辟结点
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL)
{
perror("malloc fail\n");
return NULL;
}
node->_data = x;
node->_left = NULL;
node->_right = NULL;return node;
}
BTNode* CreaBinaryTree()
{
BTNode* node1 = BuyNode('a');
BTNode* node2 = BuyNode('b');
BTNode* node3 = BuyNode('c');
BTNode* node4 = BuyNode('d');
BTNode* node5 = BuyNode('e');
BTNode* node6 = BuyNode('f');
BTNode* node7 = BuyNode('g');
BTNode* node8 = BuyNode('h');//进行链接 --- 二叉树
node1->_left = node2;
node1->_right = node3;
node2->_left = node4;
node2->_right = node5;
node3->_left = node6;
node3->_right = node7;
node4->_left = node8;return node1;
}
<1>:二叉树的前序遍历
前序:根、左子树、右子树
void BinaryTreePrevOrder(BTNode* root);
在自己进行链接时,开辟了:a b c d e f g h 几个节点,其链接后的图形为:
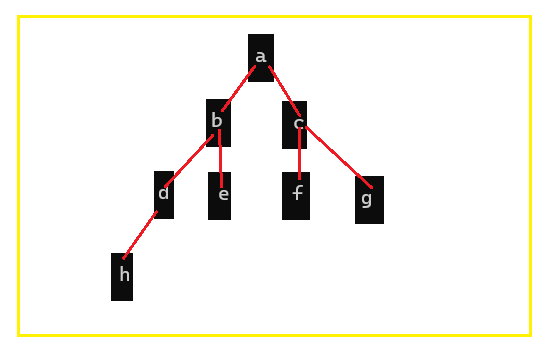
代码为:
// 二叉树前序遍历
//前序遍历 --- 根,左子树,右子树
void BinaryTreePrevOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
printf("%c ", root->_data);
BinaryTreePrevOrder(root->_left);
BinaryTreePrevOrder(root->_right);
}程序运行成功后:

画图验证:

在此处我们仅画出了,左半部分的递归展开图
画到了(a b d h N N N e N N ),右边部分由于空间不够原因,不在展开画出。
<2>.二叉树的中序遍历
中序:左子树、根、右子树
void BinaryTreeInOrder(BTNode* root);
代码为:
// 二叉树中序遍历
//中序遍历 --- 左子树,根,右子树
void BinaryTreeInOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
BinaryTreeInOrder(root->_left);
printf("%c ", root->_data);
BinaryTreeInOrder(root->_right);
}
运行效果为:
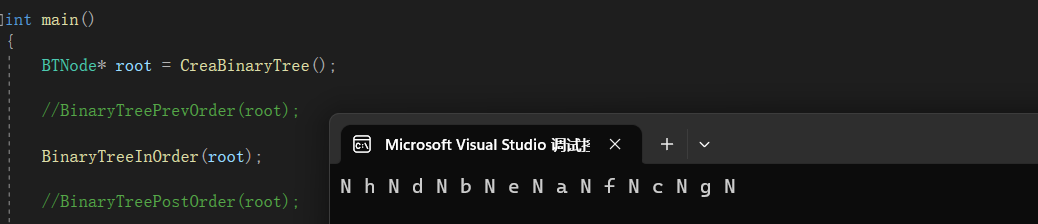
画递归展开图表示:

<3>.二叉树的后序遍历
后序:左子树、右子树、根
void BinaryTreePostOrder(BTNode* root);
代码为:
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
BinaryTreeInOrder(root->_left);
BinaryTreeInOrder(root->_right);
printf("%c ", root->_data);
}
运行效果为:
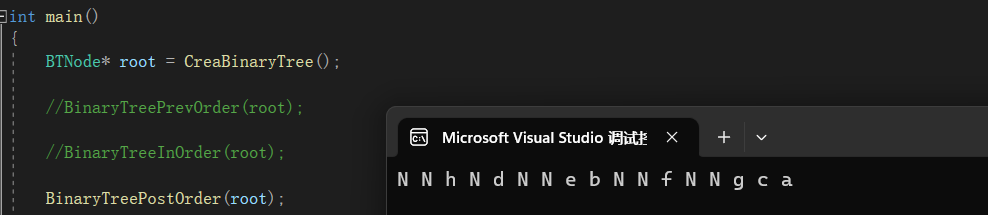 画递归展开图表示:
画递归展开图表示:
 尝试画简单的递归展开图 --- 在二叉树上画图表示出来:
尝试画简单的递归展开图 --- 在二叉树上画图表示出来:

<4>.二叉树的节点个数
void BinaryTreeSize(BTNode* root);
若节点为空,则返回0。
否则,返回左子树的节点个数 + 右子树的节点个数 + 1
代码为:
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
return BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1;
}
运行效果为:
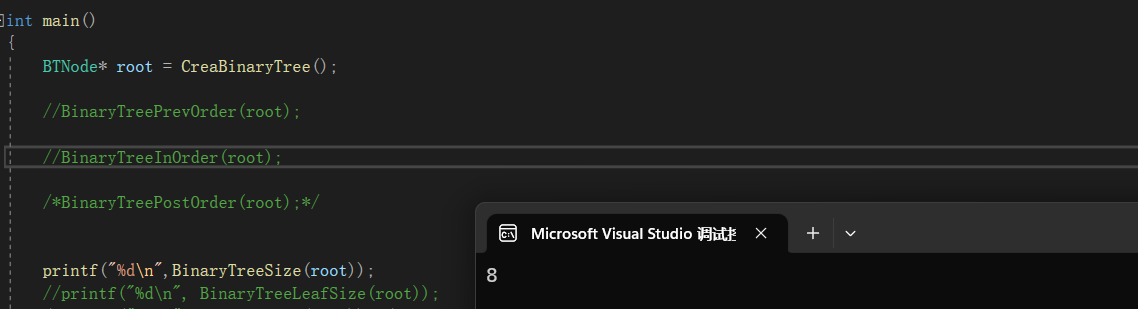
画函数递归展开图:
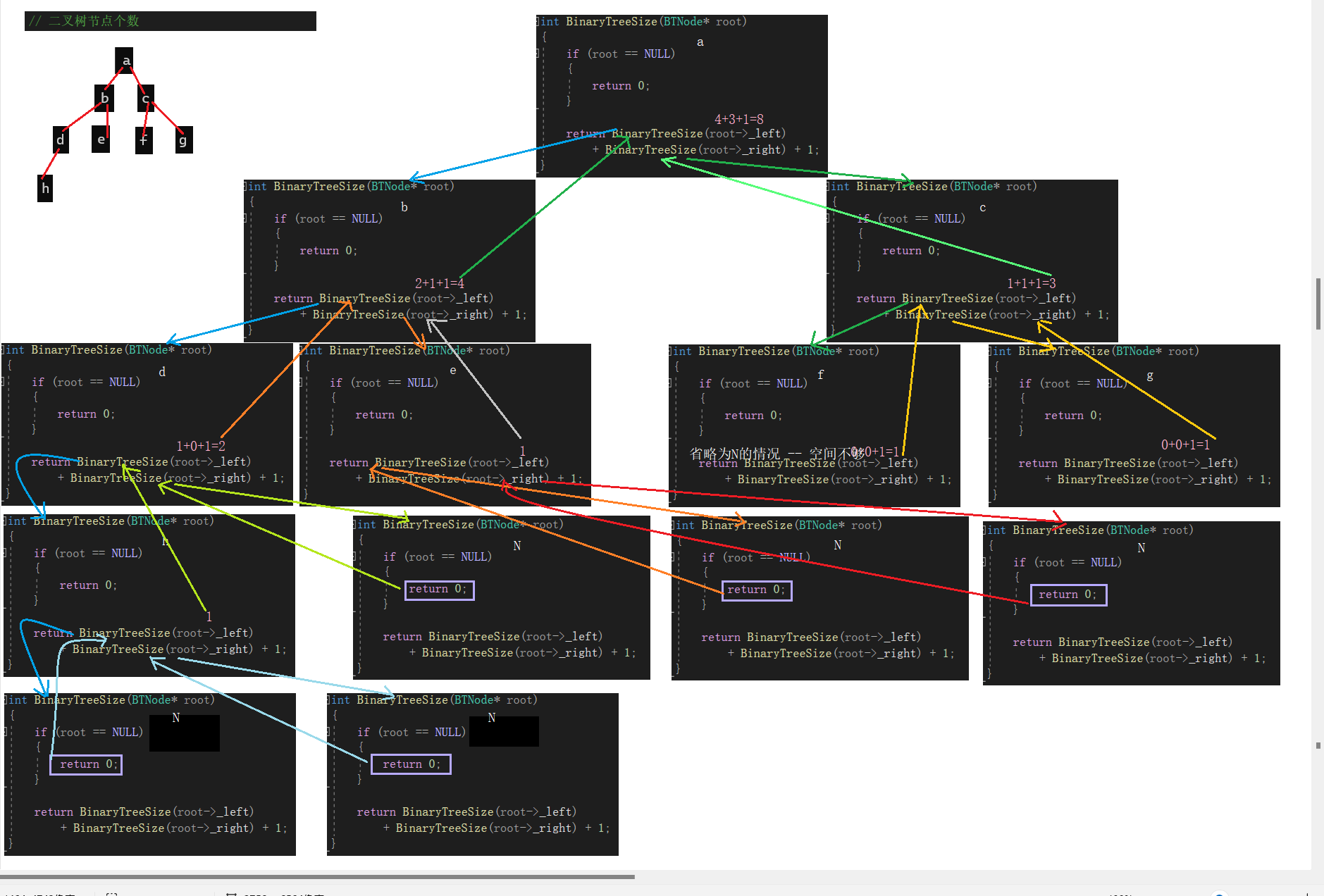
<5>.二叉树的叶子节点的个数
叶子节点 --- 度为 0 的节点。
void BinaryTreeLeafSize(BTNode* root);
若节点为空,则返回 0 ;
若节点的( 左/右 )节点都为空,即该节点的度为 0 ,为叶子节点,返回1;
然后计算左子树和右子树的叶子节点个数。
代码为:
// 二叉树叶子节点个数
//叶子节点 --- 度为0的节点
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->_left == NULL && root->_right == NULL)
{
return 1;
}
return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}
运行效果为:
根据构建的 二叉树可知,该二叉树的叶子节点为 4
<6>.二叉树的高度
int BTreeHeight(BTNode* root);
//存在领导不记事的情况
代码为:
//二叉树的高度
int BTreeHeight(BTNode* root)
{
if (root == NULL)
{
return 0;
}
//领导不记事,当树特别大的时候,会超出时间限制。 --- 应将所得数据保存下来
//return BTreeHeight(root->_left) > BTreeHeight(root->_right) ? BTreeHeight(root->_left) + 1 : BTreeHeight(root->_right) + 1;
int LeftHeight = BTreeHeight(root->_left);
int RightHeight = BTreeHeight(root->_right);
return LeftHeight > RightHeight ? LeftHeight + 1 : RightHeight + 1;
//加1加的是根节点
}
运行效果为:
通过观察可以得知,我们所创建的二叉树为4层,故二叉树的高度为4。
<7>.二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
//我们需要通过第 k - 1 层,来判定第 k 层
代码为:
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
assert(k>0);// k 值必须为大于0的有效值
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
return BinaryTreeLevelKSize(root->_left, k - 1)
+ BinaryTreeLevelKSize(root->_right, k - 1);
}
运行效果为:

第三层有四个
第四层有一个
画递归展开图进行分析:

<8>.二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
代码为:
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->_data == x)
{
return root;
}
BTNode* ret1 = BinaryTreeFind(root->_left, x);
if (ret1)
{
return ret1;
}
BTNode* ret2 = BinaryTreeFind(root->_right, x);
if (ret2)
{
return ret2;
}
return NULL;
}运行效果为:
---- 可以找到的情况
---- 不可以找到的情况
<9>.二叉树销毁
void BinaryTreeDestory(BTNode** root);
代码为:
// 二叉树销毁
void BinaryTreeDestory(BTNode** root)
{
if ((*root) == NULL)
{
return;
}
BinaryTreeDestory(&(*root)->_left);//BTNode ** root
BinaryTreeDestory(&(*root)->_right);
free(*root);
//在此处进行置空(NULL),对外面没有作用
//可以自己在函数调用后进行置空操作
}
运行结果为:
---- 程序正确结束
<10>.通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int* pi);
// pi --- 数组下标
//若 a[*pi] == '#' ,数组下标 + 1 ,并且返回空
代码为:
BTNode* BinaryTreeCreate(BTDataType* a, int* pi)
{
if (a[*pi] == '#')
{
(*pi)++;//数组下标 +1
return NULL;
}
BTNode* root = BuyNode(a[*pi]);//开辟节点
(*pi)++;
//进行链接
root->_left = BinaryTreeCreate(a, pi);
root->_right = BinaryTreeCreate(a, pi);
return root;
}运行效果为:
画图表示:
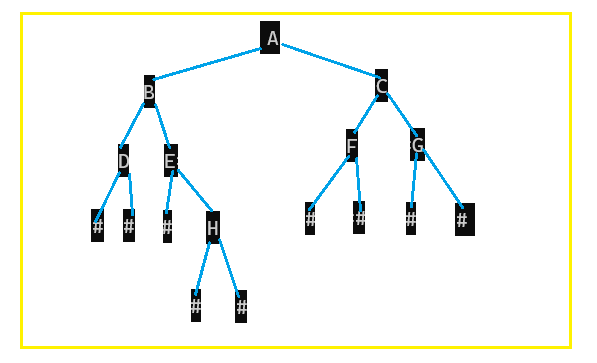









![[NOI2007] 调兵遣将](https://img-blog.csdnimg.cn/4a9c1eda6c3e4d878403bb2fa8d31c02.png)

