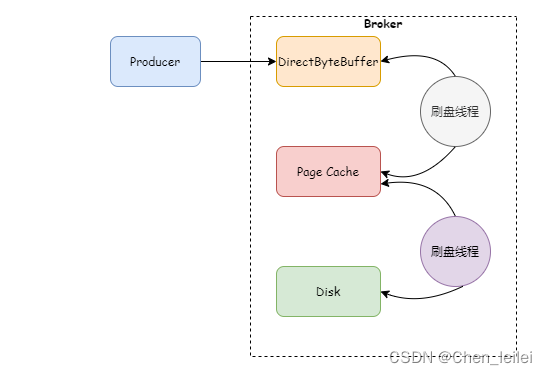
水中声源级SL的求解应用举例

在水声学中，经常会遇到声源级的概念，并根据声源级的大小估计其他重要参数，本文举例说明声源级的概念和定义。
一、声源级的定义
声源级用来描述声音辐射源所产生声信号或噪声在1m距离处的声强量级。其定义为
$$SL=10{\log }_{10}(\frac{I_{1m}}{I_{ref}})$$
其中，水中$I_{ref}\approx 0.67\times 10^{-18}W/{\mathrm{m}}^2$

图1 声源辐射声音示意图

二、举例
假设点声源发射功率为$P_a$=450W，求解它的声源级$SL$是多少？
解答:
根据声源级的定义可知：声源级用来描述声音辐射源所产生声信号或噪声在1m距离处的声强量级。其定义为
$$SL=10{\log }_{10}(\frac{I_{1m}}{I_{ref}})\dots \dots \dots \dots （1）$$
其中，水中$I_{ref}\approx 0.67\times 10^{-18}W/{\mathrm{m}}^2$.
若声音辐射源为点声源，根据声强的计算公式可知:

$$I_{1m}=\frac{P_a}{S_{球}}=\frac{P_a}{4\pi \times 1^2}=\frac{450}{4\pi }=35.8099(W/m^2)\dots \dots \dots \dots （2）$$
将式(2)带入式(1)可得:
$$\begin{array}{l}SL=10{\log }_{10}(\frac{I_{1m}}{I_{ref}})\\ =10{\log }_{10}(\frac{35.8099(W/m^2)}{0.67\times {10}^{-18}(W/m^2)})\\ =10{\log }_{10}(53.4476\times 10^{18})\\ =180+10{\log }_{10}(53.4476)\\ =180+10\times 1.7279\\ =197.279(\mathrm{dB})\end{array}$$
因此，点声源发射功率为$P_a$=450W，它的声源级$SL$=192.279 dB.