板块：基础算法、线性优化
难度：较易
前置知识：C++基础语法

一、前缀和

1、定义

• 在一维空间中，对于一个数据总量为 $n$ 的数组 $a$，有数据 $a[1],a[2],a[3],...,a[n-1],a[n]$，定义一个数组 $sum$，$sum[i]$ 存储 $a[1]\sim a[i]$ 的数据总和，我们就称 $sum$ 是 $a$ 的前缀和.

2.本质与应用领域

对于数组：

1	2	3	4	5	6	7

根据定义，我们计算出它各项所对应的前缀和应该是：

1	3	6	10	15	21	28
1	1+2	3+3	6+4	10+5	15+6	21+7

不难发现，前缀和的本质就是 递推.从前往后依次计算出前缀和.前缀和是一种思想，它是一种对算法进行时间优化的预处理数据的思想.前缀和的应用领域很宽广，比如用于线性优化、求和、预处理数据等.

3.一维前缀和

上文中我们所举的数组便是典型的一维前缀和，其 预处理递推公式 为：$$f[n]=f[n-1]+a[n](n\ge 1,f[0]=0)$$
易得其时间复杂度为 $O(n)$.
完成预处理后，我们将会面临 查询 的问题，对于一个区间 $l\sim r$，查询其区间前缀和的公式为：
$$s[r]-s[l-1](l\ge 1)$$
易得其时间复杂度为 $O(1)$.

4.二维前缀和

二维前缀和和一维前缀和同理，需要推导出预处理递推公式和查询公式.
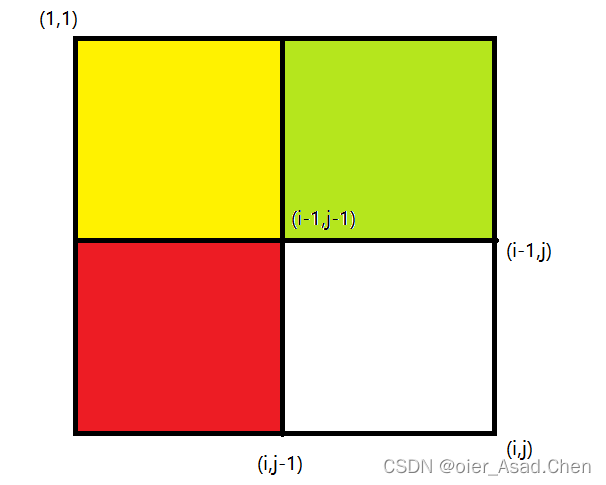
如下图，我们需要递推 $a[1][1]\sim a[i][j]$ 的前缀和即 $s[i][j]$ .由图示可知，$s[i][j-1]$ 存储的是 $a[1][1]\sim a[i][j-1]$ 的前缀和，即黄色区域和红色区域；$s[i-1][j]$ 存储的是 $a[1][1]\sim a[i-1][j]$ 的前缀和，即黄色区域和红色区域.这个推导类似于在电脑中进行框选操作时拖动鼠标的而显示出的矩形区域.如果我们将 $s[i][j-1]$ 和 $s[i-1][j]$ 相加，我们不难得到绿色区域、红色区域和两个黄色区域的前缀和，也就发现多出了一个黄色区域，因此减去 $s[i-1][j-1]$ 即可，然后再加上 $a[i][j]$，也就得到了 $a[1][1]\sim a[i][j]$ 的前缀和.综上分析，我们可以得到二维前缀和的 预处理递推公式 为：
$$s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j]$$

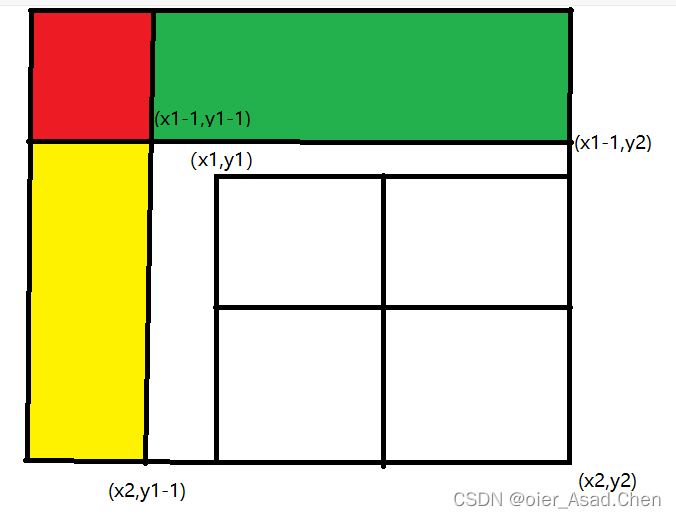
要求以 $(x_1,y_1)$ 为左上端点， $(x_2,y_2)$ 为右下端点的子矩阵的和，我们可以从推导预处理公式的过程中得到启发.$s[x_1-1][y_2]$ 存储的是 $a[1][1]\sim a[x_1-1][y_2]$ 的前缀和，即红色区域和绿色区域； $s[x_2][y_1-1]$ 存储的是 $a[1][1]\sim a[x_2][y_1-1]$ 的前缀和，即红色区域和黄色区域.借鉴推导一维前缀和查询公式时的思路，如果我们用 $s[x_2][y_2]$ 减去 $s[x_1-1][y_2]$ 和 $s[x_2][y_1-1]$ 的和，再加上多减的一个红色区域也就是 $s[x_1-1][y_1-1]$，就可以得到 $s[x_1][y_1]\sim s[x_2][y_2]$ 的总和.综上分析，可以得到二维前缀和的查询公式是：
$$s[x_2][y_2]-s[x_2][y_1-1]-s[x_1-1][y2]+s[x_1][y_1]$$

二、差分

1.定义

在一维空间中，对于一个数据总量为 $n$ 的数组 $a$，有数据 $a[1],a[2],a[3],...,a[n]$，构造一个数组 $b$，有数据为 $b[1],b[2],b[3],...,b[n]$，使得 $a[i]$ 是 $b[1]\sim b[i]$ 的前缀和，我们就称 $b$ 是 $a$ 的差分.例如：

a	1	2	3	4	5
b	1	1	1	1	1

2.实质

通过定义，我们可以知道：我们要想求 $b[i]$，那么就是计算 $a[i]-a[i-1]$，因为 $b$ 是 $a$ 的差分，$a$ 是 $b$ 的前缀和.由此我们可以知道，差分是前缀和的逆运算.

3.一维差分

以 AcWing797.差分 一题为例，如果我们想要让 $a[l]\sim a[r]$ 都加上 $c$，可以采用循环的方式，但是这样的话，其时间复杂度为 $O(nm)$.

如何优化呢？借鉴前缀和的思想，对于区间操作，我们可以让 $a[l]$ 加上 $c$，按照前缀和的思维，让 $a[l]\sim a[n]$ 都加上了 $c$；再让 $a[r+1]$ 减去 $c$，按照前缀和的思维 $a[r+1]\sim a[n]$ 都减去了 $c$，这样的话，就满足了题目要求.

但问题来了，显然在上述分析中，我们只是设想利用前缀和思维，但实际上我们显然不能够直接对 $a$ 数组进行这样的操作再求前缀和，这样的话我们得到的就是 原数组的前缀和数组，而不是原始数组操作后的结果.为了解决这样的问题，差分 就派上用场了.我们可以先构造原数组 $a$ 的差分数组 $b$，先对 $b$ 进行上文中的操作，即若需要让 $a[l]\sim a[r]$ 都加上 $c$，就先让 $b[l]$ 加上 $c$，再让 $b[r+1]$ 减去 $c$，最后对 $b$ 求取前缀和，就得到了 原数组 $a$ 操作后的数组，且保证了是在原数组上进行的操作.这就体现了差分是前缀和的逆运算、对原数组的差分数组求取前缀和就是原数组.

综上，解决原题的关键操作代码就是：

void insert(int l, int r, int c) {
    b[l] += c;
    b[r + 1] -= c;
}

但还有一个问题，在执行插入操作前如何构造差分数组呢？根据前文中差分数组的定义和实质分析，构造原数组的差分数组，就是让 $b[i]$ 加上 $a[i]$， 让 $b[i+1]$ 减去 $a[i]$，就构造了 $a$ 的差分数组 $b$；当然也可以直接使用公式 $b[i]=a[i]-a[i-1]$.

最后对 $b$ 数组求取前缀和，得到答案.

4.二维差分

二维差分可以类比于一维差分，即对一个前缀和的差分.以AcWing.797 二维差分为例.给定以 $(x_1,y_1)$ 为左上端点，以 $(x_2,y_2)$ 为右下端点的子矩阵，将 $a$ 所对应的差分数组 $b$进行如下操作：将 $b[x_1][y_1]$ 加上 $c$，这样就使 $a[x_1][y_1]\sim a[n][m]$ 都加上了 $c$，再迁移推导二维前缀和查询公式时的思维，将 $b[x_1][y_2+1]、b[x_2+1][y_1]$ 减去 $c$， 再对多减的 $b[x_2+1][y_2+1]$ 加上 $c$， 便完成了对于该子矩阵的操作.

同样的，我们也需要在操作前先构造差分数组，我们依然可以选用顺着一维差分的思维，选用公式或利用插入操作.

• 公式：$b[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1]$
• 插入操作，按照上述对子矩阵的操作思路，进行如下操作：

insert(i, j, i, j, a[i][j]);

最后，再对 $b$ 数组进行二维前缀和的求取即为答案.