目录
1.题目描述
2.普通解法(通过部分测试用例)
编辑
3.动态规划解法
3.题目总结
1.题目描述
一个有名的按摩师会收到源源不断的预约请求,每个预约都可以选择接或不接。在每次预约服务之间要有休息时间,因此她不能接受相邻的预约。给定一个预约请求序列,替按摩师找到最优的预约集合(总预约时间最长),返回总的分钟数。
注意:本题相对原题稍作改动
示例 1:
输入: [1,2,3,1]
输出: 4
解释: 选择 1 号预约和 3 号预约,总时长 = 1 + 3 = 4。
示例 2:
输入: [2,7,9,3,1]
输出: 12
解释: 选择 1 号预约、 3 号预约和 5 号预约,总时长 = 2 + 9 + 1 = 12。
示例 3:
输入: [2,1,4,5,3,1,1,3]
输出: 12
解释: 选择 1 号预约、 3 号预约、 5 号预约和 8 号预约,总时长 = 2 + 4 + 3 + 3 = 12。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/the-masseuse-lcci
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
2.普通解法(通过部分测试用例)
class Solution:
def massage(self, nums: List[int]) -> int:
sum = 0
for i in range(len(nums)):
tmp = 0
for j in range(i, len(nums), 2):
tmp += nums[j]
if sum<tmp:
t = tmp
tmp = sum
sum = t
return sum
3.动态规划解法
from typing import List
class Solution:
def massage(self, nums: List[int]) -> int:
cur, prev = 0, 0
for num in nums:
cur, prev = max(prev + num, cur), cur
return curfrom typing import List
class Solution:
def massage(self, nums: List[int]) -> int:
# 初始化当前最大值cur和前一个最大值prev
cur, prev = 0, 0
# 遍历数组
for num in nums:
# 计算当前最大值cur,选择第i个数或不选择第i个数
cur, prev = max(prev + num, cur), cur
# 上一次的最大值prev变成当前最大值cur
# 上一次的次大值cur变成当前最大值的前一个最大值prev
# 返回最终结果cur
return cur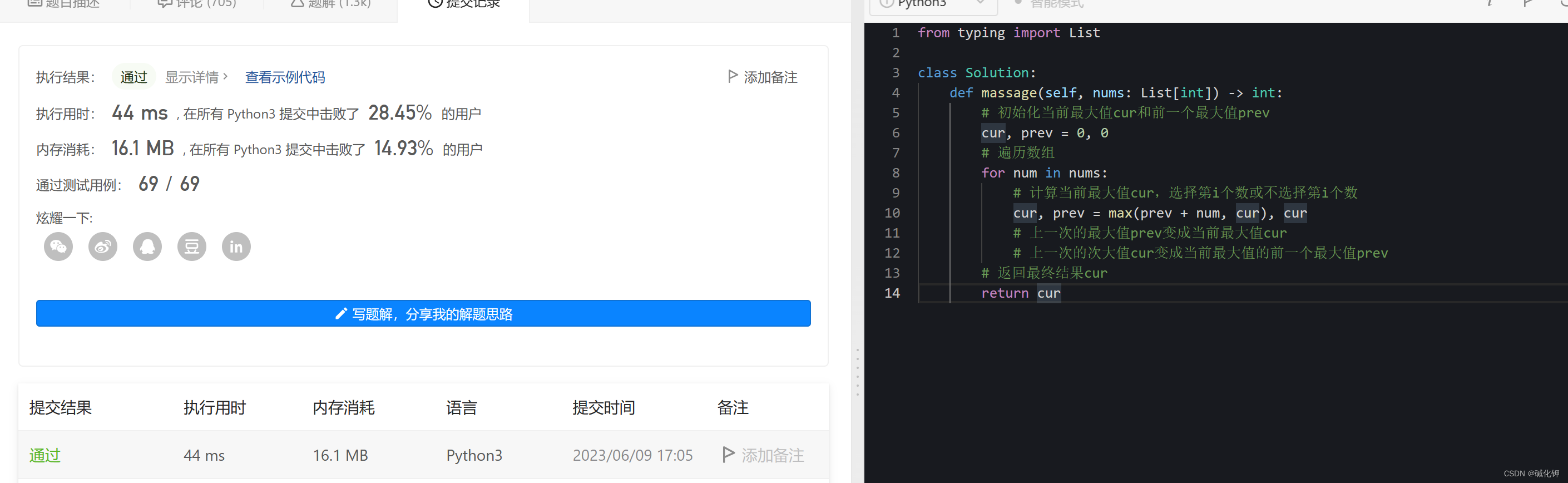
3.题目总结
时间复杂度:O(n),其中n为数组的长度。
空间复杂度:O(1),只需要常数级别的空间来存储当前最大值和前一个最大值。
算法思路:
1.定义状态:
dp[i]表示前i个数中选择不相邻的数所能得到的最大和。
2.状态转移方程:
对于第i个数,有两种情况,选择或不选择。如果选择第i个数,则不能选择第i-1个数,所以dp[i] = dp[i-2] + nums[i]。如果不选择第i个数,则dp[i] = dp[i-1]。
综合两种情况,可以得到状态转移方程:dp[i] = max(dp[i-2] + nums[i], dp[i-1])。 3.边界条件:dp[0] = 0,dp[1] = nums[0]。
4.最终结果:dp[n],其中n为数组的长度。