有穷自动机(FA)对有限存储量设备是比较好的模型，下推自动机对无限存储设备是较好的模型（但是其存储只能用后进先出的栈模式来使用。）这两个模型过于局限，不能作为通用模型。

图灵机

和FA相似，但是图灵机有无限的存储。图灵机可以作实际计算机做的所有事情。但是也有图灵机解不了的事情（这些问题就超越了计算的理论极限。）

图灵机模型使用无限长度的纸带作为无限存储，并且它具有可以读取，写入和移动磁带的读/写头。

开始时，纸带上只有输入字符串，纸带的其他部分都是空的。图灵机有读写头，可以在带子上左右移动。如果需要保存信息，它可能会将该信息写入纸带。要阅读书面消息，它可能会将读/写头移回消息所在的纸带位置。

机器不断计算，直到产生输出。机器事先设置为两种状态：接受或拒绝。如果进入这些状态中的任何一种，则会产生输出接受或拒绝。如果未进入任何接受或拒绝状态，则执行将继续且永不停止。

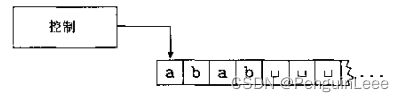
有穷自动机(FA)和图灵机的区别：

1. 图灵机的带子可以写也可以读
2. 读写头可以左右移动
3. 带子无限长
4. 在状态处于接受和拒绝时将立即停机

图灵机的形式定义

图灵机的输入是有限长的。

图灵机在很多情况下是“针对某个算法的”图灵机。根据问题和算法的不同，会出现解决各种问题的图灵机。

这里的算法，意味着状态转移函数$\delta$的不同。

状态转移函数$\delta$是映射：
（当前状态，纸带当前位置字母）$\to$ （下一个状态，纸带字母改写结果，读写头移动方向）

图灵机的格局：包括现在读写头的位置、当前的状态、当前纸带的内容。

我们可以基于格局对图灵机的计算进行形式化。如果图灵机可以合法地从格局C1一步到格局C2，则称格局C1产生格局C2。

起始格局（读写头在纸带最左端）、接受格局（接受状态）、拒绝格局（拒绝状态）。

图灵机M接受的所有字符串全体成为M的语言，记为L(M)。

定义： 如有图灵机识别（接受）一个语言，那么称此语言是图灵可识别的。

图灵机在跑的时候，可能在有限步后接受或者拒绝，也可能无限地运行下去而不停机（称为循环，但是和for/while之类的循环不同，它只是不停机）

于是我们更喜欢对所有输入都停机的图灵机，称其为判定器（不会陷入循环的图灵机）。

定义： 语言是可判定的，如果有图灵机判定它。

可判定 => 可识别，但是可识别不一定意味着可判定。

可判定和可识别性的区别。比如，给定一个单变量多项式$p$，计算它有无整数根。那么图灵机可依次考察0,1,-1,2,-2,…来找整数根。这意味着，它确实可以识别出整数根，但是没有整数根的话，这个算法就得无休无止地跑。

图灵机的变形

1. 多带图灵机：有多个带子，每个带子有自己的读写头。起始输入在第一个带子上。可以通过对纸带进行映射完成等价性证明。
2. 非确定性图灵机：可以类比DFA和NFA。等价性的证明可以考虑对格局变化的广度优先搜索。
3. 枚举器：带有打印机的图灵机。枚举器就是不断地输出语言中的所有串。

计算模型之间的普遍等价性

无限制访问无限的存储器，有这个特点的模型在计算能力上都是等价的，只需要满足一些合理的必要条件。

什么是算法：Church - Turing 论题

这两个人给出了算法的定义。其中，Church给出了$\lambda$演算方法，Turing给出了图灵机。这两个定义是等价的。

在接下来的内容中，我们不去思考图灵机的基本构建，可以直接认为算法能用图灵机实现。

算法的可判定性问题

可判定语言

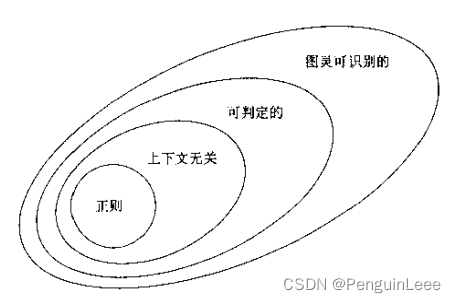
停机问题

有一些问题是计算机不能解（不可判定）的。

典型的例子是：给定一个图灵机和一个串，判断图灵机是否接受这个串。这个问题是不可判定的。

首先，这个问题是可以识别的。我们只需要模拟这个图灵机的状态演变。
这么做的话，确实可以把接受、拒绝态完成。问题是，如果进入循环，他就不停机了。如果它知道自己不停机，那么它可以拒绝串。问题是它不知道。

这样的模拟用图灵机称为通用图灵机，可以模拟任何其他图灵机的行为。

集合的势（元素个数）

对于有限元素的集合，很容易判断他们的元素个数（称为势）是否相等。显然，3元素集的元素个数小于5元素集。

对于无限元素集，通过能否构造双射判断是否等势。

比如，整数集和有理数集等势，记其势为${\aleph }_0$。

实数集和有理数集不等势，记其势为$\aleph$。

$2^{{\aleph }_0}=\aleph$。其证明思路是考虑区间[0,1)中所有数的二进制编码。

通过幂的构造方式，可以证明没有最大的势。此即，假设集合A的势为$c$，则$2^c>c$。

推论： 存在语言不是图灵可识别的。

证明. 所有图灵机构成的集合是可数的。
或者可以考虑给图灵机进行序列化，具体地，对七元组里的东西进行序列化，可以得到图灵机的编码（有限长度编码）。它是二进制自然数的子集。

但是，语言数是不可数的，因为$2^{{\aleph }_0}=\aleph$。

停机问题是不可判定的

首先，定义停机问题
A T M = { < M , w > ∣ M 为图灵机， M 接受 w } A_{TM} = \{<M, w> | M为图灵机，M接受w\} ATM​={<M,w>∣M为图灵机，M接受w}
其中，$<>$代表某种编码。

这个问题是不可判定的。

证明 假设可判定，则存在图灵机$H$可以判定$A_{TM}$。此即
$H(<M,w>)=accept，M$ accepts $w$
$H(<M,w>)=reject，M$ rejects $w$

构造一个新的图灵机$D$，它包含了$H$的逻辑。具体地，$D$的输入为图灵机的编码$<M>$。
$D(<M>)=accept$, if $H(<M,<M>>)=reject$
$D(<M>)=reject$, if $H(<M,<M>>)=accept$

于是当M=D时即为矛盾。

注. 这个做法就像罗素的理发师悖论。理发师说：“我给且仅给不给自己理发的人理发”。于是这个理发师如果不给自己理发，那么他就给自己理发。如果他给自己理发，那么他不给自己理发。

一个图灵不可识别语言

**定理. **一个语言是可判定的，当且仅当它是图灵可识别的，也是补图灵可识别的（补集也是图灵可识别的）。

这就把所有循环的情况排除掉了。证明思路是，考虑用两个图灵机并行地判定语言集和其补。

于是，停机问题的补不是图灵可识别的。

可归约性

略，准备看看P和NP问题之后再回来补…