非线性规划求解方法:序列线性规划(Sequential linear programming)

news2024/11/25 4:44:47

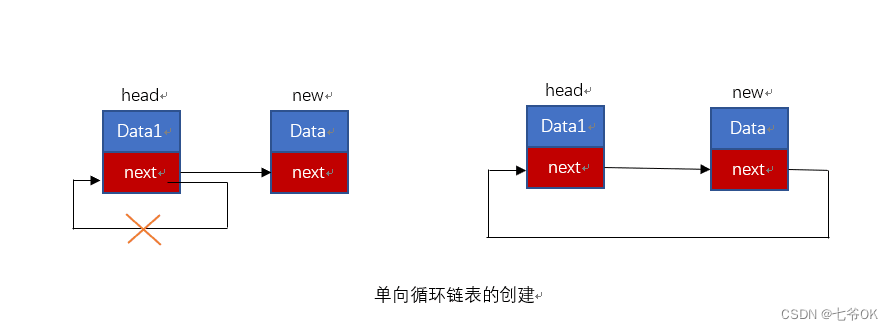
来源：Cornell University Computational Optimization Open Textbook：SLP

1.介绍

2.理论和方法

2.1 问题形式

2.1.1 NLP问题形式

2.1.2 SLP问题形式

2.2 步长边界 Step Bounds

2.3 完整的SLP算法

3.案例

3.1 example1

3.2 example2

4.应用

1.介绍

Sequential linear programming (SLP)序列线性规划也叫successive linear programming，是一个用于解决非线性规划问题non-linear programming (NLP)的数学规划方法。SLP能通过泰勒级数展开将NLP转化为一系列线性规划问题linear programming（LP)，LP可以通过单纯形法或求解器求得解。SLP 最早被称为近似规划法approximation programming，由Shell Oil Company的 R. Griffith 和 R. Stewart 于 1961 年开发。SLP可以在不使用通常昂贵的 NLP 求解器且不使用高阶信息的情况下解决 NLP 问题。SLP不一定是最快的NLP求解算法，在 1994 年的 79 个设计问题的集合中，它的性能与带移动渐近线moving asymptotes的凸近似方法convex approximation差不多，比 CONLIN （一个基于凸近似的对偶优化器）差。但它只需使用LP求解器，从成本效益来看更优越，因此至今仍在使用。

2.理论和方法

2.1 问题形式

2.1.1 NLP问题形式

一个通用的NLP问题形式如下， $x=\left [ x_{1},x_{2},..., x_{n}\right ]$ 是决策变量，f(x)是目标函数，要求最小化，g(x)和h(x)为约束，x取值有上下界。

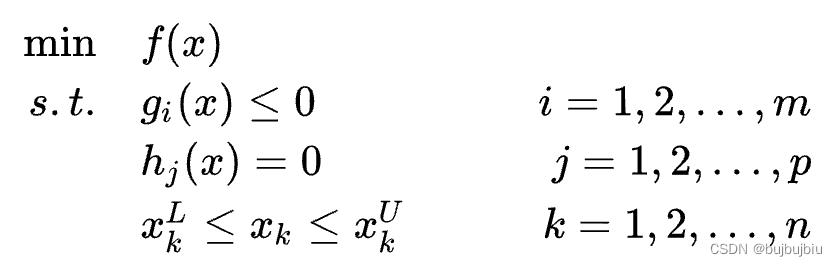
2.1.2 SLP问题形式

将NLP问题中的所有约束和目标函数用在点 $x^{a}$ 处的一阶泰勒展开式代替，转换成SLP问题。这要求 NLP 问题中的函数必须是可微的，SLP 算法才能工作。求解SLP问题获得一个新解 $x^{a+1}$ ，这个新解可能是 NLP 的不可行解，但是不可行的程度会随着迭代次数的增加而降低。

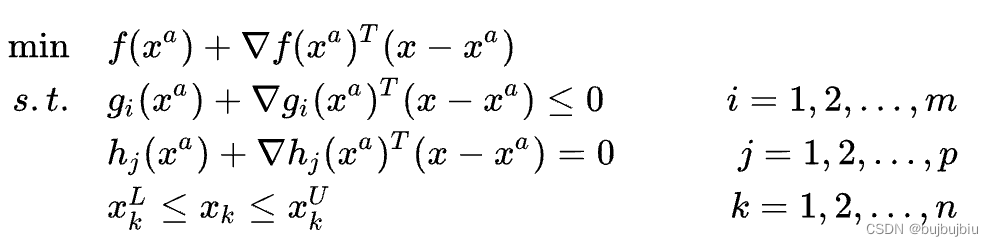
如果NLP的最优解是可行域的一个顶点，那么SLP就会收敛。但是通常情况下不能保证 SLP 会收敛，因为它没有考虑超基本变量superbasic variables，因此在具有许多超基本变量的问题或最优解不在顶点的问题上表现不佳。

超基本变量（superbasic variables）是线性规划中的一个概念，用于描述最优解中的变量状态。在线性规划问题最优解中，有些变量取值是非零的，被称为基本变量（basic variables），而另一些变量的取值为零，则被称为非基本变量（nonbasic variables）。超基本变量是非基本变量中具有潜在优化机会的变量。换句话说，超基本变量是非基本变量中可以通过改变其取值来改善目标函数值的变量。通过将超基本变量移动到基本变量集合中，可以找到更优的解。

为了实现带超基本变量问题的收敛，引入了步长边界step bounds方法

2.2 步长边界 Step Bounds

点 $x^{a}$ 处的一阶泰勒展开式和原来的非线性函数之间误差会随着 $x^{a}$ 和某点 $x^{k}$ 距离增加而增加，因此需要对SLP搜索区域设置上下界，也称为移动限制或步长边界，也就是 $\alpha <x-x^{a}<\beta$ 。如果步长边界太大，则 SLP 将在很长一段时间内围绕当前最优解振荡；如果步长边界太小，SLP 可能无法找到 NLP 的最优解。由于 SLP 算法的简单性，SLP 的大部分改进都在开发更好的启发式算法和新算法来调整步长边界。以下是一个简单的更新步长边界的算法：

计算：首先计算两个变量q和r，假设 $x^{a}$ 为旧解， $x^{a+1}$ 为新解，那么q代表两个解在NLP问题中的目标值减少量，r代表两个解在SLP问题中的目标值减少量

更新：基于q/r比值来更新步长边界的大小，如果 $q/r=1$ ，那么 SLP 问题完美地反映了 NLP 问题。如果 $q/r$ 接近1，比如 $0.75\leq q/r\leq 1.25$ ，增加步长边界。如果 $q/r$ 非常偏移1，比如 $q/r\leq 0.25,q/r\geq 1.25$ ，减少步长边界。如果为负值，表明对于NLP， $x^{a+1}$ 比 $x^{a}$ 更差，拒绝 $x^{a+1}$ ，减少步长边界，SLP用带更小步长边界的 $x^{a}$ 求解

2.3 完整的SLP算法

3.案例

3.1 example1

给定问题如下，用图表示，阴影部分为可行域，设置停止条件为前面提到的（3）和（4）

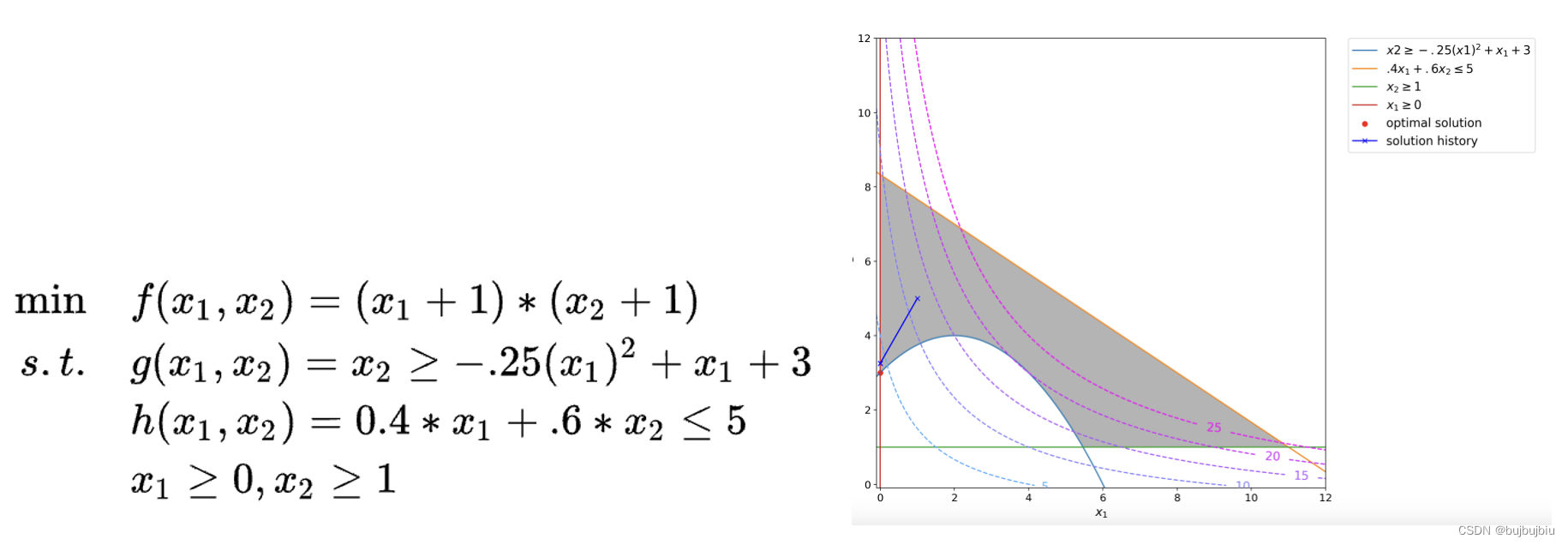
首先对非线性项计算梯度，将g(x1,x2)先写成标准形式，其梯度应该为[-0.5x1+1,-1]，资料上写的[-0.5x1,-1]，本人认为有误。但是由于案例只是说明过程，因此后面还是按照原本资料计算结果描述。h(x1,x2)为线性函数，不需要展开。使用前面介绍的Step Bounds方法更新边界，初始边界设为16，初始点为 $x_{1}=1,x_{2}=5$

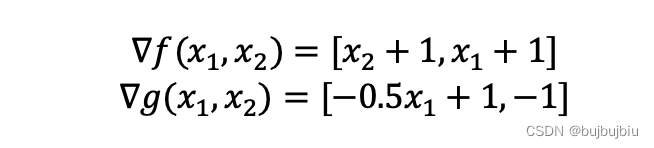
迭代第一次

首先计算在点(1,5)处的梯度，f函数为[6,2]，g函数为[-0.5,-1]，加入步长边界约束，得到如下在点(1,5)处的SLP模型

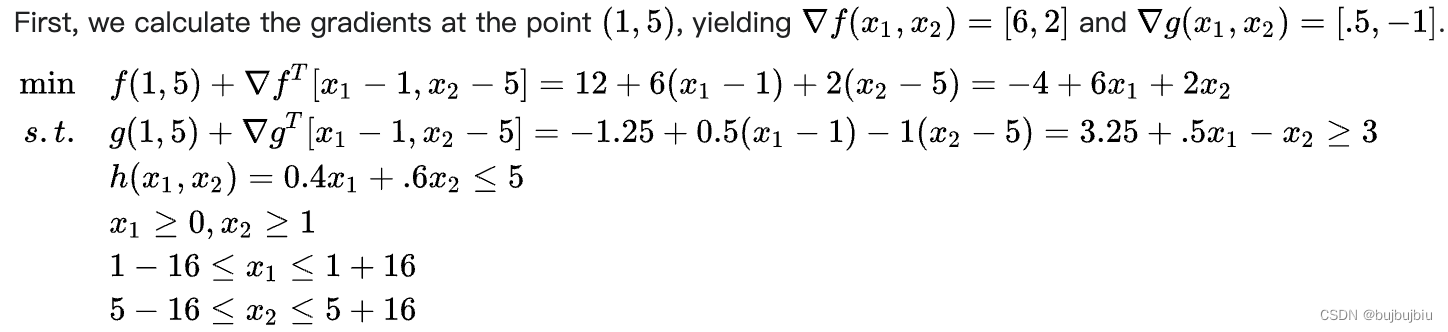
求解这个SLP模型，获得最优解： $f^{*}=2.5,x_{1}^{*}=0,x_{2}^{*}=3.25$ ，再计算q=4.25-12=-7.75，r=2.5-12=-9.5。所以q/r=0.815，接收这个点，步长边界增加至32。

迭代第二次

同上一次迭代过程，计算在点(0,3.25)处的梯度，f函数为[4.25,1]，g函数为[1,-1]，步长边界32

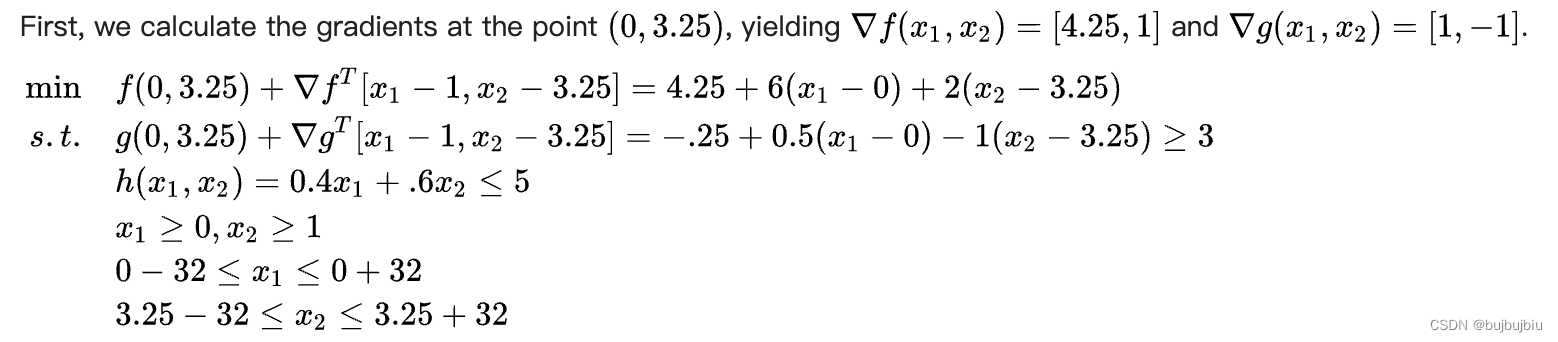
求解这个SLP模型，获得最优解： $f^{*}=4,x_{1}^{*}=0,x_{2}^{*}=3$ ，再计算q=-0.062，r=1.5，q/r=-0.041，拒绝这个点，步长边界减少至16。

迭代第三次

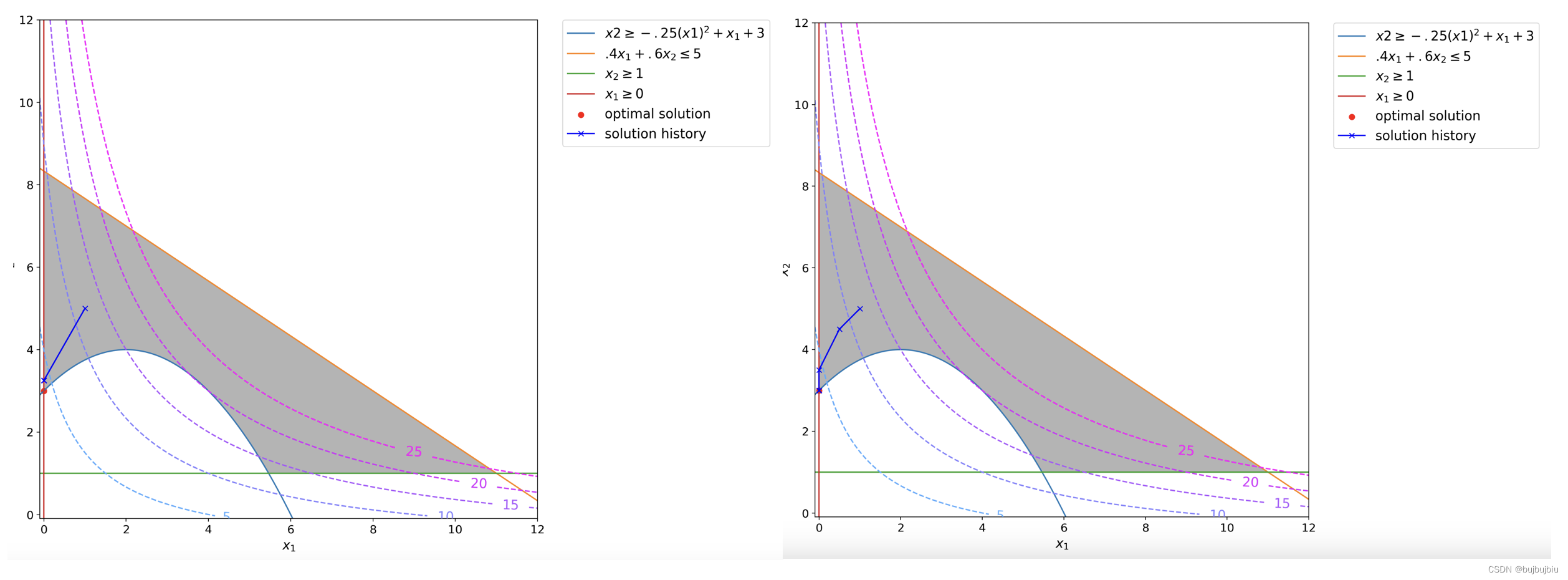
后续迭代会发现找到的新解会一直被拒绝，步长边界不断收缩。这是因为第一次选择的步长边界太大，问题会最终在20次迭代后终止。图上显示了步长分别为16和0.5的求解历史。

3.2 example2

在example1中，最优解是在定点，因此SLP会经过迭代后收敛，在example2中，最优解不在顶点处，给定下面问题，按照和example1一样的流程，计算梯度用一阶泰勒展开式代替，初始步长边界为16，初始点为(1,5)

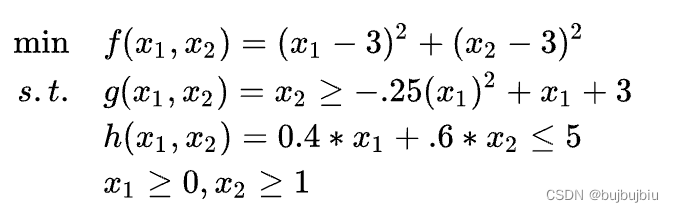
迭代第一次：SLP最优解-3.714，NLP为7.739，(4.375,5.428)，q/r=0.022，接收，步长边界减至8

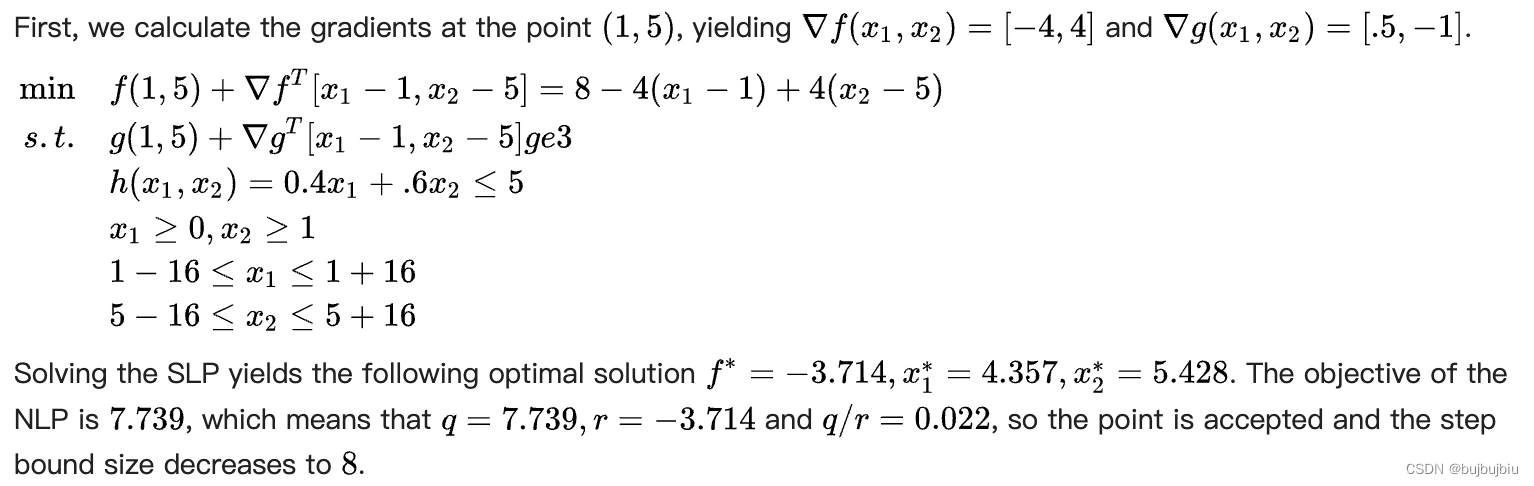
迭代第二次：SLP最优解-10.060，NLP为11.420，q/r=-0.579，拒绝，步长边界减至4

迭代第三次：SLP最优解-8.965，NLP为8.040，q/r=-0.057，拒绝，步长边界减至2

迭代第四次：SLP最优解-3.857，NLP为0.623，q/r=49.704，(3.663,3.428)，接受，步长边界减至1
迭代第五次：SLP最优解-0.093，NLP为1.412，q/r=0.209，（2.663，4.139），接受，步长边界减至0.5
迭代第六次：SLP最优解0.128，NLP为0.0551，（3.163，3.724），之后迭代不会出现比0.0551更优的解

在SLP中，步长边界和更新方式非常重要，会直接用影响结果，因此很多文献都致力于开发更有效的更新方式，比如启发式方法。

4.应用

混合可再生能源系统运营计划：2019年Vaccari和同事用SLP生成了短期运营计划，以满足电力和热负荷要求，最小化运营成本。每个设备都是一个NLP问题。
最优潮流问题Optimal Power Flow (OPF)：Mhanna 和 Mancarella 在 2021 年开发了一种 SLP 算法来解决最优潮流问题（非凸和非线性问题）
避障和轨迹规划：Plessen 及其同事在 2017 年通过使用基于空间的问题公式和 SLP 来连续改进规划轨迹，解决了自动驾驶车辆的轨迹规划和避障问题。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/627935.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！