一. 背景
那么我们为什么要用树状数组呢?
在解决一些区间求和的问题中 , 简单描述就是,对于一个给定的数组A,希望能够设计一个update函数来修改其中一个数的值,然后再设计一个sum函数来计算数组下标再给定参数l和r之间的值之和。关键点在于这两个函数可能被无数次调用,所以需要保证两个函数的复杂度都要小。
平时我们对这类问题常用的两种方法是 :
1>暴力算法
update
函数采用对数组直接修改的方式。
O(1) ,
对于sum
函数,返回数组 nums 中索引 left 和索引 right 之间( 包含 )的nums元素的和,但是这道题的操作数很大,会超时。
O(n)
2>前缀和算法
sum函数,考虑前缀和的方法,也就是采用动态规划的方法,设计一个新的数组sums来表示前缀和。
其基本思想为,
sums
[i]表示A[0]+A[1]+A[2]+...+A[i-1]。具体操作的时候我们只需要设置sums[i] = sums[i-1]+A[i-1]即可。
如果希望计算数组下标从l到r的区间和,只需要计算sums[r+1]-sums[l]即可。希望使用这种方式达到简化计算复杂度的目的。 但是,这时候需要考虑update函数,当我们对数组A直接进行修改值之后,我们发现sums数组也需要进行修改。
举个栗子:
原数组:A= {1,2,3,4,5}
前缀和数组:sums= {0,1,3,6,10,15}
分析:当我们对A[2]进行修改,将其原值3改为2的时候。

这样一来,对于update函数,我们的复杂度就会提高,可以认为是O(n),即使当前sum函数复杂度变为了O(1),这道题总的复杂度依然是O(n)。
所以说 , 遇到这类问题
首先需要能够快速计算区间和,其次要保证在修改了数组的值之后,对相关数据结构内容修改的操作数也要尽量少, 从而就引出了树状数组.
二.树状数组
树状数组是一个查询和修改复杂度都为log(n)的数据结构。主要用于数组快速单点修改和快速区间求和.
图解如下 :
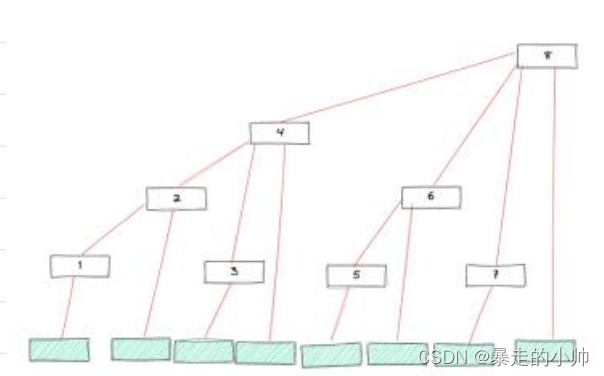
最底下一行绿色结点从左到右为原数组A,而带有数字的黑色结点就是树状数组C的结点 ,我们可以看到比如说C[8]结点,它的子结点有C[4],C[6],C[7],A[7](第八个绿色结点)而C[4],C[6],C[7]由分别有自己的子结点。 根据这张图,对于C[8]结点可以表示成:
C[8] = C[4] + C[6] +C[7] +A[7]
换一张图来理解一下:

这张图里表示的所有数字结点就是树状数组C,最下面一行从左到右同时也表示原数组A(包括空结点)。图中标出了修改原数组中第5个元素需要修改的所有结点值的更新过程和计算原数组中下标0~14的结点值之和的查询过程。
<1>
更新过程
根据上面树状数组的计算,我们参考这张图能够知道,C[5]是C[6]的子结点,C[6]是C[8]的子结点,而C[8]是C[16]的子结点,当我们修改A[4]的时候因为C[5] = A[4],所以C[5]会变化,导致C[6]变化,再导致C[8]变化,再导致C[16]变化,那么变化的值为多少呢,均为 A[4]新值减去A[4]旧值.
这里的思想和之前提到的前缀和有点相似,前缀和中是将sums[5]及后面所有的结点都要修改(因为这些结点都包含了A[4]结点的信息),但是这里只需要修改 C[5],C[6],C[8]和C[16]结点的信息(因为只有这几个结点包含了A[4]结点的信息),总体来说比起前缀和方法更新结点的时候对数据结构的更新就很快了.
那这是画图看出来要更新C[5[,C[6],C[8]和C[16]。那么具体是修改哪些结点呢?这里我们要从二进制的角度来看,重新画一张二进制的图,将所有结点上的十进制改为了二进制表示:

对应过来,我们会发现C[101]的值变化后,会影响C[110],进而影响C[1000]的值那么101和110和1000之间有什么关系呢?
可以归纳得出,110是由101加上1得到,1000是由110加上10得到,10000是由1000加上1000得到的
这里我们设计一个函数lowbit(int x)用于计算给定一个下标x,返回其二进制下标只保留最低位1会得到的那个数 , 也就是110为什么可以到101的一个算法 :
以x=5为例:
public int lowbit(int x){
return x & (-x);
}
正数的原码、反码、补码一样
示例: 5
原码: 0000 0101
反码:0000 0101
补码:0000 0101
负数的原码、反码、补码
(第一位表示符号位 1:负数 0:正数)
示例:
-5
原码: 1000 0101
反码:1111 1010(将原码除符号位外其它位按位取反)
补码:1111 1011 (反码+1)
那么-5也就是 1111 1011
7 & -7 = 0000 0001 = 2
所以我们在更改完tr[5] 之后下一个要更改的是 5+2 = 7,也就是tr[7]
那么在A[4](C[101])的值变了之后,我们只需要对101计算lowbit得到1,然后修改C[110]的值,然后计算110的lowbit得到10,再修改C[1000]的值,这样不断反复,直到当前需要修改的节点下标越界即可。这样我们就得到了我们的update函数:
//更新操作
public void update(int index,int val){
for (int i = index; i < this.tr.length; i += lowbit(index)) {
tr[i] += val;
}
}
整个复杂度为O(logn),因为每次lowbit导致移了一位,相当于反复对数组长度n除以2直到0.
<2>查询过程
查询过程是计算从A[0]到A[i]的所有值进行求和 , 如果我需要查询A[0]~A[14]之和,观察当前图我们会发现 8结点包含了0~7,12结点包含了8~11,14结点包含了12~13,15结点包含了14
那我们只需要将C[8],C[12],C[14],C[15]进行求和即可
同样的也是用到lowbit函数
//求和
public int sumRange(int index){
int sum = 0;
for (int i = index; i > 0; i-=lowbit(index)) {
sum += this.tr[i];
}
return sum;
}
查询过程相当于是求前缀和的过程,那么有了前缀和,我们就可以通过
前缀和作差得到其中部分区间和的答案
了。
这里使用到的复杂度为O(logn),因为每次lowbit移了一位,相当于反复对数组长度n除以2直到0的复杂度。