一、排序算法分类

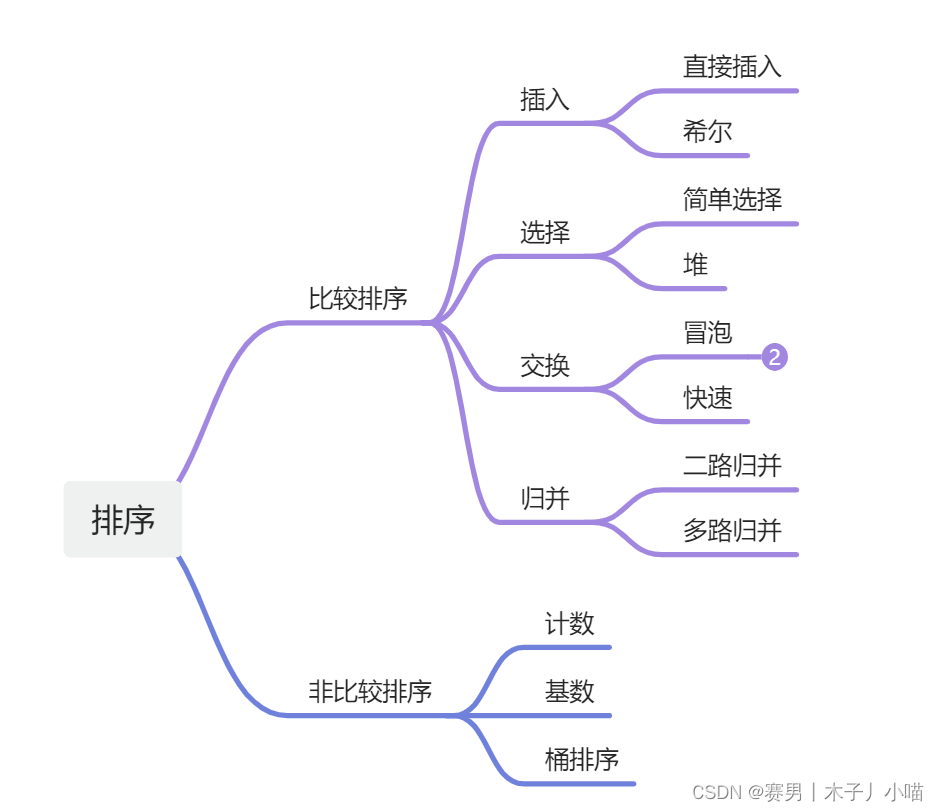
在这里插入图片描述

二、概念

算法的复杂性体现在运行该算法时的计算机所需资源的多少，计算机资源最重要的是时间和空间（即寄存器）资源，因此复杂度分为时间和空间复杂度。

2.1 时间复杂度

是一个定性描述该算法的运行时间的函数。
作用：指执行算法所需要的计算工作量。

2.2 空间复杂度

是对一个算法在运行过程中临时占用存储空间大小的量度，记做S(n)=O(f(n))。
比如直接插入排序的时间复杂度是O(n²),空间复杂度是O(1) 。而一般的递归算法就要有O(n)的空间复杂度了，因为每次递归都要存储返回信息。

2.3 稳定性

假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。

三、表格比较

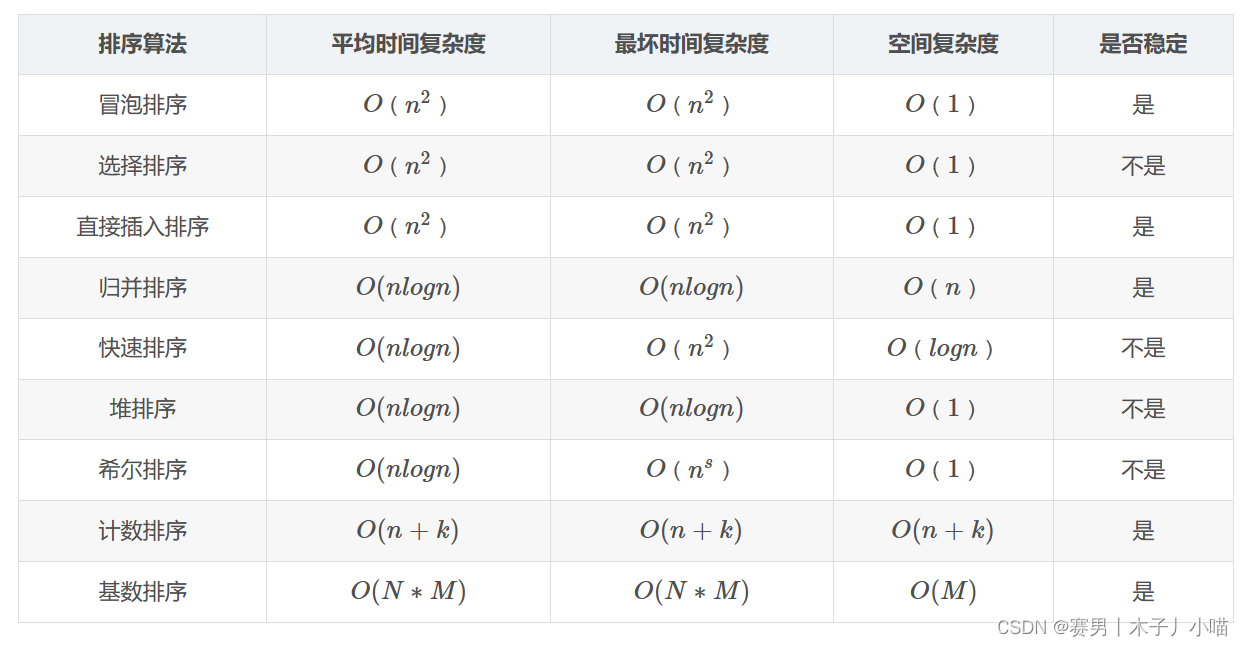
在这里插入图片描述

注意

1：希尔排序的平均时间复杂度，还有一种表示为O(n^1.3)
2：基数排序时间复杂度O（N*M），其中N为数据个数，M为数据位数。
3：归并排序可以通过手摇算法将空间复杂度降到O（1），但是时间复杂度会提高。
4：关于logⁿ的底数看下面的解释
5：分治法和树形，时间复杂度是nlogn
在这里插入图片描述

四、部分排序分析

正序选择插入和冒泡，只比较，不交换反之，倒序时尽量不选择插入和冒泡
有序时尽量不选择快排，因为使用不到分治。

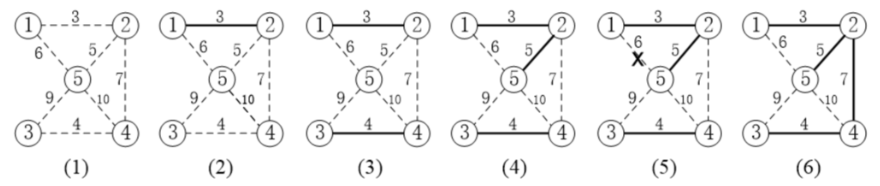
4.1 直接插入排序

图示

在这里插入图片描述

代码

public class InsertSort {
    //核心代码---开始
    public static void sort(Comparable[] arr){

        int n = arr.length;
        for (int i = 0; i < n; i++) {
            // 寻找元素 arr[i] 合适的插入位置
            for( int j = i ; j > 0 ; j -- )
                if( arr[j].compareTo( arr[j-1] ) < 0 )
                    swap( arr, j , j-1 );
                else
                    break;
        }
    }
    //核心代码---结束
    private static void swap(Object[] arr, int i, int j) {
        Object t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;
    }

    public static void main(String[] args) {

        Integer[] arr = {1,9,6,5,7,6,8,2,4};
        sort(arr);
        for( int i = 0 ; i < arr.length ; i ++ ){
            System.out.print(arr[i]);
            System.out.print(' ');
        }
    }
}

4.2 冒泡排序

图示

在这里插入图片描述

代码

//冒泡排序
void BubbleSort(int* arr, int n)
{
	int end = n;
	while (end)
	{
		int flag = 0;
		for (int i = 1; i < end; ++i)
		{
			if (arr[i - 1] > arr[i])
			{
				int tem = arr[i];
				arr[i] = arr[i - 1];
				arr[i - 1] = tem;
				flag = 1;
			}
		}
		if (flag == 0)
		{
			break;
		}
		--end;
	}
}

4.3 快速排序

图示

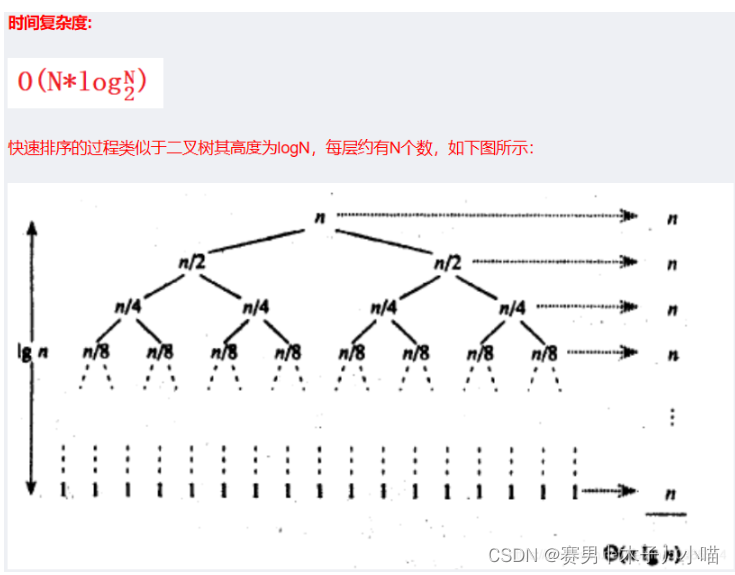
在这里插入图片描述

代码

void Quick_Sort(int *arr, int begin, int end){
    if(begin > end)
        return;
    int tmp = arr[begin];
    int i = begin;
    int j = end;
    while(i != j){
        while(arr[j] >= tmp && j > i)
            j--;
        while(arr[i] <= tmp && j > i)
            i++;
        if(j > i){
            int t = arr[i];
            arr[i] = arr[j];
            arr[j] = t;
        }
    }
    arr[begin] = arr[i];
    arr[i] = tmp;
    Quick_Sort(arr, begin, i-1);
    Quick_Sort(arr, i+1, end);
}

五、结构化记忆（小窍门）

5.1 结构化

是
指将逐渐积累起来的知识加以归纳和整理，使之条理化、纲领化，做到纲举目张。知识是逐渐积累的，但在头脑中不应该是堆积的。知识是有组织、有系统的，知识点按层次排列，而且知识点之间有内在联系，具有结构层次性。

5.2 我的结构化

我们都知道数据结构，数据结构指相互之间存在一种或多种特定关系的数据元素的集合，我们也可以把身边一切东西放在一起，去创造它们之间的关系。
现在就给大家分享一下我对七种比较排序的时间复杂度、空间复杂度和稳定性进行的“胡乱”结构化，请结合上面的二维表：
先来看时间复杂度（平均时间复杂度、最好时间复杂度、最坏时间复杂度）：
1、找共性：
首先看到有些排序这三个复杂度一样，分别是直接选择排序，堆排序和归并排序，其中直接选择排序、堆排序属于选择排序，我提取了它们的首字母（归并、选择=GX）,GX让我想到了共享，这不是刚好符合它们的特征吗，共享同一个时间复杂度。他们三个的区别是，直接选择排序是O(n²)，归并和堆排序是nlogn。
2、找联系：
我们顺着nlogn继续往下找，快速排序也是nlogn，但是它不属于第一分类的“共享”，说明三者不一样，那哪个不一样呢，是最坏时间复杂度为n²。（n²>nlogn）
3、排除：
七个排序还剩下三个（冒泡、直接插入和希尔排序），这三个又有什么特点呢？
冒泡、直接插入和希尔排序他们在数组基本有序的情况下，只需要执行n次逻辑代码，最好时间复杂度都是O（n),冒泡、直接插入最坏和平均都是n²。剩下一个希尔，因为有步长，所以比较特殊，单独理解就好。
总结一下整个过程就是：
gx–nlogn–(7-4)–2+1
在这里插入图片描述
再说空间复杂度：找到的共性是大部分都是O(1)，只有两个比较特殊，一个是归并，一个是快排，（这个结构化的过程交给你来了，试试吧小伙伴，你会发现很有意思）；
稳定性：快选希堆不稳定，其余稳定。