目录
一、前言
二、相关概念
1、最小生成树
2、Prim算法(对结点进行操作)
3、kruskal 算法(对边进行操作)
三、例题
1、修建公路(lanqiaoOJ题号1124)
1、Prim算法题解
2、Kruskal算法
一、前言
很久没更新了蓝桥杯算法栏目了,明天国赛了,浅更新一下,求最小生成树,相信大家都会,本文带大家来回顾一下这两个非常简单好用的算法。(贵在理解算法逻辑,代码什么的都是次要)
二、相关概念
1、最小生成树
- 在无向图中,连通而且不含有圈(环路)的图,称为树。
- 最小生成树MST:一个有n个结点的连通图的生成树是原图的极小连通子图,包含原图中的所有n个结点,并旦边的权值之和最小。
- 两种算法:prim、kruskal
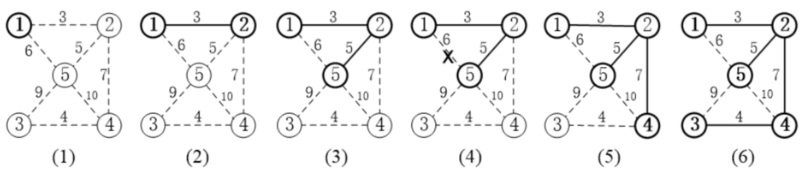
2、Prim算法(对结点进行操作)
- 对点进行贪心操作:“最近的邻居一定在 MST 上”。
- 从任意一个点 u 开始,把距离它最近的点 v 加入到 MST 中;下一步,把距离 {u, v} 最近的点 w 加入到 MST 中;继续这个过程,直到所有点都在 MST 中。
补充:1956年,Dijkstra在一篇论文中同时提出了这两个算法,两个算法的思想基本一样,都是基于贪心法来扩展结点,执行步骤十分相似,代码只有微小差别。
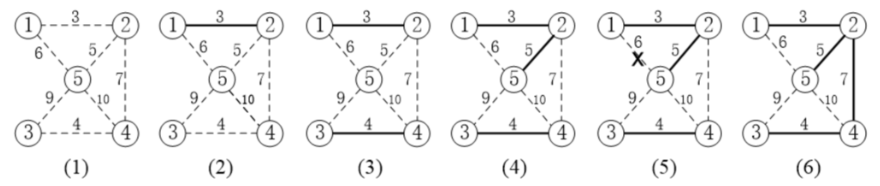
3、kruskal 算法(对边进行操作)
- 对边进行贪心操作:“最短的边一定在 MST 上”。
- 从最短的边开始,把它加入到 MST 中;在剩下的边中找最短的边,加入到 MST 中;继续这个过程,直到所有点都在 MST 中。
补充:
kruskal 算法的 2 个关键技术:
1)对边进行排序。
2)判断圈,即处理连通性问题。这个问题用并查集简单而高效,并查集是 kruskal 算法的实现基础。
三、例题
1、修建公路(lanqiaoOJ题号1124)
链接:用户登录
可能部分同学没办法进入到链接刷这道题,我把题目放上来。
题目描述
L 城一共有 N 个小区。
小明是城市建设的规划者,他计划在城市修 M 条路,每修建一条路都要支付工人们相应的工钱(需要支付的工钱 == 路的长度)。
然而小明所拿到的经费并不够支付修建 M 条路的工钱,于是迫于无奈,他只能将计划改变为修建若干条路,使得 N 个小区之间两两联通。
小明希望尽量剩下更多的经费投入到别的项目中,因此请你通过程序帮他计算出完成计划所需的最低开销。
输入描述
输入第一行包含三个正整数 N,M。
第 2 到 M+1 行每行包含三个正整数 u, v, w,表示 u↔v 之间存在一条距离为 w 的路。
1≤N≤10^5,0≤m≤3×10^5,1≤ui,vi≤N,0≤wi≤10^9。
输出描述
输出占一行,包含一个整数,表示完成计划所需的最低开销。
若无法完成计划,则输出 −1。
输入输出样例
输入:
5 6 1 2 2 1 3 7 1 4 6 2 3 1 3 4 3 3 5 2输出:
8运行限制
- 最大运行时间:3s
- 最大运行内存:256M
1、Prim算法题解
python代码(AC):
import sys
from heapq import *
input=sys.stdin.readline
def prim():
ans,cnt=0,0
q=[]
vis=[False for _ in range(n+1)]
heappush(q,(0,1))
while q and cnt<n:
w,u=heappop(q) #pop出距离集合最近的点u
if not vis[u]:
vis[u]=True
ans+=w
cnt+=1
for v,w in e[u]:
heappush(q,(w,v))
if cnt!=n:
print(-1)
else:
print(ans)
n,m=map(int,input().split())
e=[[] for _ in range(n+1)]
for i in range(m):
u,v,w=map(int,input().split())
e[u].append((v,w))
e[v].append((u,w))
prim()2、Kruskal算法
python代码(AC):
import sys
input=sys.stdin.readline
def init():
for i in range(n+1):
s.append(i)
def find(x):
if s[x]==x:
return x
s[x]=find(s[x])
return s[x]
def kruskal():
cnt=0
ans=0
e.sort(key=lambda tup:tup[2])
init()
for i in range(m):
x,y=e[i][0],e[i][1]
e1,e2=find(x),find(y)
if e1==e2:
continue
ans+=e[i][2]
s[find(y)]=find(x)
cnt+=1
if cnt==n-1:
break
if cnt!=n-1:
print(-1)
else:
print(ans)
e=[]
s=[]
n,m=map(int,input().split()) #顶点数,边数
for i in range(m):
u,v,w=map(int,input().split())
e.append((u,v,w))
kruskal()根据这一题相信大家都能很好的理解Prim和Kruskal算法。
以上,求最小生成树(Kruskal算法和Prim算法)
煮好!