数字图像处理实验报告

news2024/11/26 15:24:50

目录

实验二、图像在空间域上的处理方法

实验三、图像在频率域上的处理方法

实验二、图像在空间域上的处理方法

一、实验目的

  1. 了解图像亮（灰）度变换与空间滤波的意义和手段；
  2. 熟悉图像亮（灰）度变换与空间滤波的MATLAB函数和语法；
  3. 熟练掌握应用MATLAB软件编程进行图像亮（灰）度变换与空间滤波的方法；
  4. 完成数字图像的对比度增强和直方图均衡化，设计空间域平滑和锐化滤波器，掌握数字图像在空间域的基本处理方法。

二、实验环境

MATLAB 2014以上版本、Win 8\10\11 系统

三、实验原理

图像亮（灰）度变换与空间滤波属于在空间域内处理图像，是直接对图像的像素进行处理。有两种重要的空间域处理方法，即亮度（或灰度级）变换与空间滤波，后一种方法有时称为邻域处理或空间卷积。

图像亮（灰）度变换采用MATLAB工具箱中的亮度变换函数、直方图处理函数等函数及其相应的语法格式对实验一生成的图像进行处理；空间滤波采用MATLAB工具箱中的标准（线性和非线性）空间滤波器对图像进行空间滤波处理。

涉及函数：imread、size、figure、imshow、subplot、imadd、imsubtract 、rgb2gray、imhist、histeq、imnoise、medfilt2

四、实验内容

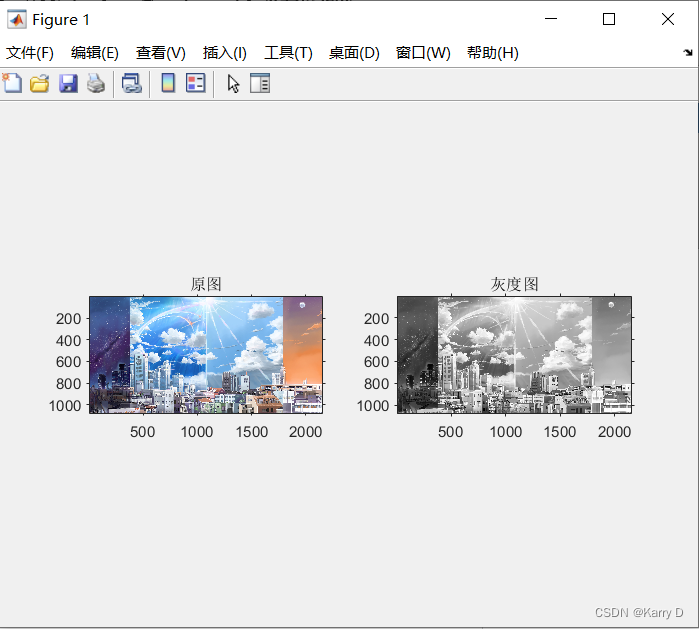
（1）新建一个m文件，从桌面示例图像文件夹中读取一张彩色图像，转换为灰度图，读取该图像尺寸，并在一个figure窗口同时展示，标题分别为（“原图”）及（“灰度图”）。

代码：

clc;clear;clear all;

RGB=imread('V.jpg'); %图像读入

I=rgb2gray(RGB);   %把 RGB 图像转换成灰度图像

subplot(121);imshow(RGB),axis on,title("原图");

subplot(122);imshow(I),axis on,title("灰度图");

输出结果截图：

（2）读取一张彩色图像，转换为灰度图，使用imadd及imsubtract 分别对图像进行亮度增和减操作，数值为自己学号末位数×2，并在一个figure窗口同时展示，标题分别为“原图”、“灰度图”、“提亮结果”、“亮度降低结果”。点击右侧工作区中对应图像矩阵，观察亮度增减前后数值变化。

代码：

clc;clear;clear all;

RGB=imread('V.jpg'); %图像读入

I=rgb2gray(RGB);   %把 RGB 图像转换成灰度图像

RGB2=imadd(RGB,20);

RGB3=imsubtract(RGB,20); %学号尾数为10

subplot(221);imshow(RGB),axis on,title("原图");

subplot(222);imshow(I),axis on,title("灰度图");

subplot(223);imshow(RGB2),axis on,title("提亮结果");

subplot(224);imshow(RGB3),axis on,title("亮度降低结果");

输出结果截图：

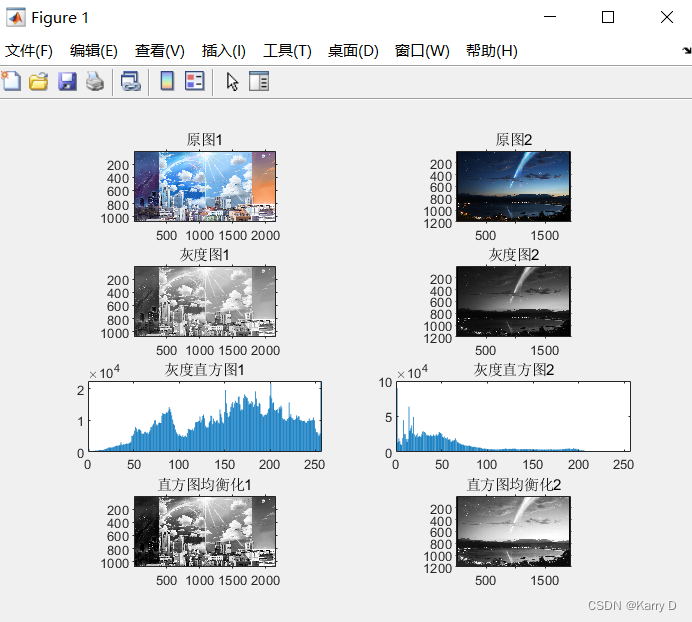
（3）读取两张彩色图像并转换为灰度图，使用imhist函数显示该图像的直方图，并使用histeq函数分别进行进行直方图均衡化处理。同一个figure窗口中输出，标题分别为“原图1”、“灰度图1”，“原图2”，“灰度图2”、“灰度直方图1”、“灰度直方图2”、“直方图均衡化1”、“直方图均衡化2”。

观察不同图像对应灰度直方图的特征有何差异，对比同一张图直方图均衡化前后的灰度分布差异。

代码：

clc;clear;clear all;

RGB=imread('V.jpg'); %图像读入

RGB1=imread('V1.jpg'); %图像读入

I=rgb2gray(RGB);   %把 RGB 图像转换成灰度图像

I1=rgb2gray(RGB1);   %把 RGB 图像转换成灰度图像

subplot(421);imshow(RGB),axis on,title("原图1");

subplot(422);imshow(I),axis on,title("灰度图1");

subplot(423);imshow(RGB1),axis on,title("原图2");

subplot(424);imshow(I1),axis on,title("灰度图2");

% 计算直方图

hist = imhist(I);

hist1 = imhist(I1);

% 对图像进行直方图均衡化处理

img_eq = histeq(I);

img_eq1 = histeq(I1);

subplot(425);bar(hist);axis on,title("灰度直方图1");

subplot(426);bar(hist1);axis on,title("灰度直方图2");

subplot(427);histeq(I),axis on,title("直方图均衡化1");

subplot(428);histeq(I1),axis on,title("直方图均衡化2");

输出结果截图：

（4）读取一张彩色图像并转换为灰度图，使用imnoise添加椒盐噪声，例如I1=imnoise(I,’salt& pepper’,0.04); 分别使用3*3、5*5、7*7、9*9大小的模板进行中值滤波，在相同figure中输出，标题分别为“原图”、“添加椒盐噪声”、“x*x模板中值滤波”。

代码：

% 读取彩色图像并转换为灰度图

clc;clear;clear all;

RGB=imread('V.jpg'); %图像读入

I=rgb2gray(RGB);   %把 RGB 图像转换成灰度图像

% 添加椒盐噪声

I_noise = imnoise(I, 'salt & pepper', 0.04);

% 使用不同大小的模板进行中值滤波

I_median3 = medfilt2(I_noise, [3 3]);

I_median5 = medfilt2(I_noise, [5 5]);

I_median7 = medfilt2(I_noise, [7 7]);

I_median9 = medfilt2(I_noise, [9 9]);

subplot(321);imshow(RGB),axis on,title("原图");

subplot(322);imshow(I_noise),axis on,title("添加椒盐噪声");

subplot(323);imshow(I_median3),axis on,title("3*3模板中值滤波");

subplot(324);imshow(I_median5),axis on,title("5*5模板中值滤波");

subplot(325);imshow(I_median7),axis on,title("7*7模板中值滤波");

subplot(326);imshow(I_median9),axis on,title("9*9模板中值滤波");

输出结果截图：

（5）读取一张彩色图像并转换为灰度图，利用im2bw函数转换为“二值图像”，分别使用sobel算子及Laplacian算子进行锐化，在相同figure中输出，标题分别为“原图”、“二值图像”、“sobel算子锐化”、“拉普拉斯算子锐化”。

提示：H=fspecail (‘soble’); J=filter2(H,I1)；

代码：

% 读取一张彩色图像并转换为灰度图

clc;clear;clear all;

img = imread('V.jpg');

gray_img = rgb2gray(img);

% 利用im2bw函数转换为“二值图像”

bw_img = im2bw(gray_img);

% 使用sobel算子进行锐化

sobel_img = edge(bw_img, 'sobel');

% 使用Laplacian算子进行锐化

laplace_img = edge(bw_img, 'log');

% 在相同figure中输出结果

figure;

subplot(2,2,1);

imshow(img);

title('原图');

subplot(2,2,2);

imshow(gray_img);

title('灰度图');

subplot(2,2,3);

imshow(sobel_img);

title('Sobel算子锐化');

subplot(2,2,4);

imshow(laplace_img);

title('Laplacian算子锐化');

输出结果截图：

实验三、图像在频率域上的处理方法

一、实验目的

  1. 了解图像频域处理的意义和手段；
  2. 熟悉离散傅里叶变换的基本性质；
  3. 熟练掌握图像傅里叶变换的方法及应用；
  4. 通过实验了解二维频谱的分布特点；
  5. 通过本实验掌握利用MATLAB的工具箱实现数字图像的频域处理，构建各式常见频率域滤波器，并熟悉其特点与应用场景。

二、实验环境

MATLAB 2014以上版本、Win 8\10\11 系统

三、实验原理

图像的频率是图像在平面空间上的梯度，是表征图像中图像变化剧烈程度的指标。例如，大面积的海洋在图像中是一片图像变化缓慢的区域，对应的频率值很低;而地表属性变换剧烈的边缘区域在图像中则是一片图像变化剧烈的区域，对应的频率值较高。频域滤波增强是利用图像变换方法将原来的图像空间中的图像以某种形式转换到其他空间中，然后利用该空间的特有性质方便地处理图像，最后再转换回原来的图像空间中，从而得到处理后的图像。图像的频率域处理图像处理中占有重要的地位，在图像的去噪、图像压缩、特征提取和图像识别方面发挥着重要的作用。

图像频率域采用MATLAB工具箱中的傅里叶变换函数、滤波函数等函数及其相应的语法格式图像进行处理；

在MATLAB 中，函数fft、fft2和fftn分别可以实现一维、二维和N维DFT 算法:而函数 ifft、ifft2 和 ifftn 则用来计算反 DFT。fftshift 函数可以把傅里叶操作(fft，fft2，fftn)得到的结果中的零频率成分移到矩阵的中心，这样有利于观察频谱；

涉及函数：imread、figure、imshow、subplot、rgb2gray、log、abs、fft、fft2、fftshift、ifft2

四、实验内容

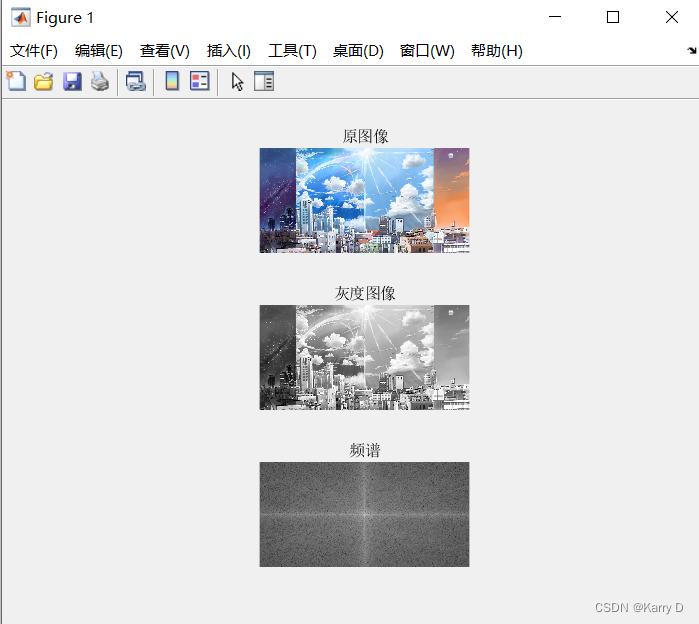
（1）新建一个m文件，从桌面示例图像文件夹中读取一张彩色图像，转换为灰度图，利用傅里叶变换函数fft2与fftshift显示图像的傅里叶变换频谱图，并在一个figure窗口同时展示，标题分别为“原图”、“灰度图”、“变换频谱”。

代码：

clc;clear;clear all;

I=imread('V.jpg');

figure

subplot(311),imshow(I),title("原图像")

GrayI=rgb2gray(I);

subplot(312),imshow(GrayI),title('灰度图像')

fft2(GrayI);

S=fftshift(fft2(GrayI));

subplot(313),imshow(log(abs(S)),[]),title('频谱')

输出结果截图：

（2）读取一张彩色图像，转换为灰度图，使用fft2进行傅里叶变换，接着使用ifft2进行傅里叶逆变换，并在一个figure窗口同时展示，标题分别为“原图”、“灰度图”、“二维傅里叶变换”、“傅里叶逆变换”。观察变换前后图像，及对应图像矩阵是否与原图相同。

代码：

clc;clear;clear all;

% 读取彩色图像

rgb_img = imread('V.jpg');

% 转换为灰度图

gray_img = rgb2gray(rgb_img);

% 进行二维傅里叶变换

fft_img = fft2(gray_img);

% 进行傅里叶逆变换

ifft_img = ifft2(fft_img);

% 显示图像

figure;

subplot(2, 2, 1);

imshow(rgb_img);

title('原图');

subplot(2, 2, 2);

imshow(gray_img);

title('灰度图');

subplot(2, 2, 3);

imshow(abs(fftshift(fft_img)), []);

title('二维傅里叶变换');

subplot(2, 2, 4);

imshow(abs(ifft_img), []);

title('傅里叶逆变换');

输出结果截图：

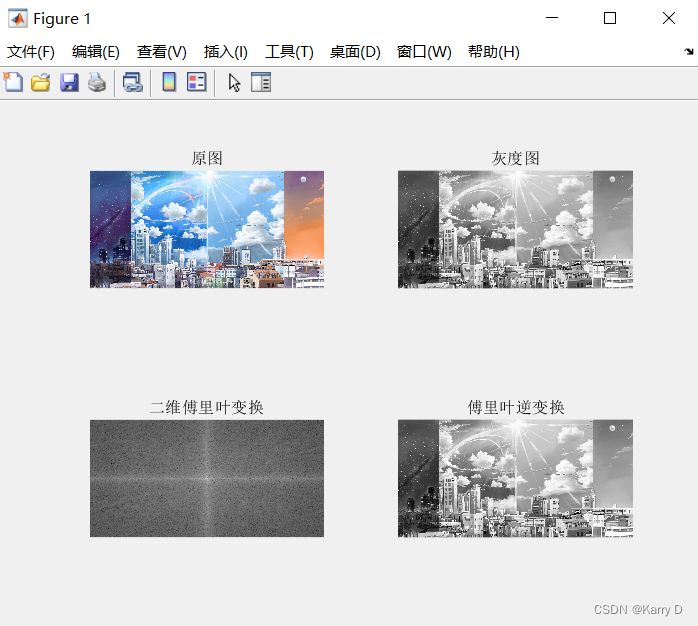
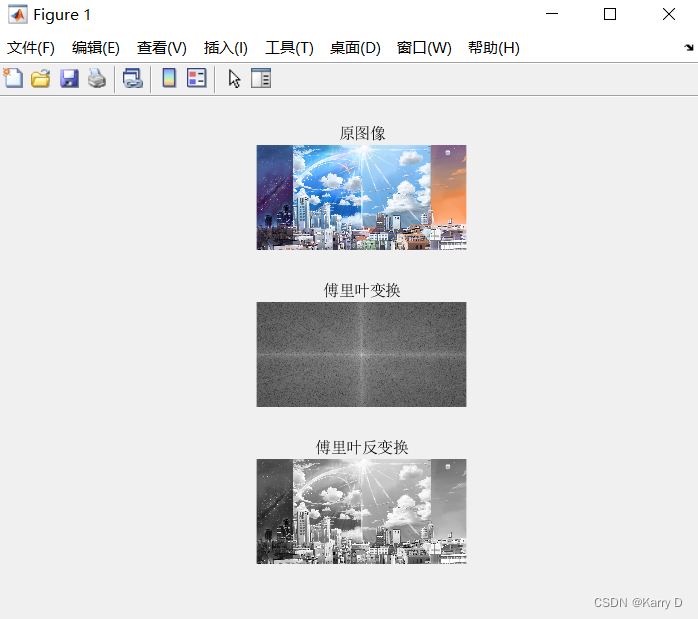
（3）读取一张彩色图像并转换为灰度图，接着对图像进行傅里叶正反变换，对比变换前后是否相同。同一个figure窗口中输出，标题分别为“原图”、“傅里叶变换”，“傅里叶反变换”。

代码：

clc;clear;clear all;

I=imread('V.jpg');

figure

subplot(311),imshow(I),title("原图像")

A=rgb2gray(I);

B=fft2(A);

C=fftshift(B);

subplot(312),imshow(log(abs(C)),[]),title('傅里叶变换')

D=ifft2(B);

subplot(313),imshow(uint8(abs(D))),title('傅里叶反变换')

输出结果截图：

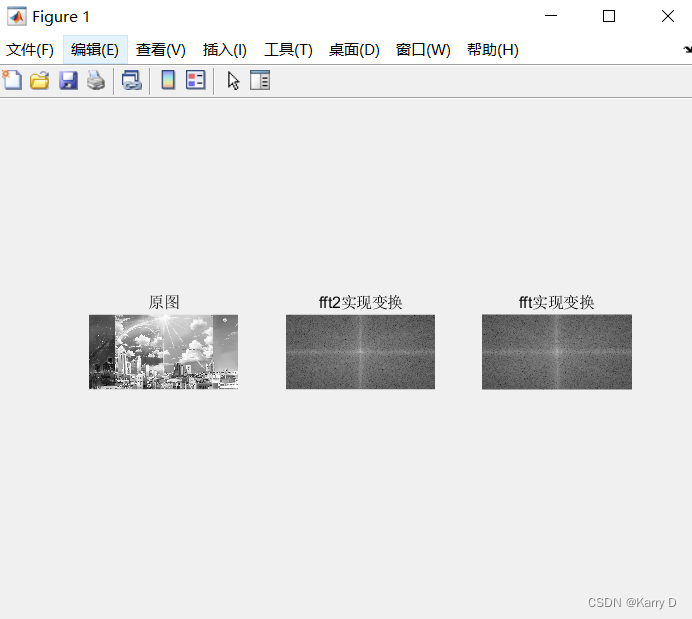
（4）读取一张彩色图像并转换为灰度图，使用fft函数及fft2函数验证二维离散傅里叶变换可分解为两个一维离散傅里叶变换（先行变换，后列变换）在相同figure中输出，标题分别为“原图”、“fft2实现变换”、“fft实现变换”。

代码：

clc;clear;clear all;

% 读取彩色图像并转换为灰度图

img = imread('V.jpg');

gray_img = rgb2gray(img);

% 在同一figure中输出原图

subplot(1,3,1);

imshow(gray_img);

title('原图');

% 使用fft2函数进行二维离散傅里叶变换

fft2_img = fft2(gray_img);

% 在同一figure中输出使用fft2函数实现的变换结果

subplot(1,3,2);

imshow(log(abs(fftshift(fft2_img))),[]);

title('fft2实现变换');

% 使用fft函数进行一维离散傅里叶变换（先行变换）

fft_row_img = fft(gray_img,[],1);

% 使用fft函数进行一维离散傅里叶变换（后列变换）

fft_col_img = fft(fft_row_img,[],2);

% 在同一figure中输出使用fft函数实现的变换结果

subplot(1,3,3);

imshow(log(abs(fftshift(fft_col_img))),[]);

title('fft实现变换');

输出结果截图：

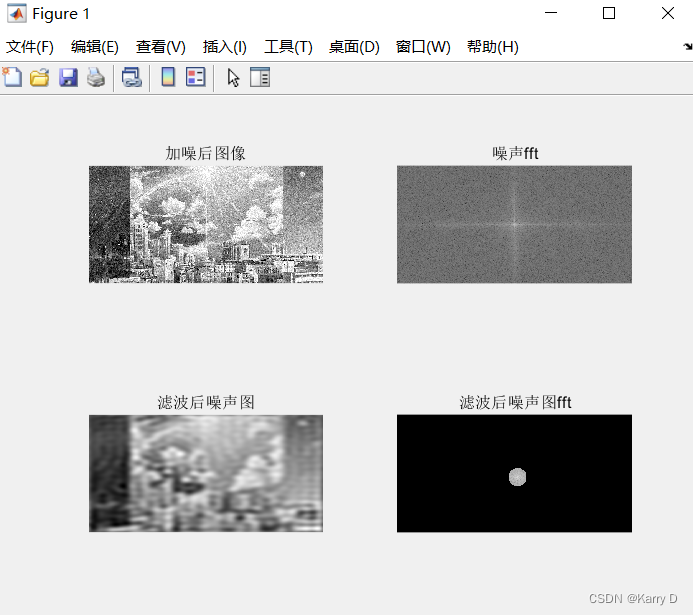
（5）读取一张彩色图像并转换为灰度图，使用imnoise函数加入高斯白噪声，绘制加噪后图像，使用fft函数绘制加噪后图像傅里叶频谱图。接着设计一个截止频率D0=M*10（其中M=学号末位数）的理想低通滤波器(ILPF)对图像进行滤波处理，绘制滤波后噪声图及滤波后的傅里叶频谱图。上述结果在同一figure中显示，标题分别为“加噪后图像”、“噪声fft”、“滤波后噪声图”、“滤波后噪声图fft”。

提示：

①对于大小为M*N的图像，频率点(u, v)与频率中心的距离为D(u, v)，其表达式为：

②理想低通滤波器的产生公式为：

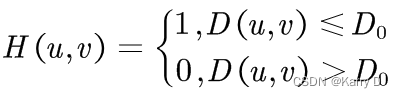
代码：

clc;clear;clear all;

% 读取彩色图像并转换为灰度图

rgb_img = imread('V.jpg');

gray_img = rgb2gray(rgb_img);

% 加入高斯白噪声

noisy_img = imnoise(gray_img, 'gaussian');

% 绘制加噪后图像

figure;

subplot(2,2,1);

imshow(noisy_img);

title('加噪后图像');

% 使用FFT函数绘制加噪后图像傅里叶频谱图

noisy_fft = fft2(noisy_img);

noisy_fft_shifted = fftshift(noisy_fft);

noisy_fft_mag = abs(noisy_fft_shifted);

subplot(2,2,2);

imshow(log(1+noisy_fft_mag), []);

title('噪声fft');

% 设计理想低通滤波器(ILPF)对图像进行滤波处理

M = 2; % 学号末位数是0(更换为2)

D0 = M*10;

[height, width] = size(noisy_img);

[x, y] = meshgrid(1:width, 1:height);

center_x = floor(width/2)+1;

center_y = floor(height/2)+1;

d = sqrt((x-center_x).^2 + (y-center_y).^2); % 欧几里得距离

H_ILPF = double(d<=D0); % 理想低通滤波器

% 对图像进行滤波处理

noisy_fft_filtered_shifted = noisy_fft_shifted .* H_ILPF;

noisy_filtered = real(ifft2(ifftshift(noisy_fft_filtered_shifted)));

% 绘制滤波后噪声图及滤波后的傅里叶频谱图

subplot(2,2,3);

imshow(noisy_filtered, []);

title('滤波后噪声图');

filtered_fft = fft2(noisy_filtered);

filtered_fft_shifted = fftshift(filtered_fft);

filtered_fft_mag = abs(filtered_fft_shifted);

subplot(2,2,4);

imshow(log(1+filtered_fft_mag), []);

title('滤波后噪声图fft');

输出结果截图：

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/627400.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

买法拍房需要注意什么

买法拍房需要注意什么

法拍房&#xff0c;由于其价格亲民、房屋信息透明度高、竞拍过程公平公正而受到越来越多的人开始关注。但是其中又有着许多的风险及相关的注意事项。那么&#xff0c;如何做到成功“捡漏”&#xff0c;买法拍房需要注意什么呢? 买法拍房需要注意什么 1、隐藏的各种收费 税费&a…
阅读更多...
优思学院｜质量和可靠性是同一件事吗？

优思学院｜质量和可靠性是同一件事吗？

什么是质量&#xff1f; 质量是什么&#xff1f;早期的定义是“整体上用来决定产品或服务能否满足使用目的之固有性质与性能总合”&#xff0c;换言之&#xff0c;质量就是“可显示出品质与服务好坏的东西”。 不过&#xff0c;关于质量的想法随时代变化&#xff0c;有范围愈…
阅读更多...
专访：诺奖得主Alain Aspect谈量子的挑战与未来

专访：诺奖得主Alain Aspect谈量子的挑战与未来

光子盒研究院出品 近期&#xff0c;诺贝尔物理学奖获得者Alain Aspect在接受电子工程专辑(EE Times Europe)采访时说&#xff1a;“诺贝尔奖是由于显示了纠缠的非凡特性而获得的&#xff0c;但我还研究了许多其他惊人的量子现象&#xff0c;包括将原子冷却到一光子反冲力以下。…
阅读更多...
JavaWebHtmlCSS总结

JavaWebHtmlCSS总结

目录 JavaWeb概述1.访问web的原理2.C/S软件和B/S软件区别3.静态网站和动态网站 HTMLHTML的概述Table表格详细用法见W3CSchool.chm合并单元格课程表 img标签table和img标签组合使用a标签表单表单Get提交和post提交 div和span CSS1.CSS概述2.CSS语法3.CSS三种写法行内样式内部样式…
阅读更多...
专访泛境科技：如何借助3DCAT实时云渲染打造元宇宙解决方案

专访泛境科技：如何借助3DCAT实时云渲染打造元宇宙解决方案

随着5G、VR/AR等技术的发展&#xff0c;元宇宙&#xff08;Metaverse&#xff09;这一概念越来越受到关注。元宇宙是一个由虚拟世界构成的网络空间&#xff0c;其中人们可以通过数字化的身份和形象进行各种社交、娱乐、创作和商业活动。元宇宙的核心是虚拟场景&#xff0c;它是…
阅读更多...
教育信息化时代，如何打造中学理科信息化实验操作考场方案

教育信息化时代，如何打造中学理科信息化实验操作考场方案

近年来&#xff0c;我国考试招生制度不断改进完善&#xff0c;初步形成了相对完整的考试招生体系。但随着教育事业的逐步发展&#xff0c;国务院明确提出了改革考试形式和内容&#xff1a;完善中学学业水平考试&#xff0c;规范中考学生综合素质评价&#xff0c;加快推进中学院…
阅读更多...
Promise.allSettled优化并行接口报错

Promise.allSettled优化并行接口报错

问题背景 后端需要前端请求同一个接口三次&#xff0c;每次传参不同可以获取到不同的结果>构成计算资源的选项。 其中一个接口传参获取数据报错&#xff0c;导致整个计算资源都没有可选择的options&#xff1a; 前端代码使用Promise.all获取res1, res2, res3返回结果&…
阅读更多...
云原生docker-cgroup资源限制

云原生docker-cgroup资源限制

概述 Docker 通过 Cgroup 来控制容器使用的资源配额&#xff0c;包括 CPU、内存、磁盘三大方面&#xff0c; 基本覆盖了常见的资源配额和使用量控制。 Cgroup 是 ControlGroups 的缩写&#xff0c;是 Linux 内核提供的一种可以限制、记录、隔离进程组所使用的物理资源(如 CPU、…
阅读更多...
【剑指offer】调整数组顺序使奇数位于偶数前面

【剑指offer】调整数组顺序使奇数位于偶数前面

文章目录 题目思路相对位置可以改变的思路相对位置不能改变的思路 题目 题目链接入口&#xff1a;调整数组顺序使奇数位于偶数前面 示例1&#xff1a; 输入&#xff1a;[1,2,3,4,5,6] 结果&#xff1a;[1,3,5,2,4,6] 示例2&#xff1a; 输入&#xff1a;[1,2,2,3,4,4,5,6,7…
阅读更多...
2023年前端面试高频考点之 通信（渲染、http、缓存、异步、跨域）

2023年前端面试高频考点之 通信（渲染、http、缓存、异步、跨域）

目录 浏览器从输入url到渲染页面 过程⭐⭐⭐ Http和Https区别⭐⭐⭐ GET和POST发送请求⭐⭐⭐ 异同 http版本⭐⭐⭐ http状态码⭐⭐⭐ TCP⭐⭐⭐ 三次握手 四次挥手 流量控制&#xff08;滑动窗口机制&#xff09; 拥塞控制 keep-alive持久连接 TCP⭐⭐⭐ 三次握手…
阅读更多...
Revit中绘制多坡度的迹线屋顶和构件对齐

Revit中绘制多坡度的迹线屋顶和构件对齐

一、Revit中创建特殊多坡度的迹线屋顶 在我们的日常生活中可以见到一些建筑屋顶为偏欧式风格的屋顶&#xff0c;而有时候在做迹线屋顶时也需要作出如图一所示的效果&#xff0c;说明特殊的多坡度屋顶也是应用非常广泛的&#xff0c;那我们应该如何实现绘制呢? 1.要得到如上图所…
阅读更多...
Linux系统：安装及管理程序

Linux系统：安装及管理程序

安装及管理程序 一、linux源码包&#xff1a;1.源码包&#xff1a;2.二进制包&#xff1a;3.源码包的好处&#xff1a;4.源码包不足&#xff1a; 二、编译安装的过程&#xff1a;1.重点步骤&#xff1a; 三、挂载1.格式&#xff1a;2.挂载规则&#xff1a; 四、应用程序和系统命…
阅读更多...
使用Jmeter进行性能测试的这套步骤，涨薪2次，升职一次

使用Jmeter进行性能测试的这套步骤，涨薪2次，升职一次

项目背景&#xff1a; 我们的平台为全国某行业监控平台&#xff0c;经过3轮功能测试、接口测试后&#xff0c;98%的问题已经关闭&#xff0c;决定对省平台向全国平台上传数据的接口进行性能测试。 01、测试步骤 1、编写性能测试方案 由于我是刚进入此项目组不久&#xff0c…
阅读更多...
2023年专业连锁行业研究报告

2023年专业连锁行业研究报告

第一章 行业概况 专业连锁行业是指以连锁经营模式运营的公司&#xff0c;其主要业务涵盖零售、餐饮、酒店、医疗、教育等领域。这些公司通过规模化、标准化的经营模式和供应链管理&#xff0c;提供专业化、高质量的产品和服务。专业连锁行业在全球范围内蓬勃发展&#xff0c;并…
阅读更多...
LeetCode - 1 两数之和

LeetCode - 1 两数之和

目录 题目来源 题目描述 示例 提示 题目解析 算法源码 题目来源 1. 两数之和 - 力扣&#xff08;LeetCode&#xff09; 题目描述 给定一个整数数组 nums 和一个整数目标值 target&#xff0c;请你在该数组中找出和为目标值 target 的那 两个整数&#xff0c;并返回它们…
阅读更多...
Jmeter接口测试实战篇：10分钟学会Jmeter的用法

Jmeter接口测试实战篇：10分钟学会Jmeter的用法

一提到接口测试&#xff0c;通常大家会有这样的疑问&#xff1a;前端测试不是已经覆盖到各种业务逻辑了吗&#xff1f;为什么还要做接口测试&#xff0c;接口测试和前端测试是不是重复了&#xff1f;对于这个问题&#xff0c;可以从下面几个方面来解释&#xff1a; 什么是接口…
阅读更多...
架构之冷热分离

架构之冷热分离

本文依据《从程序员到架构师》阅读有感&#xff0c;记录书中案例并且结合作者工作经历进行分析。 当数据量过大&#xff0c;业务查询慢甚至导致数据库服务器CPU飙升&#xff0c;导致数据库宕机&#xff0c;影响用户体验。 场景&#xff1a; 1.客户两年多产生了近2000万的工单…
阅读更多...
k聚类简单实现（灰度分割，分黑白）

k聚类简单实现（灰度分割，分黑白）

加载图像&#xff1a; k聚类分割后图像&#xff0c;分成黑白两类&#xff0c;故意把结果黑色类染红&#xff0c;核对发现是正确的&#xff1a; 具体算法如下&#xff1a; float globu1 40; float globu2 180; public void k均值迭代法更新(int imgw, int imgh, byte…
阅读更多...
云晶-新一代云上操作系统的新定义，价值，应用范围

云晶-新一代云上操作系统的新定义，价值，应用范围

本文&#xff0c;从人类社会信息化到数字化的演变过程&#xff0c;以及当前的企业数字化现状&#xff0c;并回顾信息技术的几次革命来阐述总结操作系统的价值和意义。我们基于行业发展规律&#xff0c;重新定义了云晶-云上操作系统的架构和建设要点。并给出了大胆设想。 您也许…
阅读更多...
大模型部署实战（一）——Ziya-LLaMA-13B

大模型部署实战（一）——Ziya-LLaMA-13B

❤️觉得内容不错的话&#xff0c;欢迎点赞收藏加关注&#x1f60a;&#x1f60a;&#x1f60a;&#xff0c;后续会继续输入更多优质内容❤️ &#x1f449;有问题欢迎大家加关注私戳或者评论&#xff08;包括但不限于NLP算法相关&#xff0c;linux学习相关&#xff0c;读研读博…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023