【C语言】算法学习·Dijkstra算法详解

Dijkstra算法设计

Dijkstra算法简介

Dijkstra算法的基本思想

Dijkstra贪心策略

完美图解

伪代码详解

完整代码

算法解析及优化拓展

使用优先队列的完整代码

Dijkstra算法设计

Dijkstra算法简介

Dijkstra算法是解决**单源最短路径**问题的**贪心算法**
它先求出长度最短的一条路径，再参照该最短路径求出长度次短的一条路径直到求出从源点到其他各个顶点的最短路径。

Dijkstra算法的基本思想

首先假定源点为u，顶点集合V被划分为两部分：集合 S 和 V-S。初始时S中仅含有源点u，其中S中的顶点到源点的最短路径已经确定。
集合S 和V-S中所包含的顶点到源点的最短路径的长度待定，称从源点出发只经过S中的点到达V-S中的点的路径为特殊路径，并用dist[]记录当前每个顶点对应的最短特殊路径长度。

Dijkstra贪心策略

选择特殊路径长度最短的路径，将其连接的V-S中的顶点加入到集合S中，同时更新数组dist[]。一旦S包含了所有顶点，dist[]就是从源到所有其他顶点的最短路径长度。

（1）数据结构。设置地图的带权邻接矩阵为map[][]，即如果从源点u到顶点i有边，就令map[u][i]=<u,i>的权值，否则map[u][i]=∞；采用一维数组dist[i]来记录从源点到i顶点的最短路径长度：采用一维数组p[i]来记录最短路径上i顶点的前驱。
（2）初始化。令集合S={u}，对于集合V-S中的所有顶点x，初始化dist[i]=map[u][i],如果源点u到顶点i有边相连，初始化p[i]=u(i的前驱是u),否则p[i]=-1
（3）找最小。在集合V-S中依照贪心策略来寻找使得dist[j]具有最小值的顶点t,即dist[t]=min，则顶点t就是集合V-S中距离源点u最近的顶点。
（4）加入S战队。将顶点t加入集合S，同时更新V-S
（5）判结束。如果集合V-S为空，算法结束，否则转6
（6）借东风。在（3）中已近找到了源点到t的最短路径，那么对集合V-S中所有与顶点t相邻的顶点j，都可以借助t走捷径。如果dist[j]>dist[t]+map[t][j],则dist[j]=dist[t]+map[t][j]，记录顶点j的前驱为t，p[j]=t，转（3）。

我自己在这里理解就是，从u找到与它最近的点t，在从t找到与它最近的点j，在....按照这样持续下去，直到最后一个点这里我再通俗的解释下这个借东风的意思。源点为1，如果我们找到了距离源点最近的点2，且点2与3,4相连。这样，我们如果要倒3,4有两种方法：

1->2->3(4)
1->3(4)

这里我们就要判断是从1直接到3(4)快，还是经过2后快。假设<1,2>=2 / <2,3>=3 / <1,3>=4，根据上面的数据，我们第一次找最小找到的是2结点，如果我们直接把2替换掉1当做源点继续找下一个最近的点，这种方法是错的。

因为可以看出1->3只用4，而过2的话要用5。

完美图解

这里我就直接放图片了，书里的图不好画。但主要的是自己按照其流程过一遍，在草稿纸上自己画一遍。

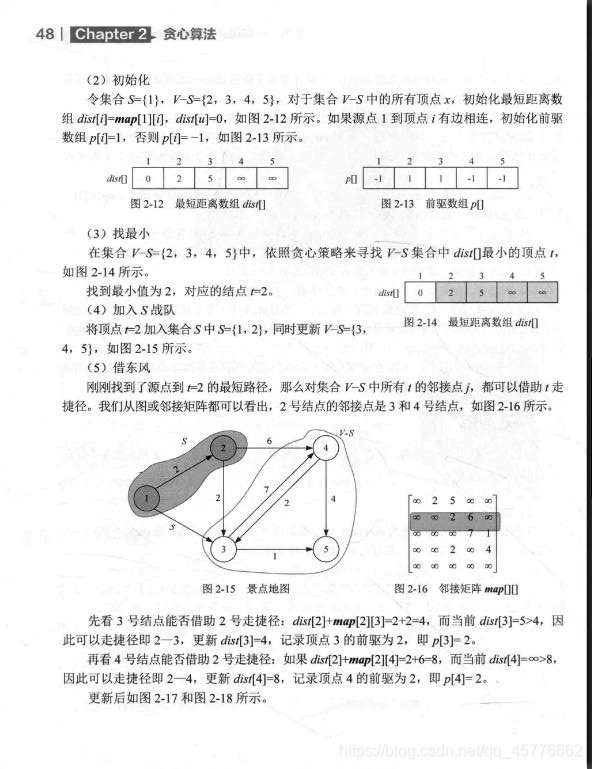
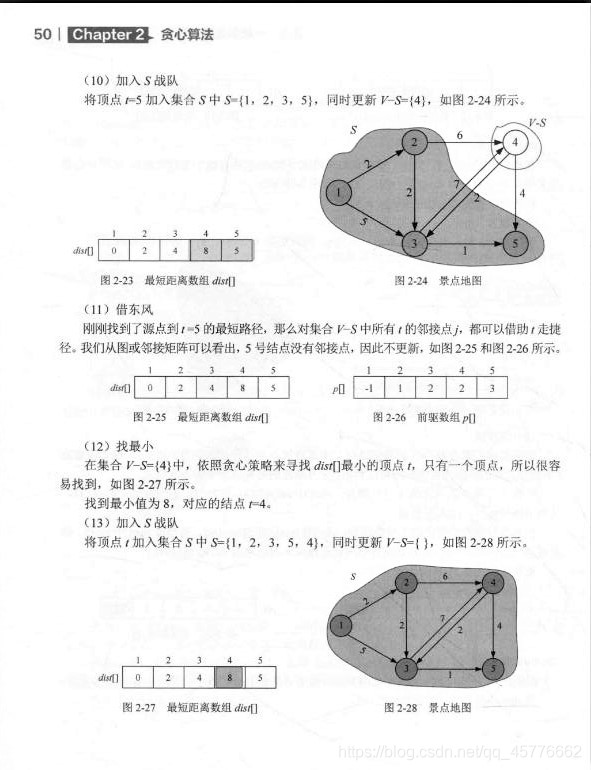
伪代码详解

跟着图解大致了解了一遍接下来就要上代码了，放心，代码不是一个完整的几十行的代码，全部按步骤划分好了的，这里方便大家粘贴。

/*
(1)数据结构
	n:城市顶点个数. m:城市间路线的条数. map[][]:地图对应的带权邻接矩阵. dist[]:记录源点u到某顶点的最短路径长度。
	p[]:记录源点到某顶点的最短路径上的该顶点的前一个顶点(前驱).flag[]：flag[i]=true说明顶点i已加入到集合S，否则该顶点属于集合V-S
*/
	const int N=100;//初始化城市个数，可修改
	const int INF=1e7;	//无穷大
	int map[N][N],dist[N],p[N],n,m;
	bool flag[N];

//(2)初始化源点u到其他各个顶点的最短路径长度，初始化源点u出边邻接点的前驱为u
	bool flag[n];//如果flag[i]=true,说明该顶点i已经加入到集合S；否则i属于集合V-S
	for(int i=1;i<=n;i++){
		dist[i]=map[u][i];	//初始化源点u到其他各个顶点的最短路径长度
		flag[i]=false;
		if(dist[i]==INF)
			p[i]=-1;	//说明源点u到顶点i无边相连，设置p[i]=-1
		else
			p[i]=u;	//说明源点u到顶点i有边相连，设置p[i]=u
	}
//(3)初始化集合S，令集合S={u},从源点u的最短路径为0
	flag[u]=true;//初始化集合S中，只有一个元素：源点u
	dist[u]=0;	//初始化源点u的最短路径为0，自己到自己的最短路径

//(4)找最小.在集合V-S中寻找距离源点u最近的顶点t,若找不到，则跳出循环;否则，将t加入集合S。
	int temp=INF,t=u;
	for(int j=1;j<=n;j++){//在集合V-S中寻找距离源点u最近的顶点t
		if(!flag[j] && dist[j]<temp){
			t=j;	//记录距离源点u最近的顶点
			temp=dist[j];
		}
	}
	if(t==u) return ;	//找不到t跳出循环
	flag[t]=true;	//否则，将t加入集合S
	
//(5)借东风。考察集合V-S中源点u到t的邻接点j的距离，如果源点u经过t到达j的路径更短，
//	则更新dist[j]=dist[t]+map[t][j],即松弛操作，并记录j的前驱为t;
	for(int j=1;j<=n;j++){//更新集合V-S中与t邻接的顶点到u的距离
		if(!flag[j] && map[t][j]<INF){//！flag[j]表示j在v-s集合中，map[t][j]<INF表示t与j邻接
			if(dist[j]>(dist[t]+map[t][j])){//经过t到达j的路径更短
				dist[j]=dist[t]+map[t][j];
				p[j]=t;	//记录j的前驱为t
			}
		}
	}	
//重复(4)~(5),知道源点u到所有顶点的最短路径被找到

完整代码

#include<bits/stdc++.h>
using namespace std;
const int N=100;	//城市个数可修改
const int INF=1e7;	//初始化无穷大为.......
int map[N][N],dist[N],p[N],n,m;	//n为城市个数，m为城市间路线的条数
bool flag[N];	//如果flag[i]=true,说明该顶点i已经加入到集合S；否则i属于集合V-S

void Dijkstra(int u){
	for(int i=1;i<=n;i++){//********>>>--1--<<<******//
		dist[i]=map[u][i];	//初始化源点u到其他各个顶点的最短路径长度
		flag[i]=false;
		if(dist[i]==INF)
			p[i]=-1;	//说明源点u到顶点i无边相连，设置p[i]=-1
		else
			p[i]=u;	//说明源点u到顶点i有边相连，设置p[i]=u
	}
	flag[u]=true;//初始化集合S中，只有一个元素：源点u
	dist[u]=0;	//初始化源点u的最短路径为0，自己到自己的最短路径
	for(int i=1;i<=n;i++){//********>>>--2--<<<******//
		int temp=INF,t=u;
		for(int j=1;j<=n;j++){//>>--3--<<在集合V-S中寻找距离源点u最近的顶点t
			if(!flag[j] && dist[j]<temp){
				t=j;	//记录距离源点u最近的顶点
				temp=dist[j];
			}
		}
		if(t==u) return ;	//找不到t跳出循环
		flag[t]=true;	//否则，将t加入集合S
		for(int j=1;j<=n;j++){//>>--4--<<更新集合V-S中与t邻接的顶点到u的距离
			if(!flag[j] && map[t][j]<INF){//！flag[j]表示j在v-s集合中，map[t][j]<INF表示t与j邻接
				if(dist[j]>(dist[t]+map[t][j])){//经过t到达j的路径更短
					dist[j]=dist[t]+map[t][j];
					p[j]=t;	//记录j的前驱为t
				}
			}
		}	
	}	
}

int main(){
		int u, v, w, st;
	system("color 0d");
	cout << "请输入城市的个数：" << endl;
	cin >> n;
	cout << "请输入城市之间的路线个数" << endl;
	cin >> m;
	cout << "请输入城市之间的路线以及距离" << endl;
	for(int i=1;i<=n;i++)//初始化图的邻接矩阵
		for (int j = 1; j <= n; j++)
		{
			map[i][j] = INF;//初始化邻接矩阵为无穷大
		}
	while (m--)
	{
		cin >> u >> v >> w;
		map[u][v] = min(map[u][v], w);	//邻接矩阵存储，保留最小的距离
	}
	cout << "请输入小明所在的位置：" << endl;
	cin >> st;
	Dijkstra(st);
	cout << "小明所在的位置：" << st << endl;
	for (int i = 1; i <= n; i++)
	{
		cout << "小明：" << st << " - " << "要去的位置：" << i << endl;
		if (dist[i] == INF)
			cout << "sorry,无路可达" << endl;
		else
			cout << "最短距离为：" << dist[i] << endl; 
	}
	return 0;
}

输入
请输入城市的个数：
5
请输入城市之间的路线个数
11
请输入城市之间的路线以及距离
1 5 2
5 1 8
1 2 16
2 1 29
5 2 32
2 4 13
4 2 27
1 3 15
3 1 21
3 4 7
4 3 19
请输入小明所在的位置：
5

输出
小明所在的位置：5
小明：5 - 要去的位置：1 最短距离为：8
小明：5 - 要去的位置：2 最短距离为：24
小明：5 - 要去的位置：3 最短距离为：23
小明：5 - 要去的位置：4 最短距离为：30
小明：5 - 要去的位置：5 最短距离为：0

因为我们在程序中使用了p[]数组记录了最短路径上每一个结点的前驱，所以我们可以增加一段程序逆向该最短路径上的城市序列。
void findpath(int u)
{
	int x;
	stack<int>s;
	cout << "源点为：" << u << endl;
	for (int i = 1; i <= n; i++)
	{
		x = p[i];
		while (x != -1)
		{
			s.push(x);
			x = p[x];
		}
		cout << "源点到其他各顶点的最短路径为：";
		while (!s.empty())
		{
			cout << s.top() << "--";
			s.pop();
		}
		cout << i << ";最短距离为：" << dist[i] << endl;
	}
}
只需要在主函数末尾调用即可

结果为：
源点为：5
源点到其他各顶点的最短路径为：5--1;最短距离为：8
源点到其他各顶点的最短路径为：5--1--2;最短距离为：24
源点到其他各顶点的最短路径为：5--1--3;最短距离为：23
源点到其他各顶点的最短路径为：5--1--3--4;最短距离为：30
源点到其他各顶点的最短路径为：5;最短距离为：0

算法解析及优化拓展

使用优先队列的完整代码

#include<queue>
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 100;//城市的个数可修改
const int INF = 1e7;//初始化无穷大为10000000
int map[N][N], dist[N], p[N], n, m;//n为城市的个数，m为城市间路线的条数
int flag[N];	//	如果flag[i]==true,说明顶点i已经加入到集合S；否则顶点i属于集合V-S

struct Node {
	int u, step;
	Node() {};
	Node(int a, int sp)
	{
		u = a, step = sp;
	}
	bool operator<(const Node& a)const {//重载 <
		return step > a.step;
	}
};

void Dijkstra(int st)
{
	priority_queue<Node>Q;//优先队列优化
	Q.push(Node(st, 0));
	memset(flag, 0, sizeof(flag));//初始化flag数组为0
	for (int i = 1; i <= n; ++i)
		dist[i] = INF;//初始化所有距离为无穷大
	dist[st] = 0;
	while (!Q.empty())
	{
		Node it = Q.top();//优先队列列头元素为最小值
		Q.pop();
		int t = it.u;
		if (flag[t])//说明已经找到了最短距离，该节点是队列里面的重复元素
			continue;
		flag[t] = 1;
		for (int i = 1; i <= n; i++)
		{
			if(!flag[i] && map[t][i]<INF)//判断与当前点有关系的点，并且自己不能到自己
				if (dist[i] > dist[t] + map[t][i])
				{
					//求距离当前点的每个点的最短距离，进行松弛操作
					dist[i] = dist[t] + map[t][i];
					Q.push(Node(i, dist[i]));//把更新后的最短距离压入队列中，注意：里面有重复元素
				}
		}
	}

}

int main()
{
	int u, v, w, st;
	system("color 0d");
	cout << "请输入城市的个数：" << endl;
	cin >> n;
	cout << "请输入城市之间的路线个数" << endl;
	cin >> m;
	cout << "请输入城市之间的路线以及距离" << endl;
	for (int i = 1; i <= n; i++)//初始化图的邻接矩阵
		for (int j = 1; j <= n; j++)
		{
			map[i][j] = INF;//初始化邻接矩阵为无穷大
		}
	while (m--)
	{
		cin >> u >> v >> w;
		map[u][v] = min(map[u][v], w);	//邻接矩阵存储，保留最小的距离
	}
	cout << "请输入小明所在的位置：" << endl;
	cin >> st;
	Dijkstra(st);
	cout << "小明所在的位置：" << st << endl;
	for (int i = 1; i <= n; i++)
	{
		cout << "小明：" << st << " ---> " << "要去的位置：" << i;
		if (dist[i] == INF)
			cout << "sorry,无路可达" << endl;
		else
			cout << " 最短距离为：" << dist[i] << endl;
	}
	return 0;
}

/*
请输入城市的个数：
5
请输入城市之间的路线个数
11
请输入城市之间的路线以及距离
1 5 2
5 1 8
1 2 16
2 1 29
5 2 32
2 4 13
4 2 27
1 3 15
3 1 21
3 4 7
4 3 19
请输入小明所在的位置：
5
小明所在的位置：5
小明：5 ---> 要去的位置：1 最短距离为：8
小明：5 ---> 要去的位置：2 最短距离为：24
小明：5 ---> 要去的位置：3 最短距离为：23
小明：5 ---> 要去的位置：4 最短距离为：30
小明：5 ---> 要去的位置：5 最短距离为：0
*/