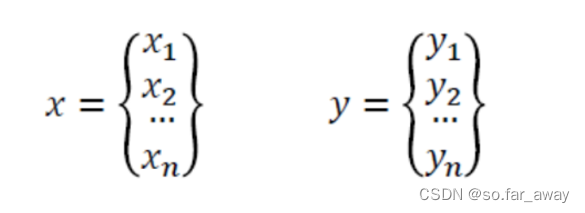支持向量机
- 算法概述
- 算法流程
- 线性分类
- 线性可分性
- 向量内积
- 硬间隔分类
- 软间隔SVM模型
- 非线性支持向量机
- 非线性的情况
- 非线性支持向量机
- 核函数
- SVM优点
- 算法步骤
- 线性可支持向量机的程序流程图
- SVM算法步骤
- 算法实例
- 有关数据集
- 利用Sklearn的datasets模块生成数据集
- 其他生成数据集的方法
- 线性支持向量机
- SVM分类算法
- SVM算法的应用
算法概述
支持向量机(SVM)是一种基于统计学习理论的监督学习方法。
支持向量机在各个领域内的模式识别问题中都有广泛应用,包括人脸识别、文本分类、笔迹识别等。
支持向量机解决不同类型的问题:
- 当训练数据线性可分时,通过硬间隔最大化,学习一个线性可分支持向量机;
- 当训练数据近似线性可分时,通过软间隔最大化,学习一个线性支持向量机;
- 当训练数据不可分时,通过使用核技巧以及软间隔最大化,学习一个非线性支持向量机。
算法流程
线性分类
- 给定一个特征空间上的训练数据集 T T T={ ( x i , y i ) ∣ i = 1 , 2 , . . , N (x_i,y_i)|i=1,2,..,N (xi,yi)∣i=1,2,..,N},其中 x i = [ x i 1 , x i 2 , . . . , x i n ] T ∈ X , y i ∈ Y = x_i=[x_{i1},x_{i2},...,x_{in}]^T∈X,y_i∈Y= xi=[xi1,xi2,...,xin]T∈X,yi∈Y={ -1,+1}, i = 1 , 2 , . . , N i=1,2,..,N i=1,2,..,N。
- x i x_i xi是训练数据集T的第i个实例, y i y_i yi是 x i x_i xi的类别标签。如果 y i = + 1 y_i=+1 yi=+1,则称 x i x_i xi为正例;反之如果 y i = − 1 y_i=-1 yi=−1,则称 x i x_i xi为负例。
- 一个线性分类器的学习目标就是要在这n维的数据空间中找到一个超平面,将所有的正例划分到超平面的一侧,将所有的负例划分到超平面的另一侧。
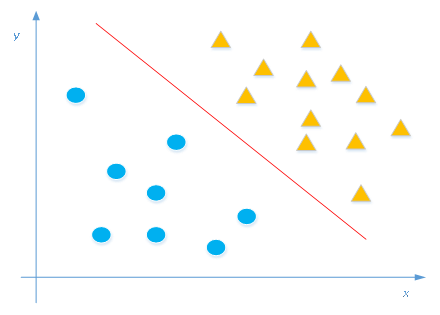
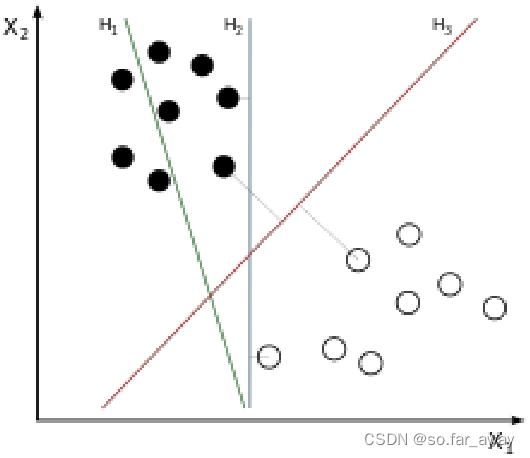
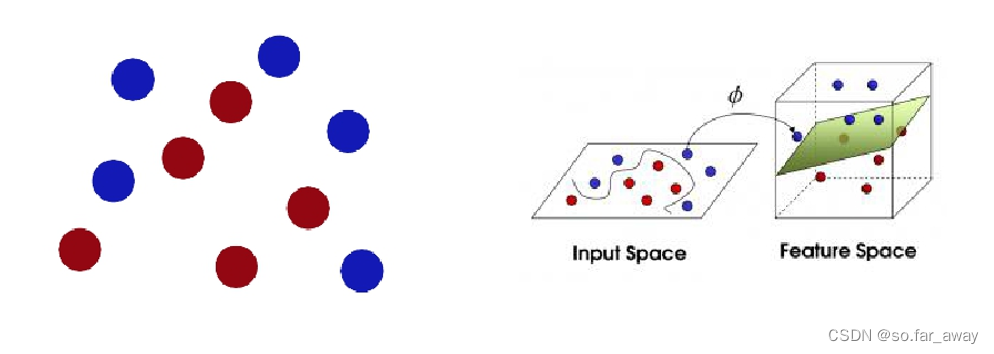
假设笛卡尔平面坐标系上有两类不同的数据,分别用三角形和圆形表示,其中的一个超平面就是中间的那条直线,如图所示。显然,这个超平面可将两类数据点分隔开来,超平面右上角数据点(三角形)所对应的分割结果全是-1,而在另一侧的数据点(圆形)全是+1。
线性可分性
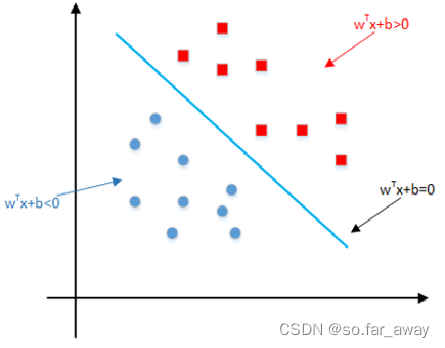
对于分离超平面: w T X + b = 0 w^TX+b=0 wTX+b=0,
可以将方点和圆点表示的两类不同数据完全分离开在该超平面的两侧,使其满足:
1. w T X + b > 0 w^TX+b>0 wTX+b>0的所有数据属于一类
2. w T X + b < 0 w^TX+b<0 wTX+b<0的所有数据属于另一类
称样本数据集为线性可分,称 w T X + b = 0 w^TX+b=0 wTX+b=0为分离超平面。
对于一个线性可分性的样本数据集,其分离超平面通常不止一个。
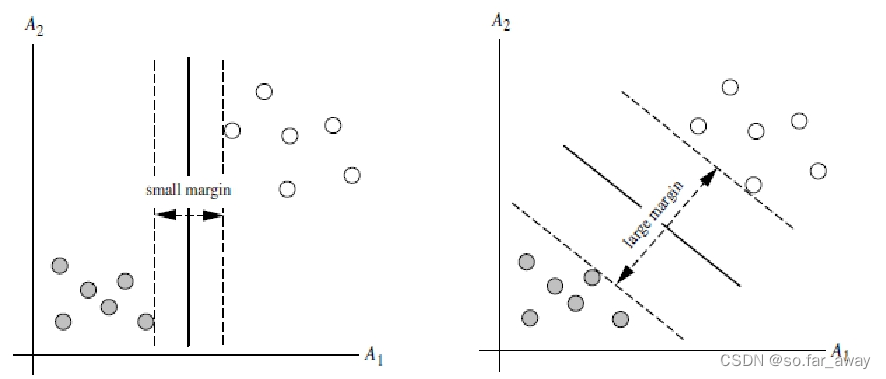
线性可分支持向量机提出了间隔最大化条件,以此来求得距离两个可分类的最佳超平面 。
注:SVM寻找区分两类的超平面,使边际最大。
向量内积
向量内积: x ⋅ y = x 1 y 1 + x 2 y 2 + . . . x n y n x\cdot y=x_1y_1+x_2y_2+...x_ny_n x⋅y=x1y1+x2y2+...xnyn
向量内积: x ⋅ y = ∣ ∣ x ∣ ∣ x\cdot y=||x|| x⋅y=∣∣x∣∣ ∣ ∣ y ∣ ∣ c o s ( θ ) ||y||cos(\theta) ∣∣y∣∣cos(θ)
范数:||x||= x ⋅ x \sqrt{x\cdot x} x⋅x= x 1 2 + x 2 2 + . . . + x n 2 \sqrt{x_1^2+x_2^2+...+x_n^2} x12+x22+...+xn2
当||x||≠0,||y||≠0时,可以求余弦相似度:
c o s θ = x ⋅ y ∣ ∣ x ∣ ∣ ∣ ∣ y ∣ ∣ cos\theta=\frac{x\cdot y}{||x||||y||} cosθ=∣∣x∣∣∣∣y∣∣x⋅y
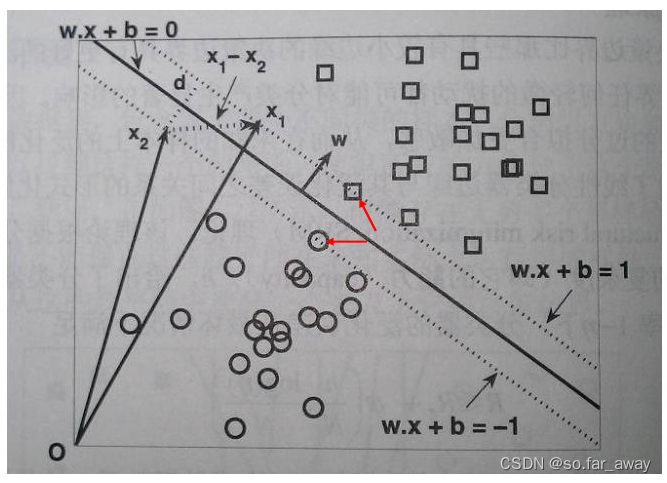
一些推导:
w ⋅ x 1 + b = 1 w\cdot x_1+b=1 w⋅x1+b=1
w ⋅ x 2 + b = − 1 w\cdot x_2+b=-1 w⋅x2+b=−1
w ⋅ ( x 1 − x 2 ) = 2 w\cdot (x_1-x_2)=2 w⋅(x1−x2)=2
||w|| ||( x 1 − x 2 x_1-x_2 x1−x2)|| cos( θ \theta θ) = 2
||w||*d=2
d= 2 ∣ ∣ w ∣ ∣ \frac{2}{||w||} ∣∣w∣∣2
转化为凸优化问题:
w ⋅ \cdot ⋅x+b≥1,则分类y=1
w ⋅ \cdot ⋅x+b≤1,则分类y=-1
即y(w ⋅ \cdot ⋅x+b)≥1
求d= 2 ∣ ∣ w ∣ ∣ \frac{2}{||w||} ∣∣w∣∣2最大值,也就是求min ∣ ∣ w ∣ ∣ 2 2 \frac{{||w||}^2}{2} 2∣∣w∣∣2
硬间隔分类
硬间隔分类的缺点:
1)只有数据线性分离才有效
2)对异常值太敏感
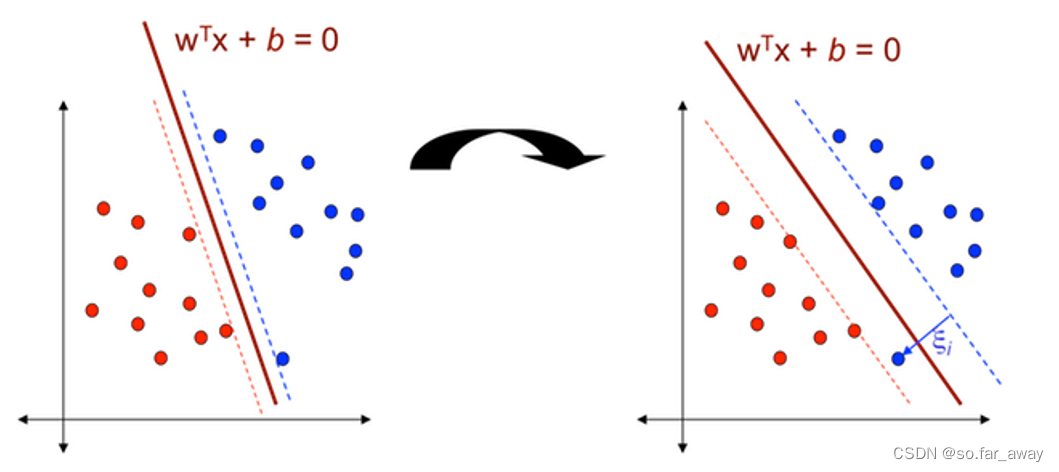
软间隔SVM模型
SVM模型:模型对S中任何训练样本都不能做出错误分类。
软间隔SVM模型:允许对少量训练样本出现分类错误。引入一个松弛变量 ξ i \xi_i ξi,将约束条件转化为:
y i ( w T X i + b ) ≥ 1 − ξ i y_i(w^TX_i+b)≥1-\xi_i yi(wTXi+b)≥1−ξi
ξ i \xi_i ξi的取值越大,模型对错误分类的容忍程度越高。
可得到如下优化求解软间隔SVM模型的目标函数:
m i n 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 n ξ i min\frac{1}{2}||w||^2+C\sum_{i=1}^{n}\xi_i min21∣∣w∣∣2+Ci=1∑nξi s . t . y i ( w T X i + b ) ≥ 1 − ξ i s.t.y_i(w^TX_i+b)≥1-\xi_i s.t.yi(wTXi+b)≥1−ξi
其中C>0是为惩罚因子。
非线性支持向量机
非线性的情况
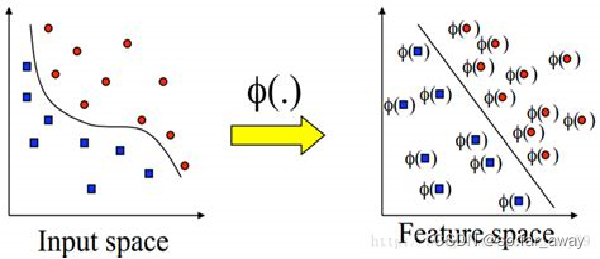
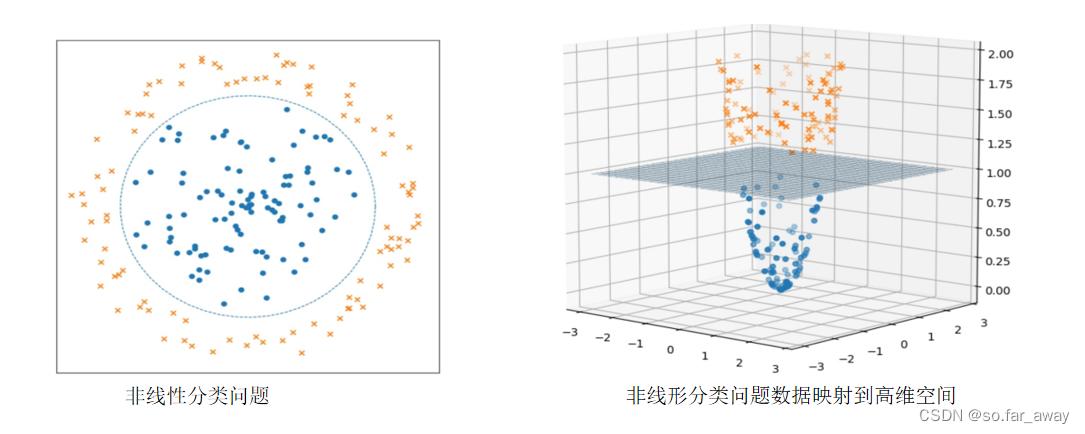
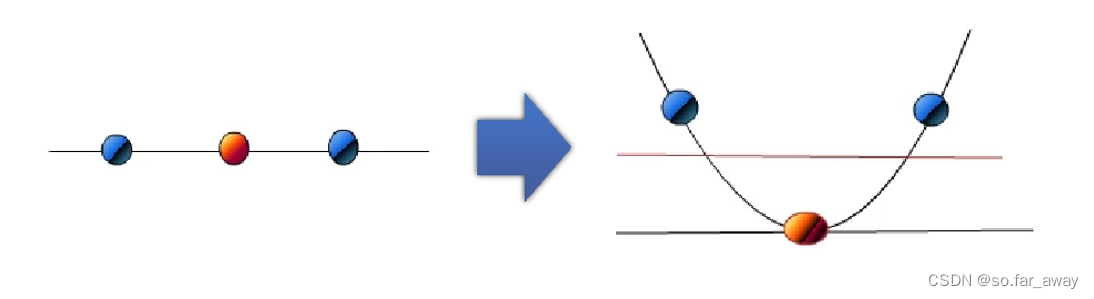
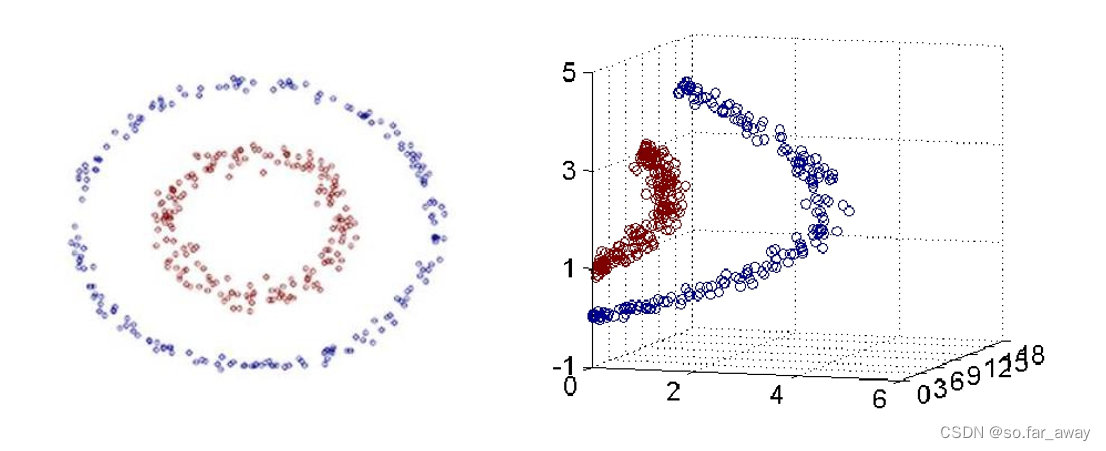
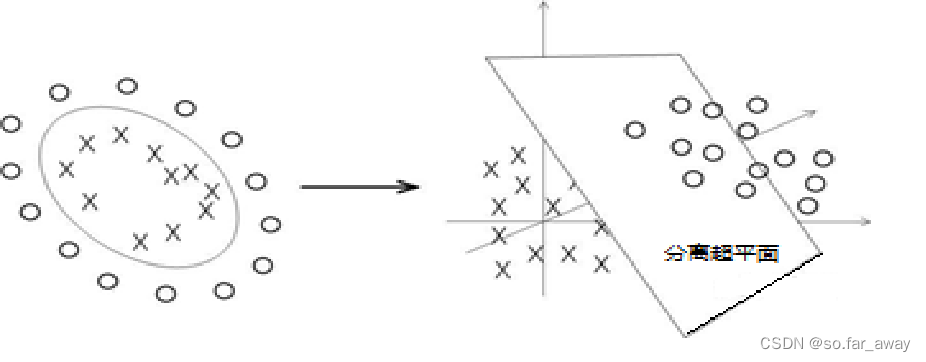
前面提到的支持向量机只能用于处理线性分类问题,但有时还会面对非线性分类问题。如下图的数据集,在空间中无法用一条直线(线性)将数据集中的正例和负例正确地分隔开,但可以用一条圆形曲线(非线性)分隔。这种使用非线性模型(超曲面)进行分类的问题称为非线性分类问题。
把低维空间的非线性问题映射到高维空间,变成求解线性问题。
非线性支持向量机
对于非线性的情况,支持向量机选择一个核函数,通过将数据映射到高维空间,从而解决原始空间中线性不可分的问题。
分类函数定义为:
f
(
x
)
=
∑
i
=
1
N
w
i
ϕ
i
(
x
)
+
b
f(x)=\sum_{i=1}^{N}w_iϕ_i(x)+b
f(x)=i=1∑Nwiϕi(x)+b
例如:
3维输入变量:X=(
x
1
,
x
2
,
x
3
x_1,x_2,x_3
x1,x2,x3)
转化到6维空间Z中去:
ϕ
1
(
X
)
=
x
1
,
ϕ
2
(
X
)
=
x
2
,
ϕ
3
(
X
)
=
x
3
,
ϕ
4
(
X
)
=
(
x
1
)
2
,
ϕ
5
(
X
)
=
x
1
x
2
,
a
n
d
ϕ
6
(
X
)
=
x
1
x
3
ϕ_1(X)=x_1,ϕ_2(X)=x_2,ϕ_3(X)=x_3,ϕ_4(X)=(x_1)^2,ϕ_5(X)=x_1x_2,and ϕ_6(X)=x_1x_3
ϕ1(X)=x1,ϕ2(X)=x2,ϕ3(X)=x3,ϕ4(X)=(x1)2,ϕ5(X)=x1x2,andϕ6(X)=x1x3
新决策超平面:d(Z)=WZ+b,其中W和Z是向量,这个超平面是线性的,解出W和b之后,并且带回原方程:
d(Z)
=
w
1
x
1
+
w
2
x
2
+
w
3
x
3
+
w
4
(
x
1
)
2
+
w
5
x
1
x
2
+
w
6
x
1
x
3
+
b
w_1x_1+w_2x_2+w_3x_3+w_4(x_1)^2+w_5x_1x_2+w_6x_1x_3+b
w1x1+w2x2+w3x3+w4(x1)2+w5x1x2+w6x1x3+b
=
w
1
z
1
+
w
2
z
2
+
w
3
z
3
+
w
4
z
4
+
w
5
z
5
+
w
6
z
6
+
b
w_1z_1+w_2z_2+w_3z_3+w_4z_4+w_5z_5+w_6z_6+b
w1z1+w2z2+w3z3+w4z4+w5z5+w6z6+b
核函数
虽然可以利用非线性变换处理非线性分类问题,但如果映射后的空间维度非常高,将导致进行非线性变换所使用的存储空间和计算资源开销过大,有时甚至是无法实现的。
但是利用核方法可以解决这个问题。核方法的核心思想是,利用核函数直接计算映射到空间后实例间的内积,以此代替先做映射再做内积。
常用的核函数有:
1)线性核函数(Linear Kernel)
2)多项式核函数(Polynomial Kernel)
3)径向基核函数(Radial Basis Function Kernel)又称高斯核
4)Sigmoid核函数(Sigmoid Kernel)
线性核函数
线性核函数(Linear Kernel)是最简单的核函数,主要用于线性可分的情况,表达式如下:
K
(
x
,
y
)
=
x
T
⋅
y
+
c
K(x,y)=x^T\cdot y+c
K(x,y)=xT⋅y+c
其中c是可选的常数。线性核函数是原始输入空间的内积,即特征空间和输入空间的维度是一样的,参数较少运算速度较快。
适用的情景是在特征数量相对于样本数量非常多时。
多项式核函数
多项式核函数(Polynomial Kernel)是一种非稳态核函数,适合于正交归一化后的数据,表达式如下:
KaTeX parse error: Undefined control sequence: \codt at position 19: …,y)=[a\cdot x^T\̲c̲o̲d̲t̲ ̲y+c]^d
其中a是调节参数,d是最高次项次数,c是可选的常数。
径向基核函数
径向基核函数(Radial Basis Function Kernel)具有很强的灵活性,应用广泛。
与多项式核函数相比参数较少,因此大多数情况下都有较好的性能。
径向基核函数类似于高斯函数,所以也被称为高斯核函数。
在不确定用哪种核函数时,可优先验证高斯核函数。
K
(
x
,
y
)
=
e
−
∣
∣
x
−
y
∣
∣
2
2
⋅
a
2
K(x,y)=e^{-{\frac{||x-y||^2}{2\cdot a^2}}}
K(x,y)=e−2⋅a2∣∣x−y∣∣2
a
2
a^2
a2越大,高斯核函数就会变得越平滑,此时函数随输入x变化较缓慢 ,模型的偏差和方差大,泛化能力差,容易过拟合。
a
2
a^2
a2越小,高斯核函数变化越剧烈,模型的偏差和方差越小,模型对噪声样本比较敏感。
Sigmoid核
Sigmoid核(Sigmoid Kernel)来源于MLP中的激活函数,SVM使用Sigmoid相当于一个两层的感知机网络,表达式如下:
K
(
x
,
y
)
=
t
a
n
h
(
a
⋅
x
T
⋅
y
+
c
)
K(x,y)=tanh(a\cdot x^T\cdot y+c)
K(x,y)=tanh(a⋅xT⋅y+c)
我们可以构造核函数使得运算结果等同于非线性映射,同时运算量要远远小于非线性映射。
核函数举例
假定定义两个变量:
x
=
(
x
1
,
x
2
,
x
3
)
;
y
=
(
y
1
,
y
2
,
y
3
)
x=(x_1,x_2,x_3);y=(y_1,y_2,y_3)
x=(x1,x2,x3);y=(y1,y2,y3)
①定义高维映射方程:
f
(
x
)
=
(
x
1
x
1
,
x
1
x
2
,
x
1
x
3
,
x
2
x
1
,
x
2
x
2
,
x
2
x
3
,
x
3
x
1
,
x
3
x
2
,
x
3
x
3
)
f(x)=(x_1x_1,x_1x_2,x_1x_3,x_2x_1,x_2x_2,x_2x_3,x_3x_1,x_3x_2,x_3x_3)
f(x)=(x1x1,x1x2,x1x3,x2x1,x2x2,x2x3,x3x1,x3x2,x3x3)
假设x=(1,2,3),y=(4,5,6)
f(x)=(1,2,3,2,4,6,3,6,9)
f(y)=(16,20,24,20,25,36,24,30,36)
求内积<f(x),f(y)>=16+40+72+40+100+180+72+180+324=1024
②定义核函数:
K(x,y)=(<x,y>)^2
K(x,y)=(4+10+18)^2=1024
同样的结果,但是使用核函数计算就容易得多
SVM优点
- 训练好的模型的算法复杂度是由支持向量的个数决定的,而不是由数据的维度决定的。所以SVM不太容易产生overfitting。
- SVM训练出来的模型完全依赖于支持向量(Support Vectors),即使训练集里面所有非支持向量的点都被去除,重复训练过程,结果仍然会得到完全一样的模型。
- 一个SVM如果训练得出的支持向量个数比较小,SVM训练出的模型比较容易被泛化。
算法步骤
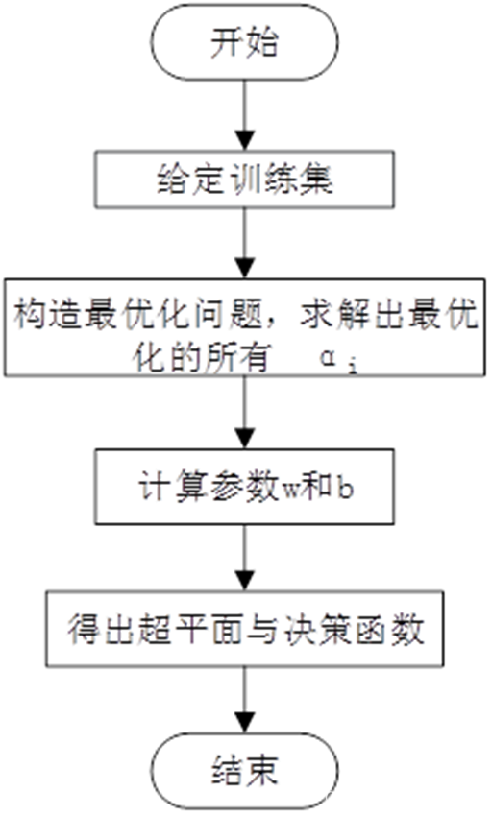
线性可支持向量机的程序流程图
SVM算法步骤
线性支持向量机的算法步骤如下:
1)给定训练集T=
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
.
.
.
,
(
x
n
,
y
n
)
,
y
=
−
1
,
1
{(x_1,y_1),(x_2,y_2),...,(x_n,y_n)},y={-1,1}
(x1,y1),(x2,y2),...,(xn,yn),y=−1,1
2)构造最优化问题
m
i
n
φ
(
α
)
=
1
2
∑
i
=
1
N
∑
j
=
1
N
α
i
α
j
y
i
y
j
(
x
i
⋅
x
j
)
−
∑
i
=
1
N
α
i
min\varphi(\alpha)=\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)-\sum_{i=1}^{N}\alpha_i
minφ(α)=21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)−i=1∑Nαi
3)计算参数w和b
w
=
∑
i
=
1
N
α
i
y
i
x
i
w=\sum_{i=1}^{N}\alpha_iy_ix_i
w=i=1∑Nαiyixi
b
=
y
i
−
x
i
⋅
∑
i
=
1
N
α
i
y
i
x
i
b=y_i-x_i\cdot \sum_{i=1}^{N}\alpha_iy_ix_i
b=yi−xi⋅i=1∑Nαiyixi
4)得出超平面与决策函数
w
⋅
x
+
b
=
0
w\cdot x+b=0
w⋅x+b=0分类决策函数如下
f
(
x
)
=
s
i
g
n
(
w
⋅
x
+
b
)
f(x)=sign(w\cdot x+b)
f(x)=sign(w⋅x+b)
算法实例
有关数据集
sklearn 的数据集有好多个种类:
- 自带的小数据集(packaged dataset):sklearn.datasets.load_
- 可在线下载的数据集(Downloaded Dataset):sklearn.datasets.fetch_
- 计算机生成的数据集(Generated Dataset):sklearn.datasets.make_
- svmlight/libsvm格式的数据集:sklearn.datasets.load_svmlight_file(…)
- 从买了data.org在线下载获取的数据集:sklearn.datasets.fetch_mldata(…)
利用Sklearn的datasets模块生成数据集
- 生成数据集:可以用来分类任务,可以用来回归任务,可以用来聚类任务……
- 用于分类任务和聚类任务的:这些函数产生样本特征向量矩阵以及对应的类别标签集合
- make_blobs:多类单标签数据集,为每个类分配一个或多个正态分布的点集,对每个类的中心和标准差有很好的控制
from sklearn.datasets.samples_generator import make_blobs
sklearn.datasets.samples_generator.make_blobs(n_samples=100, n_features=2, centers=3, cluster_std=1.0, center_box=(-10.0, 10.0), shuffle=True, random_state=None) - 返回结果:
X:[n_samples,n_features]大小的特征矩阵
y:[n_samples]大小的标签数据矩阵,对应特征矩阵的每一行
其他生成数据集的方法
- make_classification:多类单标签数据集,为每个类分配一个或多个正态分布的点集,提供了为数据添加噪声的方式,包括维度相关性,无效特征以及冗余特征等
- make_gaussian-quantiles:将一个单高斯分布的点集划分为两个数量均等的点集,作为两类
- make_hastie-10-2:产生一个相似的二元分类数据集,有10个维度
- make_circles和make_moons:产生二维二元分类数据集来测试某些算法的性能,可以为数据集添加噪声,可以为二元分类器产生一些球形判决界面的数据
线性支持向量机
支持向量机是一种可构造唯一决策面的线性分类器,所构造的决策面能够将其到与其最近的训练实例(支持向量)的距离最大化。
sklearn提供了线性分类支持向量机(LinearSVC)的实现,其函数原型为:
class sklearn.svm.LinearSVC(penalty=’l2’, loss=’squared_hinge’, dual=True, tol=0.0001, C=1.0, multi_class=’ovr’, fit_intercept=True, intercept_scaling=1, class_weight=None, verbose=0, random_state=None, max_iter=1000)
- penalty:字符串,默认参数值为“l2”。惩罚类型,指定“l1”或“l2”。
- loss:字符串,可选“hinge”或“squared hinge”,默认参数值为“squared hinge”。 损失函数。
- C:浮点数。惩罚参数。C参数决定SVM分类器的边距宽度。C的值越大分类器越严格,因此边距宽度小。对于较大的C值,如果该超平面更好地将所有训练点归类正确,则该模型将选择较小边距的超平面。相反,C的非常小的值将导致模型寻找更大的边距分离超平面,即使这个超平面错误的分类了更多的点。
- multi_class:字符串。多类分类问题的策略,取值可选“ovr”“crammer_singer”之一,默认参数值为“ovr”。“ovr”采用one-vs-rest分类策略;“crammer_singer”采用多类联合分类策略。
- fit_intercept:布尔值。如果为True,则计算截距,即决策函数中的常数项;否则忽略截距。
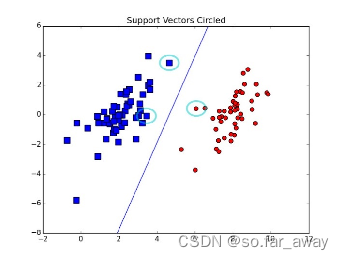
示例:首先创建可以分离的样本数据集(假定二分类),然后使用sklearn所提供的线性支持向量机(LinearSVC)方法对其进行分类,求取一个支持向量集并绘图,具体代码如下。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import LinearSVC
from sklearn.datasets import make_blobs
#创建随机分布的 可以分离的400个样本点
X,y=make_blobs(n_samples=400,centers=2,random_state=32)
#创建LinearSVC对象
clf=LinearSVC(C=10)
clf.fit(X,y)
plt.scatter(X[:,0],X[:,1],c=y,s=30,cmap=plt.cm.Paired)
#画出决策函数
ax=plt.gca()
xlim=ax.get_xlim()
ylim=ax.get_ylim()
#网格化评价模型
xx=np.linspace(xlim[0],xlim[1],30)
yy=np.linspace(ylim[0],ylim[1],30)
YY,XX=np.meshgrid(yy,xx)
xy=np.vstack([XX.ravel(),YY.ravel()]).T
Z=clf.decision_function(xy).reshape(XX.shape)
#画分类边界
ax.contour(XX,YY,Z,colors='k',levels=[-1,0,1],alpha=0.5,linestyles=['--','-','--'])
plt.title('Maximum margin using LinearSVC')
plt.show()
实验结果:

SVM分类算法
Scikit-learn中实现SVM分类算法的SVC类如下:
sklearn.svm.SVC(C=1.0, kernel='rbf', degree=3, gamma='scale', coef0=0.0, shrinking=True,probability=False, tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape='ovr', break_ties=False, random_state=None)
其主要参数为:
1)C:惩罚系数。数据类型为浮点型,值严格大于0,常选用C=1.0。
2)kernel:核函数。值有linear、poly、rbf、sigmoid、precomputed或可调用核函数等参数可选。若不指定该参数值,则自动使用默认参数值rfb。
3)degree:多项式核函数阶数。数据类型为整型,若不指定该参数值,则自动使用默认参数值3。仅当kernel参数选用poly时有效,其他核函数下该参数无效。
4)gamma:指定核函数的系数。数据类型为浮点型或可选scale、auto。当核函数参数kernel为poly、rbf和sigmoid时,指定系数。若不指定该参数值,则自动使用默认参数值scale。
5)coef0:核函数自由项。数据类型为浮点型,若不指定该参数值,则自动使用默认参数值0.0。只有当核函数kernel参数为poly和sigmoid时有效。
6)shrinking:是否使用缩小的启发方式。数据类型为布尔型,若不指定该参数值,则自动使用默认参数值True。
7)probability:是否启用概率估计。数据类型为布尔型,若不指定该参数值,则自动使用默认参数值False。这必须在调用fit()之前启用,并且会使fit()方法速度变慢。
8)tol:停止训练的误差精度。数据类型为浮点型,若不指定该参数,则使用默认参数值0.001。
9)cache_size:指定训练所需要的内存。数据类型为浮点型,以MB为单位,若不指定该参数,则使用默认参数值200MB。
10)class_weight:样本数据中每个类的权重。数据类型为字典、balanced或None,若不指定该参数值,则自动使用默认参数值None。
11)verbose:是否启用详细输出。数据类型为布尔型,若不指定该参数值,则自动使用默认参数值False。
12)max_iter:最大迭代次数。数据类型为整型,若不指定该参数值,则自动使用默认参数值-1,表示不限制迭代次数。
13)decision_function_shap:指定决策函数的形状。有ovo、ovr参数值可选,若不指定该参数,则自动使用默认参数值ovr。
14)random_state:随机种子的设置。若不指定该参数值,则自动使用默认参数值None,即使用当前系统时间作为种子,每次随机结果不同。
其主要属性为:
- support_:支持向量的下标。
- support_vectors_:支持向量集。
- n_support:每个分类的支持向量数。
- dual_coef_:分类决策函数中每个支持向量的系数。
- coef_:每个特征的系数,仅在线性核下有效。
- intercept_:决策函数中常数项。
SVM算法的应用
SVC算法中不同参数对分类效果的影响:
1)C:惩罚系数,即对误差的宽容度。
C越大,说明越不能容忍出现误差,容易过拟合; C越小,越容易欠拟合。
需要对C进行选择,以便在平滑的决策边界和分类正确性之间进行平衡。
2)gamma:指定核函数的系数。
隐含地决定了数据映射到新的特征空间的分布: gamma值越大,支持向量越少。