对偶理论是研究线性规划中原始问题与对偶问题之间关系的理论,主要研究经济学中的相互确定关系,涉及到经济学的诸多方面。产出与成本的对偶、效用与支出的对偶,是经济学中典型的对偶关系。
对偶理论中最有力的武器是影子价格,影子价格来源于资源配置的最优化,是在最优决策下对一种资源效用价值的估计,它真实反映了资源在经济结构中对目标函数值的影响和贡献。如何为公司做出最合适的线性规划模型,并且利用模型中的影子价格指导公司周转再投资,已经成为众多企业管理者面临的重要问题。
本期,小编选取对偶理论的经济意义、资源使用问题、资源配置问题、企业挖潜问题和资源重新分配问题进行详细讲解。
#1 对偶理论的经济意义
问题描述:
某企业生产需要m种资源,记为A1,····,Am,其拥有量分别为b1,····,bm,现在用来生产n种产品,记为B1,····,Bn,产品Bj的每个单位的利润为cj,又生产每单位的Bj需要资源Ai的量为aij,j=1,····,n,i=1,····,m。若企可购买资源,企业如何安排生产,使利润最大?
模型求解:
设xj表示Bj产品的数量。
wi表示对偶问题的自变量。

在对偶问题中引入的新变量仅是z'和wi,因为原问题和对偶问题的最优值相等,故有z=z'。因而z'的量纲仍是利润。
即
![]()
为了保持两侧量纲一致,易分析出对偶变量wi,的量纲为:
wi=利润/第i资源单位数
问题解析:
wi为第i种资源从原来的量bi增加一个单位时,目标函数最优值的增量。这个结果在经济学上的含意是重要的。当已知线性规划问题的最优解时,它只告诉了企业管理者在目前情况下如何最好的利用它们的资源,以获取最大利润。
而优秀的管理者都希望能改善现状,以获取更多的利润。对偶变量就提供了这一重要信息。例如,若原问题的对偶问题的最优解中有w3=9,这意味着第3种资源每增加一个单位,可使目标函数的最优值增加9个单位,而w1=0时,说明第1种资源的增加不会使总利润提高,这给管理者提供了获取更大利润的有用信息。

#2 资源使用问题
问题描述:
假设某公司生产甲乙两种产品,这两种产品都需要三种资源:设备、原料、燃料。现在已知生产部门提供了如下的数据:
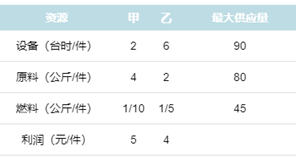
试问该公司每天应生产甲乙两种产品各多少件时,才能使盈利最多?
如果公司打算通过联合转产或者对外加工来提高经济效益,该公司在何种价格下所获得的盈利不少于最大利润?
模型求解:
设每天生产甲产品x1件,乙产品x2件,公司获利Z元;设y1,y2,y3分别表示设备、原料和燃料的每单位的估价,转产后的总效益为G元。

问题解析:
“影子价格”是线性规划对偶问题的最优解。这就是说,设备的影子价格为0.3元,原料的影子价格为1.1元,燃料的影子价格为零。当设备增加每个台时所获得的利润等于或大于0.3元,原料增加每公斤所获得的利润等于或大于1.1元时,可以转产或对外加工,否则不考虑转产或对外加工。燃料的影子价格为零,说明增加燃料的供应量并不能提高总的经济效益。
公司的决策者可以根据“影子价格”的高低来决定是否联合转产或对外加工。

#3 资源配置问题
问题描述:
假设某公司生产甲乙两种产品,这两种产品都需要三种资源:设备、原料、燃料。现在已知生产部门提供了如下的数据:
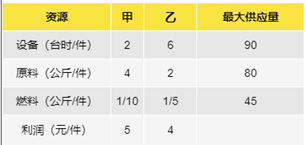
企业应该优先配置哪些资源,使得有限资源的情况下得到最大的效益。
模型求解:
设生产x1件甲产品,x2件乙产品。建立如下数学模型。

求解结果为:x1=15,x2= 10, Z=115
由结果可知,在现有设备、原料和燃料的供应条件下,公司每天要生产15件甲产品,10件乙产品,可获得的最大盈利为115元。
问题解析:
当设备从90台时增加到91台时的时候,通过公式
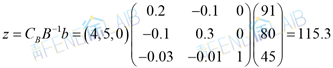
得公司总的经济效益为115.3。这就是说企业总的经济效益从115元增加到115.3元,这个增加数值0.3元,正是此种资源的影子价格。
同理,当燃料从45公斤增加到46公斤时,企业总的经济效益不增加,即影子价格为零,表明此种资源在现有的条件下有剩余,增加燃料不能提高效益。
原料增加一个单位时,即从80公斤增加到81公斤时,总的经济效益增加的数值也正是它的影子价格,即0.1。
因此企业应优先配置设备,其次是燃料。
综上可得,影子价格大于零,表明此种资源稀缺;影子价格越大,表明此种资源越稀缺,增加此种资源所带来的经济效益就越大;这就是说企业的管理者可以根据影子价格的大小,确定优先配置的资源种类,抓住重点突破影响企业利润增长的瓶颈。

#4 企业挖潜问题
问题描述:
汉威公司有甲、乙两个厂子,其中甲厂生产A1、A2、A3三种产品,需要使用的机械台时原材料、电及技术服务均是有限的,分别为120小时、160吨、80千瓦和120小时,每生产单位产品A1、A2、A3分别需要消耗机械台时2、2、3小时,消耗原材料4、0、6吨,消耗电1、2、2千瓦,消耗技术服务0、4、3时,单位产品A1、A2、A3所能提供的利润分别为2、3、5万元。企业管理者如何通过内部挖潜和革新来降低消耗或者及时补充该资源,以保证企业能够在原有技术条件下获得最大的收益。
模型求解:
设xj表示Aj产品的数量。
yj表示对偶问题的自变量。

原问题的最优解求解结果为:x1 =10,x2 = 15,x3 =20,f =165,即甲厂的最优分配方案为生产A1、A2、A3三种产品各10、15、20个单位,可获最大利润165万元。
求解得到对偶问题的解为0、0.4375、0.25、0.625,也就是说四种资源的影子价格分别为0、0.4375、0.25、0.625。
问题解析:
甲厂机械台时的影子价格为0,说明机械台时在资源的最优分配方案中有剩余,即机械台时再增加或适当减少总利润都不变,因此甲厂的决策者可考虑将机械台时租赁或转让,其它资源不变。通过对资源机械台时的可用量,即参数b1的灵敏度分析,可以得知多少的机械台时可以有偿转让,这部分在之后的灵敏度分析是进行详细讲解。
另外甲厂技术服务的影子价格为0.625,它是四种资源中影子价格的最大者,这说明技术服务最紧缺,应首先考虑增加技术服务,如果甲厂由某种方式能增加技术服务,则公司的总利润就会增加。

#5 资源重新分配问题
问题描述:
汉威公司有甲、乙两个分公司,甲公司的生产情况在确定企业挖潜问题中有所提到,乙公司的生产生产B1、B2、B3三种产品,也需要使用机械台时、原材料、电和技术服务四种资源,每生产单位产品B1、B2、B3需要消耗机械台时3、1、2小时,消耗原材料1、2、4吨,消耗电2、2、1千瓦,消耗技术服务1、1、2小时,单位产品B1、B2、B3所能提供的利润分别为4、2、3万元,另外总公司共拥有机械台时300小时,原材料260吨,电293千瓦,技术服务208小时。总公司应如何调整四种资源在甲、乙两厂之间的比例才能提高公司的经济效益呢?
模型求解:
设xj表示Bj产品的数量。
yj表示对偶问题的自变量。

原问题的最优解求解结果为: x1 =52,x2 = 24,x3 =0,f =256,即乙厂的最优分配方案为生产B1、B2、B3三种产品各52、24、0个单位,可获最大利润256万元。
求解得到对偶问题的解为1.2、0.4、0、0,也就是说四种资源的影子价格分别为1.2、0.4、0、0。
问题解析:
由于乙厂比甲厂机械台时的影子价格大,说明要将甲厂的部分机械台时适当地调给乙厂,整个公司的利润会增加。另外甲厂比乙厂另外三种资源的影子价格都大,说明将乙厂的另外三种资源适当的调给甲厂,整个公司的利润也会增加。
由灵敏度分析得知甲、乙厂原问题在保持各自最优基不变的条件下,即
B-1b≥0
可得参数bi的变化范围,即四种资源的变化范围是:
甲厂: b1≥110,80≤b2≤240,220/3≤b3≤ 260/3,80≤b4≤400/3。
乙厂: 50≤b1≤200,60≤b2≤110,b3≥152,b4≥76。
甲、乙厂原有资源为:
甲厂: b1=120,b2=160,b3=80,b4=120。
乙厂: b1=180,b2=100,b3=213,b4=88。
因此由甲厂调给乙厂min{120-110,200-180}=10小时的机械台时,同时由乙厂调给甲厂min{100-60,240-160}=40吨原材料,min{213-152,260/3-80}=20/3千瓦电,min{88-76,400/3-120}=12小时技术服务。
此时总公司的总利润增加:
(1.2-0)×10+(0.4375-0.4)×40+(0.25-0)×20/3+(0.625-0)×12=22.7万元。
在本案例中运用了灵敏度分析的知识,得到了通过重新分配甲、乙厂的资源,总公司的总利润的实际增加额。可以看出灵敏度分析也是经济学中的一大利器,灵敏度分析会在接下来的推文中全部传授给大家,敬请期待。