x.1 Data Manipulation

数据操作。在Pytorch中常用的数据操作如下：

对于张量，即torch.Tensor类型的数据，你的任何操作都要把他想象成一个指针，因为等于运算符a=b，会将b的张量内存地址赋值给a。

'''torch.Tensor类型的基本使用'''

# 集中常见的初始化torch.Tensor的方法

import torch

# one dimension
x = torch.arange(12)
print(x, x.shape, x.dtype, x.numel(), )

# reshape
y = x.reshape(3, -1)
print(y)

# multi dimensions
a = torch.zeros((2, 3, 4))
b = torch.ones((2, 3, 4))
c = torch.randn((2, 3, 4))
d = torch.tensor([[2, 2, 2], [3, 3, 3]])
print(a, '\n', b, '\n', c, '\n', d)


# 运算符: 运算符的运算是按照元素进行的
e = a + b

# concat 拼接，指定拼接的dim
f = torch.cat((a, b), dim=0)
print(f)

# sum计算求和统计量
g = b.sum()
print(g)

# 判断位置是否相同，常用于做mask
k = a == b
print(k)

# 广播机制，在进行四则运算的时候，当矩阵形状不同时，会先扩展为形状相同再进行计算。但是很多情况下我并不知道怎么使用。常用的是矩阵加一个标量。
h = torch.arange(6).reshape(3, 2)
i = torch.arange(2).reshape(1, 2)
print(h)
print(i)
j = h+i
print(j)

# 切片和索引。同python中的list使用
a[0, 0, 0:3] = 7
print(a)

# 我们使用id()进行内存定位。Y=[expresion Y]会重新分配Y的内存；Y[:]=和Y+=都不会重新分配内存。建议多用后者，这样做可以减少内存开销。
before = id(y)
y = y + 1
print(id(y) == before)

before = id(y)
y += 1
print(id(y) == before)

before = id(y)
y[:] = y + 1
print(id(y) == before)

# 类型转换
l = x.numpy()
m = torch.tensor(l)
print(type(l), type(m))

# 提出tensor 的标量
n = torch.tensor([[1.]])
print(type(n.item()), type(float(n)))

x.2 Data Preprocessing

数据预处理。数据预处理常常使用Pandas库。

常用操作如下：

'''pandas的基本使用'''

import pandas as pd
import torch

# 存储数据/读取数据
import pandas as pd
data_file = "./_.csv"
data = pd.read_csv(data_file)
print(data)
data.to_csv(data_file)

# 创建Pandas DataFrame
DF_NAME = [
    "channel",
    "position",
    "dir_name",
]
# 创建空DataFrame
df_rows_num = 10
df = pd.DataFrame(
    data=None, 
    index=range(df_rows_num),
    columns=DF_NAME,
)
print(df)

# 新增新的一行数据
# add one row - method 1: generage a dictionary, then using .loc[]  || recommanded ||
df_one_row_dict = {
    "channel":  "retardance",
    "position": 4,
    "dir_name": "None",
}
df.loc[0, :] = df_one_row_dict
# add one row - method 2: generate one dataframe, then using concat.
df_one_row_dict = {
    "channel":  ["retardance"],
    "position": [4],
    "dir_name": ["None"],
}
df_one_row = pd.DataFrame(df_one_row_dict)
df = pd.concat([df, df_one_row], axis=0)
print(df)

# 筛选数据
inputs, targets = data.iloc[:, 0:2], data.iloc[:, 2]
inputs = pd.get_dummies(inputs, dummy_na=True)
print(inputs)

# 类型转换 - 转为numpy
numpy_data = df.to_numpy()
print(numpy_data)
# 转为tensor: 用.values只取值（将index剔除）；用.astype("float64")指定ndarray的数据类型。
df_position = df.loc[:, "position"]
df_position = df_position.dropna(axis=0, how="all")
print(df_position)
torch_data = torch.tensor(df_position.values.astype("float64"), dtype=torch.float64)    # ndarray转换类型
print(torch_data)

x.3 Linear Algebra

在线性代数这个阶段，我们首先需要知道scalars标量, vectors向量, matrices矩阵, tensors张量以及它们的基本操作例如reduction降维, non-reduction sum非降维求和, dot products点积, matrix-vector products矩阵向量积, Matrix-Matrix Multiplication矩阵-矩阵乘法, Norms范数。

从scalars到tensors是升维的过程，其中scalar是0维张量，vector是1维，matrix是2维，而tensor是多维。例如想象立方体，除了长宽还有一个维度用来表示厚度；又如JPG图片的解释形式，三个维度表示R, G, B。

对于张量，它的数加a是各元素都加a，数乘同理。而对于两个相同shape的张量，张量相加就是逐元素相加，hadamard product哈马达积就是逐元素相乘（逐元素指的是对应位置的元素）。

对于张量的降维是本章难点，首先维度的排列是从第0维到第n维，例如[[]]具有两维度，从外层至内层依次是第0维，第1维。而用来降维的函数有sum()和mean()，其中可以指定维度，如axis=0即在第0维上降维squeeze掉，如下：

巧记：在哪个维度进行sum，即将该维度上所有元素相加，如[[0, 1], [1, 2]]在0维度相加，即将0维所有元素[0, 1]和[1, 2]相加，最终变成了[1, 3]。

点积即投影，对应元素相乘再相加。矩阵-向量乘和矩阵-矩阵乘即数学上的矩阵乘法。

范数常见于描述距离，常见有L1范数MAE，L2范数MSE，Lp范数的表达如下：

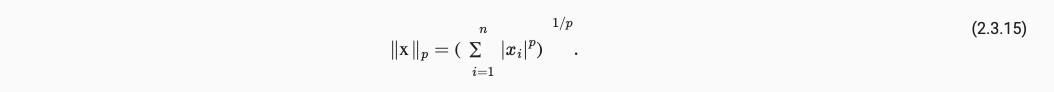
附录该小节代码：

'''一些数学知识，关于线性代数的'''

# 统计学中一行数据叫一个样本，一列数据叫一个特征feature，最后一列往往是标签label

import torch

# 标量 - 指0维数据
a = torch.tensor(1.)
print(a)

# 向量 - 指1维数据
b = torch.arange(12)
print(b, b[7], len(b), b.shape)

# 矩阵 - 指多维数据
c = torch.arange(12).reshape(3, 4)
print(c)
# 矩阵转置
# d = torch.transpose(c, 1, 0)
d = c.transpose(1, 0)
print(d)

# 两个矩阵的哈马达积用*
e = torch.arange(12, dtype=torch.float32).reshape(3, 4)
# f = e         # id 相同
# f = e.clone() # id 不同
f = e + 0       # id 不同
print(id(e) == id(f))
g = f * e   # 哈马达积
print(g)

# 矩阵求和sum(); 求均值mean(); 
# 你除了知道这两个API的作用外，你还应该知道这两个函数是用来降维的。
h = g.sum(axis=[0, 1])
i = g.mean(axis=[0, 1])
print(h, i)

# 两个向量的点积用.dot()
j = torch.ones(4, dtype=torch.float32)
k = j.clone()
l = j.dot(k)
print(l)

# 矩阵-向量乘法用.mv
m = torch.arange(12).reshape(6, 2)
n = torch.ones(2, dtype=torch.long) # shpae=[2, 1, 1, 1, ...]补全是往后补1
print(n)
o = m.mv(n)
print(o)

# 矩阵-矩阵乘法用.mm
p = m.transpose(1, 0)
q = m.mm(p)
print(q)

# 向量二范数（又叫L2范数）就是平方和的平方根, 用norm()二范数的英文
r = torch.tensor([3., 4.])
s = r.norm()
print(s)

# 向量一范数（又叫L1范数）就是绝对值的和
t = r.abs().sum()
print(t)

# 矩阵的Frobenius范数类似向量的二范数，就是各个元素平方和的平方根
u = torch.randn(3, 4)
v = u.norm()
print(v)

x.4 Calculus

在微积分中最重要的就是基于链式法则的偏导数计算，将求得的偏导连起来就是梯度方向，梯度即fx下降最快的反方向，如下：

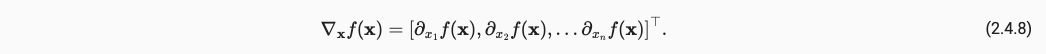
引入微积分的例子只是说明在Pytorch中的tensor是会自动微分的，当你调用y.backward()时候会自动计算y的梯度并更新模型的存储梯度信息的矩阵，以至于在后面的optimizer.step()中更新模型的存储权重信息的矩阵。

关于微积分的代码部分：

'''关于微积分的学习'''

# 我们往往使用python进行参数的训练。在使用c/c++将模型部署到硬件/软件上。

# 微分。用导数定义求导。
def f(x):
    return 3 * x ** 2 - 4 * x

def numerical_lim(f, x, h):
    return (f(x + h) - f(x)) / h

h = 0.1
for i in range(5):
    print(f'h={h:.5f}, numerical limit={numerical_lim(f, 1, h):.5f}') 
    h *= 0.1


# torch或者tf相比较于numpy好用的地方有两点， 1. 分别是可以传入GPU进行计算 2. 可以自动微分（automatic differentiation）
# 其中torch会根据搭建的模型构建一个计算图(computational graph)来跟踪计算; 而反向传播(backpropagate)则是根据计算图计算每个参数的偏导数。
import torch

x = torch.arange(4.)
x.requires_grad_(True)  # 对x开启梯度跟踪
y = 2 * x.dot(x)    # 搭建好了computational graph
y.backward()    # backpropagate
print(x.grad)   # 输出梯度
print(x.grad == 4 * x)  # 判断梯度对不对

# 将张量的梯度设置为0用.grad.zero_()。否则会梯度爆炸。而这个梯度清零经常包围在backward()前后，即：
# optimizer.zero_grad()
# loss.backward()   # 这里的loss相当于你的目标函数y = 2 * x.dot(x)
# optimizer.step()
x.grad.zero_()  # 梯度清零
y = x.sum()
y.backward()
print(x.grad)

# 将张量从计算图中分离出来使用.detach()
x.grad.zero_()
y = x * x 
u = y.detach()
z = u * x   

z.sum().backward() # 这里在x的backpropagate，即计算z关于x的偏导数时候，因为.detach()的存在，到u就截止了。
print(x.grad == u)
# --- 这里你一定觉得很奇怪为什么要加sum()，这是因为backward()这个函数只对标量进行计算。当你的计算结果是向量的时候，就得使用sum()或者mean()进行降维，常使用sum().
# 参考链接:https://zhuanlan.zhihu.com/p/427853673

x.5 Probability and Statistics

概率论与数理统计将再开个大的章节进行学习。Maybe 线性代数也是如此。

'''概率论与统计学的知识'''

# 随机变量

# 联合概率

# 条件概率

# 全概率公式

# 贝叶斯公式

# 独立性

# 期望和方差
# --- 在这里我们需要注意的是期望并不等于均值。期望是随变取值乘以随变取值的概率，均值就是随变的平均值。
# --- 为什么我们常常认为期望等于均值呢？是因为我们经常碰到的是高斯分布（正态分布），正态分布的是数学期望等于μ；或者当随便取值等概率的时候，期望也等于均值。

x.6 Pythonic

常见用dir()来查看module中有哪些func, class, attributes等；使用help()来查看API使用方法。查阅文档很有帮助的函数包括如下：

import torch

dir(torch)
help(torch.ones)

'''一些很pythonic的东西'''

# 查看一个module脚本文件有什么函数，类，全局变量等。可以使用dir(file_name) | built-in function

# 查看帮助，一个函数怎么调用等可以使用help(function_name)
# 参考https://zhuanlan.zhihu.com/p/263351646