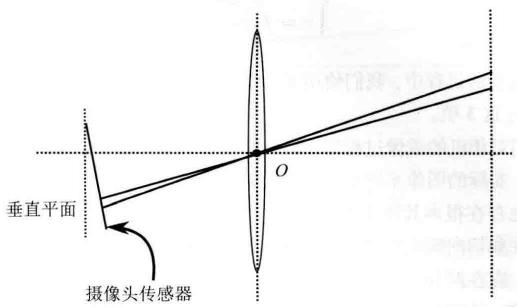
算法背景
经验模态分解(Empirical Mode Decomposition,缩写EMD)是由黄锷(N. E. Huang)在美国国家宇航局与其他人于1998年创造性地提出的一种新型自适应信号时频处理方法,特别适用于非线性非平稳信号的分析处理。
算法过程分析
- 筛选(Sifting)
- 求极值点 通过Find Peaks算法获取信号序列的全部
极大值和极小值- 拟合包络曲线 通过信号序列的
极大值和极小值组,经过三次样条插值法获得两条光滑的波峰/波谷拟合曲线,即信号的上包络线与下包络线- 均值包络线 将两条极值曲线平均获得
平均包络线- 中间信号 原始信号减均值包络线,得到
中间信号- 判断本征模函数(IMF) IMF需要符合两个条件: 1)在整个数据段内,极值点的个数和过零点的个数必须相等或相差最多不能超过一个。 2)在任意时刻,由局部极大值点形成的上包络线和由局部极小值点形成的下包络线的平均值为零,即上、下包络线相对于时间轴局部对称。
- IMF 1 获得的第一个满足IMF条件的中间信号即为原始信号的第一个本征模函数分量
IMF 1(由原数据减去包络平均后的新数据,若还存在负的局部极大值和正的局部极小值,说明这还不是一个本征模函数,需要继续进行“筛选”。)- 使用上述方法得到第一个IMF后,用原始信号减IMF1,作为新的原始信号,再通过上述的筛选分析,可以得到IMF2,以此类推,完成EMD分解。
1. 求极值点
from scipy.signal import argrelextrema
# 通过Scipy的argrelextrema函数获取信号序列的极值点
data = np.random.random(100)
max_peaks = argrelextrema(data, np.greater)
min_peaks = argrelextrema(data, np.less)
# 绘制极值点图像
plt.figure(figsize = (18,6))
plt.plot(data)
plt.scatter(max_peaks, data[max_peaks], c='r', label='Max Peaks')
plt.scatter(min_peaks, data[min_peaks], c='b', label='Max Peaks')
plt.legend()
plt.xlabel('time (s)')
plt.ylabel('Amplitude')
plt.title("Find Peaks") 
2. 拟合包络函数
这一步是EMD的核心步骤,也是分解出本征模函数IMFs的前提。
from scipy.signal import argrelextrema
data = np.random.random(100)-0.5
index = list(range(len(data)))
# 获取极值点
max_peaks = list(argrelextrema(data, np.greater)[0])
min_peaks = list(argrelextrema(data, np.less)[0])
# 将极值点拟合为曲线
ipo3_max = spi.splrep(max_peaks, data[max_peaks],k=3) #样本点导入,生成参数
iy3_max = spi.splev(index, ipo3_max) #根据观测点和样条参数,生成插值
ipo3_min = spi.splrep(min_peaks, data[min_peaks],k=3) #样本点导入,生成参数
iy3_min = spi.splev(index, ipo3_min) #根据观测点和样条参数,生成插值
# 计算平均包络线
iy3_mean = (iy3_max+iy3_min)/2
# 绘制图像
plt.figure(figsize = (18,6))
plt.plot(data, label='Original')
plt.plot(iy3_max, label='Maximun Peaks')
plt.plot(iy3_min, label='Minimun Peaks')
plt.plot(iy3_mean, label='Mean')
plt.legend()
plt.xlabel('time (s)')
plt.ylabel('microvolts (uV)')
plt.title("Cubic Spline Interpolation") 
用原信号减去平均包络线即为所获得的新信号,若新信号中还存在负的局部极大值和正的局部极小值,说明这还不是一个本征模函数,需要继续进行“筛选”。
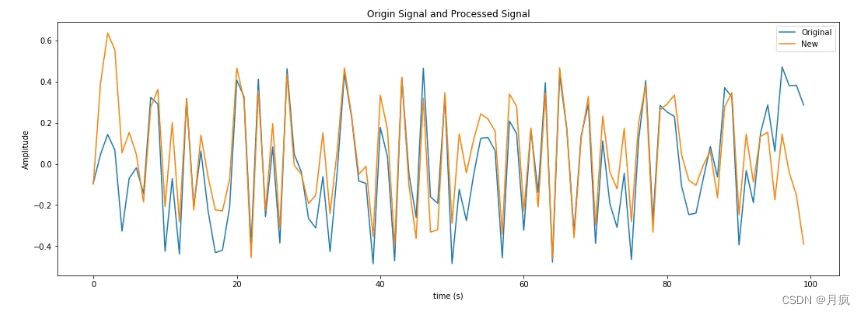
获取本征模函数(IMF)
def sifting(data):
index = list(range(len(data)))
max_peaks = list(argrelextrema(data, np.greater)[0])
min_peaks = list(argrelextrema(data, np.less)[0])
ipo3_max = spi.splrep(max_peaks, data[max_peaks],k=3) #样本点导入,生成参数
iy3_max = spi.splev(index, ipo3_max) #根据观测点和样条参数,生成插值
ipo3_min = spi.splrep(min_peaks, data[min_peaks],k=3) #样本点导入,生成参数
iy3_min = spi.splev(index, ipo3_min) #根据观测点和样条参数,生成插值
iy3_mean = (iy3_max+iy3_min)/2
return data-iy3_mean
def hasPeaks(data):
max_peaks = list(argrelextrema(data, np.greater)[0])
min_peaks = list(argrelextrema(data, np.less)[0])
if len(max_peaks)>3 and len(min_peaks)>3:
return True
else:
return False
# 判断IMFs
def isIMFs(data):
max_peaks = list(argrelextrema(data, np.greater)[0])
min_peaks = list(argrelextrema(data, np.less)[0])
if min(data[max_peaks]) < 0 or max(data[min_peaks])>0:
return False
else:
return True
def getIMFs(data):
while(not isIMFs(data)):
data = sifting(data)
return data
# EMD函数
def EMD(data):
IMFs = []
while hasPeaks(data):
data_imf = getIMFs(data)
data = data-data_imf
IMFs.append(data_imf)
return IMFs
# 绘制对比图
data = np.random.random(1000)-0.5
IMFs = EMD(data)
n = len(IMFs)+1
# 原始信号
plt.figure(figsize = (18,15))
plt.subplot(n, 1, 1)
plt.plot(data, label='Origin')
plt.title("Origin ")
# 若干条IMFs曲线
for i in range(0,len(IMFs)):
plt.subplot(n, 1, i+2)
plt.plot(IMFs[i])
plt.ylabel('Amplitude')
plt.title("IMFs "+str(i+1))
plt.legend()
plt.xlabel('time (s)')
plt.ylabel('Amplitude') 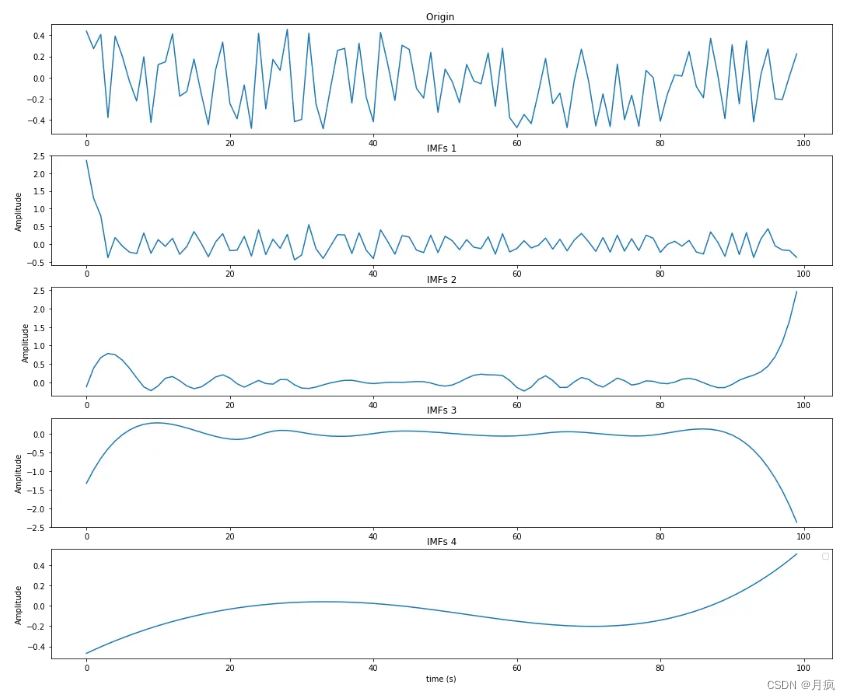
至此就完成了经验模态分解EMD的基本过程。