题目描述
这天,小明在组装齿轮。
他一共有 n 个齿轮,第 i 个齿轮的半径为 ri,他需要把这 n 个齿轮按一定顺序从左到右组装起来,这样最左边的齿轮转起来之后,可以传递到最右边的齿轮,并且这些齿轮能够起到提升或者降低转速 (角速度) 的作用。
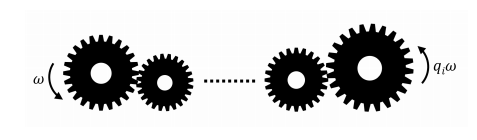
小明看着这些齿轮,突然有 Q 个疑问:能否按一定顺序组装这些齿轮使得最右边的齿轮的转速是最左边的齿轮的 qi 倍?
输入格式
输入共 Q + 2 行,第一行为两个正整数 n, Q,表示齿轮数量和询问数量。
第二行为 n 个正整数 r1,r2, ...,rn,表示每个齿轮的半径。
后面 Q 行,每行一个正整数 qi 表示询问。
输出格式
Q 行,对于每个询问,如果存在至少一种组装方案满足条件,输出 ‘YES‘,否则输出 ‘NO‘。
样例输入
5 3
4 2 3 3 1
2
4
6样例输出
YES
YES
NO提示
询问 1 方案之一:2 3 3 4 1 。
询问 2 方案之一:4 2 3 3 1 。
询问 3 没有方案。
对于 15% 的数据,保证 n, Q ≤ 100 ;
对于 30% 的数据,保证 n, Q ≤ 2000 ;
对于 100% 的数据,保证 n, Q ≤ 2 × 1e5 ; ri , qi ≤ 2 × 1e5 。
解析:
显然,忽略中间的齿轮,问题转换为这个是否存在两个数,他们的比为q。
如果两层遍历找出所有的比值显然超时,所以可以寻找因数,然后记录比值即可。
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int n,q,a[N];
map<int,int>mp;
set<int>s;
int main(){
scanf("%d%d",&n,&q);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
s.insert(a[i]);
}
sort(a+1,a+n+1);
for(int i=1;i<=n;i++){
int t=a[i];
for(int j=1;j*j<=t;j++){
if(t%j==0){
if(s.count(j)) mp[t/j]=1;
if(s.count(t/j)) mp[j]=1;
}
}
}
while(q--){
int t;
scanf("%d",&t);
if(mp.count(t)) puts("YES");
else puts("NO");
}
return 0;
}