1. 前置知识
动态规划与图论,前缀和与差分等有模板的算法不同,动态规划更考察思维能力,而不是运用模板的能力。
个人认为 Acwing 关于动态规划的讲解比较容易理解。我会根据 Acwing 的动态规划解题思路来讲解题目。
虽说动态规划没有固定的模板,但是还是有相对固定的套路。但是思维能力以及经验积累在解决动态规划的题目中十分重要。
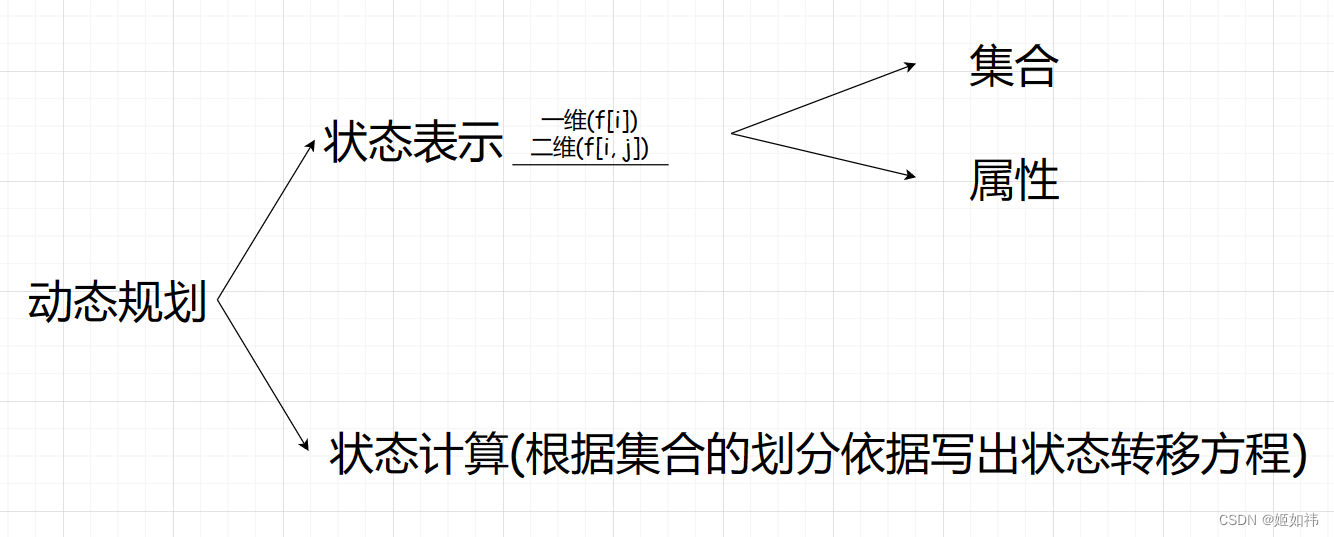
集合:表示状态中每一个下标位置可能的选择。
属性:表示状态中每一个下标位置可能的选择的属性。(一般是最大值或者最小值,将选择附加上属性,就会得到每一个下标位置的最终结果)。
状态计算:将每一个状态中的集合进行划分,根据集合的划分推出状态转移方程。
集合划分的依据:划分出来的所有集合的并集不得遗漏一个状态中的任何选择。但是可以重复。
这些东东可能会很抽象,后面的例题会帮助大家理解这写东东。
2. 01背包问题 (来源:Acwing)
原题链接:2. 01背包问题 - AcWing题库
题目描述:
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。输入格式:
第一行两个整数,N,V,,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi, wi,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式:
输出一个整数,表示最大价值。
数据范围:
0 < N, V ≤1000
0< vi, wi ≤1000输入样例:
4 5 1 2 2 4 3 4 4 5输出样例:
8
我们直接按照上面给出的套路来:
状态表示:f [i, j] (代表状态是一个二维的,这里就不写成二维数组的形式了,比较麻烦。)
二维数组中每一个下标代表的集合:从 1 - i 个物品中选,并且总体积不超过 j 的选法的集合。
属性:集合中选法的最大价值。(将属性附加到集合得到的结果就是二维数组中每个下标的结果)
状态计算:
集合划分:将状态划分成两个集合:1:从1 - i 个物品中选,选择 i ,且价值不超过 j 的所有选法;2:从 1 - (i - 1) 个物品选,不选择 i ,且价值不超过 j 的所有选法。
划分依据的验证:二维数组每一个下标的最终值就是,代表从 1 - i 个物品中选,且总体积不超过 j 的选法的价值最大值。显然这个集合划分没有漏掉该下标位置对应的所有选法。
状态转移方程:根据集合划分,我们只要求出划分出的两个集合中所有选法价值的最大值即可。
注意:j - v[i] 必须保证 j >= v[i] 哦!最终的答案就是 f[N][V] 。
#include<iostream>
using namespace std;
const int N = 1010;
int v[N], w[N];
int f[N][N];
int m, n;
int main()
{
cin >> m >> n;
for(int i = 1; i <= m; i++)
cin >> v[i] >> w[i];
f[0][0] = 0; // 全局变量默认初始化为0,可以不写
for(int i = 1; i <= m; i++)
{
for(int j = 0; j <= n; j++)
{
f[i][j] = f[i - 1][j];
if(j >= v[i])
f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
}
}
cout << f[m][n] << endl;
return 0;
}3. 空间优化
直接将状态从二维压缩到一维,观察结果会不会出错:
f[ i ][ j ] = f[ i - 1][ j ],用到的是上一层即 i - 1 层的状态,若遍历体积大小( j )是从小到大遍历,那么状态压缩之后的计算结果就是用第 i 层的状态来算的,不正确,因此我们需要改变遍历的顺序,从大到小遍历。
f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]),用到的同样是上一层的状态,因此同样不能从小到达遍历体积,必须从大到小遍历体积才能保证状态的转移是从上一层来的。
综上所述,只需要改变体积的遍历顺序就可以将二维的状态压缩到一维。
#include<iostream>
using namespace std;
const int N = 1010;
int v[N], w[N];
int f[N];
int m, n;
int main()
{
cin >> m >> n;
for(int i = 1; i <= m; i++)
cin >> v[i] >> w[i];
f[0] = 0; // 全局变量默认初始化为0,可以不写
for(int i = 1; i <= m; i++)
for(int j = n; j - v[i] >= 0; j--)
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[n] << endl;
return 0;
}