目录
一、什么是小数
二、浮点数在计算机中的转换规则
（1）整数部分转换步骤
（2） 小数部分转换步骤
三、使用代码说明
四、手动转换小数
一、什么是小数
在计算机中，也称小数为浮点数，因为在使用科学计数法时，数字的小数点是可以“浮动”的。
在Java中，关于浮点数有两种数据类型：
| Float | Double | |
| 含义 | 单精度浮点数 | 双精度浮点数 |
| Java中的默认值 | 不是默认浮点数类型 | 是默认浮点数类型 |
| Java中所占字节数 | 4字节 | 8字节 |
| 最大值 | 3.4E38 | 1.79E308 |
二、浮点数在计算机中的转换规则
数字在计算机中是采用二进制存储的，在将小数存入计算机中时，要将十进制转为二进制，最后呈现给我们的是二进制在重新转换为十进制的结果。而在十进制转换为二进制的过程中，极易出现无限循环的情况，因此小数将变得不再精确。计算机最终会取一个无限接近结果的小数作为结果。
十进制数转换为二进制数时，需要对整数部分与小数部分分别进行转换。
（1）整数部分转换步骤
1.使用十进制的值除以2，得到两个部分，商和余数；
2.商继续除以2，直到商为0为止；
3.余数倒着看，就是二进制的值。
（2） 小数部分转换步骤
1.整数部分转整数部分，小数部分转小数部分；
2.把十进制的小数乘以2：
(1).结果如果大于1，转换后的小数后面记1；
(2).结果如果小于1，转换后的小数后面记0。
3.直到结果为1.0为止。
三、使用代码说明
public class Demo01 {
public static void main(String[] args) {
double x = 10 - 9.9;
double y = 1.0 - 9.0 / 10;
//观察x和y是否相等：
System.out.println(x);
System.out.println(y);
//判断x和y是否相等
System.out.println(x == y);
System.out.println(Math.abs(x - y) < 0.000001); //Math.abs()取绝对值
}
}运行结果：
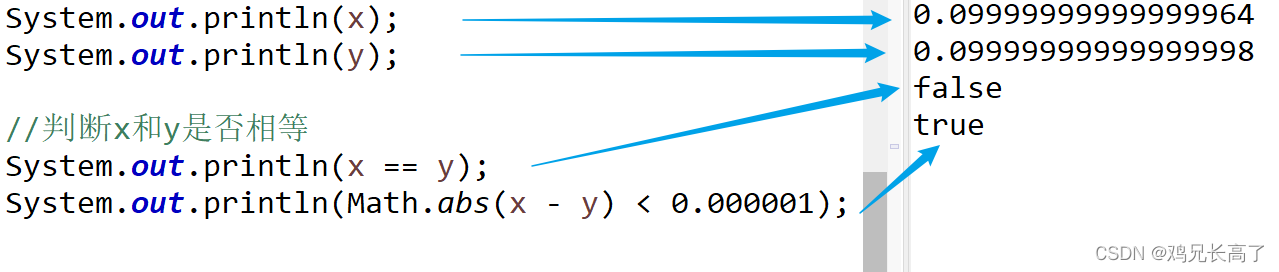
我们发现，在日常计算中，x与y的值应该是相等的，但是使用浮点数进行除法运算后，就已经将值变得不精确了，因此，两个算式的最终结果不一致，并且相差很小。
四、手动转换小数
将十进制数0.6转换为二进制数
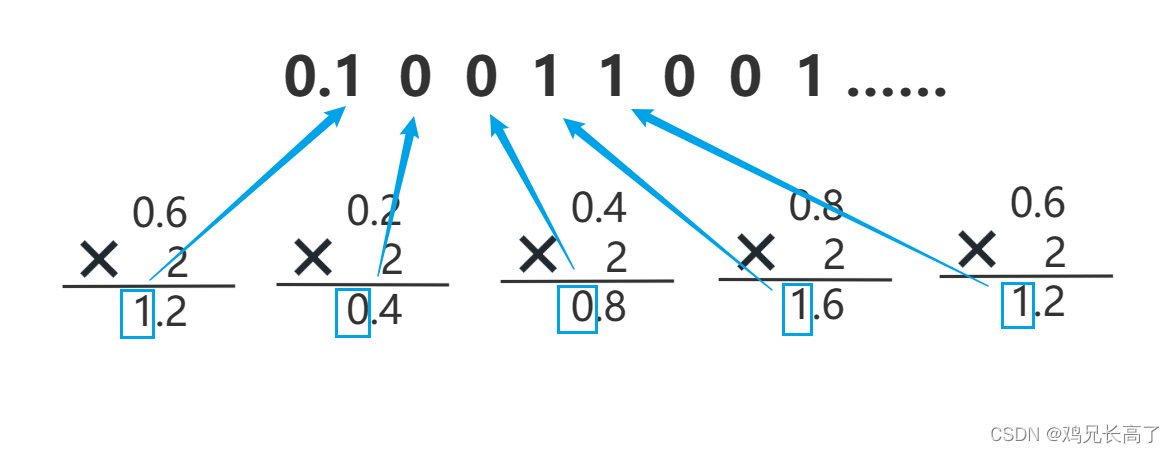我们发现，这里出现了循环，因此浮点数是不精确的。
