💗 💗 博客:小怡同学
💗 💗 个人简介:编程小萌新
💗 💗 如果博客对大家有用的话,请点赞关注再收藏 🌞
快速排序
快速排序是任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止
方法一
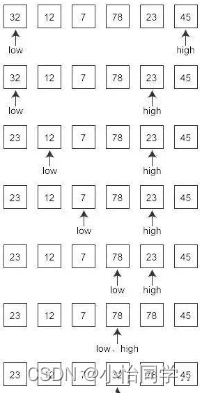
//代码实现
void QuickSort(int* a, int left, int right)
{
if (left >= right)
{
return;
}
int end = right;
int begin = left;
int key = left;
while (left < right)
{
while (left < right && a[key] <= a[right])
{
right--;
}
while (left < right && a[key] >= a[left])
{
left++;
}
swap(&a[right], &a[left]);
}
swap(&a[key], &a[left]);
PartSort1(a, begin, left - 1);
PartSort1(a, left + 1, end);
}
//key的下标与开始遍历的方向是反方向 ,如果在同一方向 则会交换错误
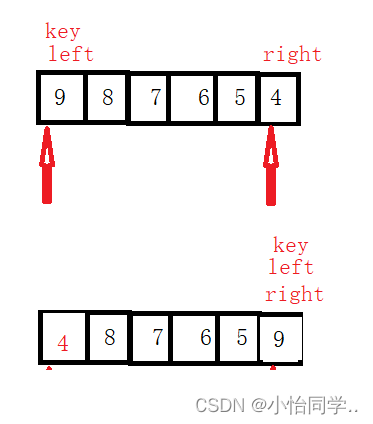
//交换条件是left < right &&left <= right
1是保证在正确交换
2是left必须<= right
因为不带等号会陷入死循环
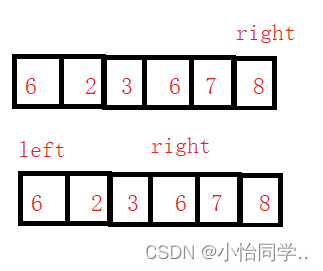
递归结束条件是 left >= right
方法二(挖坑法)
void QucikSort(int* a, int left, int right)
{
if (left >= right)
{
return;
}
int key = a[left];
int begin = left;
int end = right;
int hole = left;
while (left <right)
{
while (left < right && a[right] >= key)
{
right--;
}
swap(&a[right], &a[hole]);
hole = right;
while (left < right && a[left] <= key)
{
left++;
}
swap(&a[left],&a[hole]);
hole = left;
}
a[hole] = key;
PartSort2(a, begin, hole - 1);
PartSort2(a, hole + 1, end);
}
方法三(前后指针法)
void QuickSort(int* a, int left, int right)
{
if (left >= right)
{
return;
}
int prev = left;
int end = left+1;
int key = left;
while (end <= right )
{
if (a[end] < a[key] && ++prev != end)
{
swap(&a[prev], &a[end]);
}
end++;
}
swap(&a[key], &a[prev]);
PartSort3(a, left, prev - 1);
PartSort3(a, prev + 1, right);
}
方法四(非递归法)
void QuickSort(int* a, int left, int right)
{
Stack pq;
StackInit(&pq);
StackPush(&pq, right);
StackPush(&pq, left);
while (!StackEmpty(&pq))
{
int begin = StackTop(&pq);
StackPop(&pq);
int end = StackTop(&pq);
StackPop(&pq);
int key = QuickSort1(a, begin, end);
if (key < right -1)
{
StackPush(&pq, right);
StackPush(&pq, key+1);
}
if(begin < key-1)
{
StackPush(&pq, key-1);
StackPush(&pq, begin);
}
}
StackDestory(&pq);
}
性能优化
当顺序与目标顺序是相反时,时间复杂度为o(N^2)
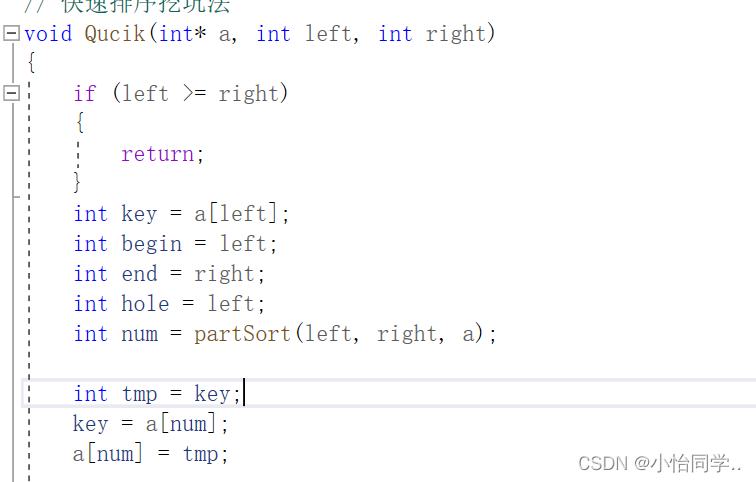
最后几次层栈的调用占据了调用的一大半,所以将最后几层优化
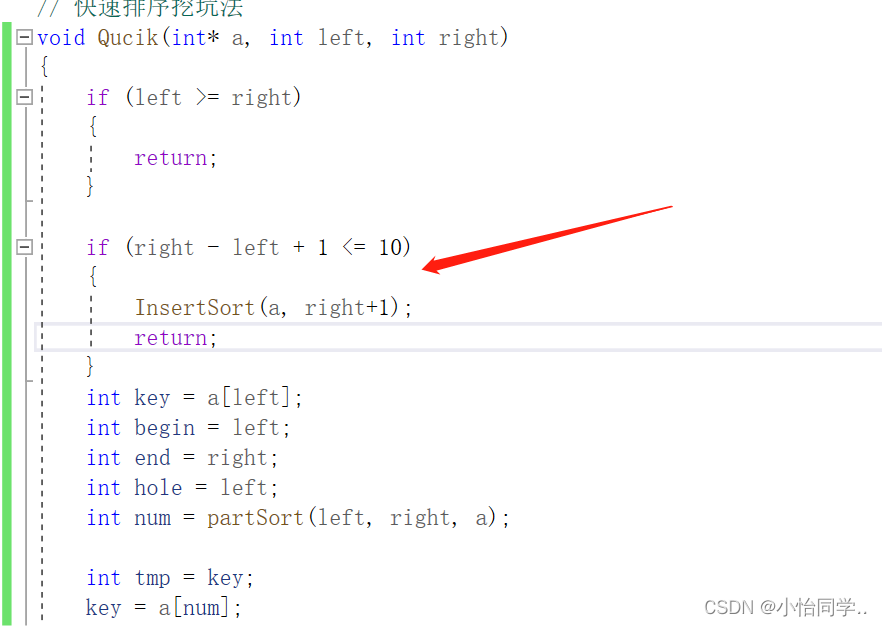
时间复杂度和稳定性
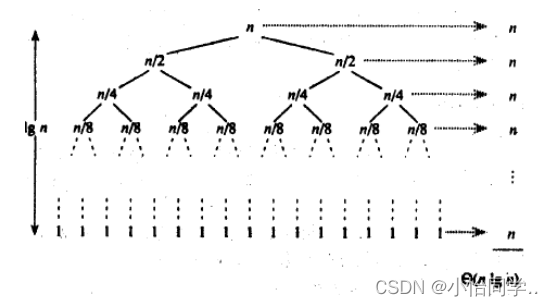
稳定性:不稳定
时间复杂度:NlogN
//共logN层
//n + (n-1) + (n-3) + …约等于NlogN