糖酵解反应动力学方程的微分方程建模

题目

对于下面的糖酵解反应：

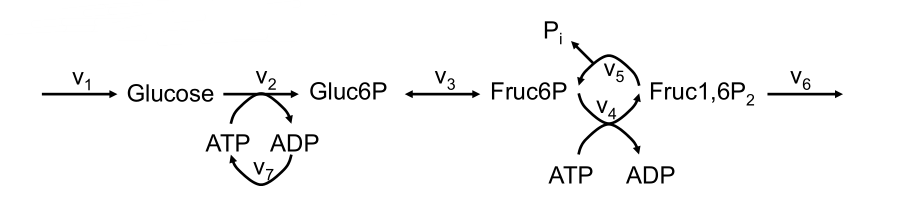
设其满足如下动力学方程：
$$\{\begin{array}{l}\frac{d}{dt}\text{ Glucose }=v_1-v_2\\ \frac{d}{dt}\text{ Gluc }6P=v_2-v_3\\ \frac{d}{dt}\text{ Fruc }6P=v_3-v_4+v_5\\ \frac{d}{dt}\text{ Fruc }1,6P_2=v_4-v_5-v_6\\ \frac{d}{dt}\text{ ATP }=-\frac{d}{dt}\text{ ADP }=-v_2-v_4+v_7\end{array}\{\begin{array}{l}{v}_1=\text{ constant }=k_1\\ v_2=k_2\cdot \text{ Glucose }\cdot \text{ ATP }\\ v_3=k_3\cdot \text{ Gluc }6P-k_{-3}\cdot \text{ Fruc }6P\\ v_4=k_4\cdot \text{ Fruc }6P\cdot ATP\\ v_5=k_5\cdot \text{ Fruc }1,6P_2\\ v_6=k_6\cdot \text{ Fruc }1,6P_2\\ v_7=k_7\cdot ADP\end{array}$$

$$\text{ 令, }{k}_1=0.25,k_2=1,k_3=1,k_{-3}=1,k_4=1,k_5=1,k_6=1,k_7=2.5$$
设 $t=0$ 时的初始浓度为:
$$\mathrm{Glucose}(0)=\mathrm{Gluc}6P(0)=\mathrm{Fruc}6P(0)=F_{ruc1},6P_2(0)=0,ATP(0)=ADP(0)=0.5\text{ (任意单位) }$$
试用MatLab软件求解并画出6种物质的时间过程曲线, 并选取适当的时间区间, 在二 维相平面中, 以Glucose的浓度值为横轴, 以$Fruc1,6P_2$ 的浓度值为纵轴, 画两种物质浓度之间的关系曲线 (轨迹)。
要求: 给出可执行代码, 并写出运行步骤, 保证可以按照操作步骤, 得到所需的结果。

解答

引言

糖酵解是一种重要的生化通路，它将葡萄糖转化为能量。研究糖酵解反应的动力学方程可以帮助我们了解这一过程中各物质浓度的变化规律。我将介绍糖酵解反应的动力学方程，并使用MatLab软件求解和可视化该方程的数值解。

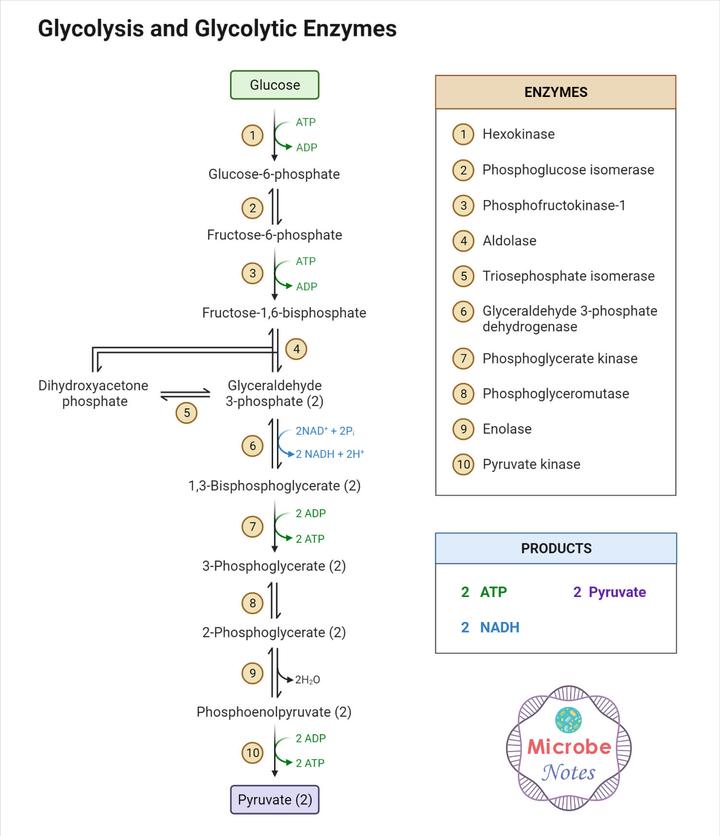
糖酵解反应动力学方程

糖酵解反应涉及多个物质之间的相互转化，其中包括葡萄糖（Glucose）、葡萄糖-6-磷酸（Gluc6P）、果糖-6-磷酸（Fruc6P）、果糖-1,6-二磷酸（Fruc1,6P2）、三磷酸腺苷（ATP）和三磷酸腺苷二磷酸（ADP）。这些物质之间的转化关系可以用一组微分方程来描述。

我们将使用下面的动力学方程来模拟糖酵解反应：

$$\begin{array}{rl}\frac{d}{dt}\text{Glucose}& =v_1-v_2\\ \frac{d}{dt}\text{Gluc}6P& =v_2-v_3\\ \frac{d}{dt}\text{Fruc}6P& =v_3-v_4+v_5\\ \frac{d}{dt}\text{Fruc}1,6P2& =v_4-v_5-v_6\\ \frac{d}{dt}\text{ATP}& =-\frac{d}{dt}\text{ADP}=-v_2-v_4+v_7\end{array}$$

其中，$v_1,v_2,v_3,v_4,v_5,v_6,v_7$是给定的常数，它们代表了不同反应的速率。

使用MatLab求解动力学方程

MatLab是一种强大的数值计算软件，可以用于求解微分方程。在这里，我们将使用MatLab中的ode45函数来求解糖酵解反应的动力学方程。

首先，我们需要定义一个函数来表示方程组的右侧，即微分方程的等式右边。在MatLab中，可以使用函数句柄来定义这个函数。下面是我们定义方程组的代码：

% 定义初始条件向量
y0 = [Glucose; Gluc6P; Fruc6P; Fruc1_6P2; ATP; ADP];

% 定义方程组，y(n)表示着y0的第n个物质
dydt = @(t, y) [
    k1 - k2 * y(1) * y(5);
    k2 * y(1) * y(5) - k3 * y(2) + k_minus3 * y(3);
    k3 * y(2) - k_minus3 * y(3) - k4 * y(3) * y(5) + k5 * y(4);
    k4 * y(3) * y(5) - k5 * y(4) - k6 * y(4);
    -k2 * y(1) * y(5) - k4 * y(3) * y(5) + k7 * y(6);
    k2 * y(1) * y(5) + k4 * y(3) * y(5) - k7 * y(6)
];

在这个代码中，dydt是一个函数句柄，它接受两个参数t和y，分别代表时间和状态变量。函数体部分是一个矩阵，其中每一行对应方程组的一个微分方程。矩阵中的每个元素都是根据给定的常数和变量进行计算的。

接下来，我们需要指定初始条件和时间范围。根据题目给出的条件，我们可以将初始条件设置如下：

% 定义初始浓度
Glucose = 0;
Gluc6P = 0;
Fruc6P = 0;
Fruc1_6P2 = 0;
ATP = 0.5;
ADP = 0.5;

% 定义时间区间
tspan = [0 10]; % 这里选择了0到10的时间区间

% 定义初始条件向量
y0 = [Glucose; Gluc6P; Fruc6P; Fruc1_6P2; ATP; ADP];

最后，我们可以使用ode45函数来求解微分方程组，并得到数值解：

% 求解方程组
[t, y] = ode45(dydt, tspan, y0);

在这个代码中，ode45函数接受三个参数：函数句柄dydt、时间范围tspan和初始条件y0。它返回两个变量t和y，分别代表求解得到的时间和状态变量的数值解。

结果可视化

最后，我们可以使用MatLab的绘图功能将糖酵解反应的各物质浓度随时间的变化绘制出来。

% 绘制时间过程曲线
figure;
plot(t, Glucose, 'r', t, y(:, 2), 'g', t, y(:, 3), 'b', t, Fruc1_6P2, 'm', t, y(:, 5), 'c', t, y(:, 6), 'y');
legend('Glucose', 'Gluc6P', 'Fruc6P', 'Fruc1,6P2', 'ATP', 'ADP');
xlabel('Time');
ylabel('Concentration');
title('Time Profiles of Substances');

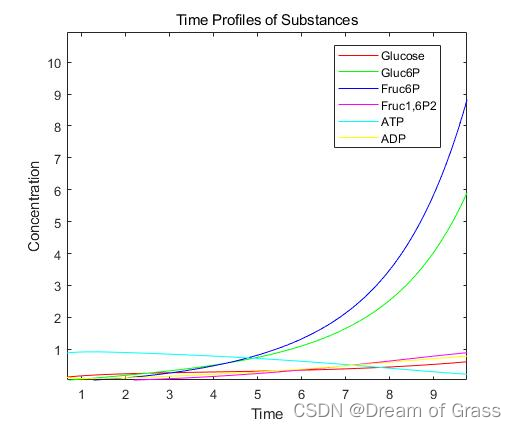
下面绘制Glucose和Fruc1,6P2之间关系曲线：

% 绘制时间过程曲线
figure;
plot(t, Glucose, 'r', t, y(:, 2), 'g', t, y(:, 3), 'b', t, Fruc1_6P2, 'm', t, y(:, 5), 'c', t, y(:, 6), 'y');
legend('Glucose', 'Gluc6P', 'Fruc6P', 'Fruc1,6P2', 'ATP', 'ADP');
xlabel('Time');
ylabel('Concentration');
title('Time Profiles of Substances');

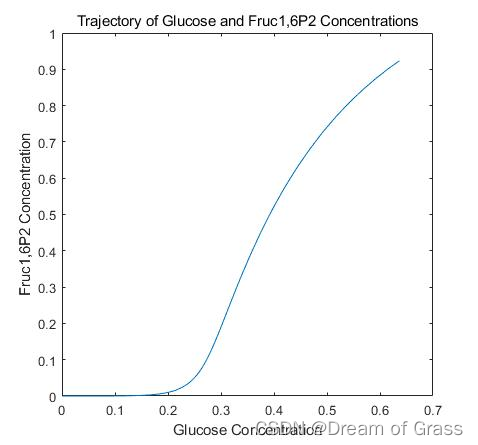
结论

本文介绍了糖酵解反应动力学方程的数值求解方法。通过使用MatLab软件和ode45函数，我们可以得到糖酵解反应中各物质浓度随时间的变化。通过绘制曲线，我们可以直观地了解糖酵解反应的动力学特性。

完整代码

% 定义常数
k1 = 0.25;
k2 = 1;
k3 = 1;
k_minus3 = 1;
k4 = 1;
k5 = 1;
k6 = 1;
k7 = 2.5;

% 定义初始浓度
Glucose = 0;
Gluc6P = 0;
Fruc6P = 0;
Fruc1_6P2 = 0;
ATP = 0.5;
ADP = 0.5;

% 定义时间区间
tspan = [0 10]; % 这里选择了0到10的时间区间

% 定义初始条件向量
y0 = [Glucose; Gluc6P; Fruc6P; Fruc1_6P2; ATP; ADP];

% 定义方程组，y(n)表示着y0的第n个物质
dydt = @(t, y) [
    k1 - k2 * y(1) * y(5);
    k2 * y(1) * y(5) - k3 * y(2) + k_minus3 * y(3);
    k3 * y(2) - k_minus3 * y(3) - k4 * y(3) * y(5) + k5 * y(4);
    k4 * y(3) * y(5) - k5 * y(4) - k6 * y(4);
    -k2 * y(1) * y(5) - k4 * y(3) * y(5) + k7 * y(6);
    k2 * y(1) * y(5) + k4 * y(3) * y(5) - k7 * y(6)
];

% 求解方程组
[t, y] = ode45(dydt, tspan, y0);

% 提取各物质浓度
Glucose = y(:, 1);
Fruc1_6P2 = y(:, 4);

% 绘制时间过程曲线
figure;
plot(t, Glucose, 'r', t, y(:, 2), 'g', t, y(:, 3), 'b', t, Fruc1_6P2, 'm', t, y(:, 5), 'c', t, y(:, 6), 'y');
legend('Glucose', 'Gluc6P', 'Fruc6P', 'Fruc1,6P2', 'ATP', 'ADP');
xlabel('Time');
ylabel('Concentration');
title('Time Profiles of Substances');
% 绘制Glucose和Fruc1,6P2之间的关系曲线（轨迹）
figure;
plot(Glucose, Fruc1_6P2);
xlabel('Glucose Concentration');
ylabel('Fruc1,6P2 Concentration');
title('Trajectory of Glucose and Fruc1,6P2 Concentrations');