算法修炼之筑基篇——筑基二层初期（解决最长回文子串问题，马拉车(manacher)算法模板）

news2024/11/25 2:48:00

✨博主：命运之光

🦄专栏：算法修炼之练气篇

🍓专栏：算法修炼之筑基篇

✨博主的其他文章：点击进入博主的主页

前言：学习了算法修炼之练气篇想必各位蒟蒻们的基础已经非常的扎实了，下来我们进阶到算法修炼之筑基篇的学习。筑基期和练气期难度可谓是天差地别，懂得都懂，题目难度相比起练气期的题目难度提升很多，所以要是各位蒟蒻小伙伴们看不懂筑基期的题目可以在练气期多积累积累，练气期的题目也会不断更新，大家一定要把基础打牢固了再来看筑基期的题目哈，这样子也可以提高大家的学习效率，一举两得，加油(●'◡'●)🎉🎉

目录

✨如何解决最长回文子串这类问题

✨最长回文子串（例题🦄）

🍓我们先用中心扩展法来写这道问题

🍓我们修改代码采用马拉车算法（Manacher's algorithm）来解决：

✨马拉车算法的标准模板

✨模板使用讲解+使用

✨结语

✨如何解决最长回文子串这类问题

常见方法包括暴力法、动态规划和马拉车算法。下面我将简要介绍这些方法：

  1. 暴力法： 暴力法是最简单直接的方法，即对于给定字符串的每个可能的子串，判断是否是回文串并记录最长的回文串。这种方法的时间复杂度为 O(n^3)，其中 n 是字符串的长度。尽管暴力法的效率较低，但对于较小的输入规模，它是可行的。
  2. 动态规划： 动态规划方法可以通过构建状态转移方程来解决最长回文子串问题。定义一个二维数组 dp，其中 dp[i][j] 表示从下标 i 到下标 j 的子串是否是回文串。根据回文串的性质，有以下状态转移方程：
dp[i][j] = true, if i == j    （单个字符是回文串）
dp[i][j] = (s[i] == s[j]), if j - i == 1   （相邻字符相等时是回文串）
dp[i][j] = (s[i] == s[j] && dp[i+1][j-1]), if j - i > 1   （首尾字符相等且内部子串是回文串时是回文串）

通过填充动态规划表格 dp，可以找到最长回文子串的长度和起始位置。该方法的时间复杂度为 O(n^2)。

        3.马拉车算法（Manacher's algorithm）： 马拉车算法是一种高效的线性时间算法，用于找到最长回文子串。该算法通过利用回文串的对称性进行优化，避免了重复计算。马拉车算法的核心思想是利用一个数组 P 来记录以每个字符为中心的回文串半径长度（不包括中心字符）。通过维护一个当前已知回文串的中心和右边界，算法在线性时间内找到所有位置的最长回文串半径。通过预处理字符串，将其转换为更易处理的形式，然后应用马拉车算法，可以找到最长回文子串的长度和起始位置。马拉车算法的时间复杂度为 O(n)。

这些方法各有优劣，选择合适的方法取决于问题的规模和时间要求。对于较小的输入规模，可以使用暴力法或动态规划。对于较大的输入规模，马拉车算法是更高效的选择。

✨最长回文子串（例题🦄）

🍓我们先用中心扩展法来写这道问题

中心扩展法是一种简单直观的方法，用于寻找最长回文子串。它的基本思想是遍历字符串中的每个字符，将当前字符作为中心，同时考虑奇数长度和偶数长度的回文子串，通过不断向两边扩展并比较字符，找到以当前字符为中心的最长回文子串的长度。

中心扩展法的步骤如下：

  1. 遍历字符串中的每个字符，将其依次作为回文串的中心。
  2. 对于每个中心字符，分别向左右两边扩展，直到无法扩展或左右字符不相等为止。
  3. 记录每个中心字符的回文串长度，并更新最长回文串的长度和起始位置。

中心扩展法的时间复杂度为 O(n^2)，其中 n 是字符串的长度。对于较小的输入规模，中心扩展法是一个简单易懂的选择。

它是解决最长回文子串问题的一个基本方法，易于理解和实现。虽然中心扩展法的时间复杂度较高，但对于规模较小的问题或者作为一种简单的初始方法，它是一个合理的选择。

#include <iostream>
#include <vector>

using namespace std;

// 中心扩展法
int expandAroundCenter(string s, int left, int right) {
    while (left >= 0 && right < s.length() && s[left] == s[right]) {
        left--;
        right++;
    }
    return right - left - 1;
}

string longestPalindrome(string s) {
    int start = 0, end = 0;

    for (int i = 0; i < s.length(); i++) {
        int len1 = expandAroundCenter(s, i, i);
        int len2 = expandAroundCenter(s, i, i + 1);
        int len = max(len1, len2);

        if (len > end - start) {
            start = i - (len - 1) / 2;
            end = i + len / 2;
        }
    }

    return s.substr(start, end - start + 1);
}

int main() {
    string s;
    cin >> s;

    string longest = longestPalindrome(s);
    cout << longest.length() << endl;

    return 0;
}

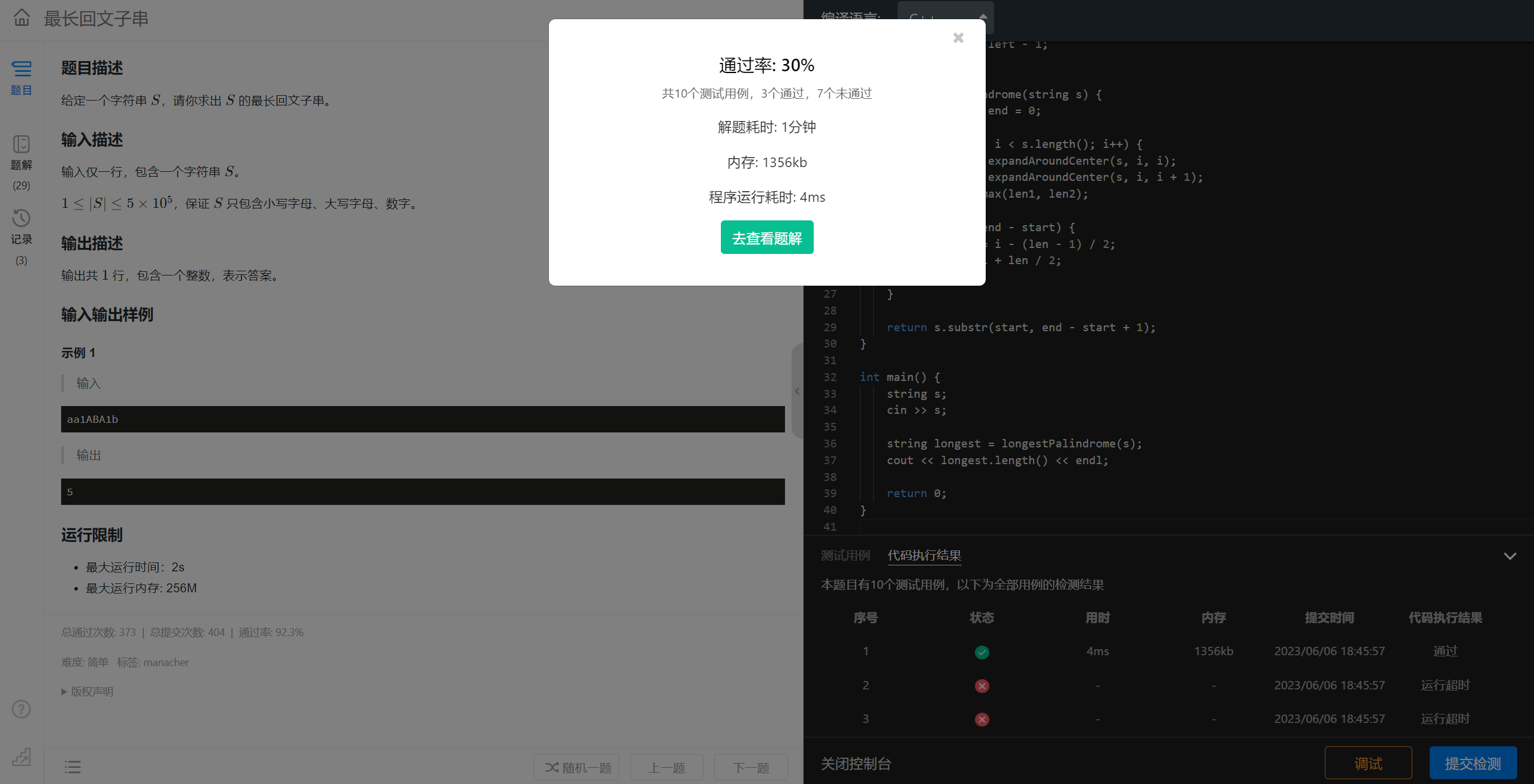
显然问题规模太大中心扩展法的时间复杂度爆掉了

🍓我们修改代码采用马拉车算法（Manacher's algorithm）来解决：

#include <iostream>
#include <vector>

using namespace std;

string preProcess(string s) {
    int n = s.length();
    if (n == 0) {
        return "^$";
    }

    string processed = "^";
    for (int i = 0; i < n; i++) {
        processed += "#" + s.substr(i, 1);
    }
    processed += "#$";

    return processed;
}

string longestPalindrome(string s) {
    string processed = preProcess(s);
    int n = processed.length();

    vector<int> P(n, 0);
    int center = 0, right = 0;

    for (int i = 1; i < n - 1; i++) {
        int i_mirror = 2 * center - i;

        if (right > i) {
            P[i] = min(right - i, P[i_mirror]);
        }

        while (processed[i + 1 + P[i]] == processed[i - 1 - P[i]]) {
            P[i]++;
        }

        if (i + P[i] > right) {
            center = i;
            right = i + P[i];
        }
    }

    int maxLen = 0, centerIndex = 0;
    for (int i = 1; i < n - 1; i++) {
        if (P[i] > maxLen) {
            maxLen = P[i];
            centerIndex = i;
        }
    }

    int start = (centerIndex - maxLen) / 2;
    return s.substr(start, maxLen);
}

int main() {
    string s;
    cin >> s;

    string longest = longestPalindrome(s);
    cout << longest.length() << endl;

    return 0;
}

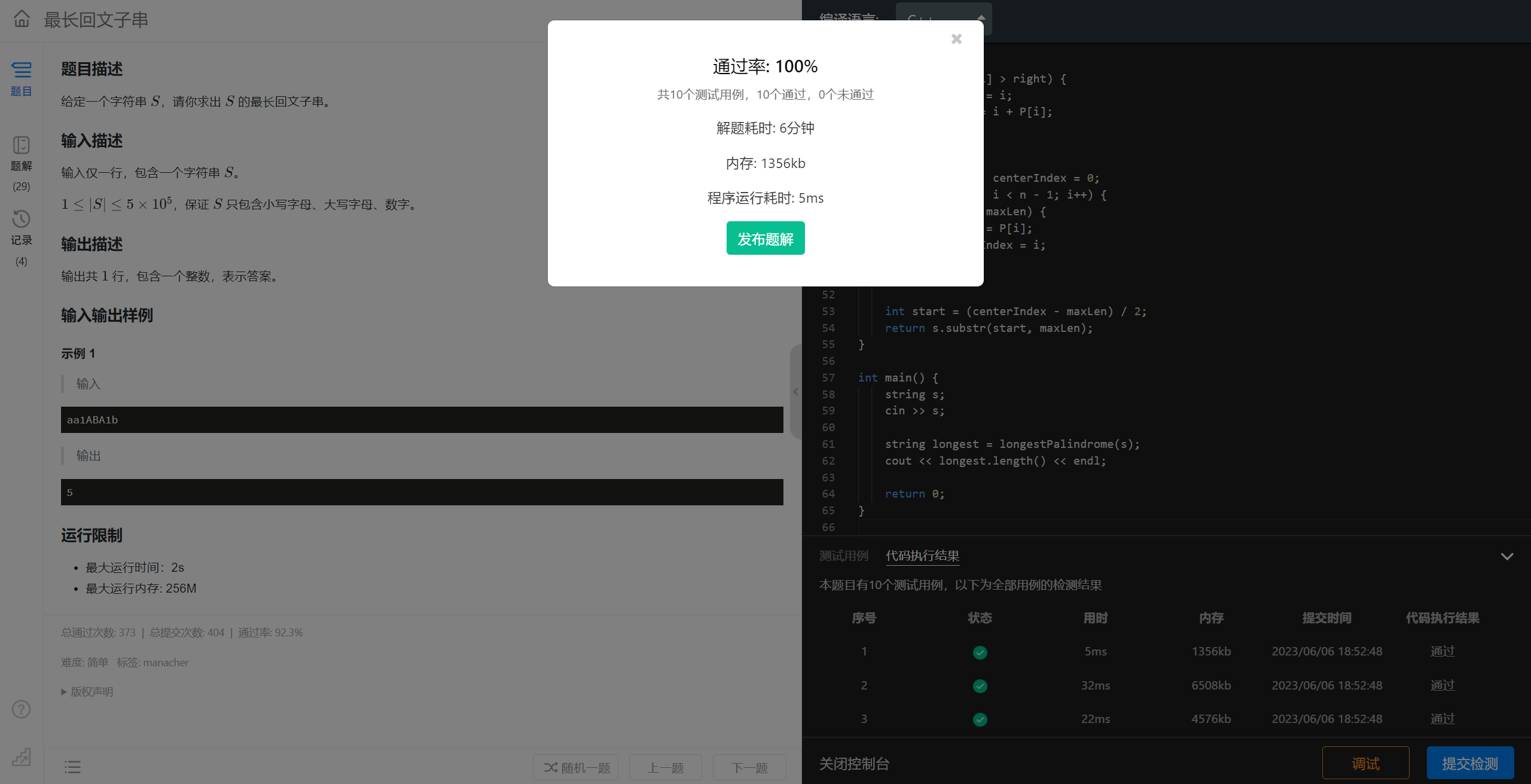
🎉🎉🎉成功通过🎉🎉🎉

🍓下来我们详细解释以下上述马拉车算法让没学过马拉车算法的小白也能听的懂

#include <iostream>
#include <vector>

using namespace std;
这部分是引入需要的头文件和命名空间。

string preProcess(string s) {
    int n = s.length();
    if (n == 0) {
        return "^$";
    }

    string processed = "^";
    for (int i = 0; i < n; i++) {
        processed += "#" + s.substr(i, 1);
    }
    processed += "#$";

    return processed;
}

这是一个预处理函数 preProcess，它将原始字符串进行处理，以便进行马拉车算法。该函数在每个字符的左右两侧添加特殊字符（通常为不在原始字符串中出现的字符）以构建预处理字符串。

string longestPalindrome(string s) {
    string processed = preProcess(s);
    int n = processed.length();

    vector<int> P(n, 0);
    int center = 0, right = 0;

    for (int i = 1; i < n - 1; i++) {
        int i_mirror = 2 * center - i;

        if (right > i) {
            P[i] = min(right - i, P[i_mirror]);
        }

        while (processed[i + 1 + P[i]] == processed[i - 1 - P[i]]) {
            P[i]++;
        }

        if (i + P[i] > right) {
            center = i;
            right = i + P[i];
        }
    }

    int maxLen = 0, centerIndex = 0;
    for (int i = 1; i < n - 1; i++) {
        if (P[i] > maxLen) {
            maxLen = P[i];
            centerIndex = i;
        }
    }

    int start = (centerIndex - maxLen) / 2;
    return s.substr(start, maxLen);
}

这是主要的函数 longestPalindrome，它使用马拉车算法找到最长回文子串。首先，我们调用 preProcess 函数对输入字符串进行预处理，得到预处理字符串 processed 和其长度 n。

我们创建了一个大小为 n 的数组 P，用于记录以每个字符为中心的回文串的半径长度（不包括中心字符）。同时，我们初始化两个变量 center 和 right，分别表示已知的回文串的中心和右边界。

接下来，我们从下标为 1 的字符开始遍历预处理字符串，依次计算 P 数组的值。首先，我们根据当前字符的对称性，找到它关于中心的镜像下标 i_mirror。如果当前字符在已知回文串的右边界内，我们可以利用回文串的对称性来快速计算 P[i] 的值。如果超出右边界，则以当前字符为中心，向两边扩展并比较字符，更新 P[i] 的值。

接下来，我们通过不断扩展和比较字符的循环，计算每个中心字符的回文串半径长度，并更新已知的回文串中心和右边界。

完成循环后，我们找到 P 数组中最大值，确定最长回文子串的长度 maxLen 和中心位置的下标 centerIndex。

最后，我们通过计算起始位置 start，从原始字符串 s 中提取出最长回文子串，并将其作为函数的返回值。

int main() {
    string s;
    cin >> s;

    string longest = longestPalindrome(s);
    cout << longest.length() << endl;

    return 0;
}

在 main 函数中，我们读取输入字符串 s，调用 longestPalindrome 函数找到最长回文子串，并输出其长度。

这样，通过马拉车算法的实现，我们可以找到给定字符串的最长回文子串。

上面给出的马拉车算法代码可以作为一个模板，用于解决求最长回文子串的问题。只要将输入的字符串传递给 longestPalindrome 函数，就可以得到最长回文子串的长度和具体子串。

当你遇到求最长回文子串的问题时，可以使用这个模板作为起点，进行适当的修改和调整来满足具体的问题要求。

例如，如果你需要返回最长回文子串的具体位置或者需要统计所有的最长回文子串，你可以对模板代码进行扩展。你可能需要记录每个回文子串的起始位置和长度，并在遍历过程中更新这些信息。

根据具体问题的要求，你还可以对代码进行优化和改进。马拉车算法有许多变种和优化技巧，如使用 manacher 数组来减少计算量，提前终止循环等。

记住马拉车算法是解决最长回文子串问题的高效算法，可以作为一个有用的模板来解决类似的问题，但你可能需要根据具体情况进行适当的修改和扩展。

✨马拉车算法的标准模板

#include <iostream>
#include <vector>

using namespace std;

string longestPalindrome(string s) {
    string processed = "#";
    for (int i = 0; i < s.length(); i++) {
        processed += s[i];
        processed += "#";
    }

    int n = processed.length();
    vector<int> P(n, 0);
    int center = 0, right = 0;

    for (int i = 1; i < n - 1; i++) {
        int i_mirror = 2 * center - i;

        if (right > i) {
            P[i] = min(right - i, P[i_mirror]);
        }

        while (processed[i + 1 + P[i]] == processed[i - 1 - P[i]]) {
            P[i]++;
        }

        if (i + P[i] > right) {
            center = i;
            right = i + P[i];
        }
    }

    int maxLen = 0, centerIndex = 0;
    for (int i = 1; i < n - 1; i++) {
        if (P[i] > maxLen) {
            maxLen = P[i];
            centerIndex = i;
        }
    }

    int start = (centerIndex - maxLen) / 2;
    return s.substr(start, maxLen);
}

int main() {
    string s;
    cin >> s;

    string longest = longestPalindrome(s);
    cout << longest << endl;

    return 0;
}

这个模板包含了马拉车算法的核心部分，可以直接用于求解最长回文子串问题。

你只需将输入的字符串传递给 longestPalindrome 函数，即可得到最长回文子串。注意，此模板假设输入字符串只包含小写字母、大写字母和数字。

你可以根据需要，自行扩展和修改模板代码，例如记录回文子串的位置、统计所有最长回文子串等。另外，为了适应不同的比赛环境，你可能需要添加适当的输入输出代码。

✨模板使用讲解+使用

🦄相信肯定有许多小伙伴看不懂模板，也不会用模板，没关系，下来详细的讲解一下模板，和模板的使用。

string longestPalindrome(string s) {
    string processed = "#";
    for (int i = 0; i < s.length(); i++) {
        processed += s[i];
        processed += "#";
    }

这部分代码定义了 longestPalindrome 函数，它接收一个字符串 s 作为参数，并返回最长回文子串。

首先，我们创建了一个新的字符串 processed，并在其开头插入一个特殊字符 #。接下来，我们遍历输入字符串 s 中的每个字符，将其插入 processed 中，并在字符之间插入特殊字符 #。这样做是为了将原始字符串的每个字符作为回文串的中心字符，以便更方便地处理回文串的奇偶长度情况。

  int n = processed.length();
    vector<int> P(n, 0);
    int center = 0, right = 0;

    for (int i = 1; i < n - 1; i++) {
        int i_mirror = 2 * center - i;

        if (right > i) {
            P[i] = min(right - i, P[i_mirror]);
        }

        while (processed[i + 1 + P[i]] == processed[i - 1 - P[i]]) {
            P[i]++;
        }

        if (i + P[i] > right) {
            center = i;
            right = i + P[i];
        }
    }

在这一部分中，我们执行马拉车算法的核心部分。我们首先创建一个大小为 n 的数组 P，用于记录以每个字符为中心的回文串的半径长度。

然后，我们初始化两个变量 center 和 right，表示当前已知的回文串的中心和右边界。在循环中，我们从下标为 1 的字符开始遍历 processed 字符串。

对于每个下标 i，我们计算其关于中心的镜像下标 i_mirror。接下来，我们根据已知回文串的右边界来计算 P[i] 的初始值。如果 right 大于 i，我们可以利用回文串的对称性来快速计算 P[i]。具体来说，P[i] 取 right - i 和 P[i_mirror] 中的较小值。

然后，我们通过扩展和比较字符的循环，来计算每个中心字符的回文串半径长度。我们不断地将 i 扩展到左右字符相等的位置，并更新 P[i] 的值。这一过程结束后，我们可能会更新已知回文串的中心 center 和右边界 right。

    int maxLen = 0, centerIndex = 0;
    for (int i = 1; i < n - 1; i++) {
        if (P[i] > maxLen) {
            maxLen = P[i];
            centerIndex = i;
        }
    }

    int start = (centerIndex - maxLen) / 2;
    return s.substr(start, maxLen);
}

在最后一部分，我们通过遍历 P 数组来找到最长回文子串的长度和中心位置。我们初始化 maxLen 和 centerIndex 为 0，然后遍历 P 数组，如果发现某个回文串的半径长度 P[i] 大于 maxLen，就更新 maxLen 和 centerIndex 的值。

最后，我们根据中心位置 centerIndex 和回文串的长度 maxLen，计算出最长回文子串在原始字符串 s 中的起始位置 start。最终，我们使用 substr 函数从 s 中提取出最长回文子串，并将其作为函数的返回值。

当你需要根据具体要求修改代码时，可以根据以下几个方面进行调整：

  1. 记录回文串的位置：模板中只返回了最长回文子串本身，如果你还需要记录回文串在原始字符串中的位置，可以在模板中添加相应的变量和逻辑。你可以使用额外的变量来记录最长回文子串的起始位置和长度，然后根据这些信息从原始字符串中提取出回文串。
  2. 统计所有的最长回文子串：如果题目要求统计所有的最长回文子串，而不仅仅是返回一个最长回文子串，你可以修改代码来存储所有满足最长长度的回文串。你可以使用容器（如向量或列表）来存储这些回文串的起始位置和长度，然后在遍历过程中更新和添加相应的信息。
  3. 处理特殊字符或其他要求：根据题目要求，你可能需要对字符串中的特殊字符进行处理，或者进行其他特定的操作。在模板中，我们使用了特殊字符 # 来处理回文串的奇偶长度情况，但在某些情况下，你可能需要使用其他字符或进行其他处理。根据题目要求，修改代码以满足特定的需求。

在进行任何修改之前，建议先充分理解模板代码的原理和逻辑，并根据题目要求明确你需要实现的功能。然后，根据需要添加变量、数据结构和逻辑来实现所需的功能。在修改代码时，务必进行充分的测试和调试，确保修改后的代码仍然正确且符合题目要求。

✨结语

🍓🍓在本次博客中，我们讨论了求解最长回文子串的问题。首先，我们介绍了两种常用的算法：中心扩展法和马拉车算法。中心扩展法是一种简单直观的方法，通过以每个字符为中心向两侧扩展来找到回文串。而马拉车算法则是一种更高效的算法，利用回文串的对称性和已知回文串的信息来加速搜索过程。

🍓🍓我们详细讲解了马拉车算法的实现，并提供了一个标准的马拉车算法模板供参考。该模板使用了预处理和动态规划的思想，通过添加特殊字符和记录回文串的半径长度来快速计算最长回文子串。

🍓🍓此外，我们还探讨了如何根据具体要求修改马拉车算法的模板。根据题目要求，你可以记录回文串的位置、统计所有的最长回文子串，并根据特殊字符或其他要求进行相应的调整。

🍓🍓最后，我们强调了对算法的理解和测试的重要性。在使用算法模板时，确保理解每个部分的原理和逻辑，并根据具体需求进行修改。进行充分的测试和调试，确保修改后的代码仍然正确且满足题目要求。

希望本次博客对你理解最长回文子串的求解方法有所帮助，并为你在解决类似问题时提供了指导和思路。如果你有任何其他问题，我们随时欢迎帮助解答。祝你在竞赛中取得优异的成绩！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/616628.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

SpringCloud服务注册中心

SpringCloud服务注册中心

SpringCloud 服务注册中心 1.Eureka基础知识 什么是服务治理? Spring Cloud 封装了 Netflix 公司开发的 Eureka 模块来实现服务治理 在传统的rpc远程调用框架中,管理每个服务与服务之间依赖关系比较复杂,管理比较复杂,所以需要使用服务治理,管理服务与服务之间的依赖关系,…
阅读更多...
数据库的增删改查(三)

数据库的增删改查(三)

1、查询 1.1、聚合查询 1.1.1、聚合函数 数据库提供了很多函数&#xff0c;其中就包括聚合函数&#xff0c;常见的聚合函数如下表 函数说明COUNT([IDDINCT] expr)返回查询到的数据的数量SUM([DISTINCT] expr)返回查询到的数据的总和&#xff0c;不是数字没有意义AVG([IDSTI…
阅读更多...
一篇长文教你进行全方位的使用appium

一篇长文教你进行全方位的使用appium

随着移动应用的日益普及&#xff0c;移动应用的测试成为了软件开发的重要组成部分。Python&#xff0c;作为一种易于学习&#xff0c;功能强大的编程语言&#xff0c;特别适合进行这种测试。本文将详细介绍如何使用Python进行APP测试&#xff0c;并附带一个实例。 Python 和 Ap…
阅读更多...
CVE漏洞复现-CVE-2021-2109 Weblogic Server远程代码执行

CVE漏洞复现-CVE-2021-2109 Weblogic Server远程代码执行

CVE-2021-2109 Weblogic Server远程代码执行 漏洞背景 2021年1月20日&#xff0c;Oracle官方发布了漏洞补丁&#xff0c;修了包括 CVE-2021-2109 Weblogic Server远程代码执行漏洞在内的多个高危严重漏洞。CVE-2021-2109 中&#xff0c;攻击者可构造恶意请求&#xff0c;造成J…
阅读更多...
多媒体库SDL以及实时音视频库WebRTC中的多线程问题实战详解

多媒体库SDL以及实时音视频库WebRTC中的多线程问题实战详解

目录 1、概述 2、开源跨平台多媒体库SDL介绍 3、开源音视频实时通信库WebRTC介绍 4、在国产化Linux桌面系统中遇到的SDL多线程问题 5、在给WebRTC新增外部音频插件库时遇到的多线程问题 6、最后 VC常用功能开发汇总&#xff08;专栏文章列表&#xff0c;欢迎订阅&#xf…
阅读更多...
【云原生】创建容器的方法

【云原生】创建容器的方法

1&#xff09;基于现有镜像的创建 先使用现有镜像创建容器 docker run 再进入容器进行内容更新 docker exec 最后提交成新的镜像 docker commit 2&#xff09;基于模板创建 可以从本地容器导出模板文件 docker export 或者从网上下载现成的模板文件 http://openvz…
阅读更多...
C++继承相关内容（二）

C++继承相关内容（二）

目录 一.拷贝构造函数 第一种情况&#xff1a;基类没有拷贝构造函数&#xff0c;派生类也没有拷贝构造函数 结果&#xff1a; 原因&#xff1a; 第二种情况&#xff1a;基类没有拷贝构造函数&#xff0c;派生类有拷贝构造函数 结果&#xff1a; 原因&#xff1a; 第三种情况…
阅读更多...
【文生图系列】 Stable Diffusion v2复现教程

【文生图系列】 Stable Diffusion v2复现教程

文章目录 xformersbug 记录 txt2imgdiffusers参考 基础环境承接Stable Diffusion v1, 详情请见我的博文【文生图系列】 Stable Diffusion v1复现教程。然后更新pytorch和torchvision的版本&#xff0c;因为要使用GPU和xformers&#xff0c;需要下载gpu版本的pytorch。再下载ope…
阅读更多...
学习笔记之微服务（一）

学习笔记之微服务（一）

一、了解微服务 1、服务架构演变 **单体架构&#xff1a;**所有业务功能都集中在一个项目中开发&#xff0c;打成一个包部署。 优点&#xff1a;架构简单、部署成本低 缺点&#xff1a;耦合度高 分布式架构&#xff1a;根据业务拆分系统功能&#xff0c;每个业务模块独立项…
阅读更多...
微信小程序map 之个性化地图（日出日落主题）

微信小程序map 之个性化地图（日出日落主题）

微信小程序map 之个性化地图&#xff08;日出日落主题&#xff09; 个性化地图之根据日出日落时间动态变换地图主题个性化前的准备进入腾讯地址服务官网小程序开发html 代码. layer-style 编号为样式名称js代码. 注意的是&#xff0c;layer-style只能定义一次&#xff0c;所以值…
阅读更多...
Yarn【常用命令】

Yarn【常用命令】

1、yarn application 查看Application运行情况 1.1、列出所有Application yarn application -list 可以通过Web UI端来查看&#xff1a; 1.2、根据Application状态过滤&#xff1a; yarn application -list -appStates &#xff08;所有状态&#xff1a; ALL 、 NEW 、 NEW…
阅读更多...
Spring Cloud Alibaba 同时兼容dubbo与openfeign

Spring Cloud Alibaba 同时兼容dubbo与openfeign

一、前言 dubbo与springcloud都可以单独作为微服务治理框架在生产中进行使用&#xff0c;但使用过springcloud的同学大概了解到&#xff0c;springcloud生态的相关组件这些年已经逐步停更&#xff0c;这就导致在服务架构演进过程中的迭代断层&#xff0c;以至于一些新的技术组…
阅读更多...
聚合/组合

聚合/组合

谨慎使用继承的方式来进行扩展&#xff0c;优先使用聚合/组合的方式来实现。 Father类里有两个方法A和方法B&#xff0c;并且A调用了B。子类Son重写了方法B&#xff0c;这时候如果子类调用继承来的方法A&#xff0c;那么方法A调用的就不再是Father.B()&#xff0c;而是子类中的…
阅读更多...
使用kali里的dnschef进行DNS欺骗

使用kali里的dnschef进行DNS欺骗

1. 前言 DNSChef是针对渗透测试人员和恶意软件分析师的高度可配置的DNS代理。它能够精细配置哪些DNS回复以修改或简单地代理真实响应。为了利用该工具&#xff0c;您必须手动配置DNS服务器以指向DNSChef。 2. 执行参数 选项参数&#xff1a; -h,--help显示帮助信息并退出--f…
阅读更多...
C语言：计算 1! + 2! + 3! + ... + n!

C语言：计算 1! + 2! + 3! + ... + n!

题目&#xff1a; 从键盘输入一个值n&#xff0c;计算 1的阶乘 至 n的阶乘 的和&#xff0c; 如&#xff1a;输入10&#xff0c;计算 1的阶乘 至 n的阶乘 的和 --> 计算&#xff1a;1! 2! 3! ... 10! 思路一&#xff1a; 效率比较低&#xff0c;会重复计算之前计算过的…
阅读更多...
Stable Diffusion 从听说到超神日记

Stable Diffusion 从听说到超神日记

1.安装模型&#xff08;B站搜秋叶&#xff09; 2.下载模型&#xff0c;安装好的界面有模型下载 有了上面模型已经可以根据模型风格去生成一些照片了 3.使用Additional Networks/lora模型 模型大多都是继承了很多网友自行训练的图库模型&#xff0c;各类风格都有&#xff01; …
阅读更多...
分享一个卡通人物

分享一个卡通人物

这几天较忙&#xff0c;像它一样&#xff1a; 代码在这里&#xff1a; <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>卡通打字</title><script src"https://s3-us-west-2.amazonaws…
阅读更多...
《MySQL（五）：基础篇- 多表查询》

《MySQL（五）：基础篇- 多表查询》

文章目录 5. 多表查询5.1 多表关系5.1.1 一对多5.1.2 多对多5.1.3 一对一 5.2 多表查询概述5.2.1 数据准备5.2.2 概述5.2.3 分类 5.3 内连接5.4 外连接5.5 自连接5.5.1 自连接查询5.5.2 联合查询5.6.2 标量子查询5.6.3 列子查询5.6.5 表子查询 5.7 多表查询案例 5. 多表查询 我…
阅读更多...
【Sql】根据字段分组排序，取其第一条数据

【Sql】根据字段分组排序，取其第一条数据

【Sql】根据字段分组排序&#xff0c;取组内第一条数据 【一】问题描述【二】解决方案&#xff08;oracle和mysql都可用&#xff09;【三】总结 【一】问题描述 &#xff08;1&#xff09;问题描述 有时候我们需要对数据进行去重处理&#xff0c;例如查询结果里的文件名有重复…
阅读更多...
常用模拟低通滤波器的设计——契比雪夫I型滤波器

常用模拟低通滤波器的设计——契比雪夫I型滤波器

目录 常用模拟低通滤波器的设计——契比雪夫I型滤波器 1、cheb1ap 函数 2、cheb1ord 函数 3、cheby1函数 4、实例演示 常用模拟低通滤波器的设计——契比雪夫I型滤波器 巴特沃斯滤波器的频率特性曲线在通带和阻带内&#xff0c;幅度特性是单调下降的&#xff0c;如果阶次一…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023