前言
学习的时候感觉要学一下张量,在B站看了一个视频,记录一下,参考的是B站视频【机翻】张量分析入门 (Tensor For Beginner)
- 前言
- 1. 张量的定义 Tenson Definition
- 2. 张量的前向和后向的转换 Forward and Backward Transformation
- 3. 向量 Vector
- 4. 余向量 Covector
- 5. 线性映射 Linear Map
- 6. 度规张量 The Metric Tensor
- 7. 张量积 Tensor Product
- 8. 张量积空间 Tensor Product Space
- 9. 张量指标的上升和下降 Raising or Lowing Indexes
1. 张量的定义 Tenson Definition

引入:一只铅笔,我们让它朝着门的方向,铅笔的朝向是始终不变的(这是本质的东西),但是铅笔在不同坐标系下的坐标却不一样(哦,可能需要进行坐标变换)。

张量是不变的,但是它的坐标在不同的坐标系下是不同的(张量的坐标定义)。

张量:向量和共变向量的组合使用张量积进行定义。

一个很直观的抽象张量的方法是从微积分的求偏导和梯度得到——雅克比矩阵。
2. 张量的前向和后向的转换 Forward and Backward Transformation
有点类似机器人学的坐标转换,旧坐标系和新坐标系的互相转换。
前向的转换(旧坐标系转换到新坐标系)

后向的转换(新坐标系转换到旧坐标系)
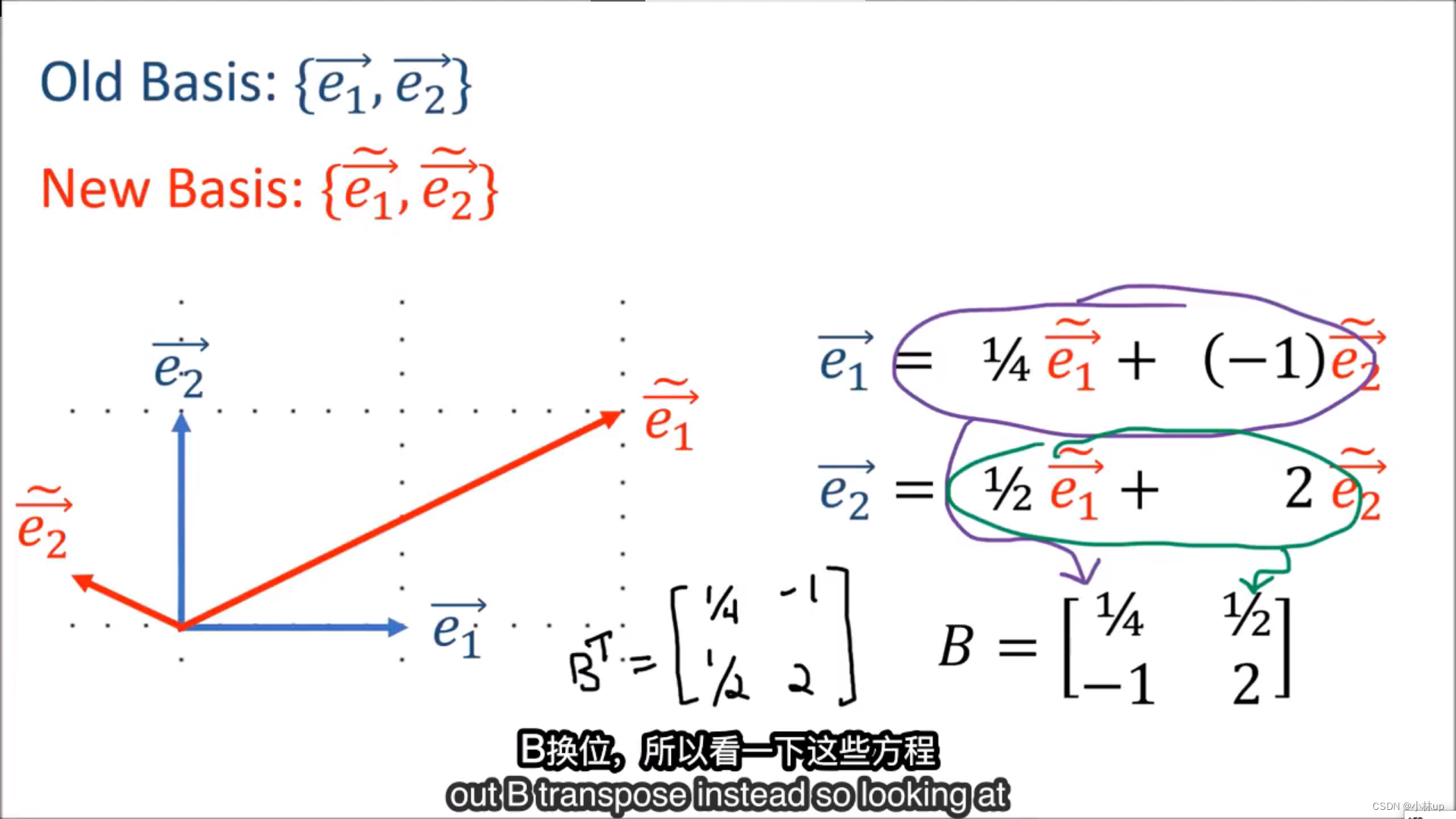
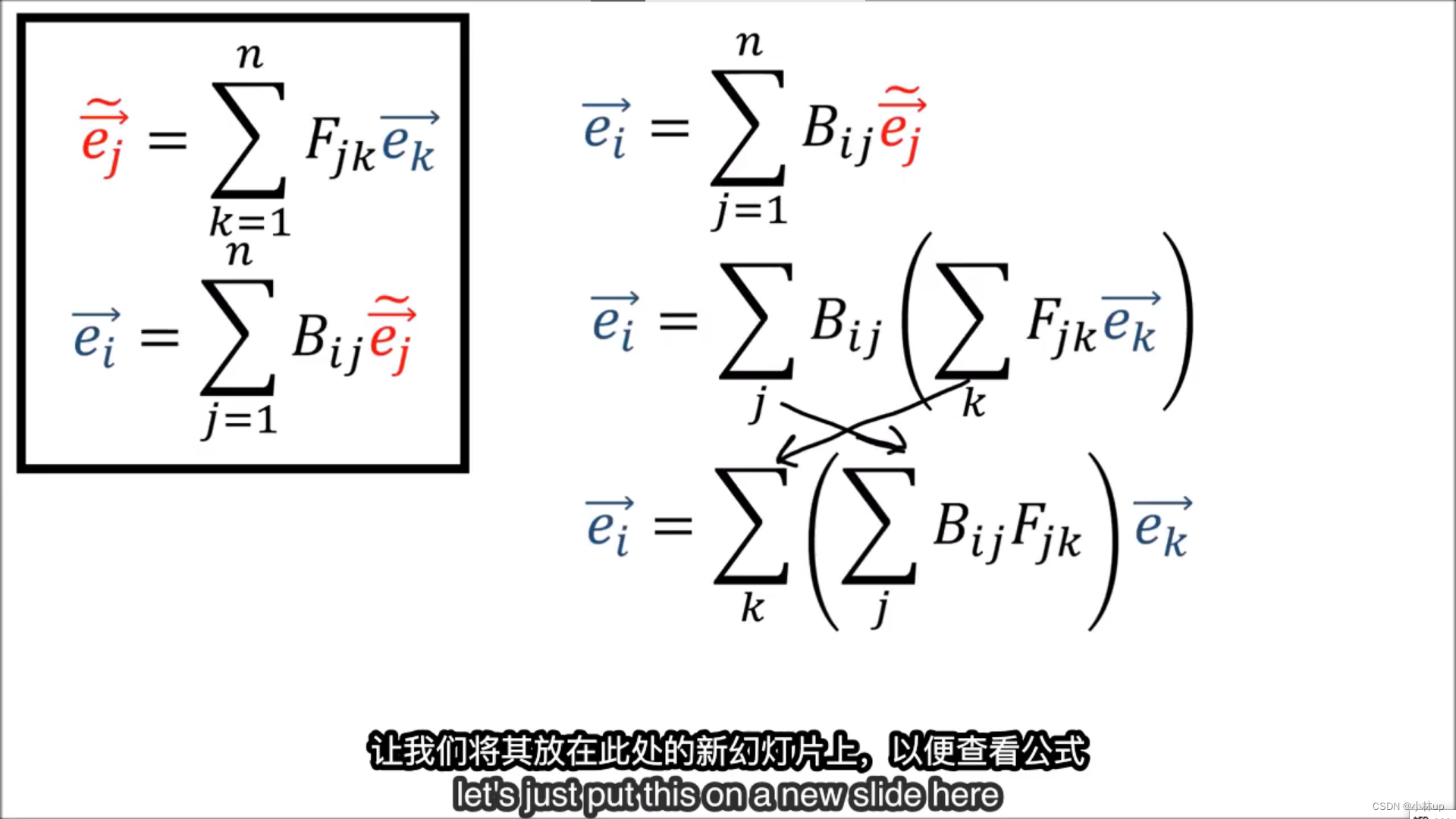
我们可以容易验证上面的正向和反向的转换矩阵互为逆矩阵。即 B F = I BF=I BF=I
高维的情况:


于是在高维的情况下我们也可以证明
B
F
BF
BF相乘的矩阵是单位阵。
【上面图片 F j k F_{jk} Fjk为 F k j F_{kj} Fkj, B i j B_{ij} Bij为 B j i B_{ji} Bji,作者说ppt写错了】
总结:最后就可以引出Kronecker Delta记号
δ
i
k
\delta_{ik}
δik。
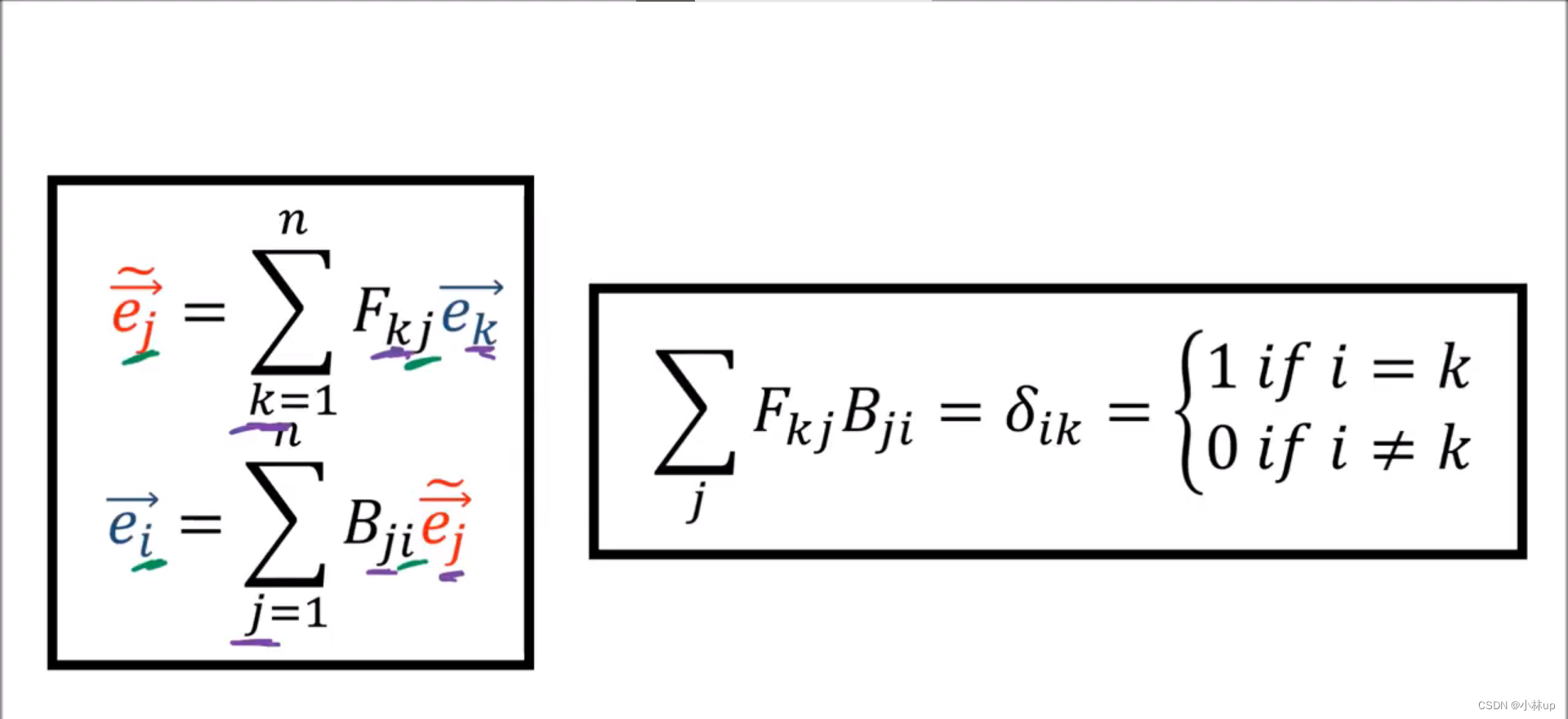
3. 向量 Vector

引入了向量空间,需要定义一个集合,并且定义向量内部的元素类型(比如是一个实数),向量的运算性质(数乘和加法)。
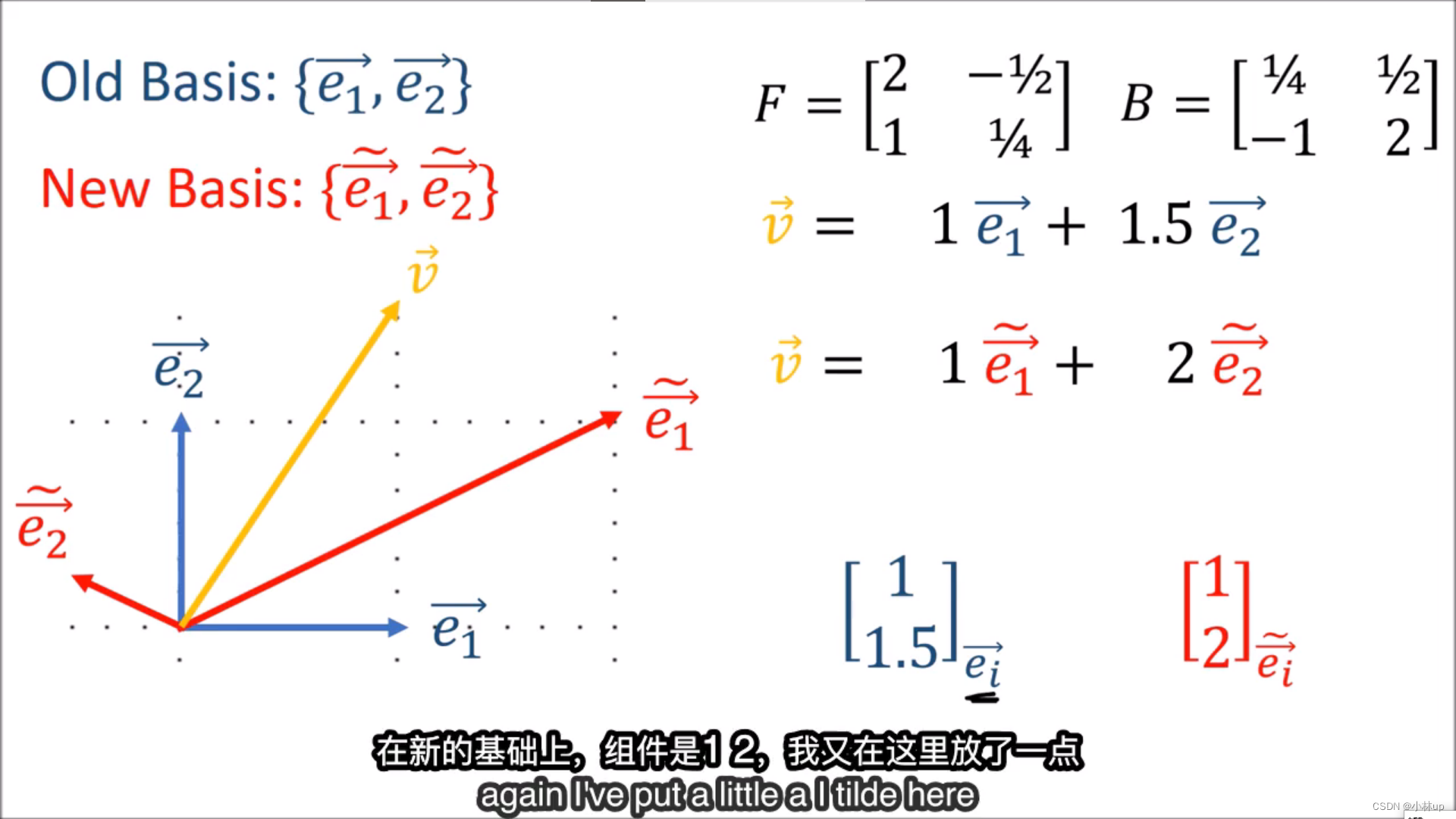

向量的正反变换为B和F,坐标的对应正反变换为F和B。

两个例子:
- 例子1:不同基向量下的坐标(只使用数乘)
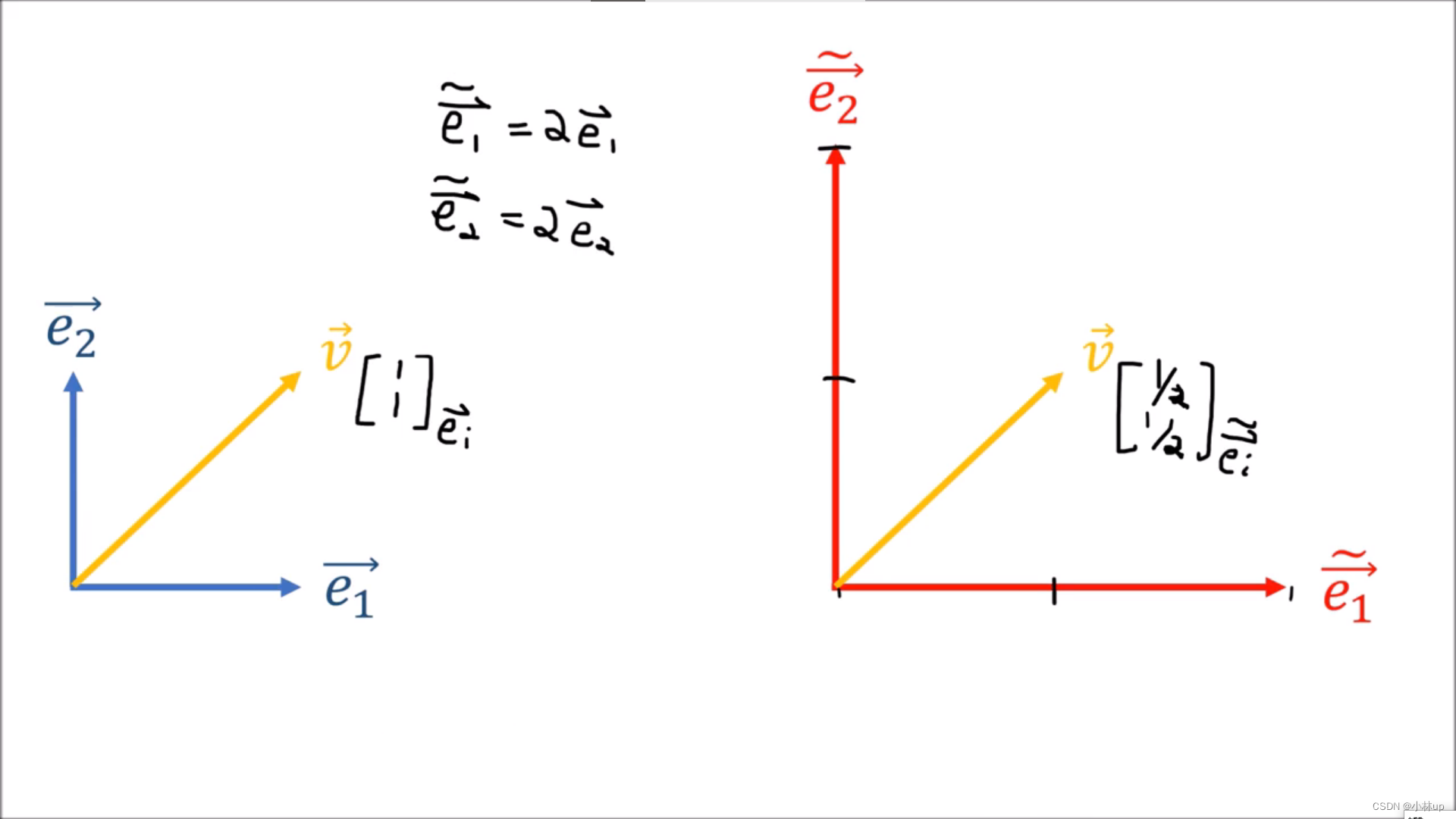
基向量长度增加了,坐标的值减少了。
- 例子2:不同基向量下的坐标(基向量旋转)
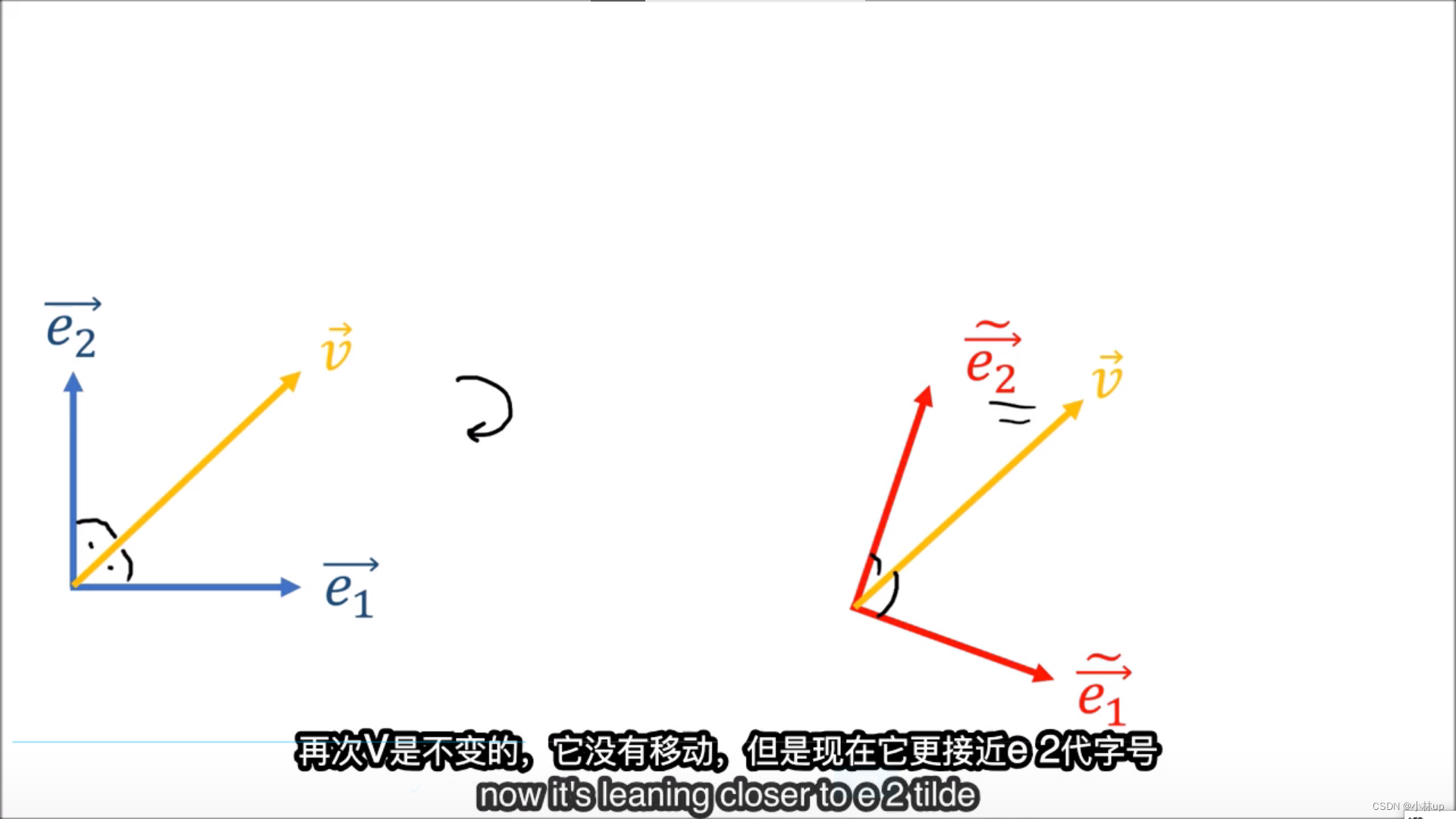
基向量长度不变进行顺时针旋转,相对的向量坐标的变化是相对原来的坐标系逆时针旋转,更接近 e 2 ⃗ \vec{e_2} e2,变化方向也是相反的。


基向量和向量分量的变换公式:
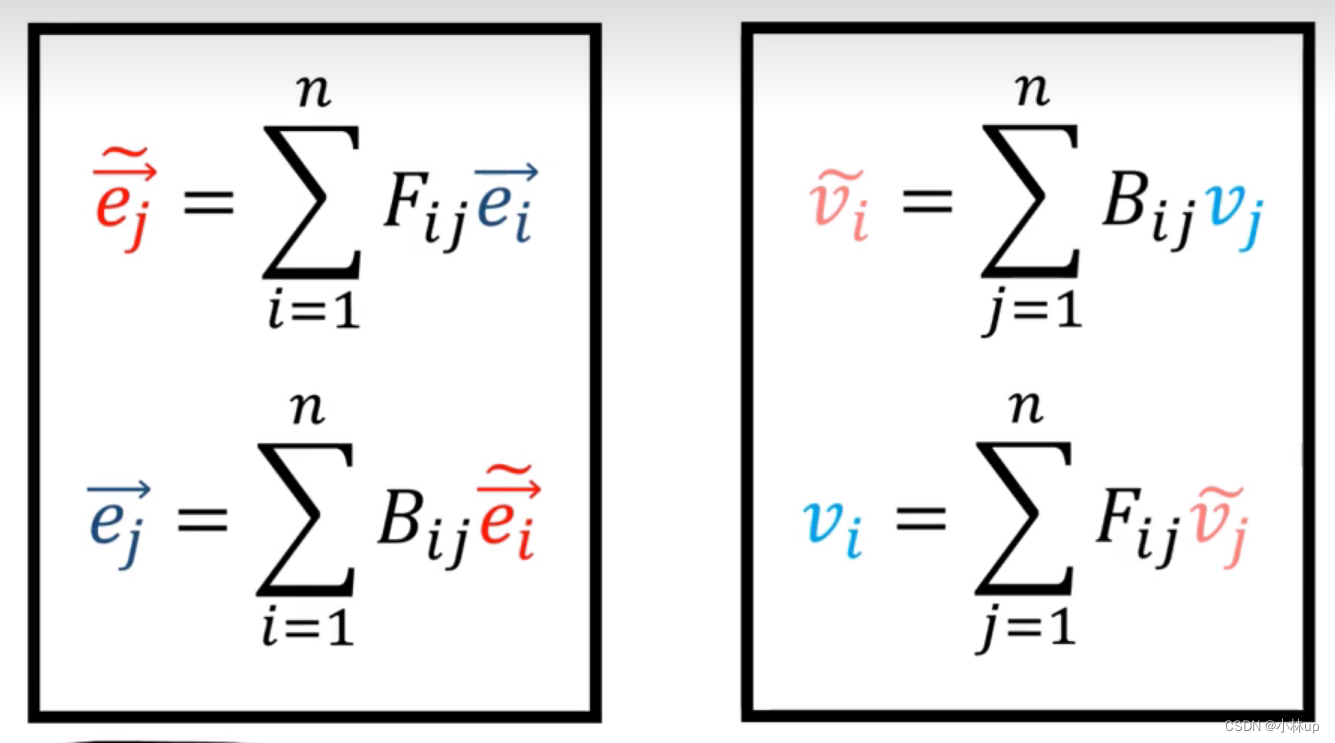
这个时候基向量分量和向量是相反的关系,我们称他是contravariant 的。
为了区分这种相反的关系,我们需要把放在向量分量的下标改为上标,提示我们它是逆变张量(当基向量变大时,对应的向量分量变小)。
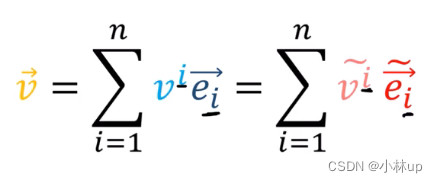
4. 余向量 Covector
我们可以基本认为余向量是一个行向量。它相当于一个函数(矢量的点积)将列向量转化为一个实数:

验证加法:

验证数乘:


这个函数相当于是一个线性函数。
我们可以将这个过程进行一个可视化。
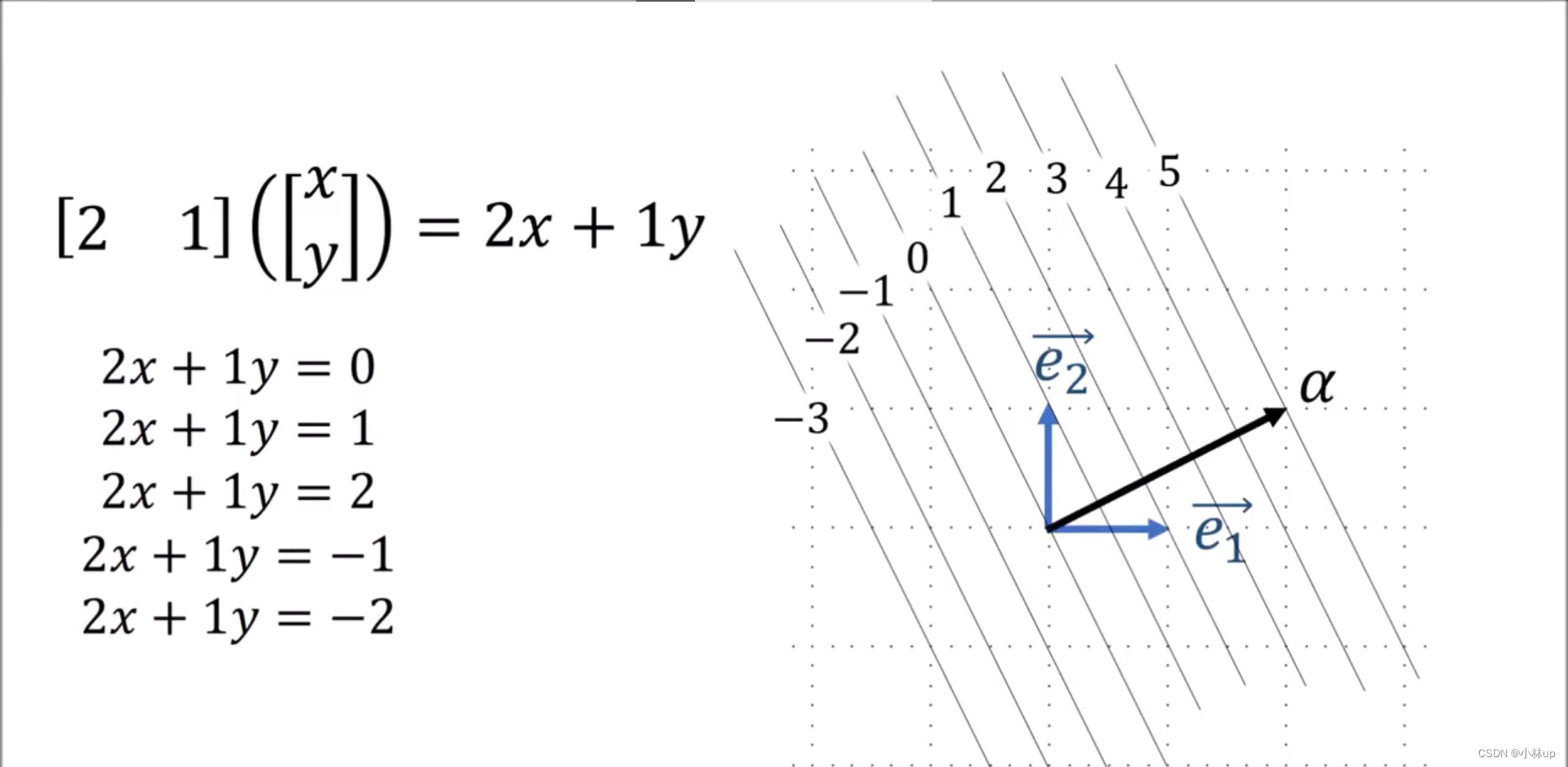

作用以后相当于求向量落在那条线上(有点类似于等高线)。
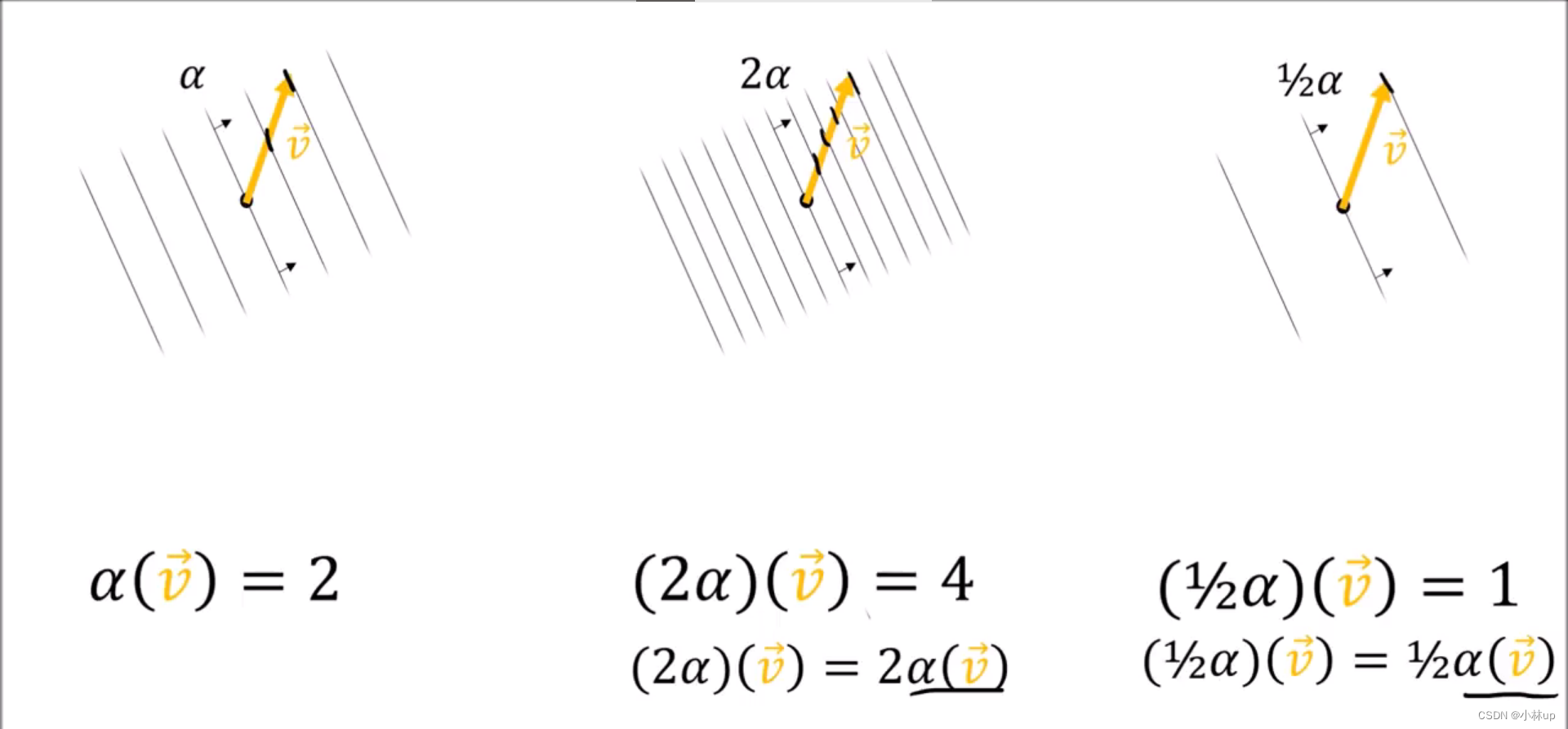
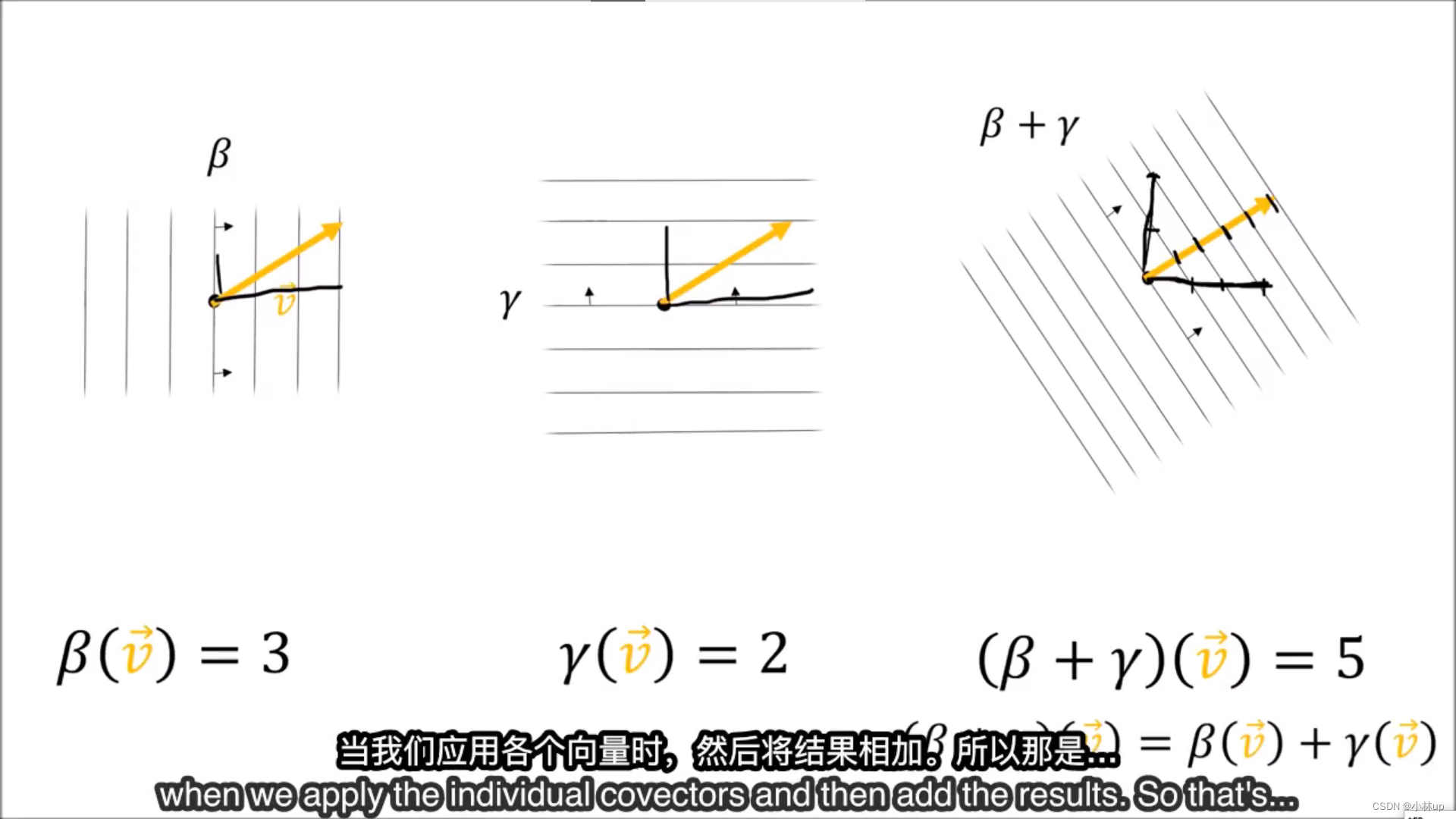
余向量有很好的数乘和加法的性质。它所在的空间可以看做是向量空间的一个对偶空间。(加法和数乘的定义不一样)

最后做一个总结:
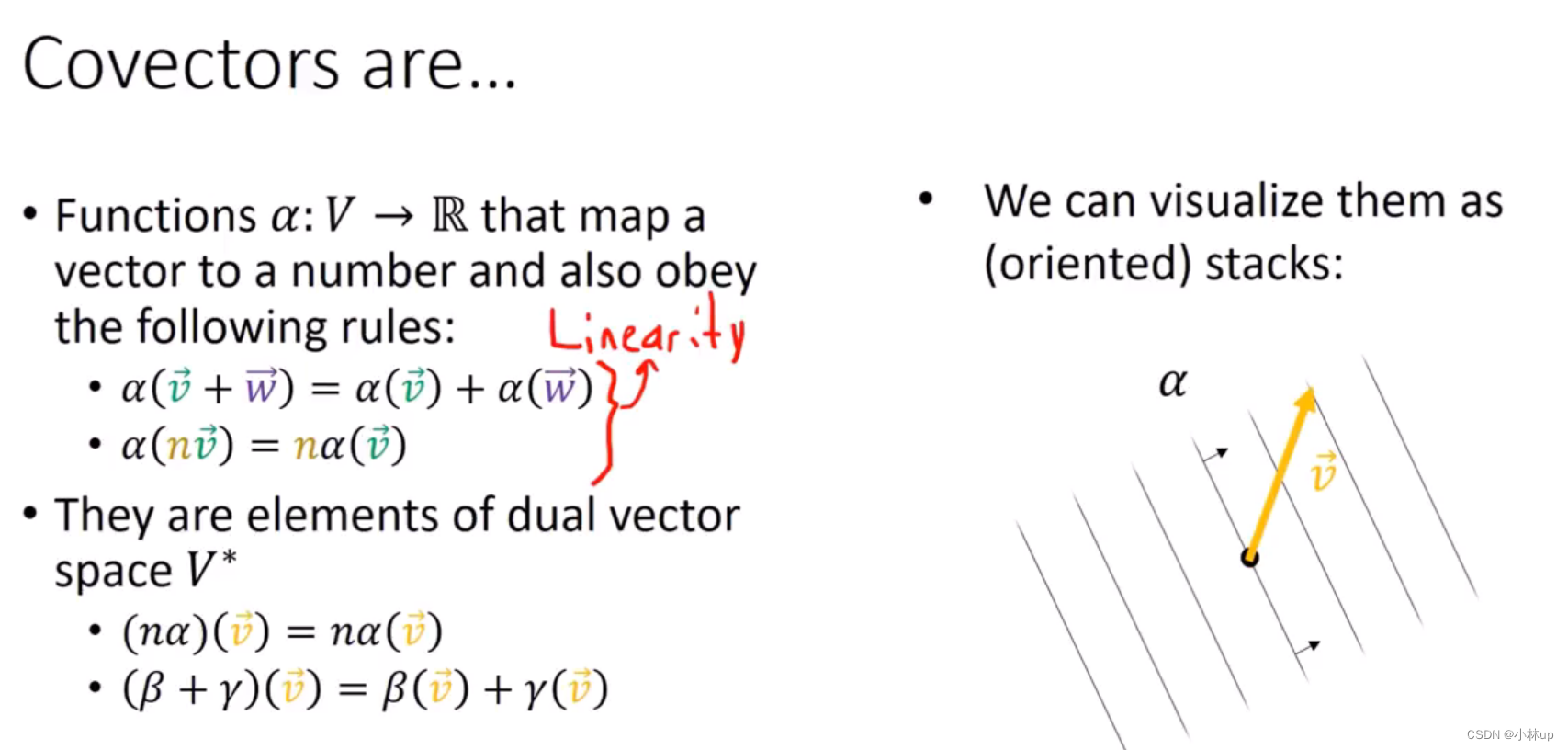
我们可以理解为Covector协变张量就是行向量,而其向量分量是这个协变张量作用在列向量(点积)。

注意
- 协变张量相当于一个函数关系: α : V ↦ R \alpha:V \mapsto\R α:V↦R
- 协变张量不存在于向量空间 V V V中
- 我们不能像向量一样使用基向量 { e 1 ⃗ , e 2 ⃗ } \{\vec{e_1},\vec{e_2}\} {e1,e2}对协变张量进行测量。

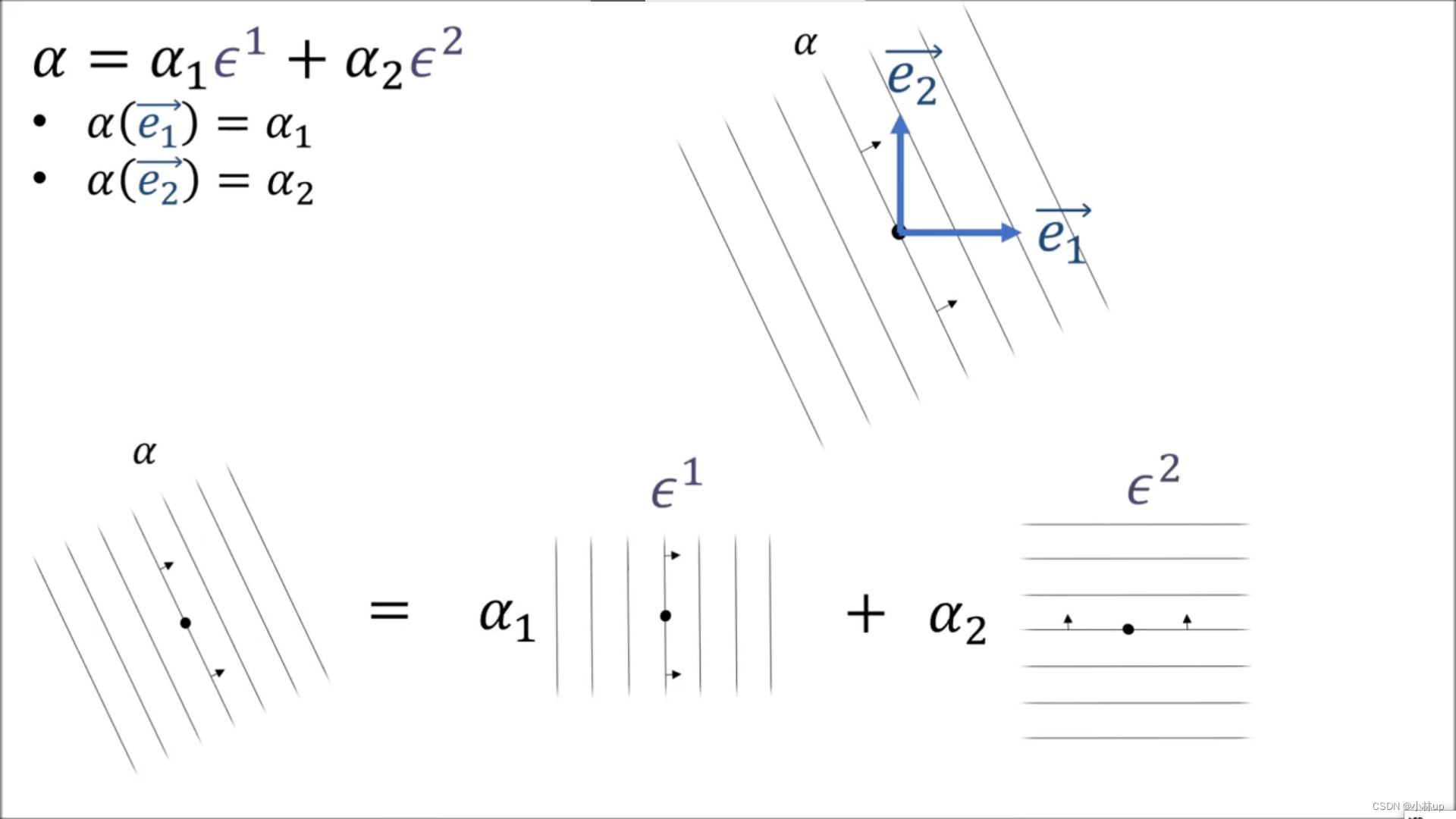
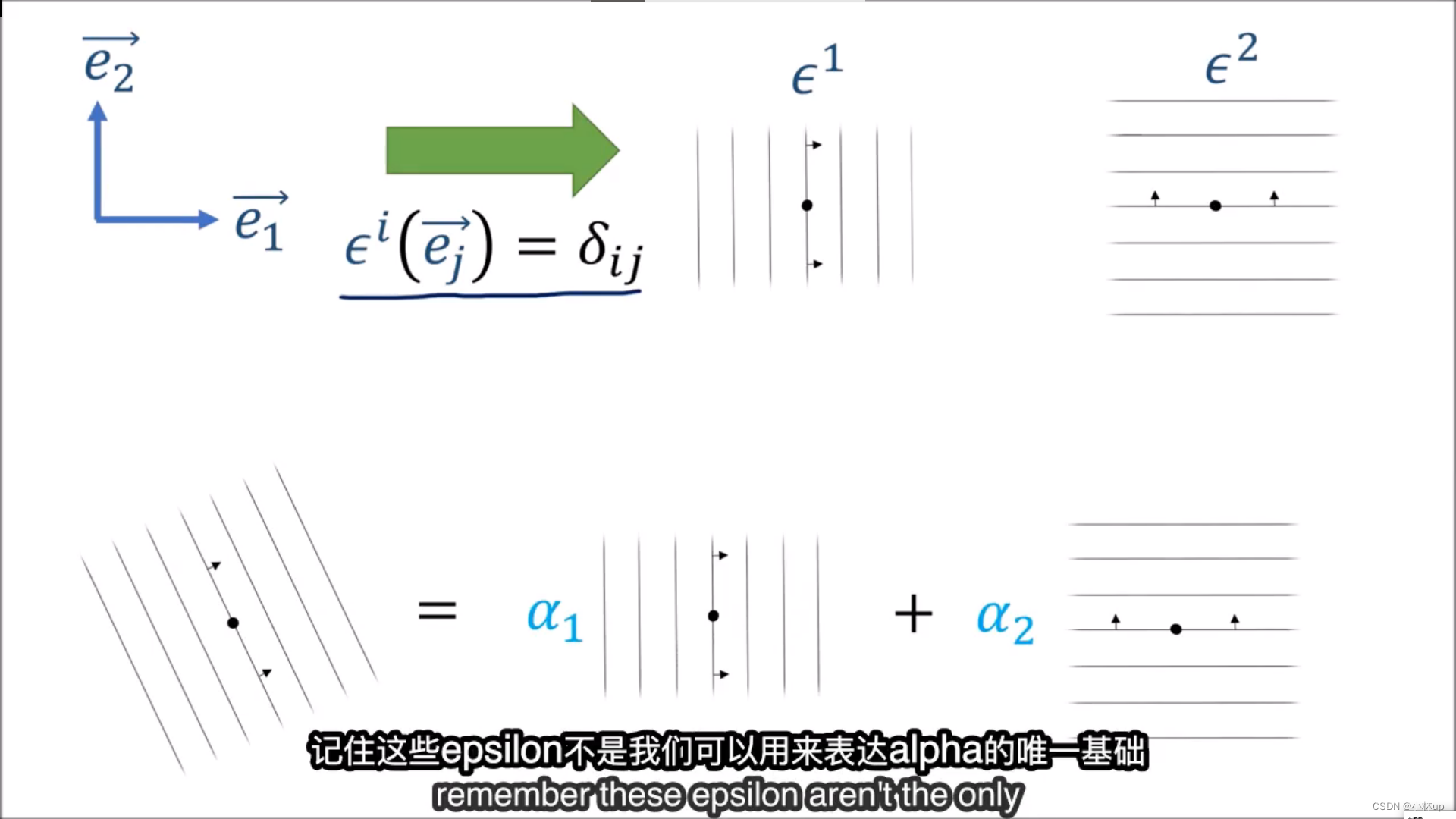
我们引入一个记号 ϵ \epsilon ϵ作为对偶基,并按上图进行定义,这样又可以引入Kronecker Delta记号 δ i k \delta_{ik} δik。

ϵ \epsilon ϵ的作用是将向量投影到协变张量的方向。

协变张量
α
\alpha
α相当于定义了一个对偶基。几何直观是:
这里又引入Kronecker Delta记号
δ
i
k
\delta_{ik}
δik。
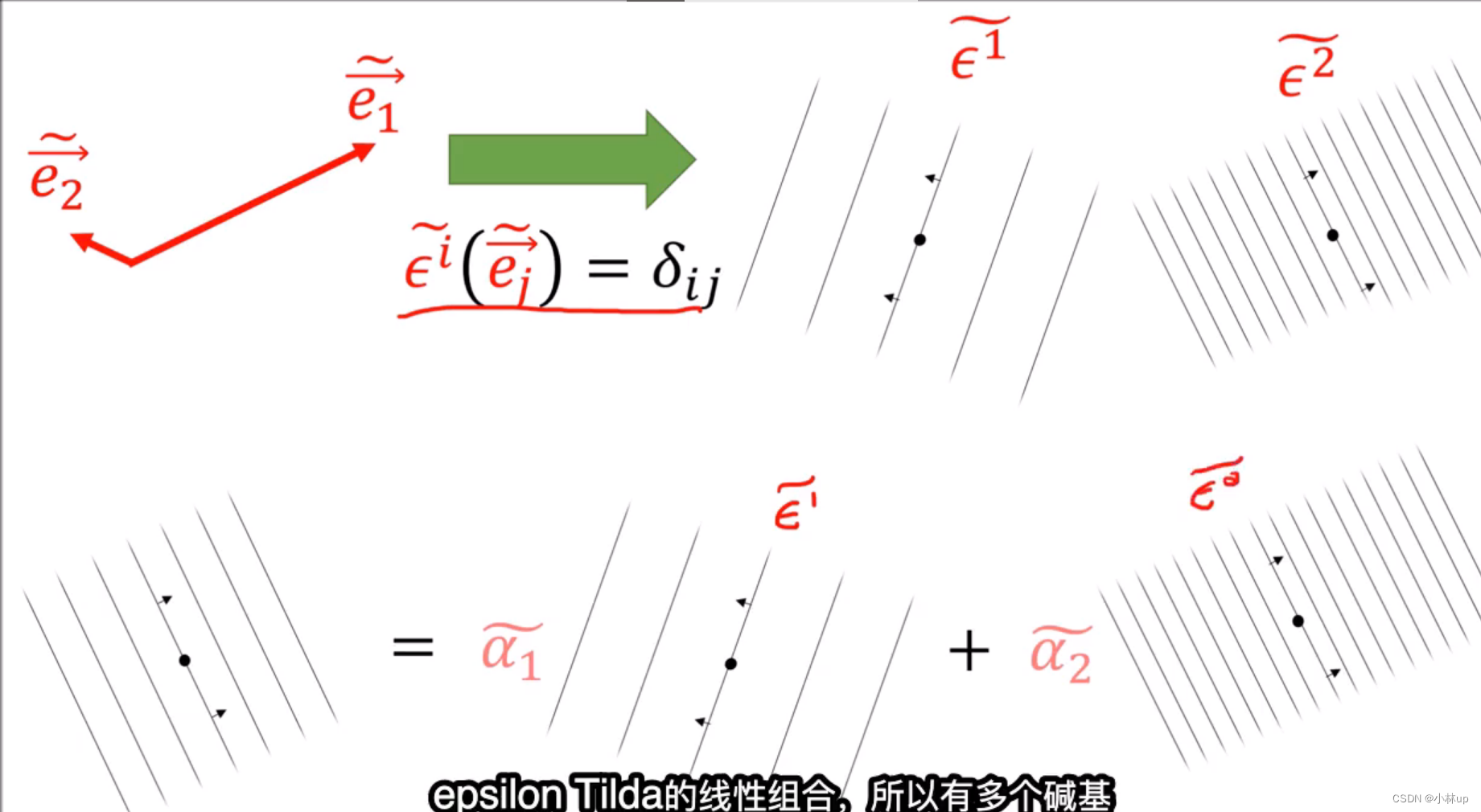
协变张量可以有不同的表达方式
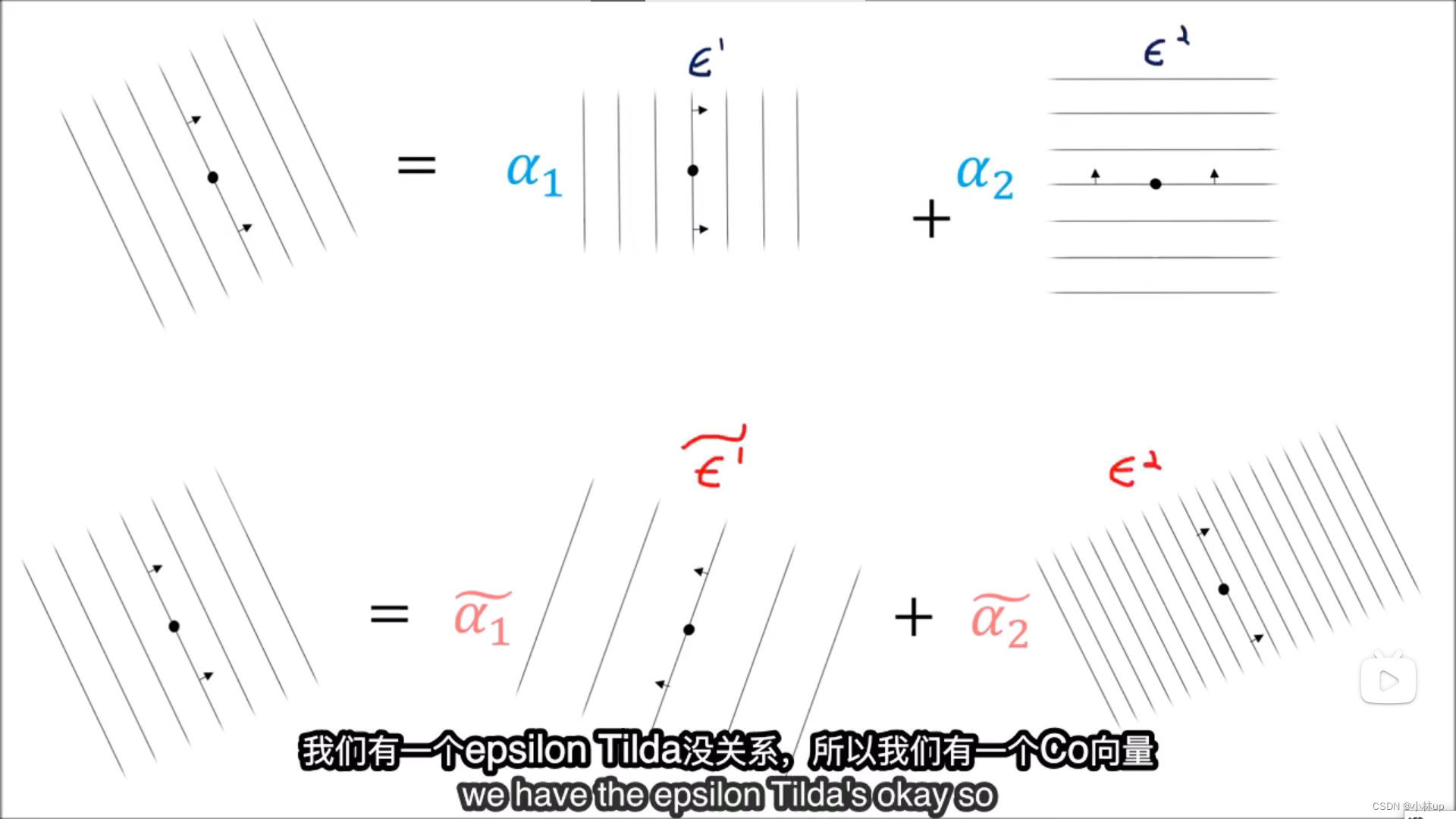

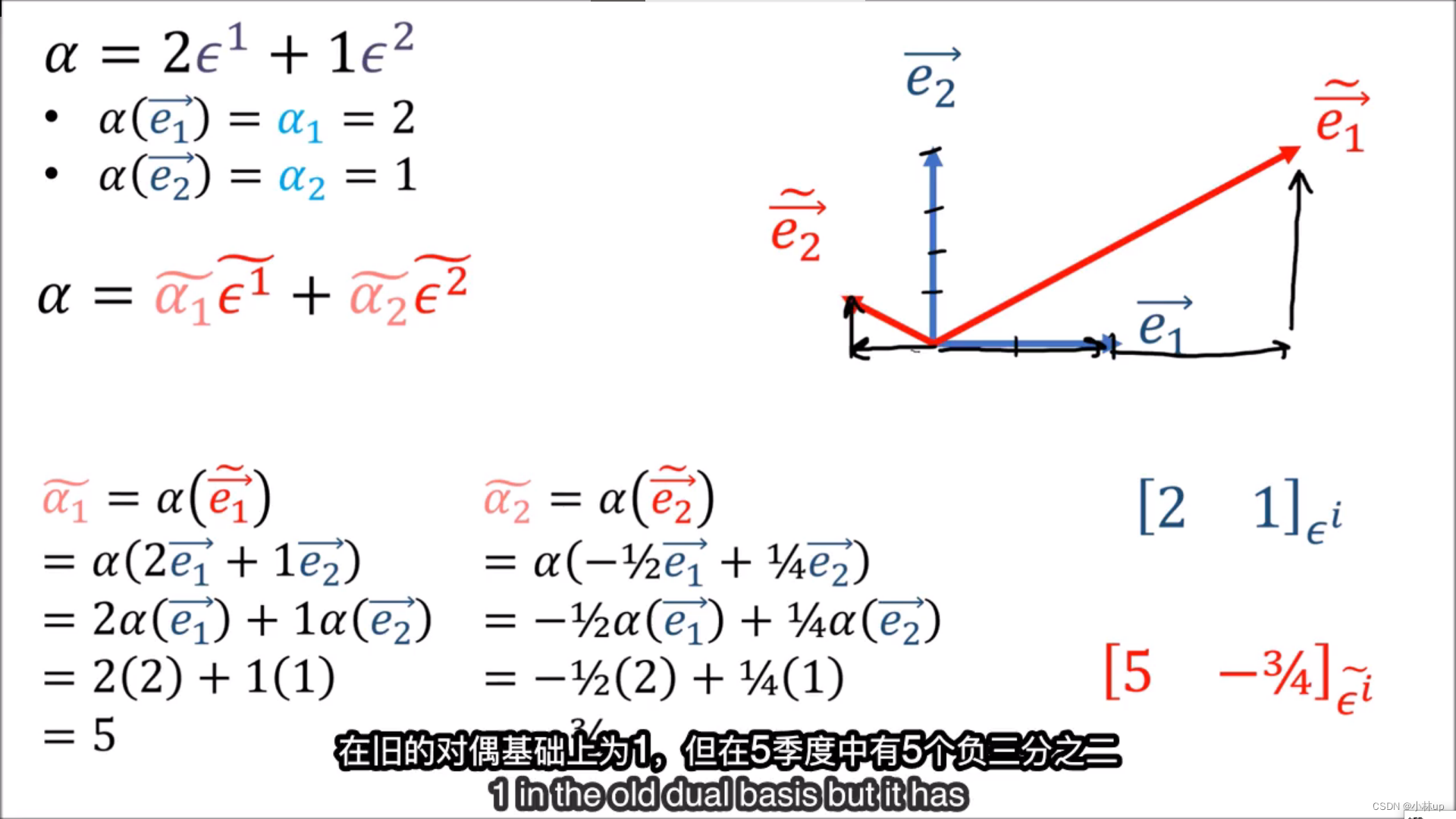

协变张量可以看到坐标分量:
2
×
2
+
1
×
1
=
5
2\times 2+1\times 1=5
2×2+1×1=5
坐标(旧坐标换到新坐标):
2
e
1
+
1
e
2
=
e
~
1
2\mathbf{e}_1+1\mathbf{e}_2={\mathbf{\tilde{e}}}_1
2e1+1e2=e~1
都是同样的变大,不存在逆变张量。
这和前面讲的逆变张量有很大的区别:旧坐标分量到新坐标分量在逆变张量用的是
B
B
B进行变换,反之用
F
F
F;旧坐标分量到新坐标分量在协变张量用的是
F
F
F进行变换,反之用
B
B
B。

我们可以看看协变张量的计算规则:


ϵ
\epsilon
ϵ是对偶基,而
e
e
e是原始基。我们可以看到旧对偶基
ϵ
\epsilon
ϵ到新对偶基
ϵ
~
\tilde{\epsilon}
ϵ~的系数矩阵和原始基
e
~
\tilde{e}
e~到新基
e
e
e的系数矩阵差一个转置。
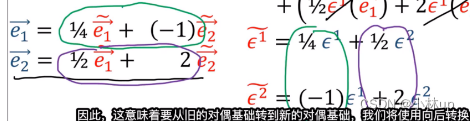
对于高维的情况,我们有:

因为 Q F = I QF=I QF=I, B F = I BF=I BF=I,所以 Q = B Q=B Q=B。这就是说从旧的对偶基变换到新的对偶基需要使用 B B B(反向传递进行变换)。于是我们就知道 ϵ \epsilon ϵ需要使用上标,因为它和基向量 e e e的变换方向是相反的。
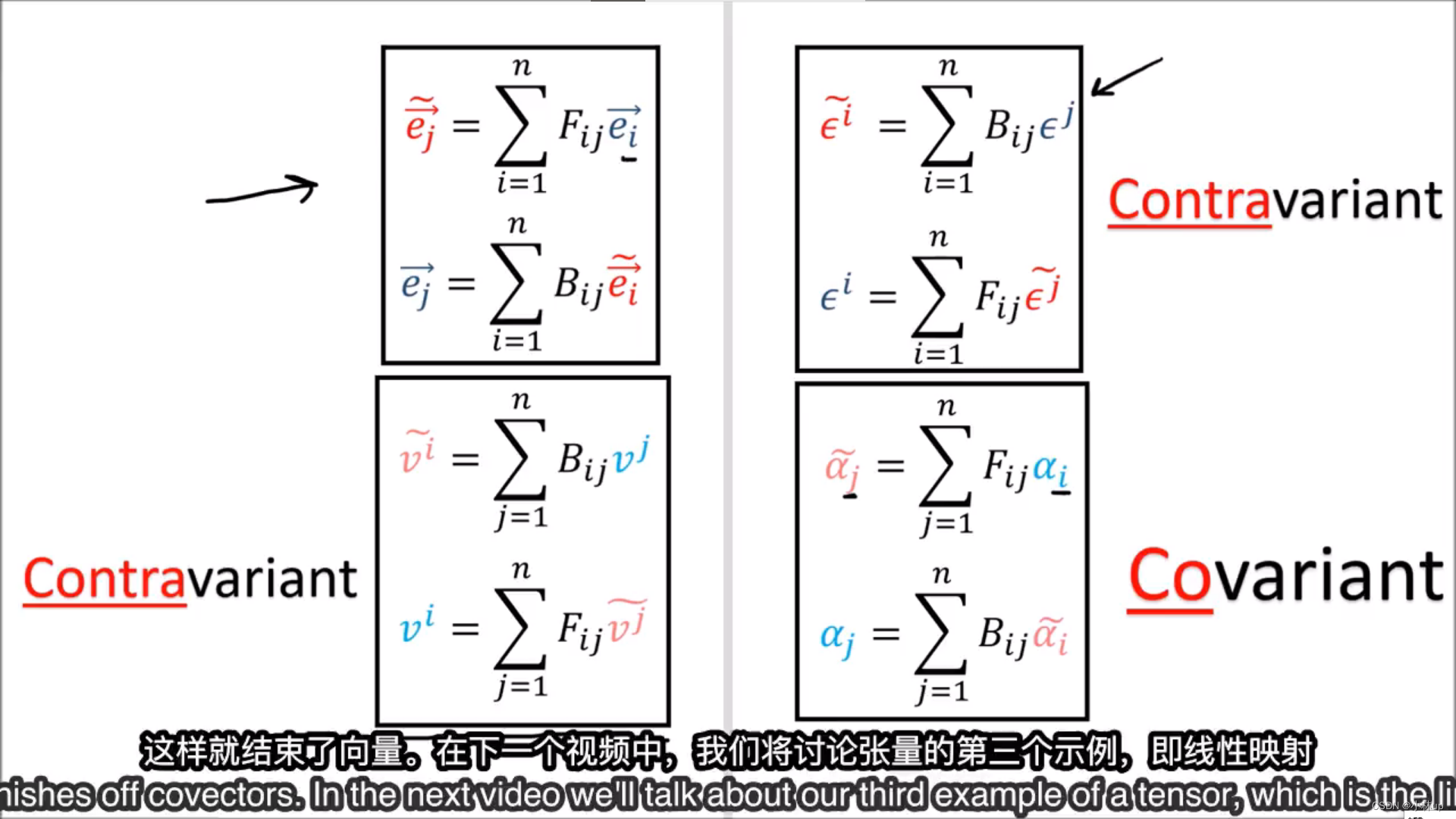
这是基向量和对偶向量之间的变换关系,它们的变换规则是完全相反的。
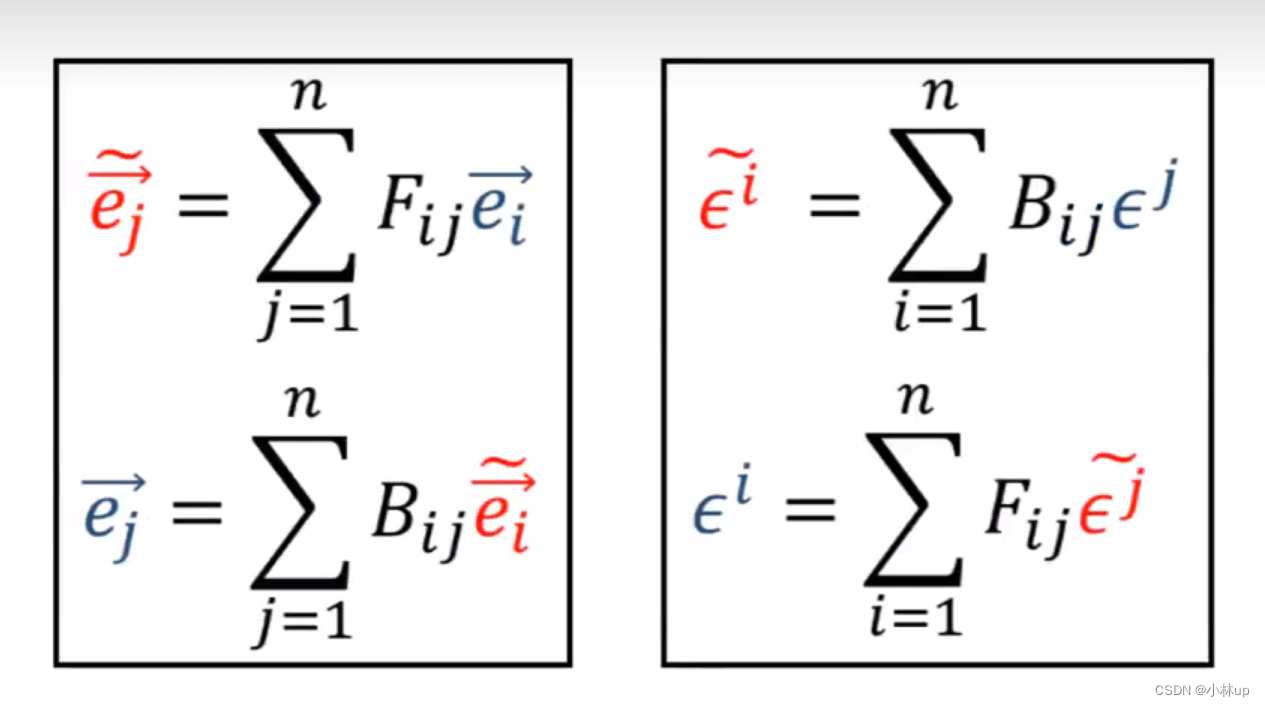
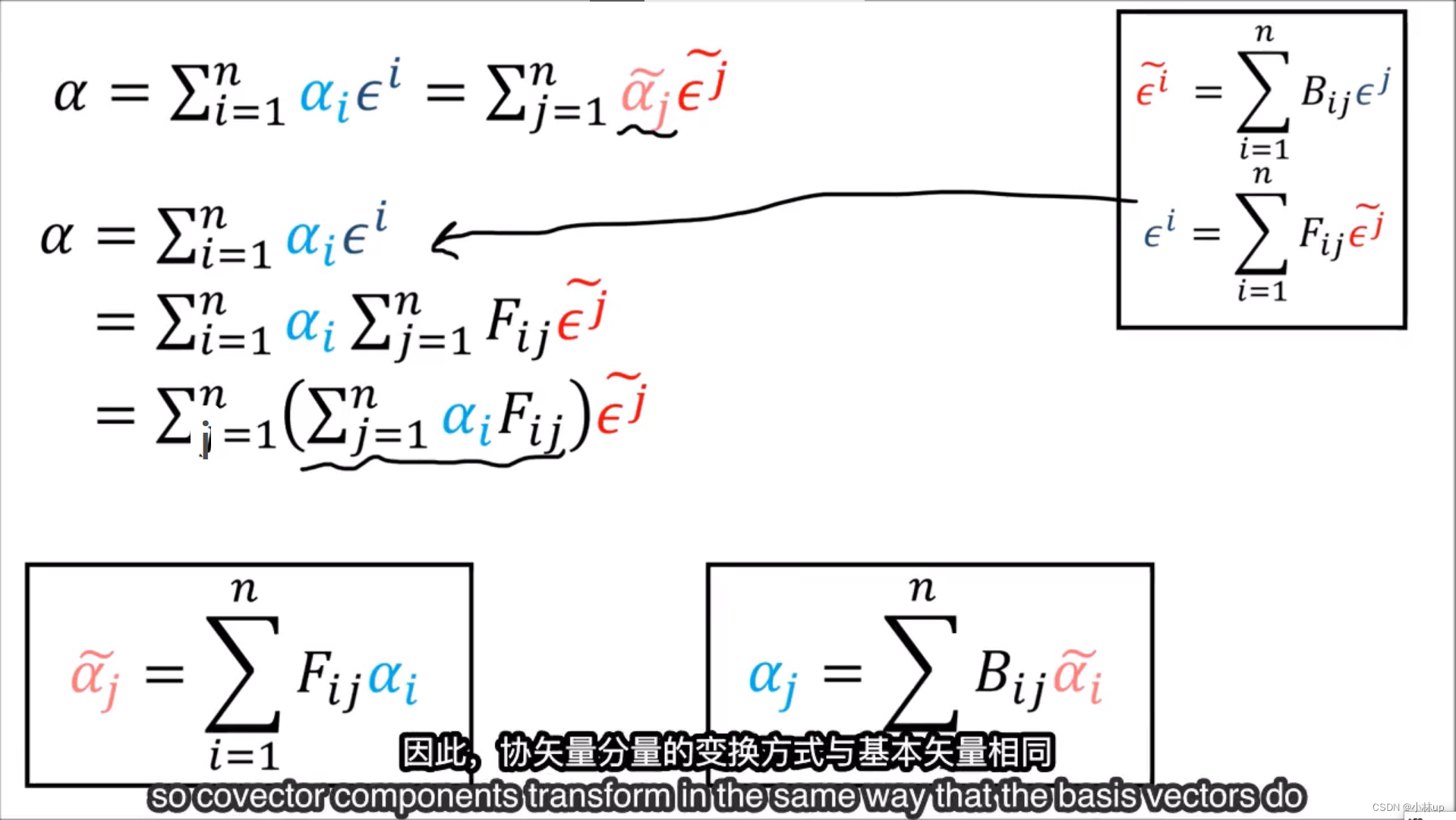
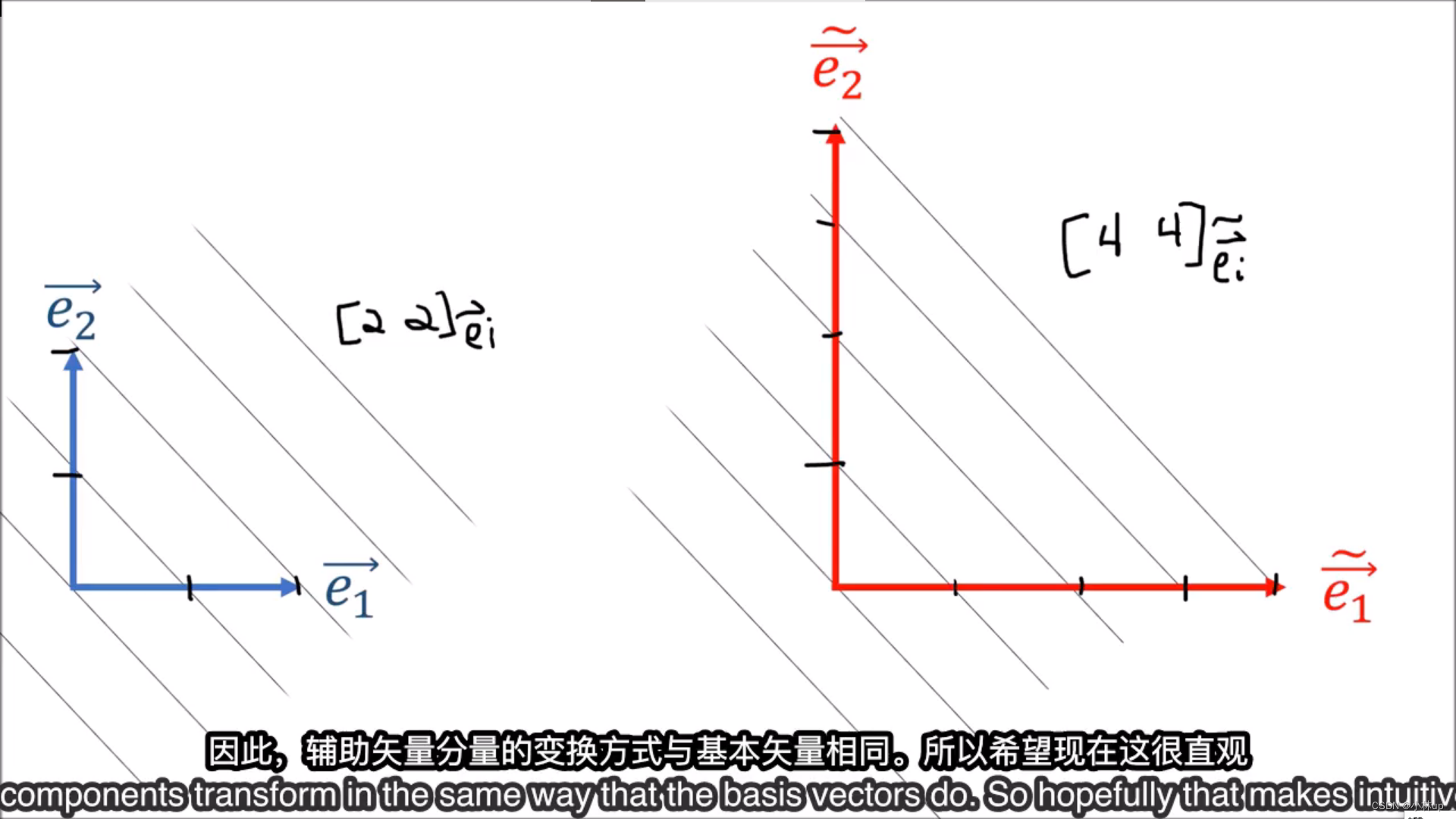
基向量变大,对应的向量分量也会变大。
下面这张图总结了前面所讲的协变和逆变变换。
5. 线性映射 Linear Map
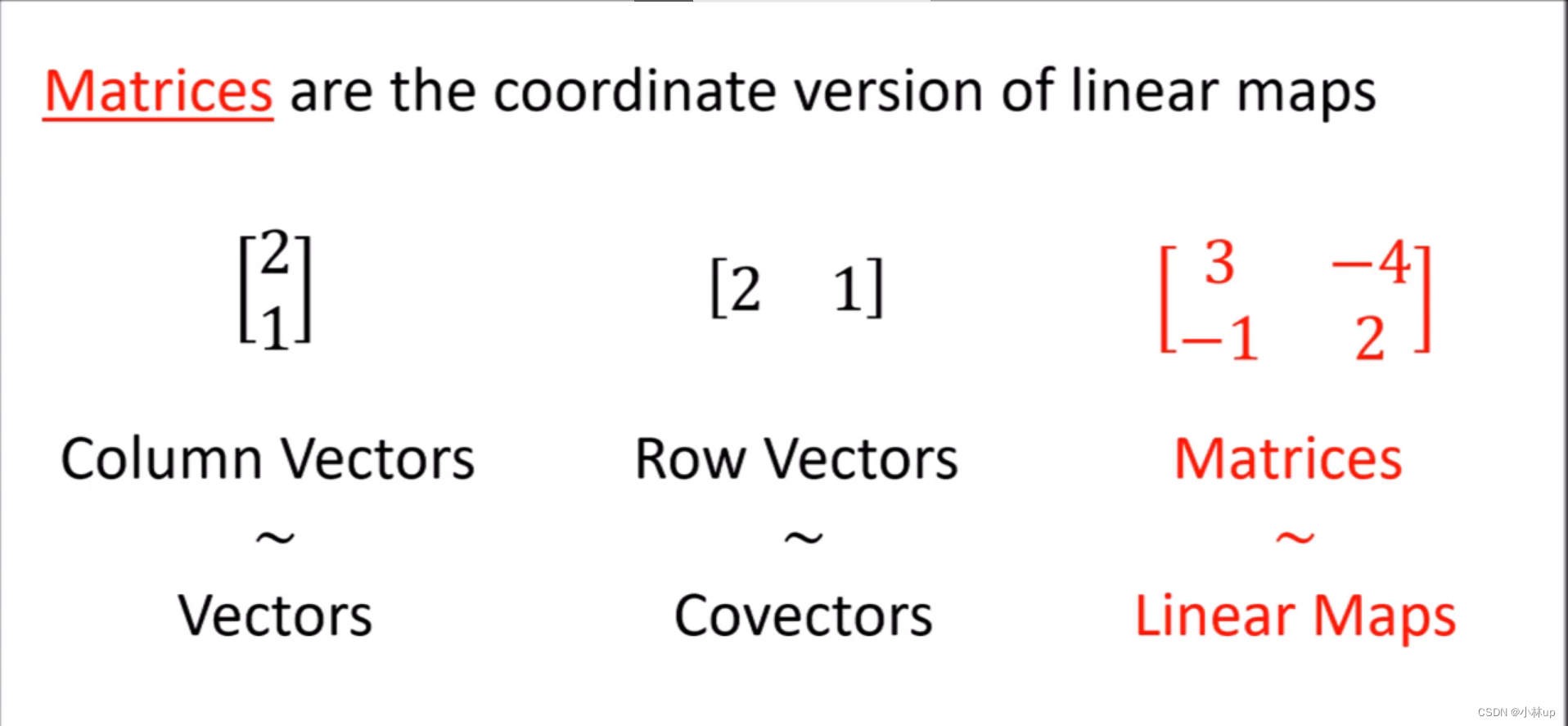
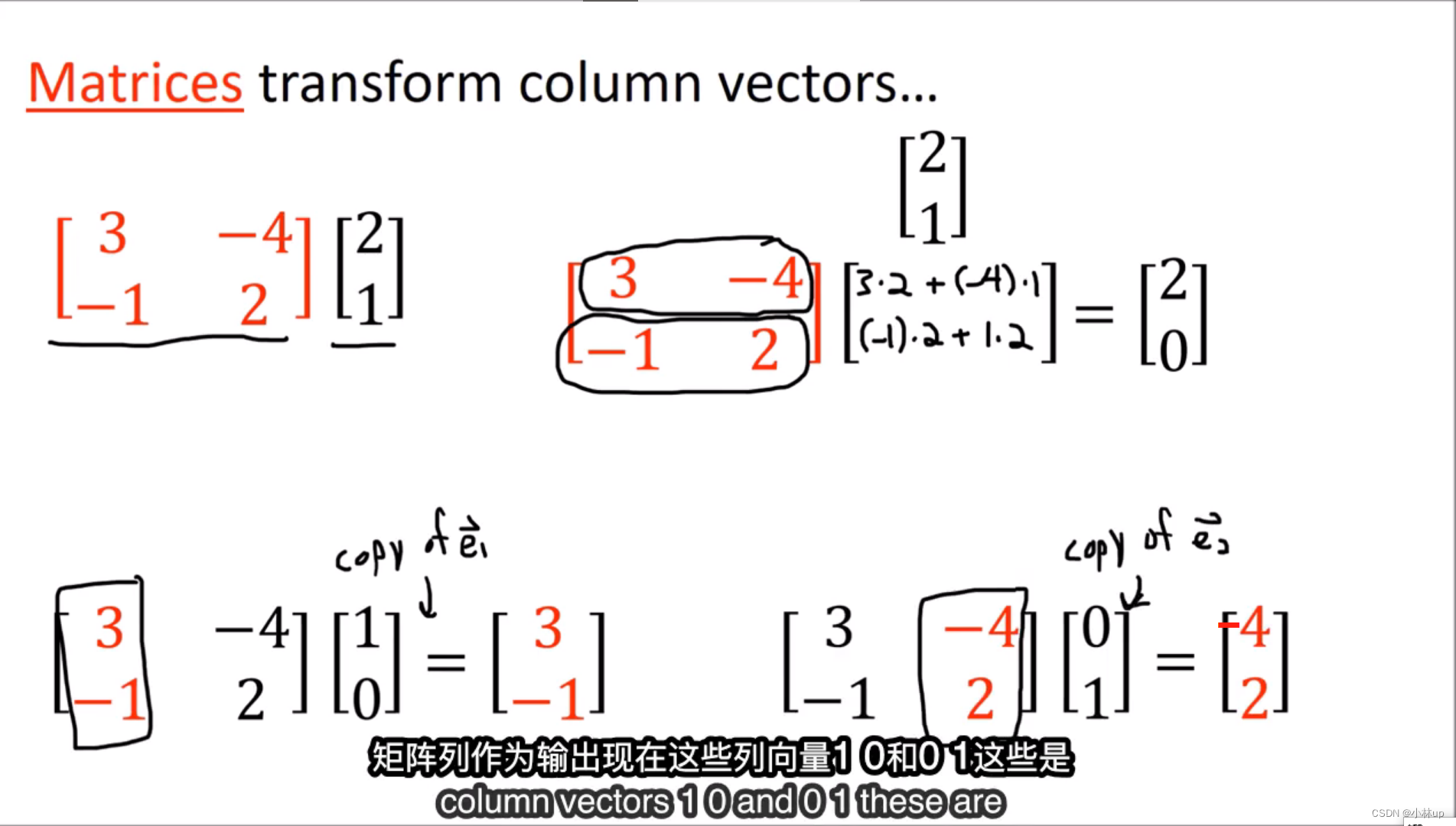
线性映射转换输入的向量,但是不会转换基。几何直观上进行了这样的转换:
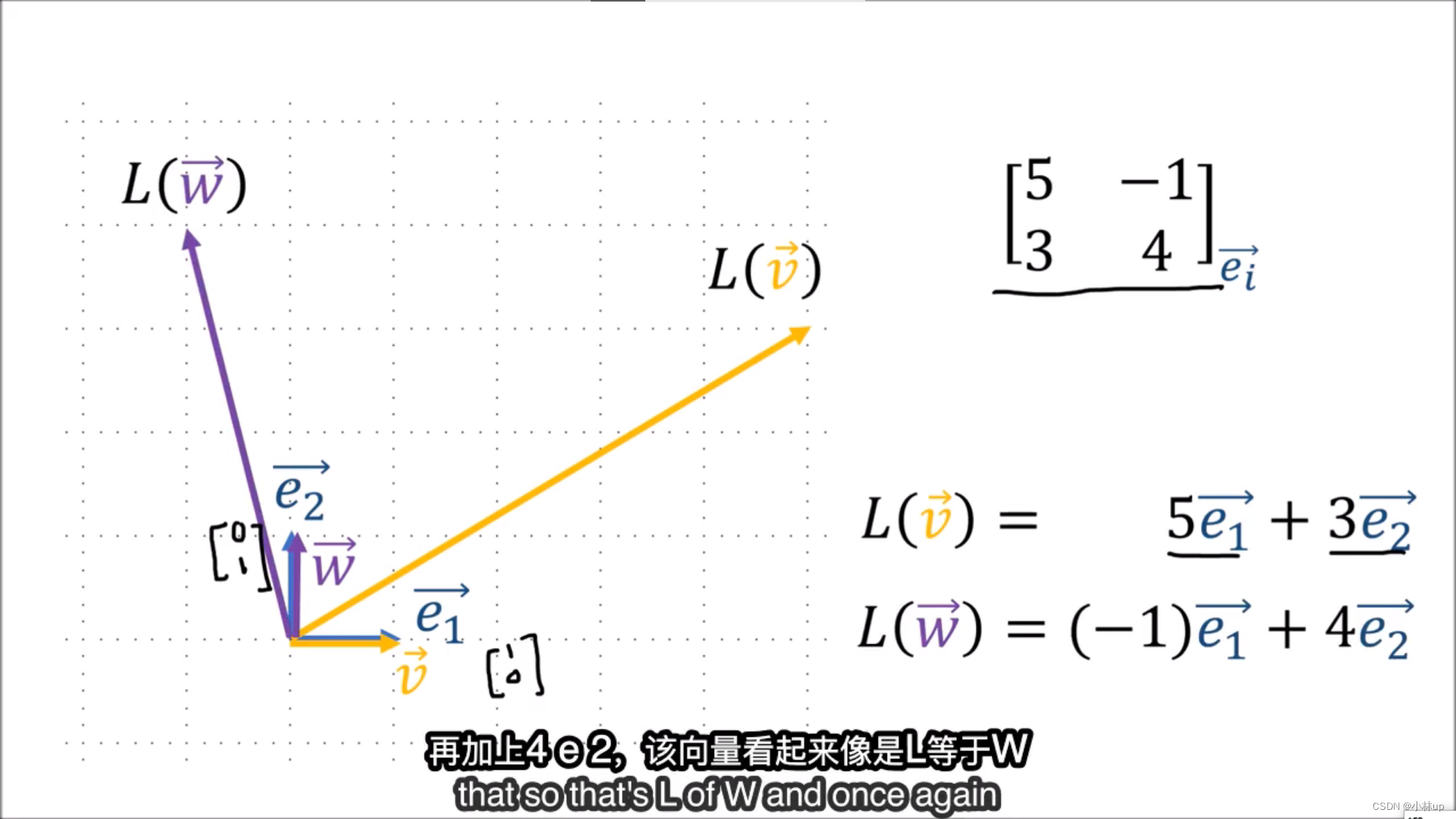

尽管输入和输出的向量可能是不一样的,但是它们都是在同一组基下进行表示的。

在线性变换的作用下,网格线仍然是平行的,均匀分布的,而且原点是不变的。但是平移不是线性变换,因为原点的位置发生了改变。

线性映射需要满足以上三点。其中后两点被称为是线性性。
加法的几何直观:

数乘的几何直观:
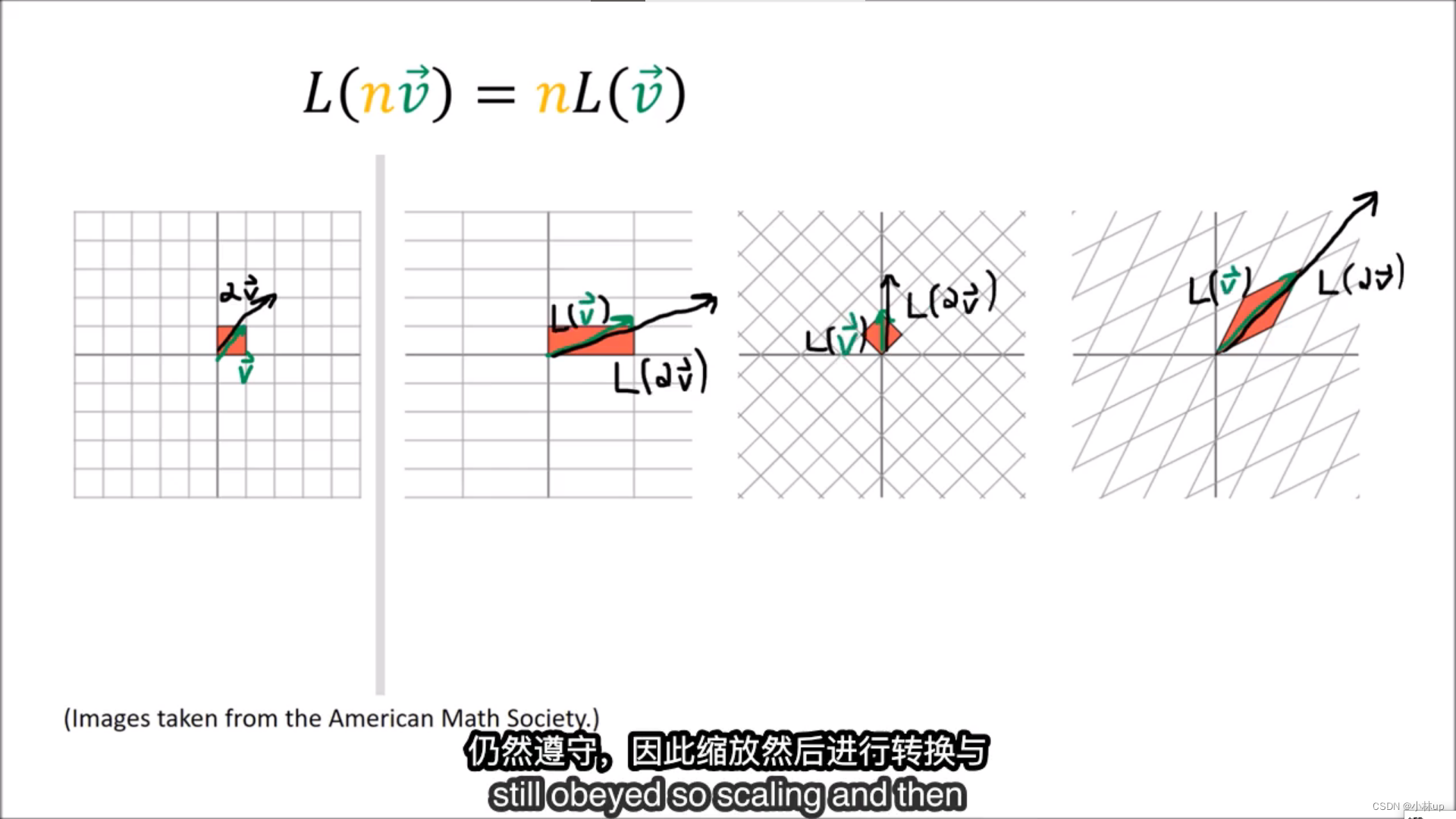


以上两张图片通过代数运算给出了线性映射(矩阵)的计算规则。
探究:在不同基下的坐标进行线性变换
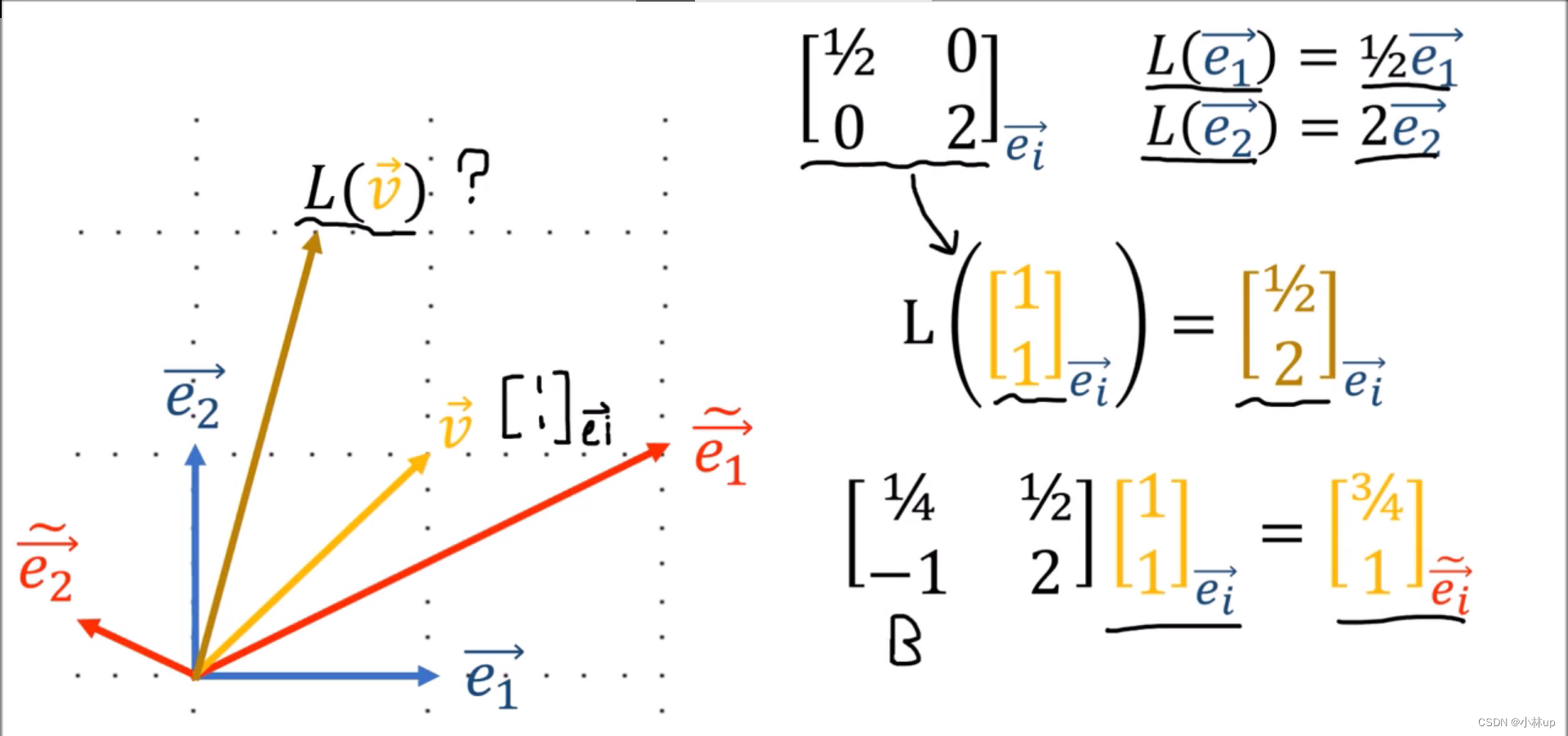
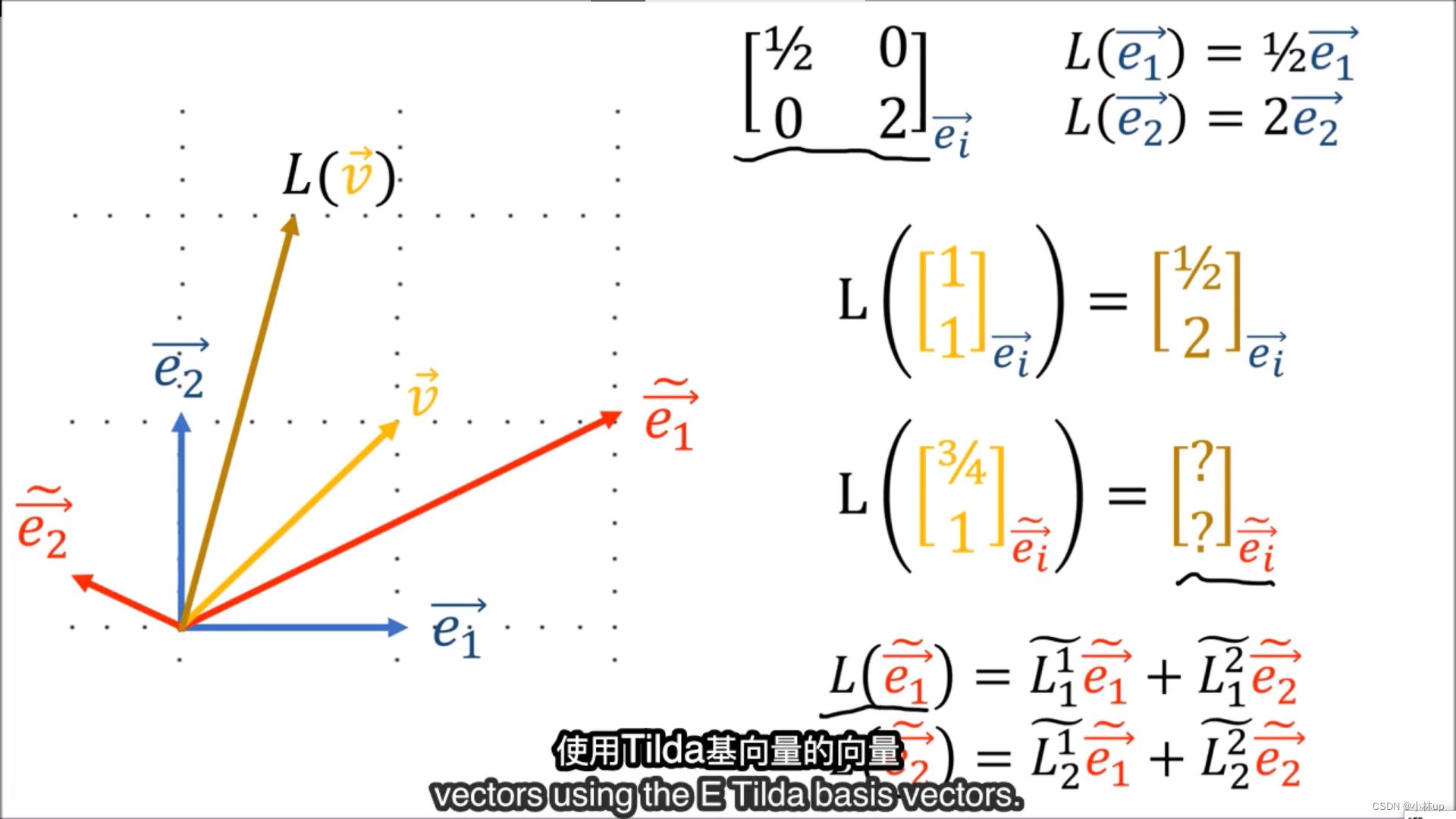
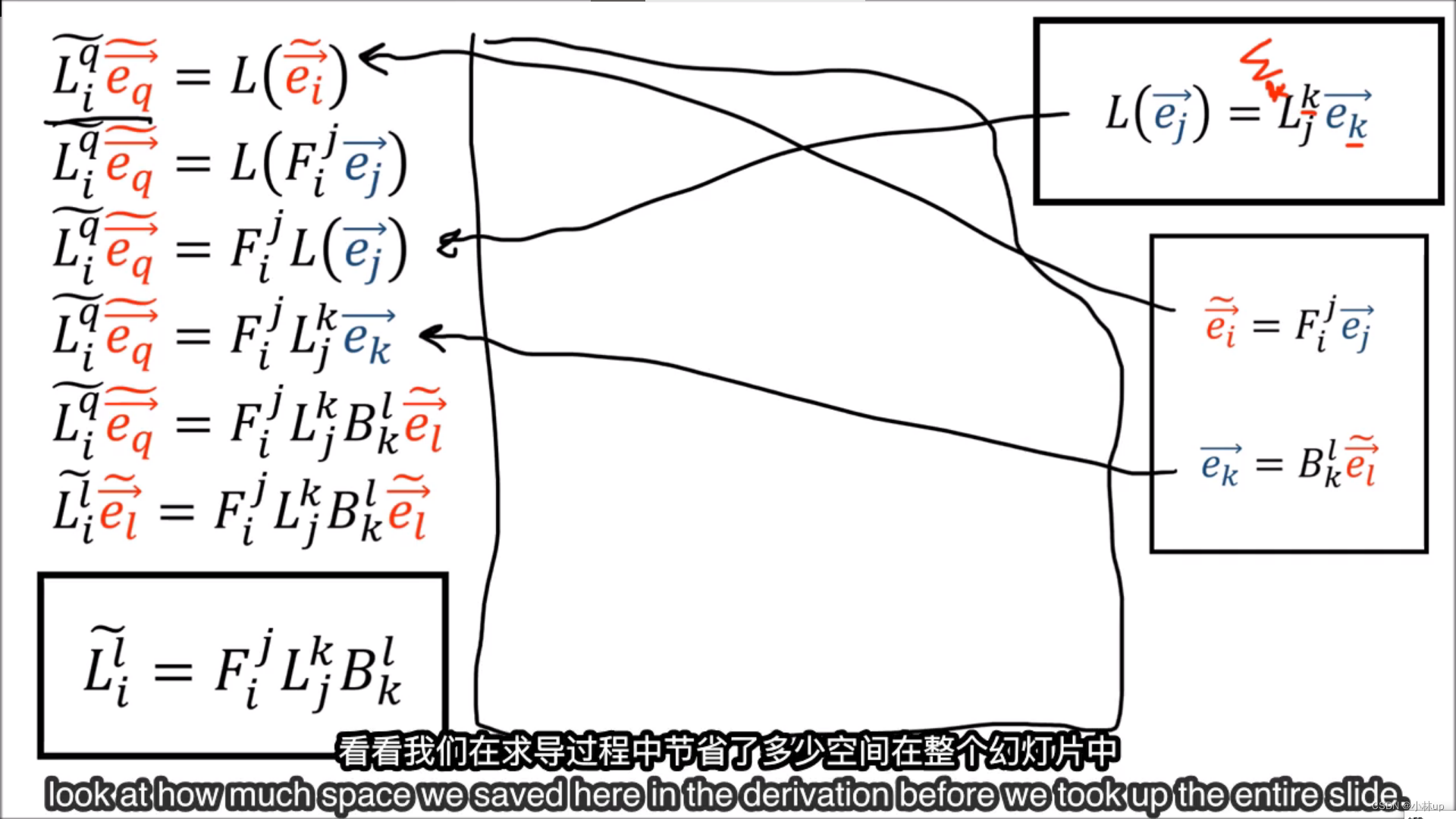
我们不能再使用原来的基下的变换矩阵,我们需要求新的基下的变换矩阵。



于是我们的问题就可以解决了。
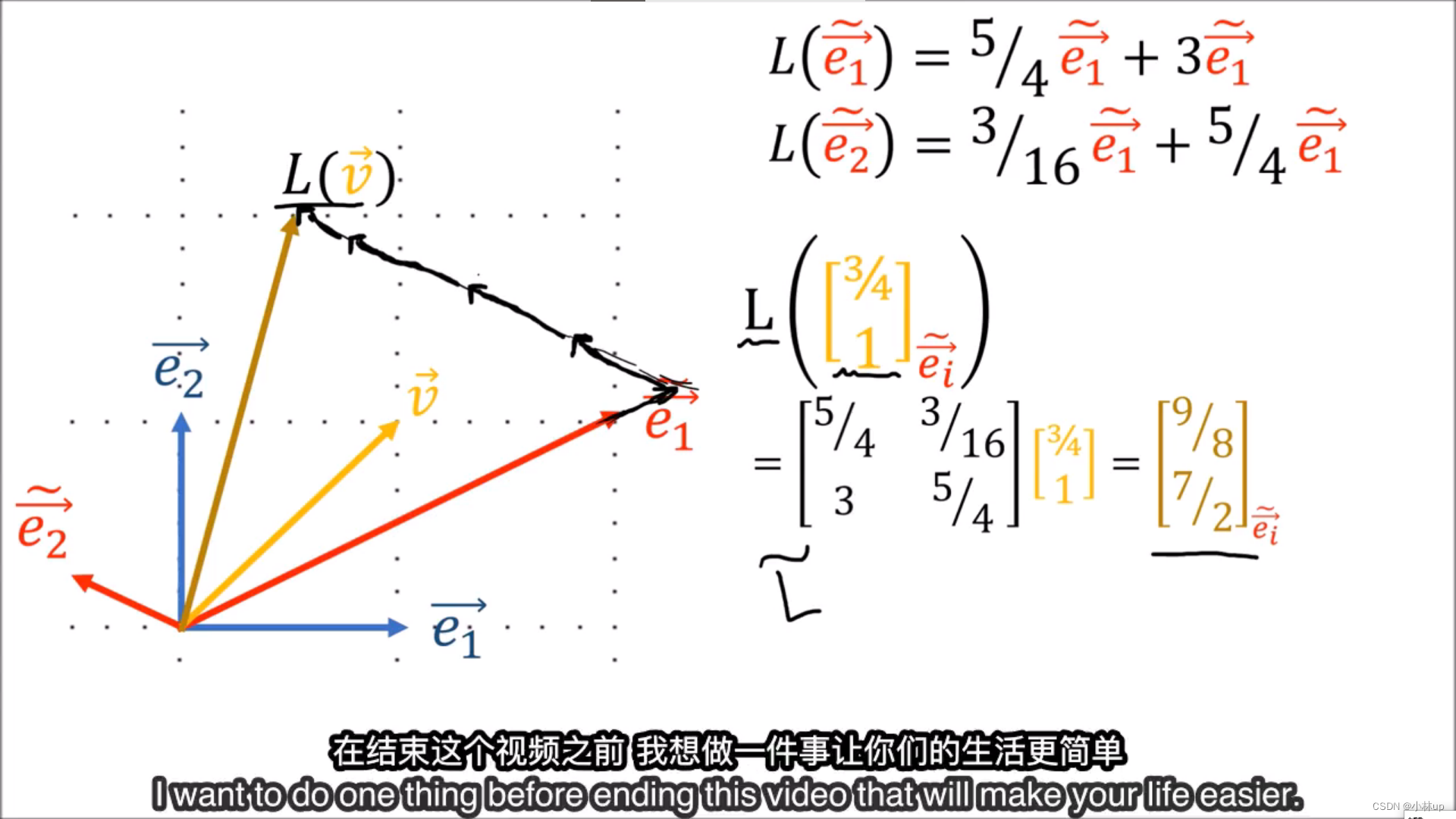
然后就引入了爱因斯坦求和法则:
矩阵乘一个单位阵还是自己用张量表示:

我们还可以得到线性变换反向转换的表达式:
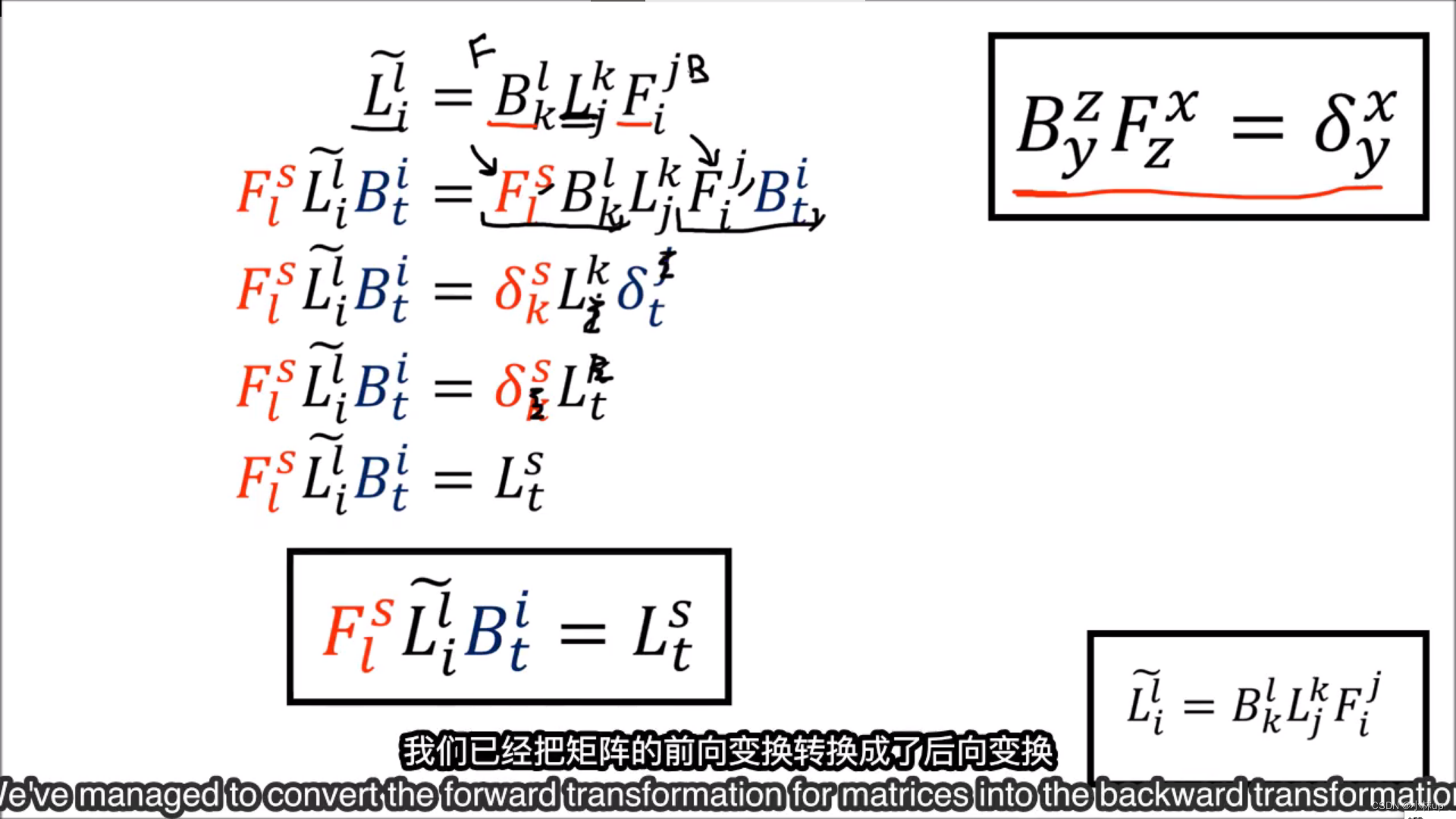
那么现在我们就学了:

6. 度规张量 The Metric Tensor



于是这样就引出了度规张量(线性代数的二次型派上了用场)

举个例子:

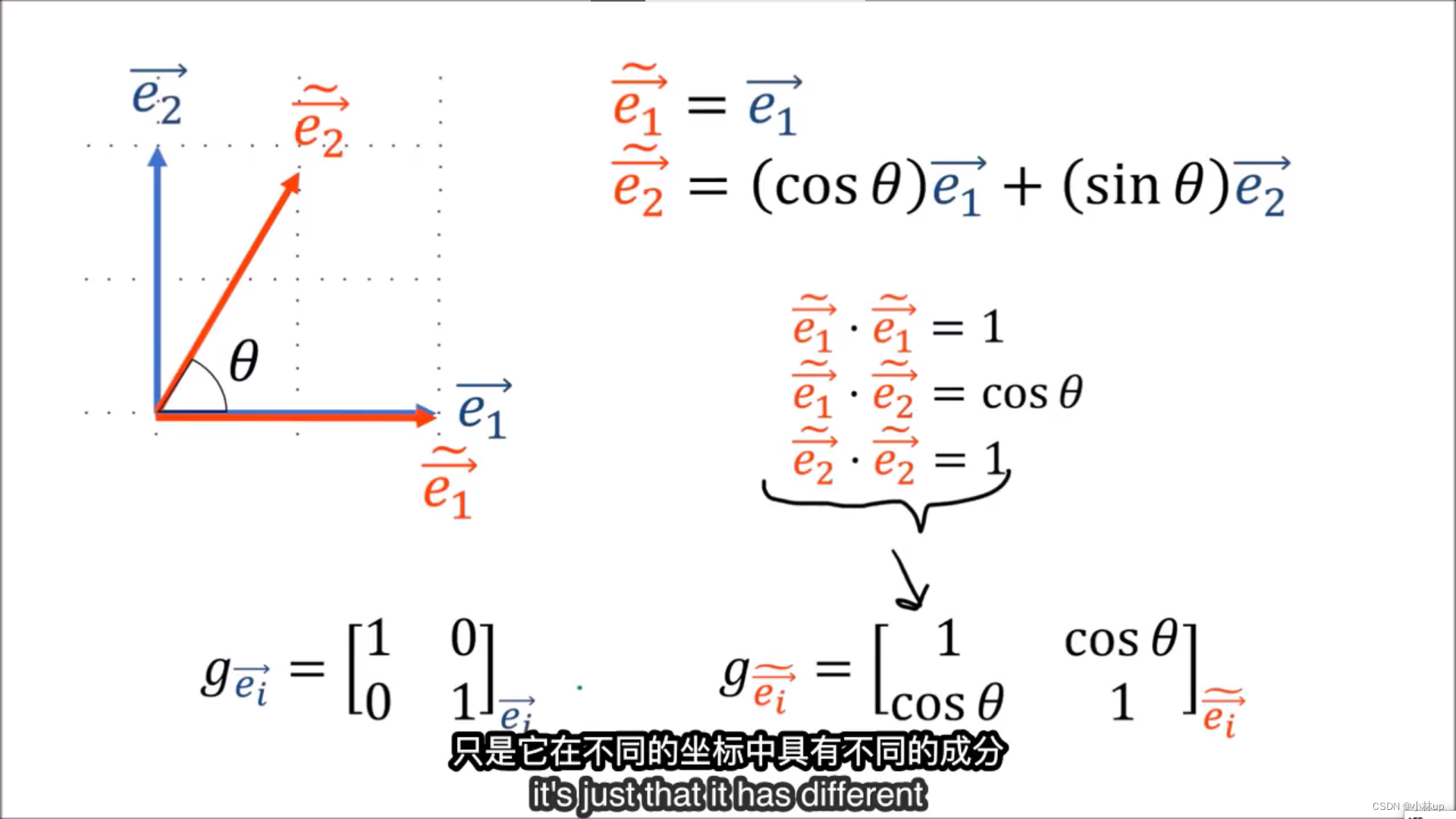
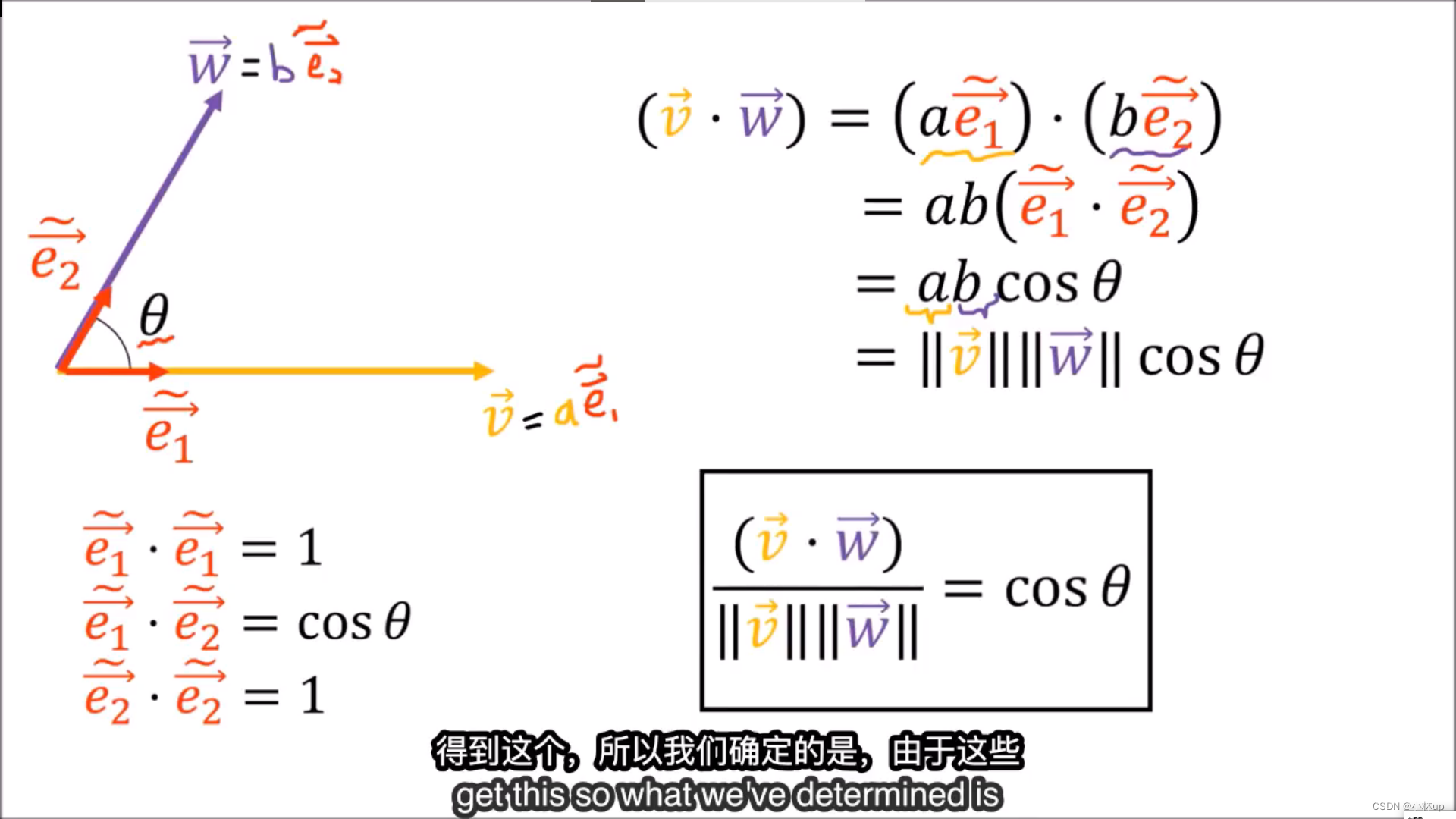
于是长度我们可以计算,角度我们也可以计算。




目前学到的张量。




对于度规张量的数乘。
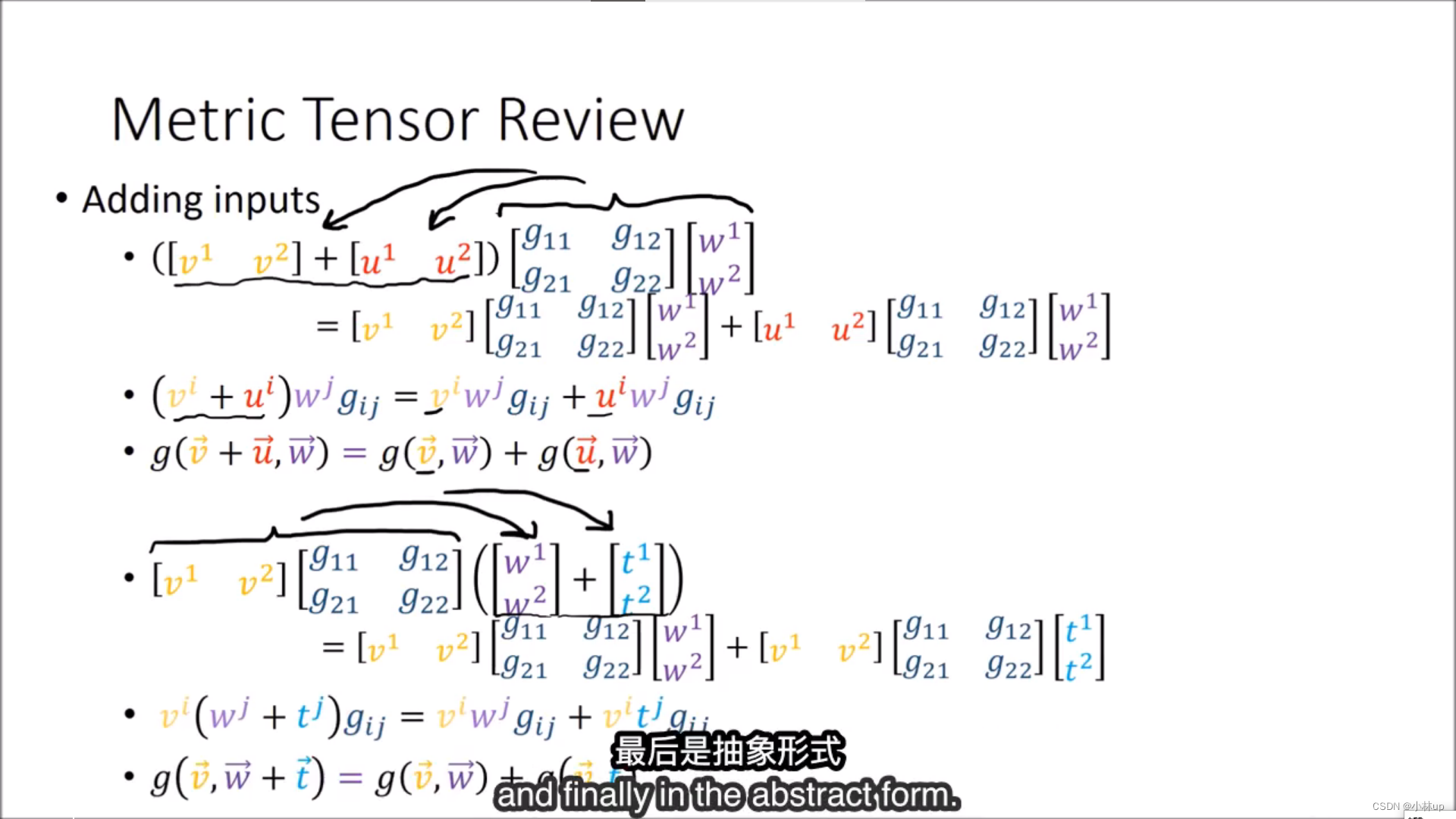

对于度规张量的加法。

于是(0-2)型张量引出了二次型。
二次型有双线性,可以类比与余向量。
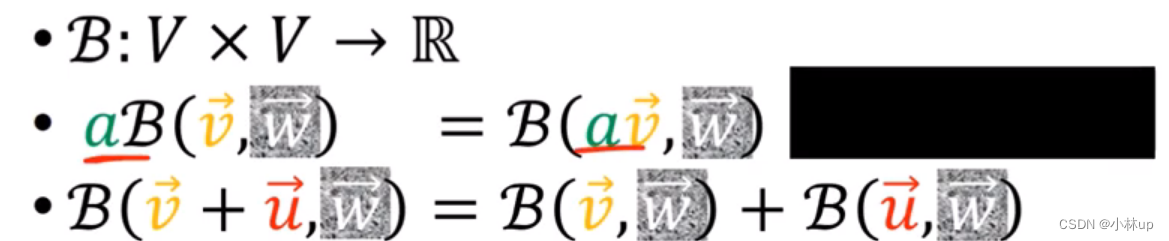
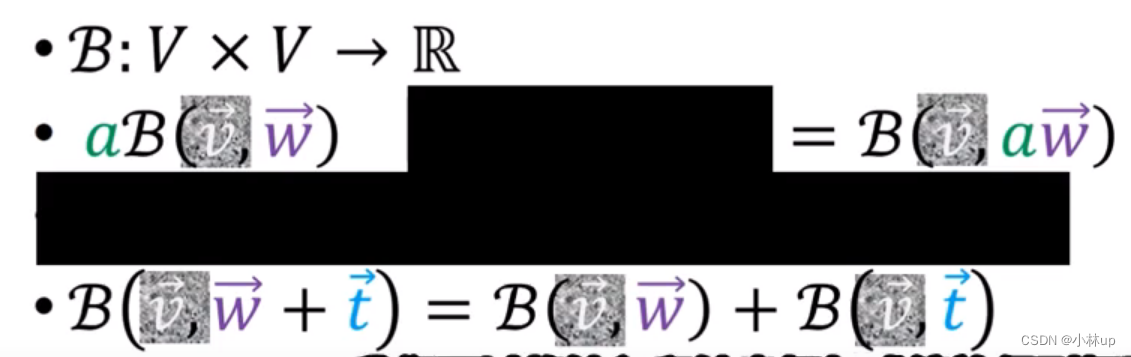
这里的双线性指的是一个输入线性变化时,另一个输入保持不变。

对于(0-2)型tensor还有以上的两个性质。
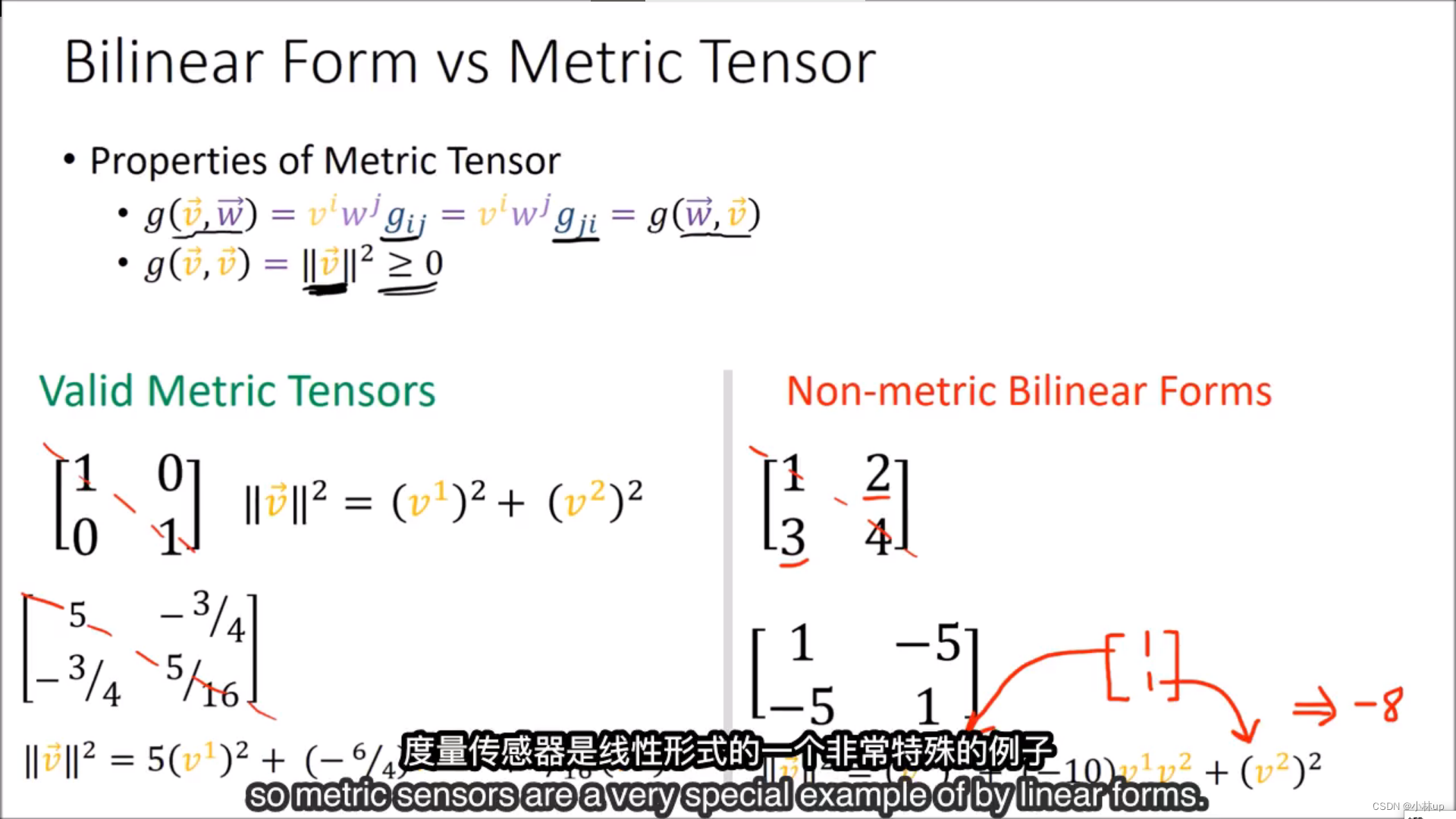
不是所有的度规形式都是张量,需要满足上一张图的两个性质。
7. 张量积 Tensor Product
先复习一下我们之前学到的张量:

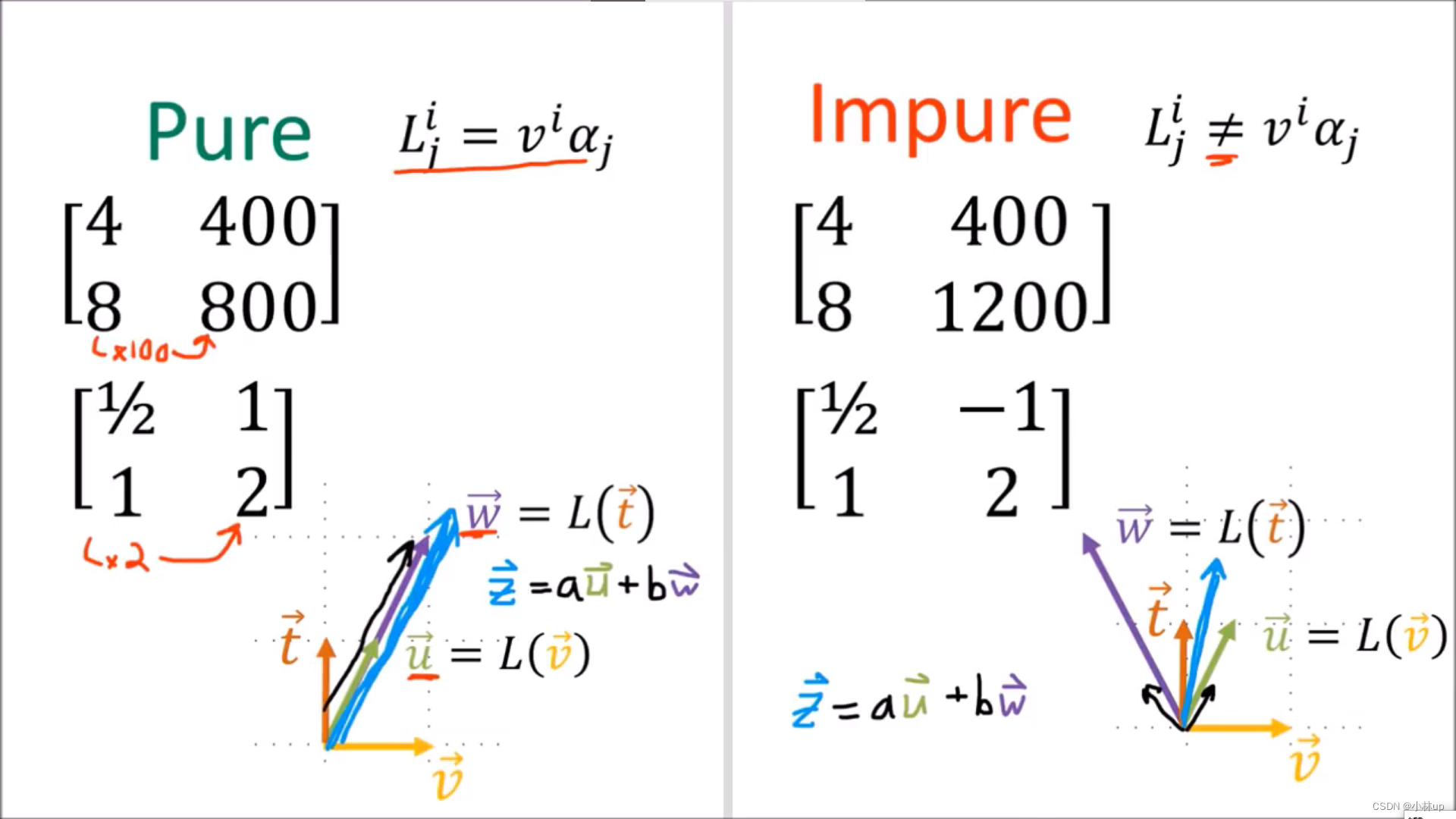
一个矩阵(线性映射)如果可以分解为一个列向量(向量)和一个行向量(余向量)相乘,称它是pure的。否则是impure的。

使用标准基和对偶基我们可以构造四个基本矩阵。

所有的
2
×
2
2\times 2
2×2的矩阵都可以写作是这四个基本矩阵的线性组合。我们称这四个矩阵是KaTeX parse error: Undefined control sequence: \time at position 2: 2\̲t̲i̲m̲e̲ ̲2型矩阵(线性映射)的基。

对于线性映射我们可以重新书写一下。如上所示,得到线性映射后的元素的计算的方式。

当然线性映射也可以选择其他的基。

我们可以对pure Linear Map和Impure Linear Map重新总结一下。接下来我们就可以引入张量的记号了。



为了简化对于张量积的符号还是写作左边的这种形式。
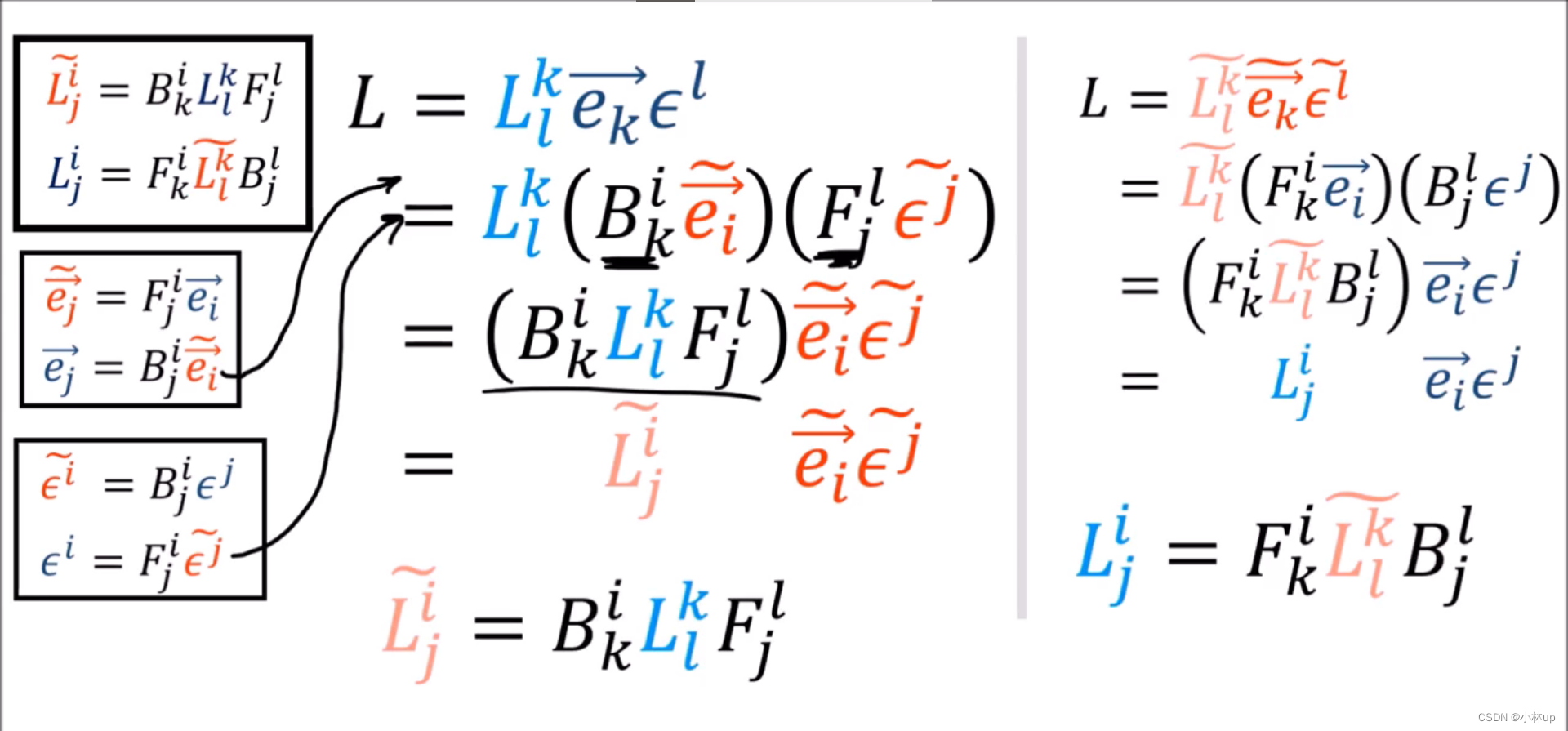

张量积给我们看线性映射带来了新的视角。
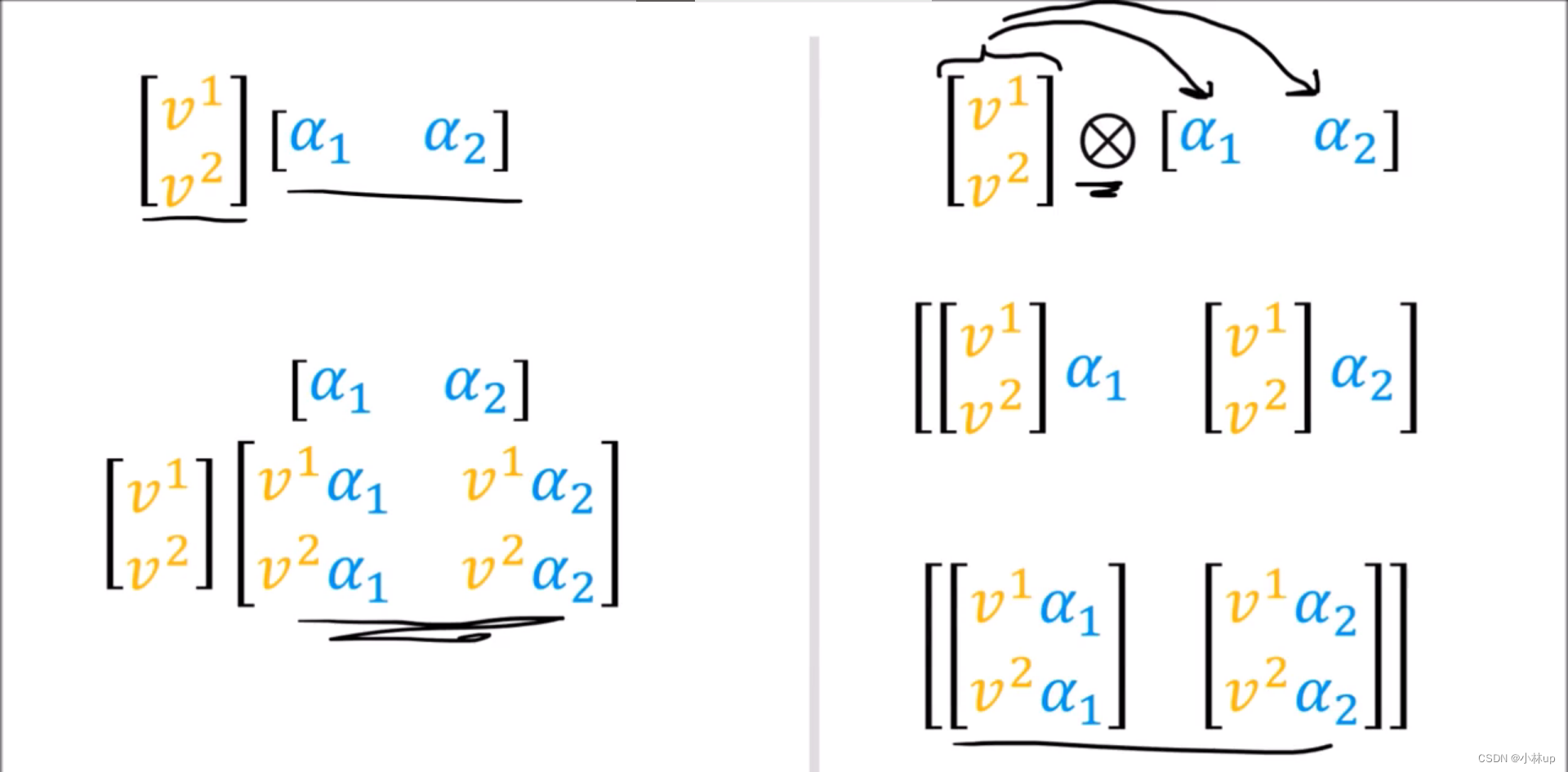
张量积(上图右边的一个直观的表达)。

对于二次型的形式我们也可以看成是两个余向量的形式,为什么呢?余向量需要有一个向量作为输入,这点和二次型需要两个向量输入很相似。
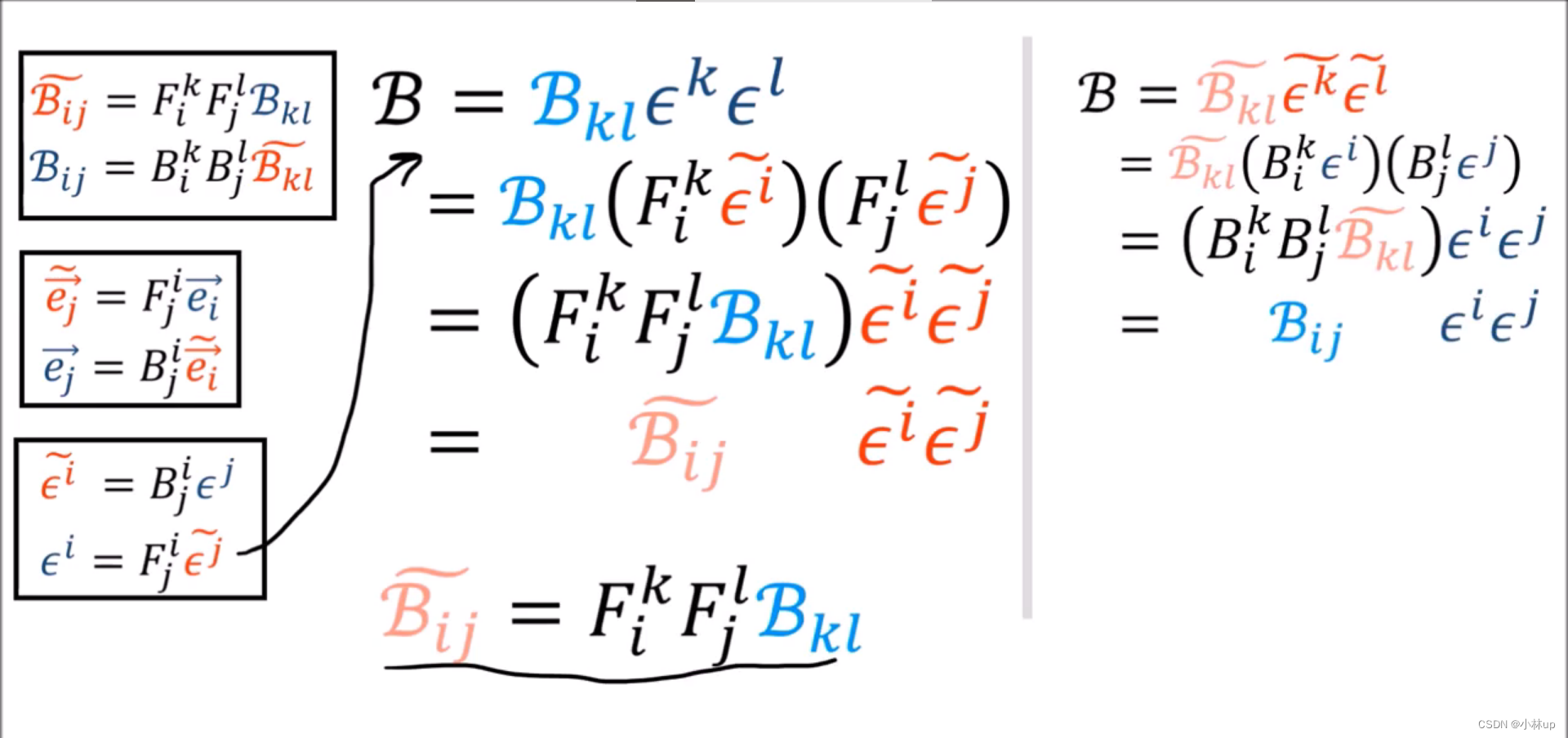
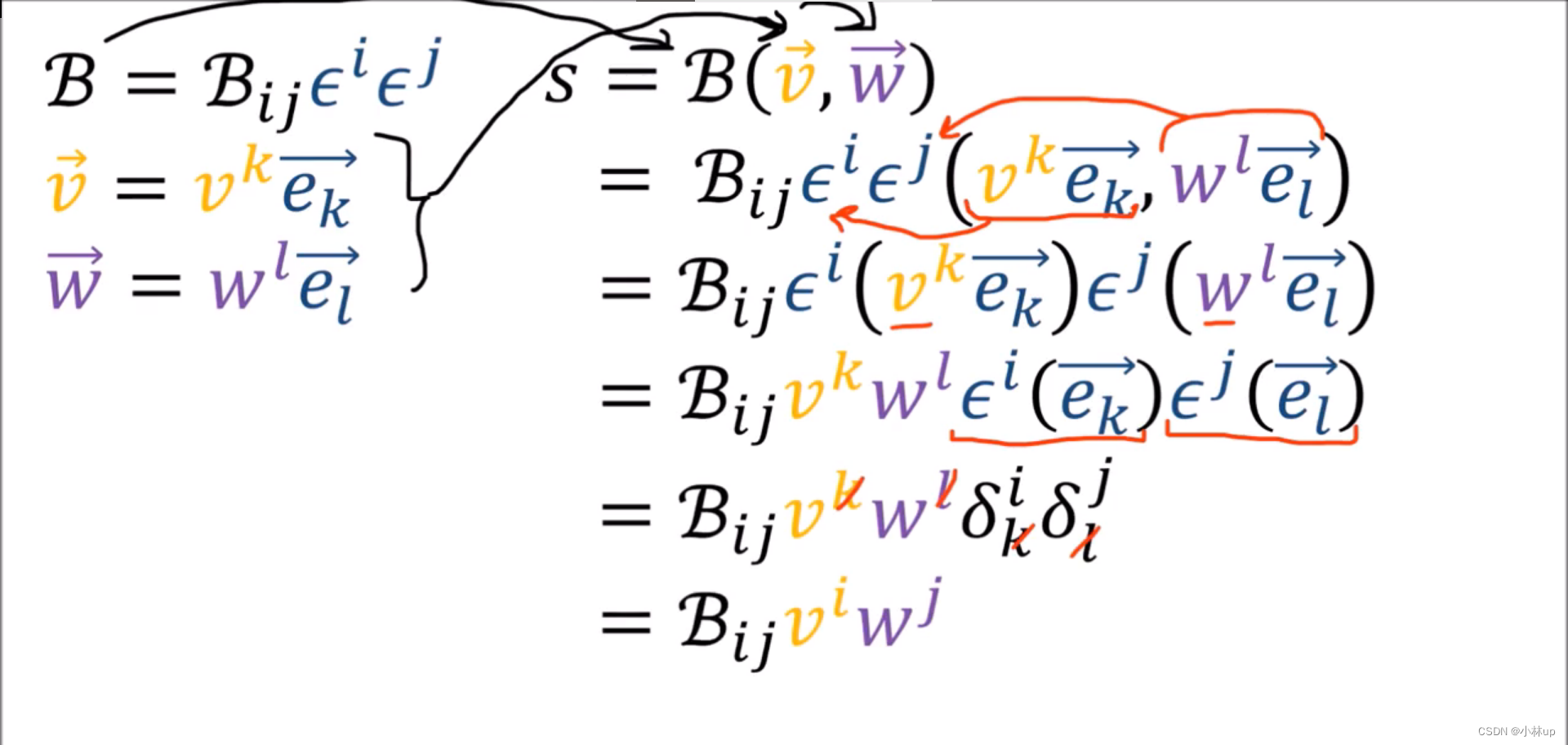
张量积给我们看二次型带来了新的视角。
好像使用张量积表示二次型不太对?

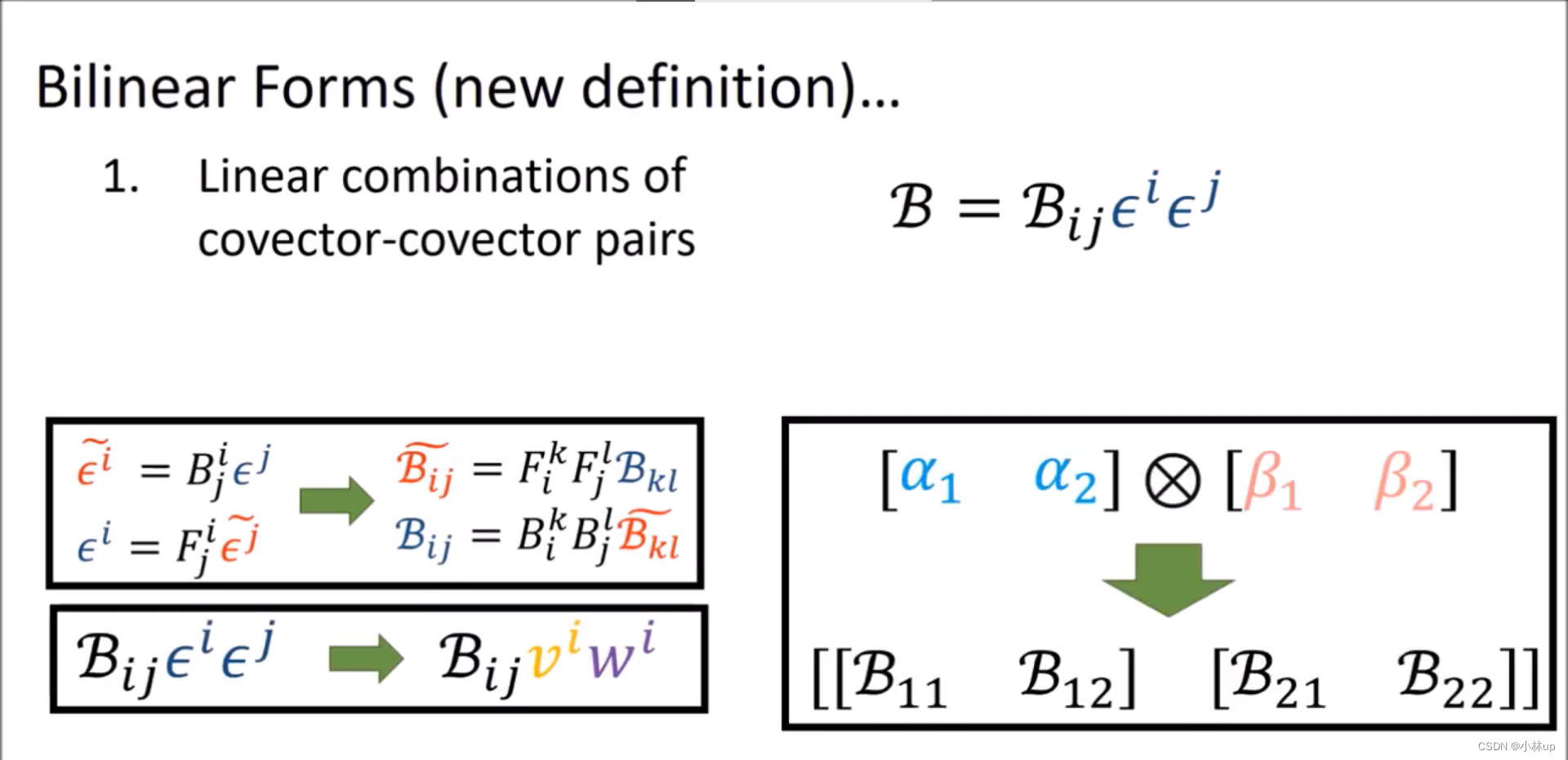
看上面的图我们呢知道只是形式不同罢了。
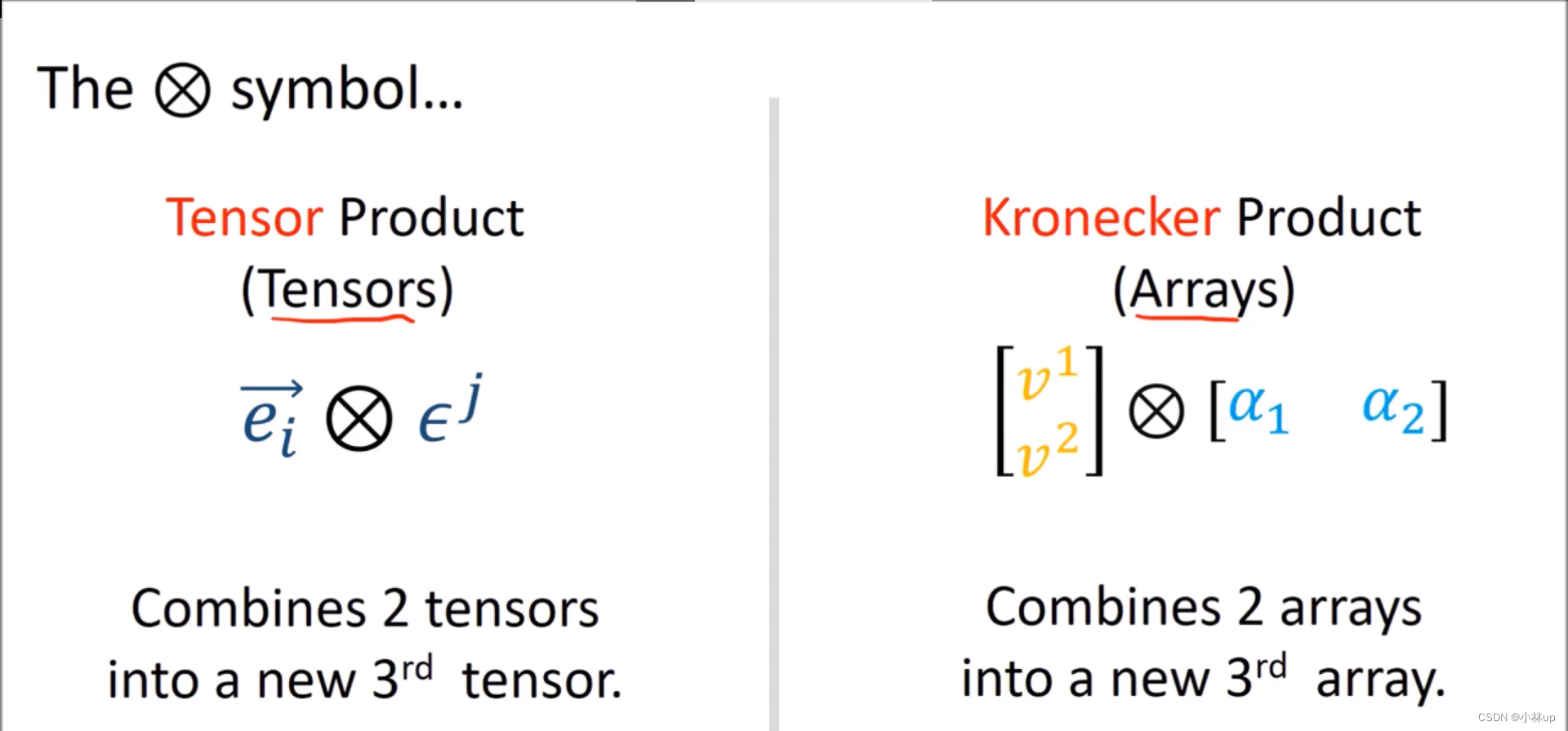
关于
⊗
\otimes
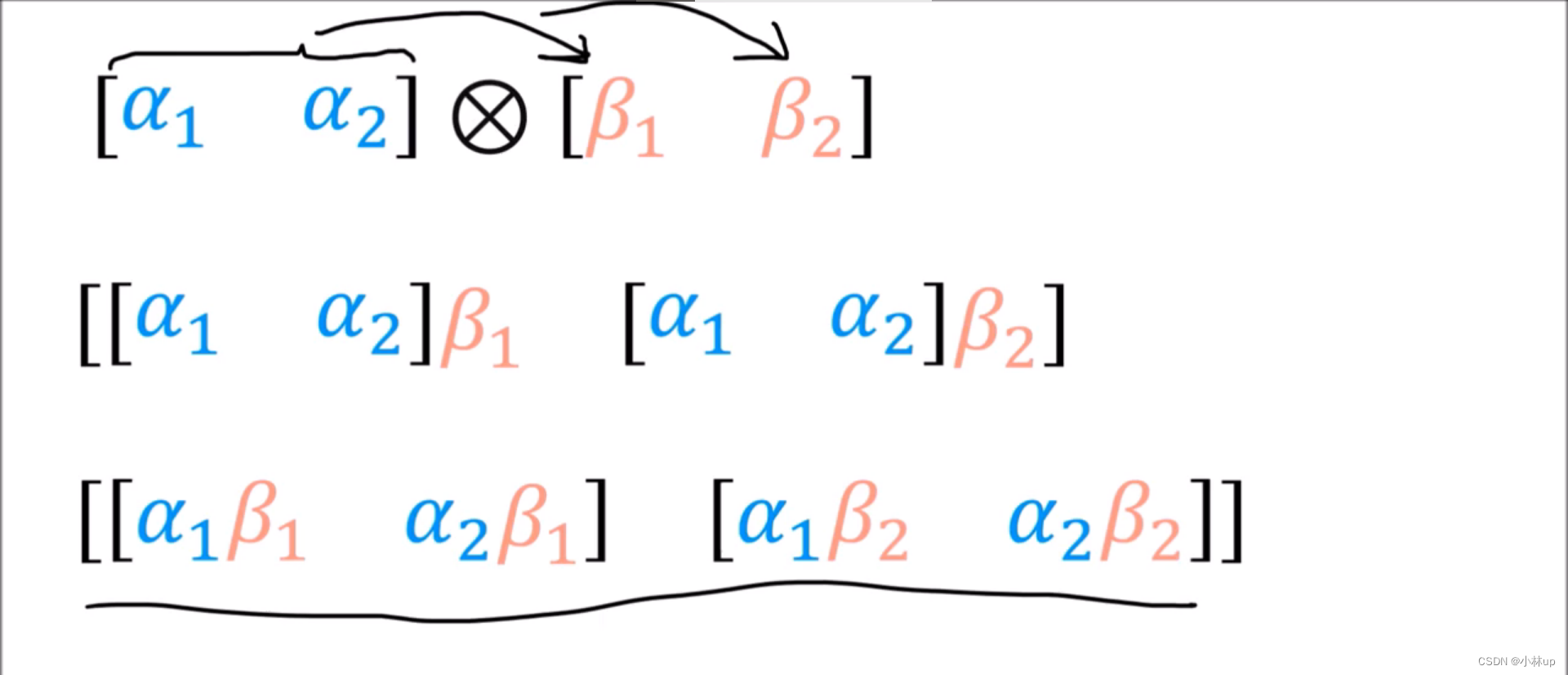
⊗记号,分别可以作用于张量(张量积)和数组(Kronecker积)。

回顾一下标准基和对偶基。

张量积作用两个张量出来还是张量。

使用张量积我们也可以看到线性映射是怎么作用在向量上的。
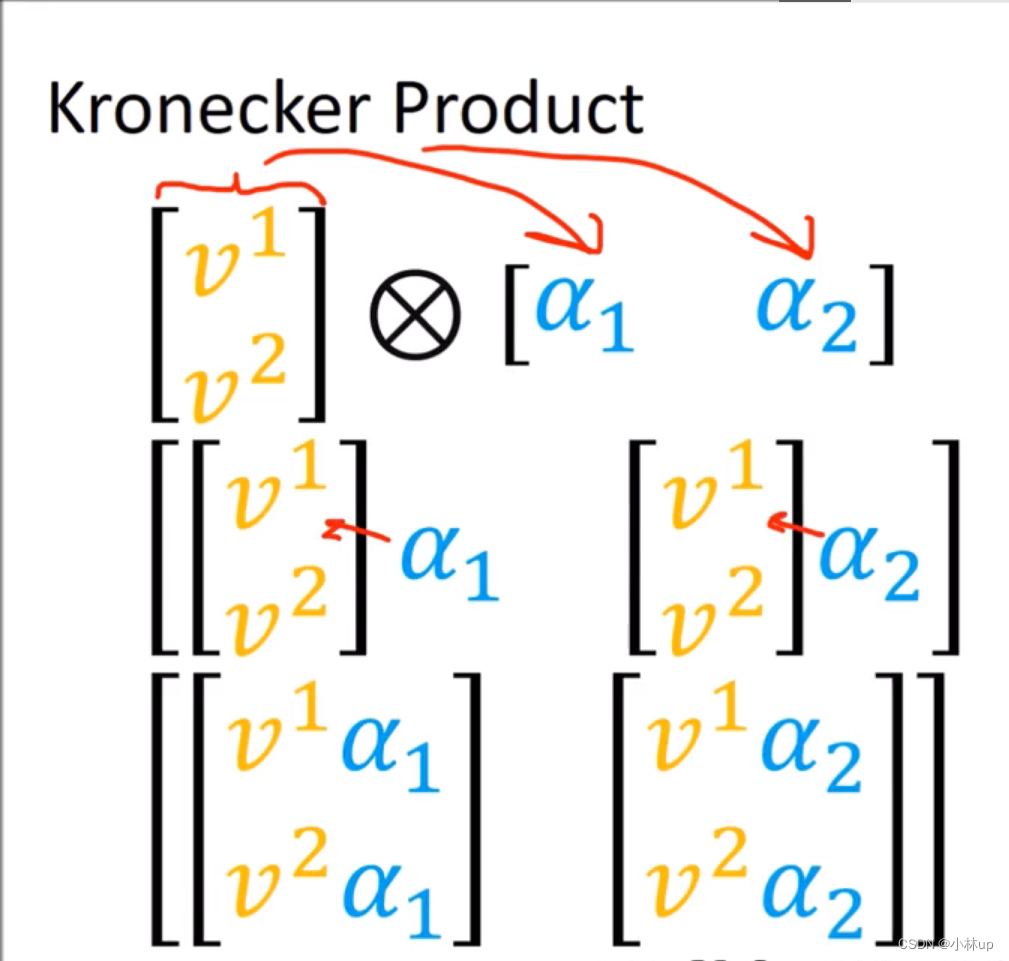
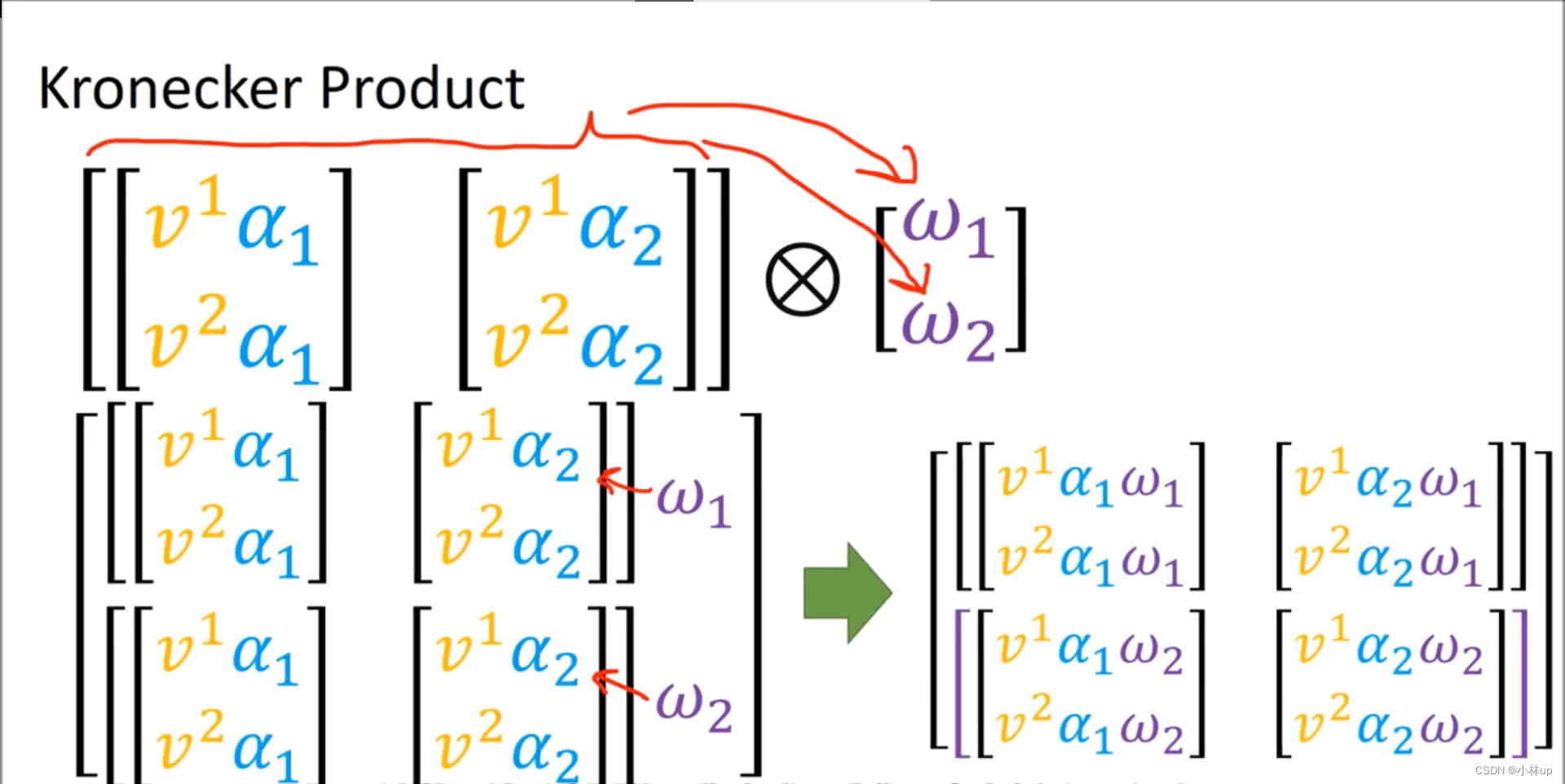
上面两个图是使用Kronecker积作用在向量上。
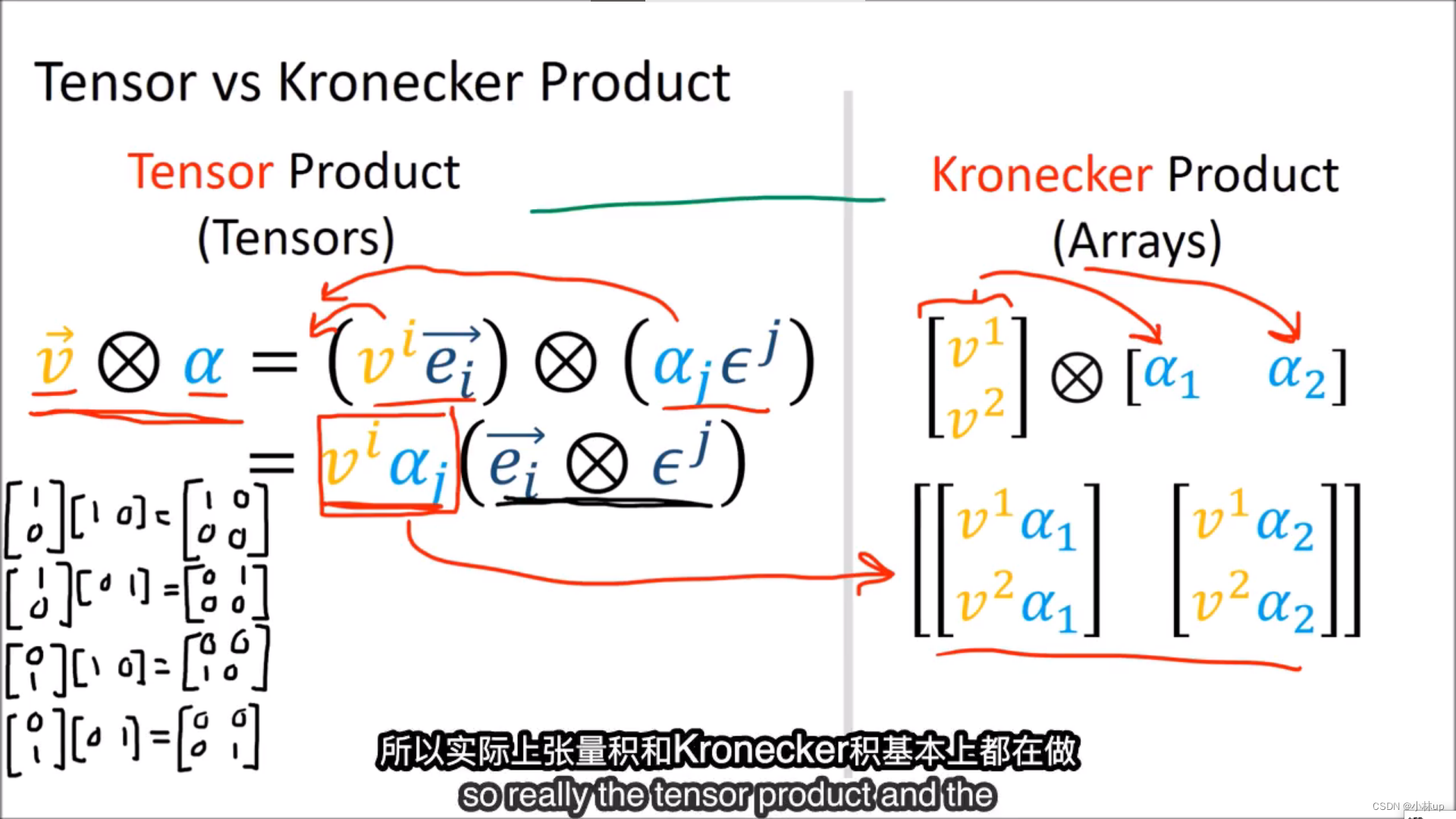
其实两者在做类似的同样的事情,不过张量积将抽象的基也考虑进去了。
如前所述:使用张量积可以很简单地定义线性映射:
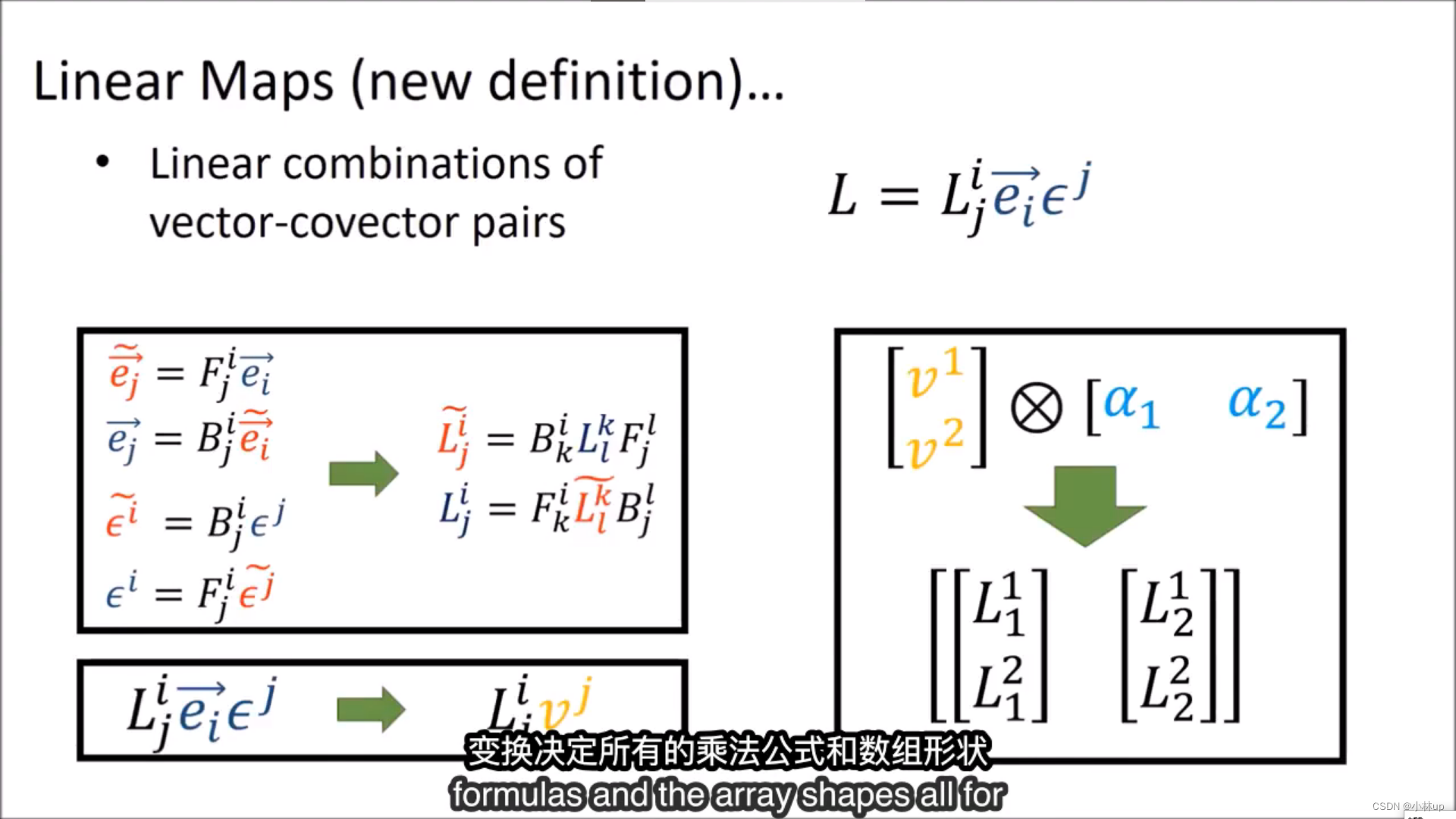
以及二次型。

接下来我们来看一些没见过的张量。

上面的图左边是(2-0)型张量,右边是(1-2)型张量。我们不禁要问:对于新的张量类型我们怎么定义坐标转换的规则?如果要计算
Q
(
D
)
Q(D)
Q(D),乘法公式是什么?以及矩阵的形状是什么样的?

上图解决了第一个问题:新的张量怎么进行不同的坐标转换?

上图解决了第二个问题:如果要计算
Q
(
D
)
Q(D)
Q(D),乘法公式是什么?答案是不唯一的,你有各种各样的组合方式。这样写写不清楚,我们还是需要按照爱因斯坦的求和法写出分量的表达式。
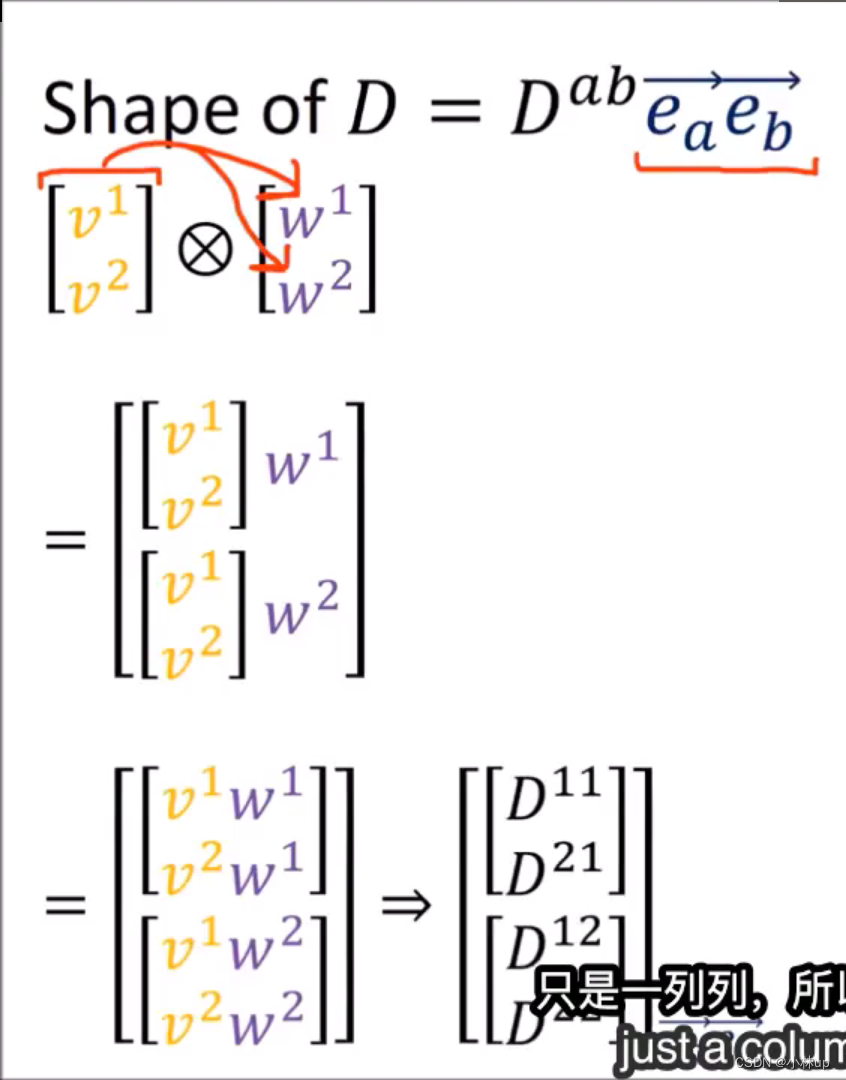
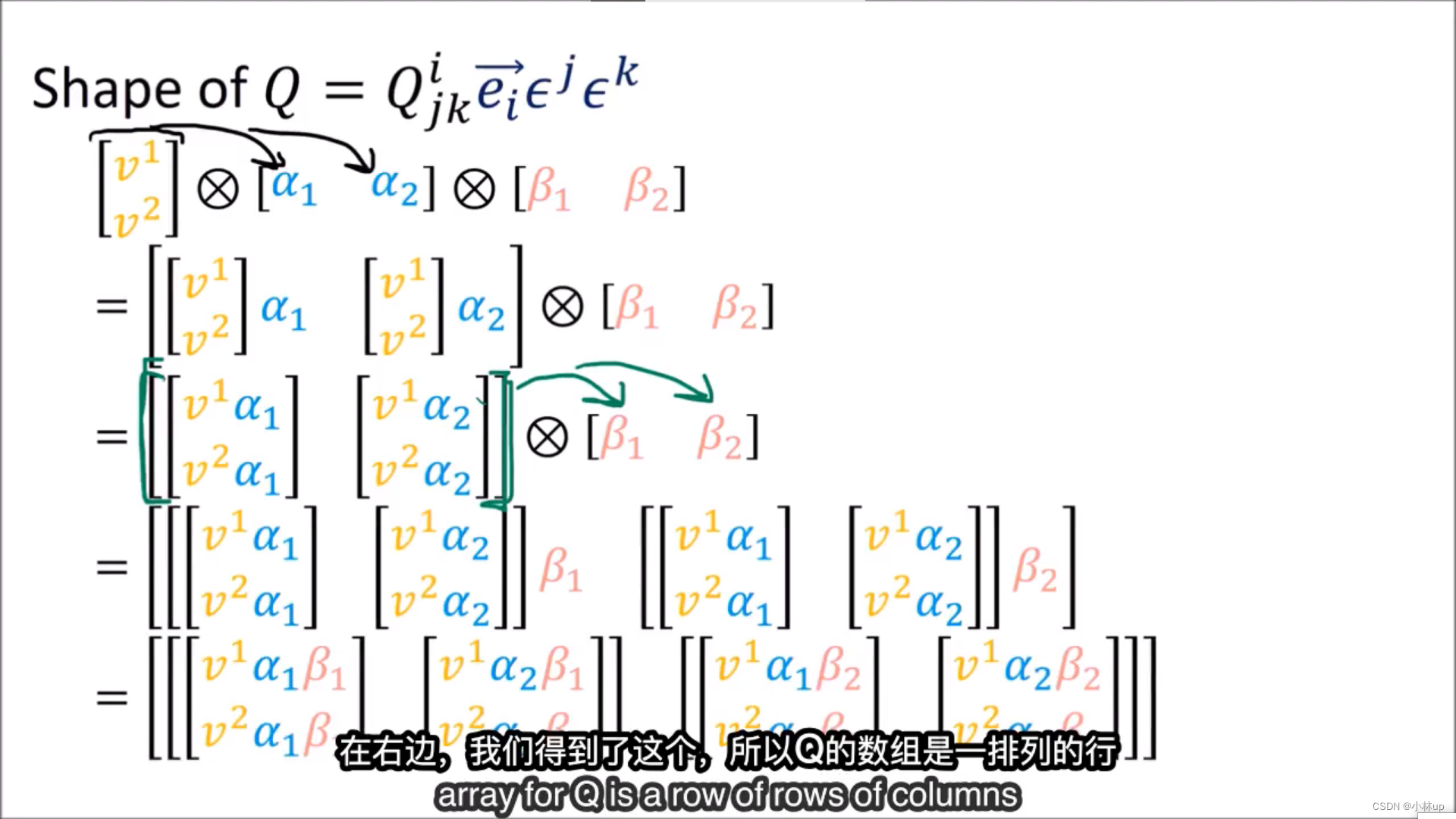
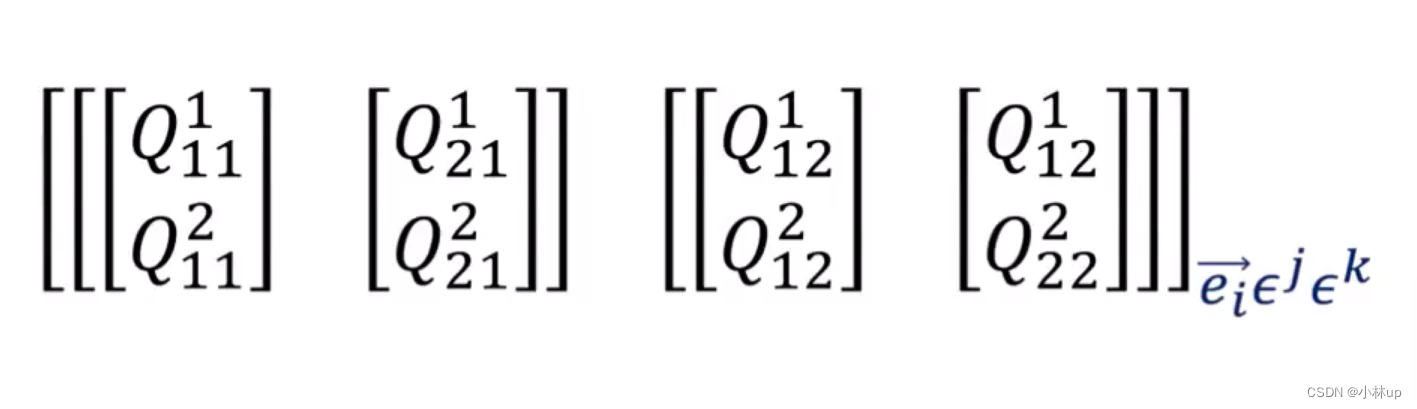
对于张量
D
D
D和张量
Q
Q
Q的表达形式如上图所示。其中
Q
Q
Q是一个三阶张量,可以有上面最后一图的表达方式。


矩阵的乘法在低维的张量很有用,但是在高维的情况下如前所述我们有很多种表达的形式,这是后再使用矩阵的乘法就不是特别好了。我们还是用爱因斯坦乘法来表示我们想要的张量乘法,不然容易发生混淆。
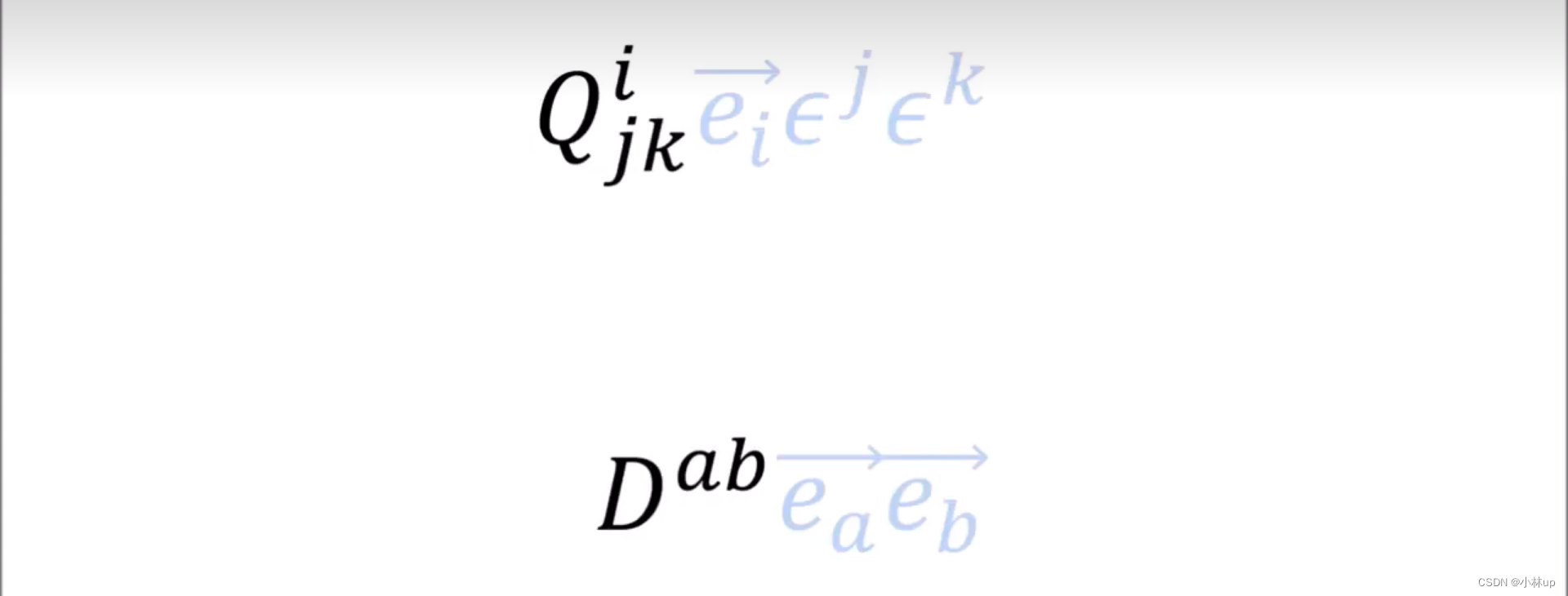
在很多情况下,我们只关注张量的分量。
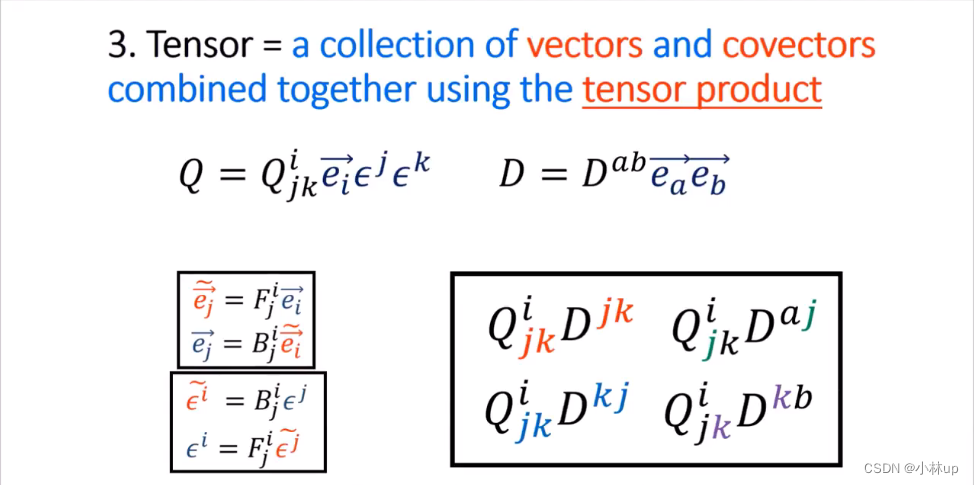
现在我们再次回顾张量的乘定义,应该就很清楚了。
8. 张量积空间 Tensor Product Space
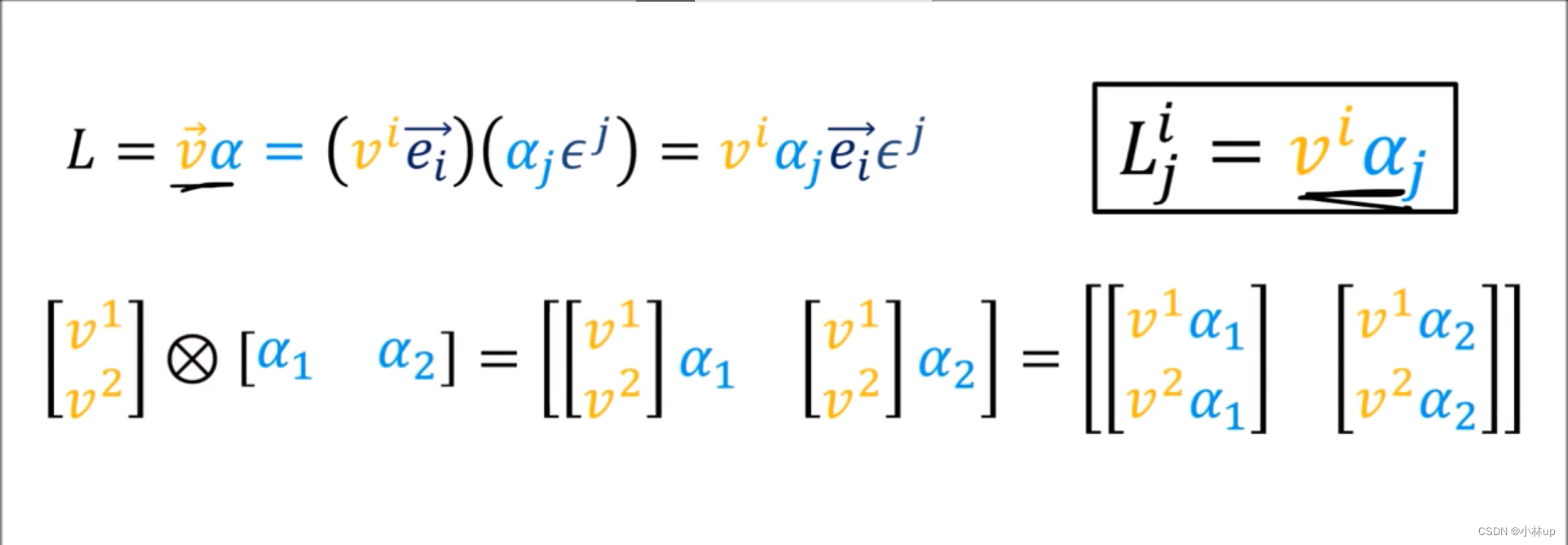
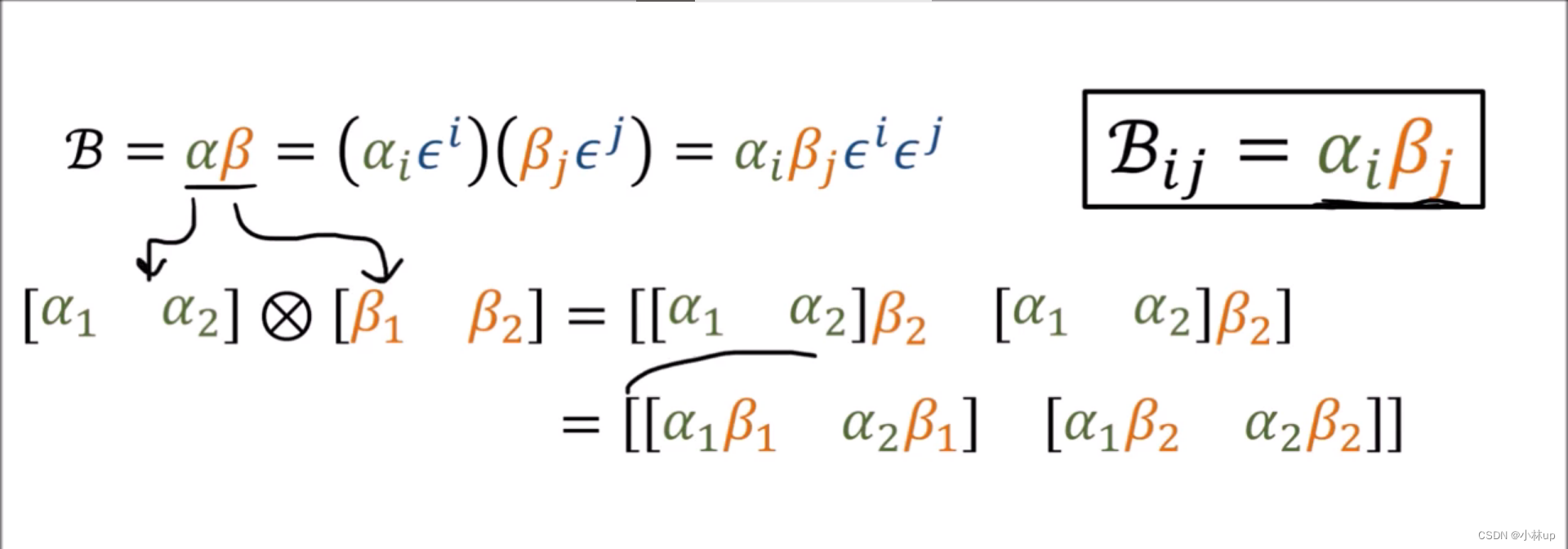
回顾:前面线性映射和二次型的例子
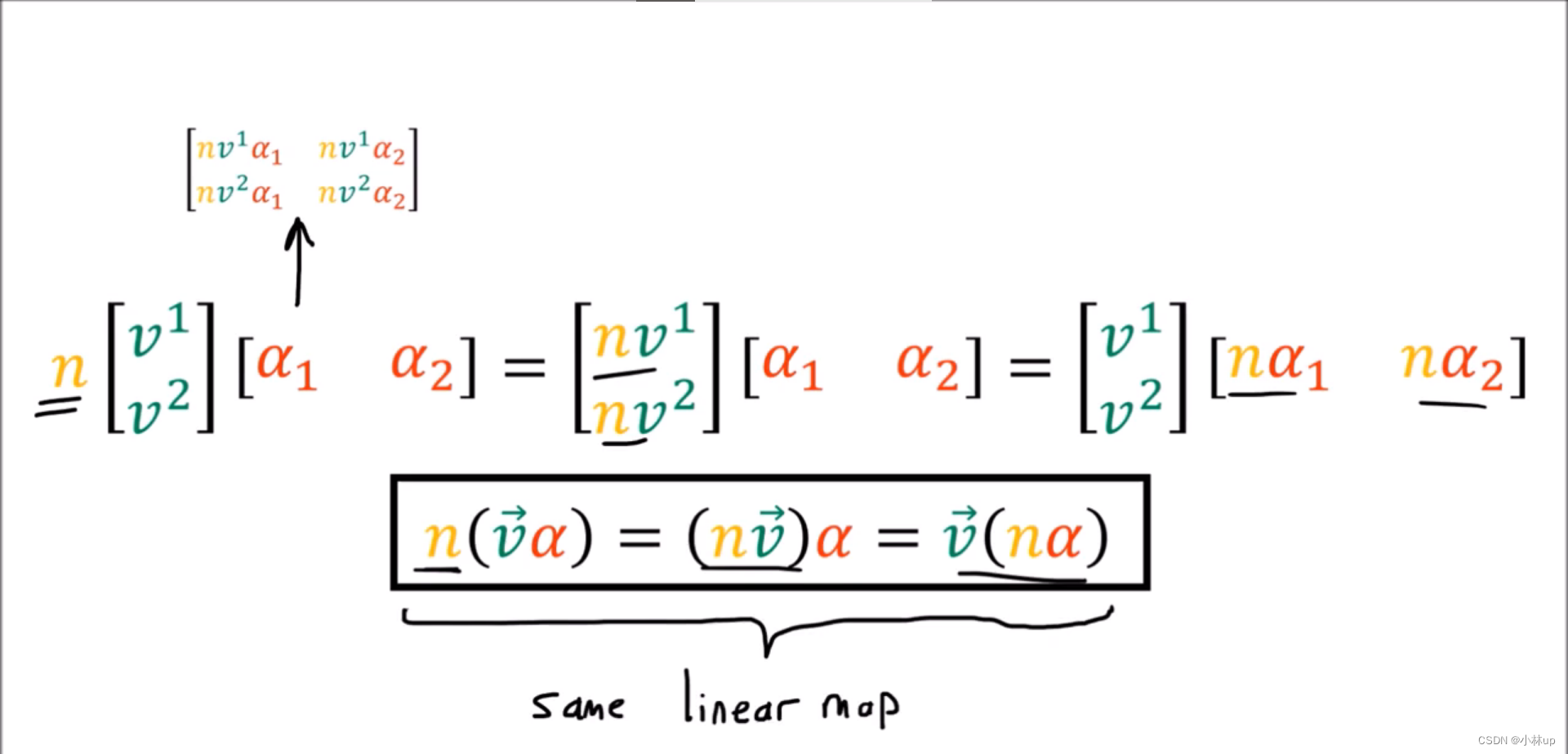
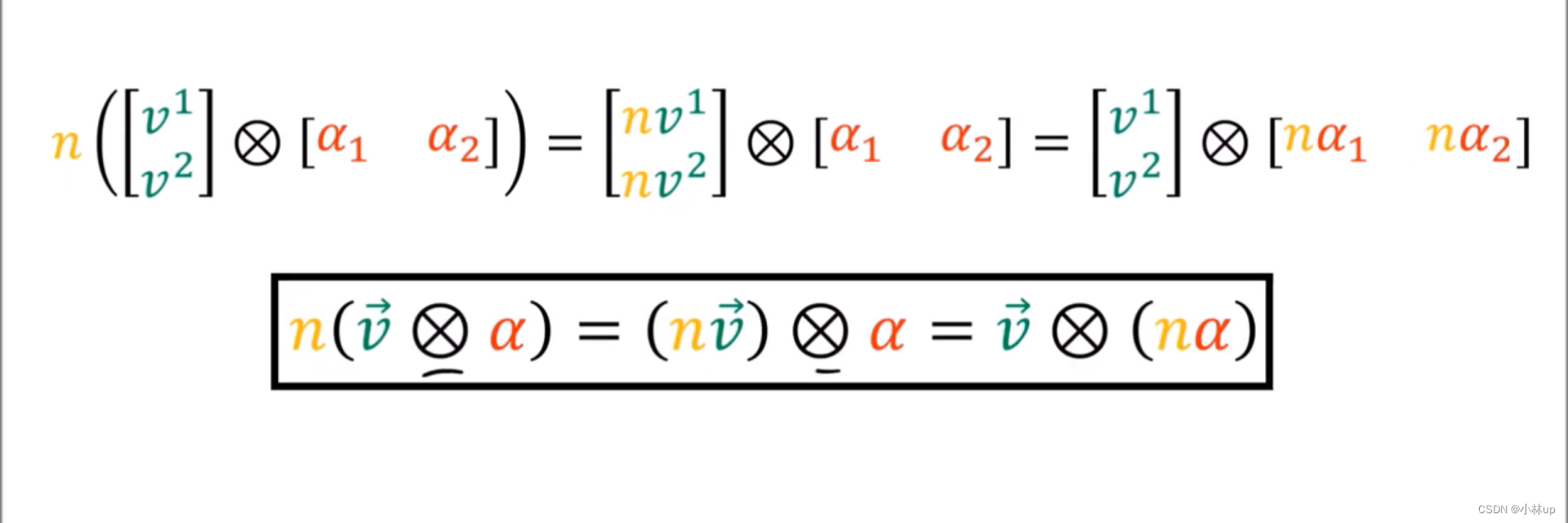
数乘(张量积和Kronecker积是类似的)


加法(张量积和Kronecker积是类似的)
总结一下我们有:
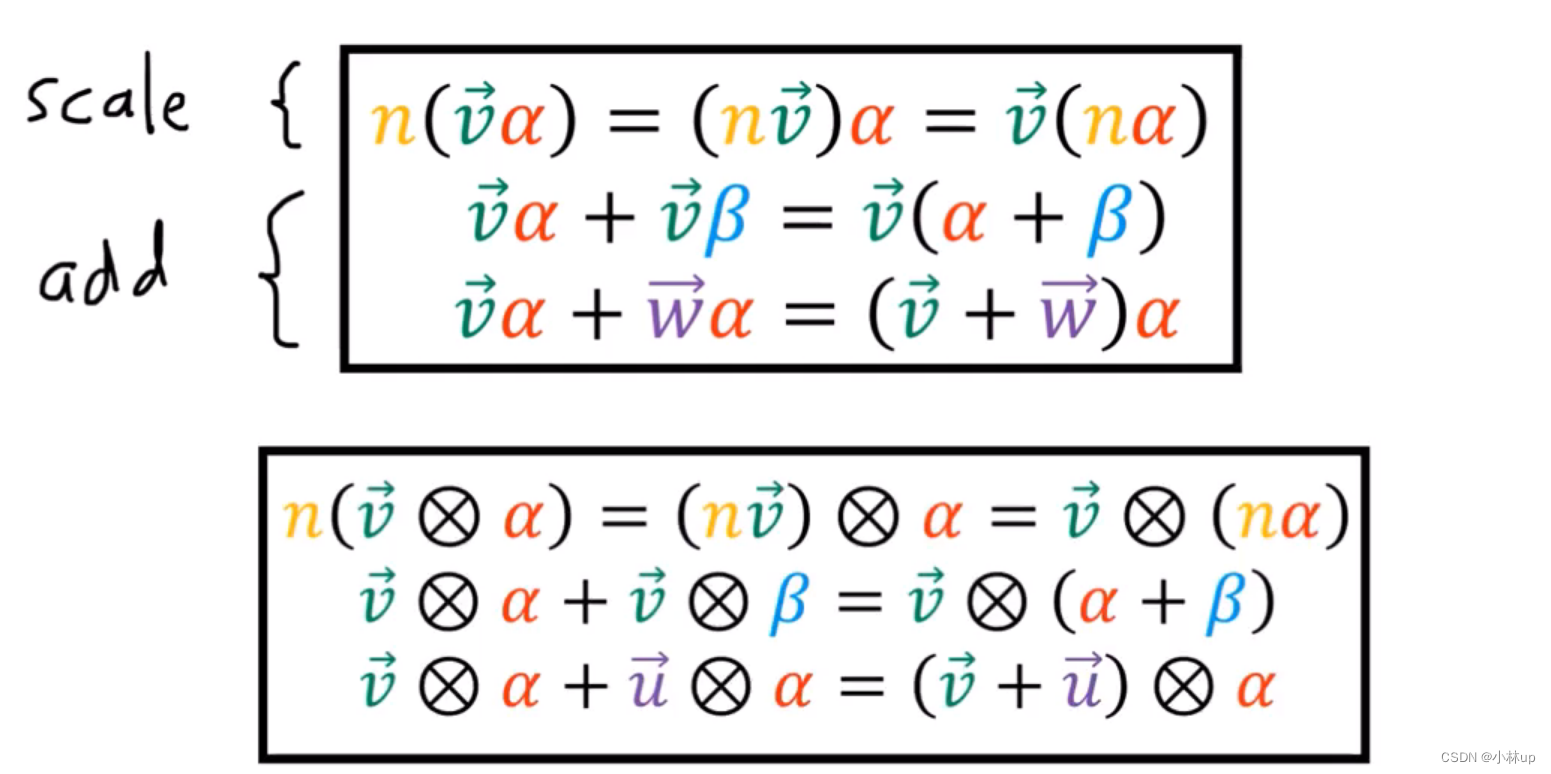


这在计算中很有用(参见上面两图)。
 张量积定义的张量积空间(上图的最后一行)
张量积定义的张量积空间(上图的最后一行)

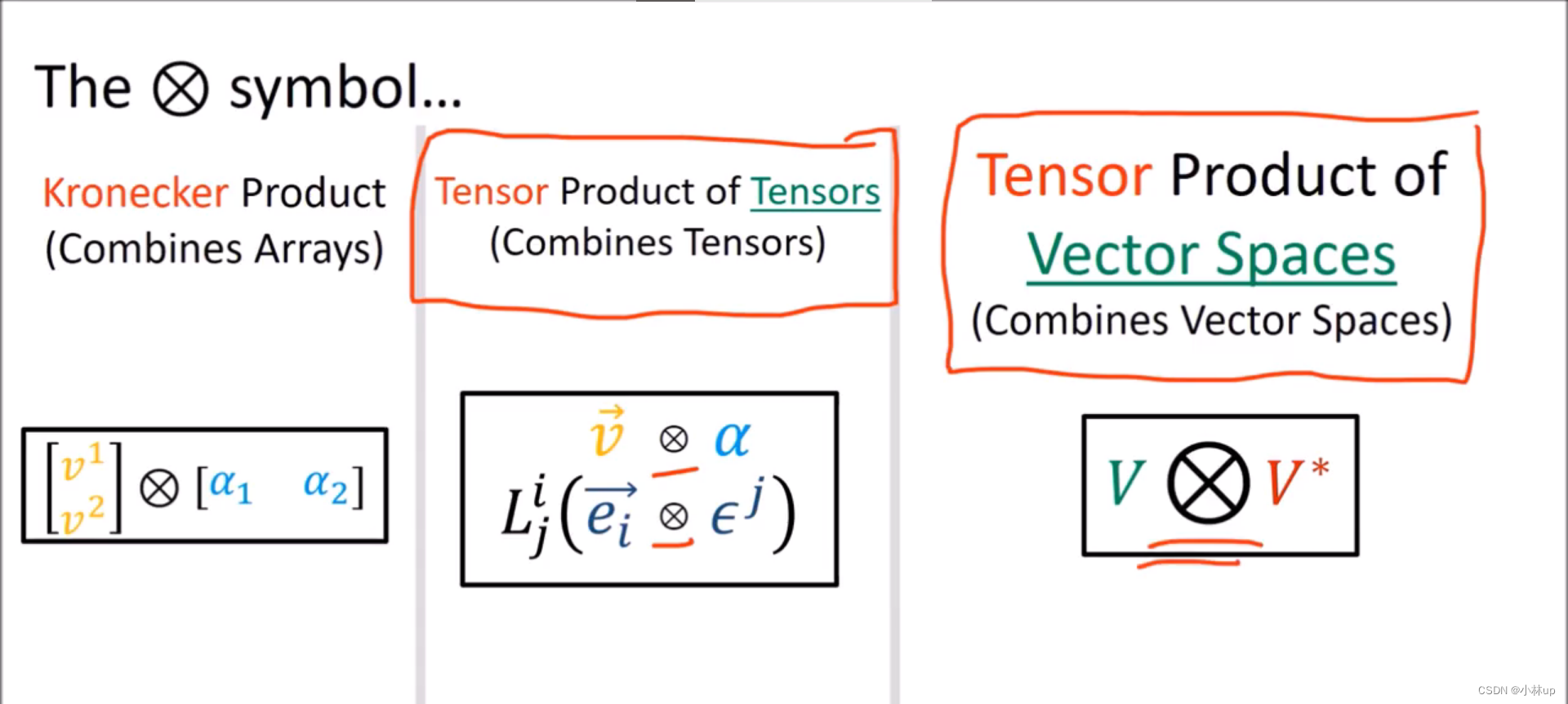
V
⊗
V
∗
V\otimes V^*
V⊗V∗的元素是什么?
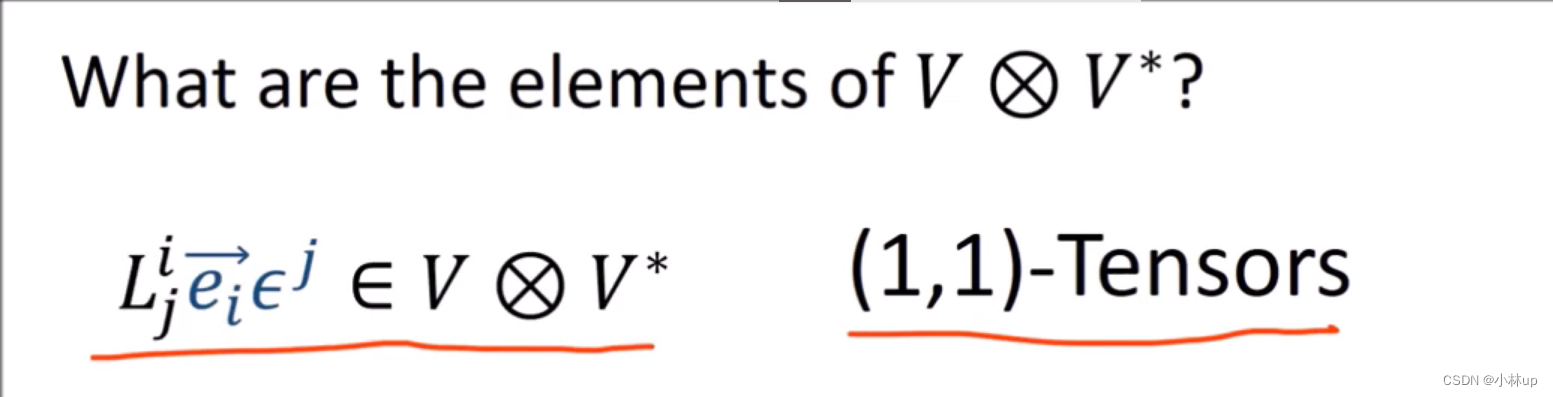
上图说明:
V
⊗
V
∗
V\otimes V^*
V⊗V∗的元素是(1,1)型的张量。
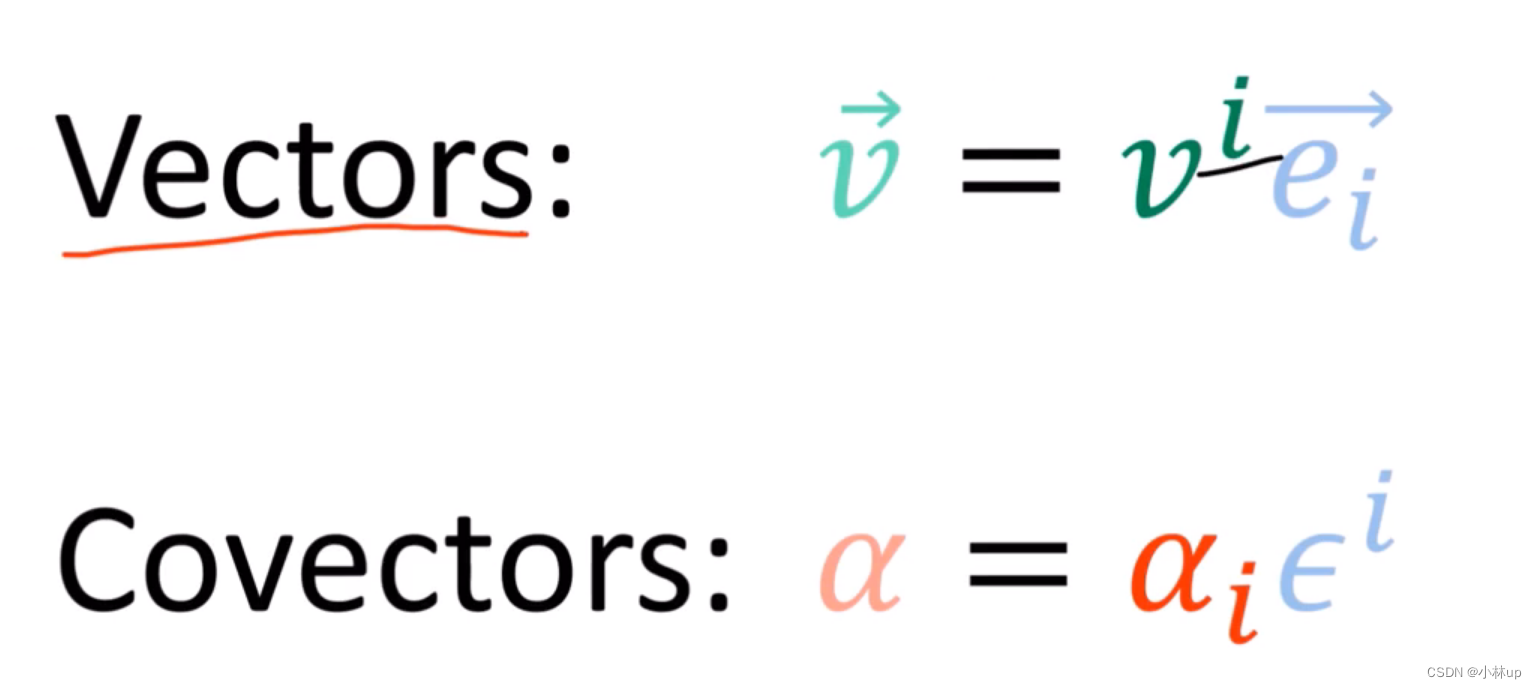
我们要记得向量分量用的是上标,而余向量分量使用的是下标。

将线性映射进行不同的作用我们可以映射到不同的空间。
另一个例子是二次型。


将二次型进行不同的作用我们可以映射到不同的空间。

使用不同的张量空间进行张量积我们得到不同的张量积空间。

在张量的计算中我们可以使用数乘和加法来进行计算:
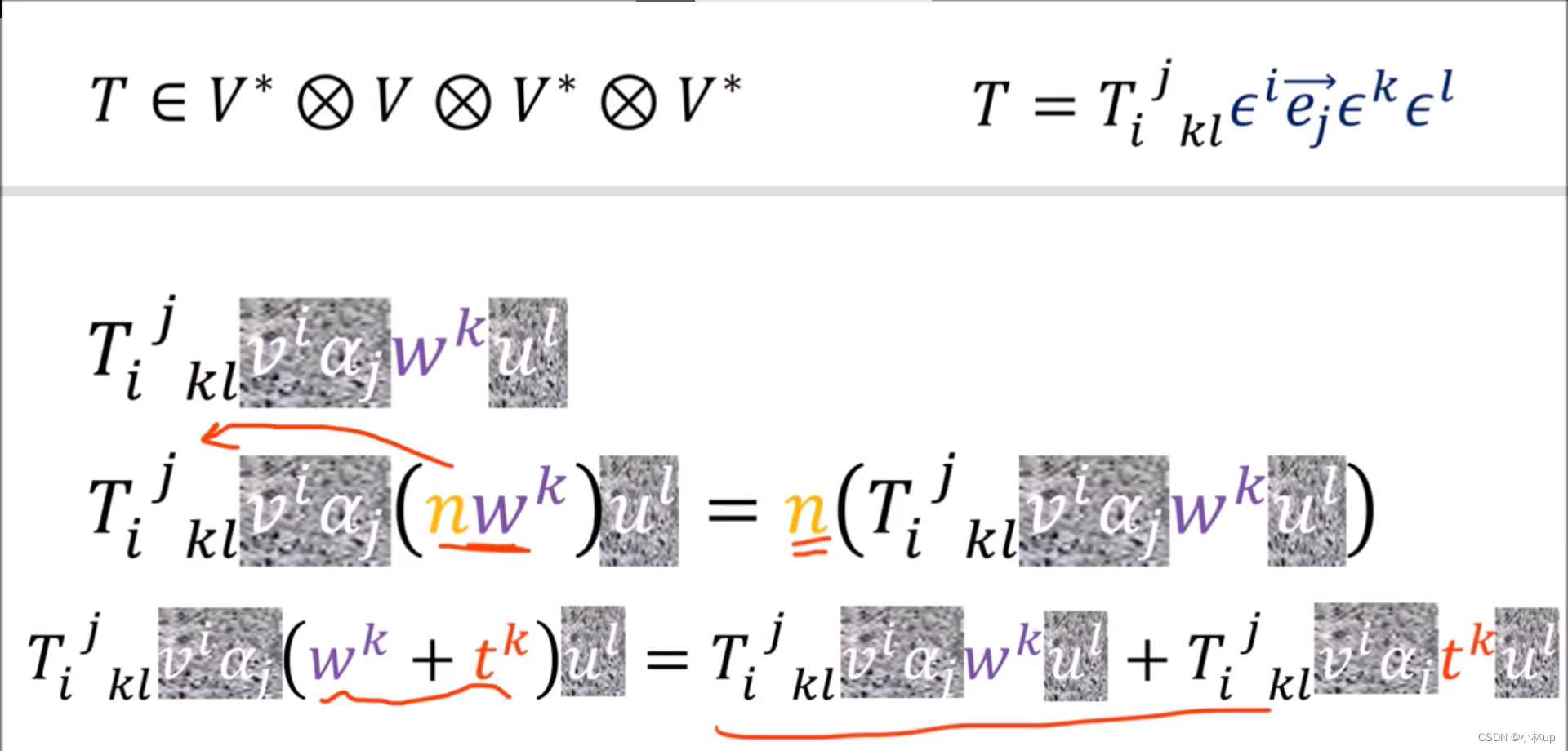
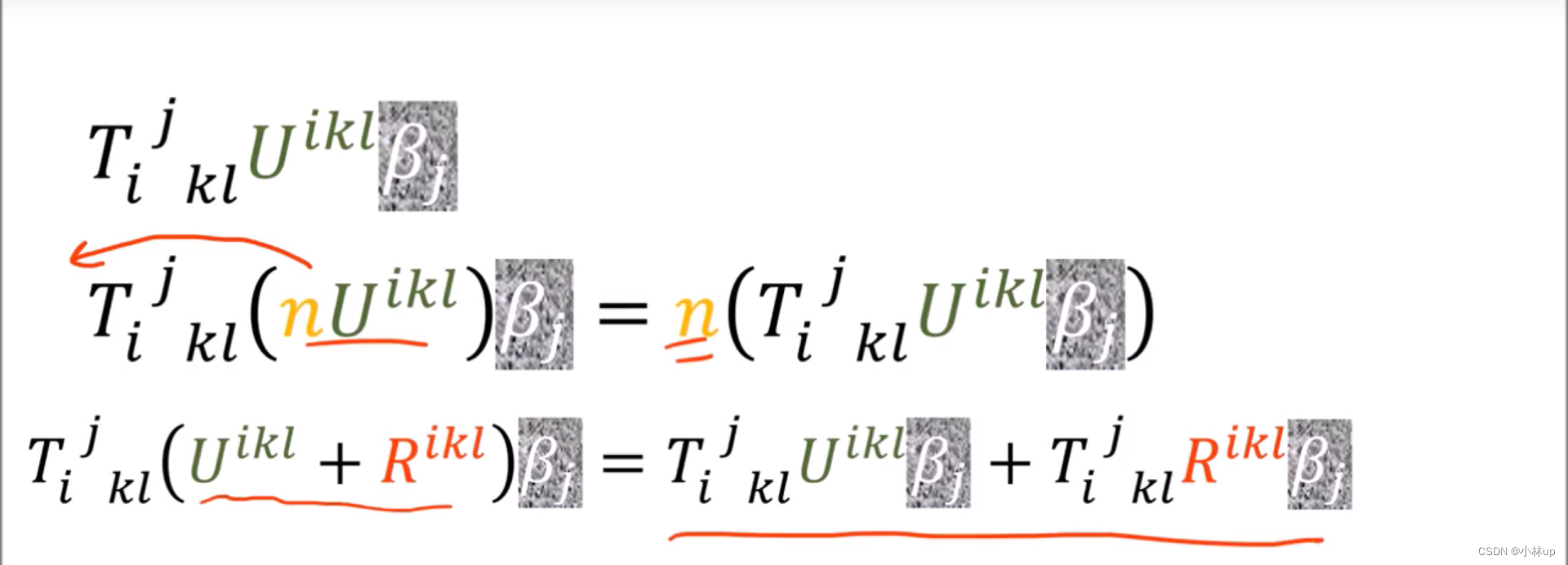
这就引出了高维张量的多线性映射(一个量发生改变,但是其他的量不变,仍然保持线性性):

总结:
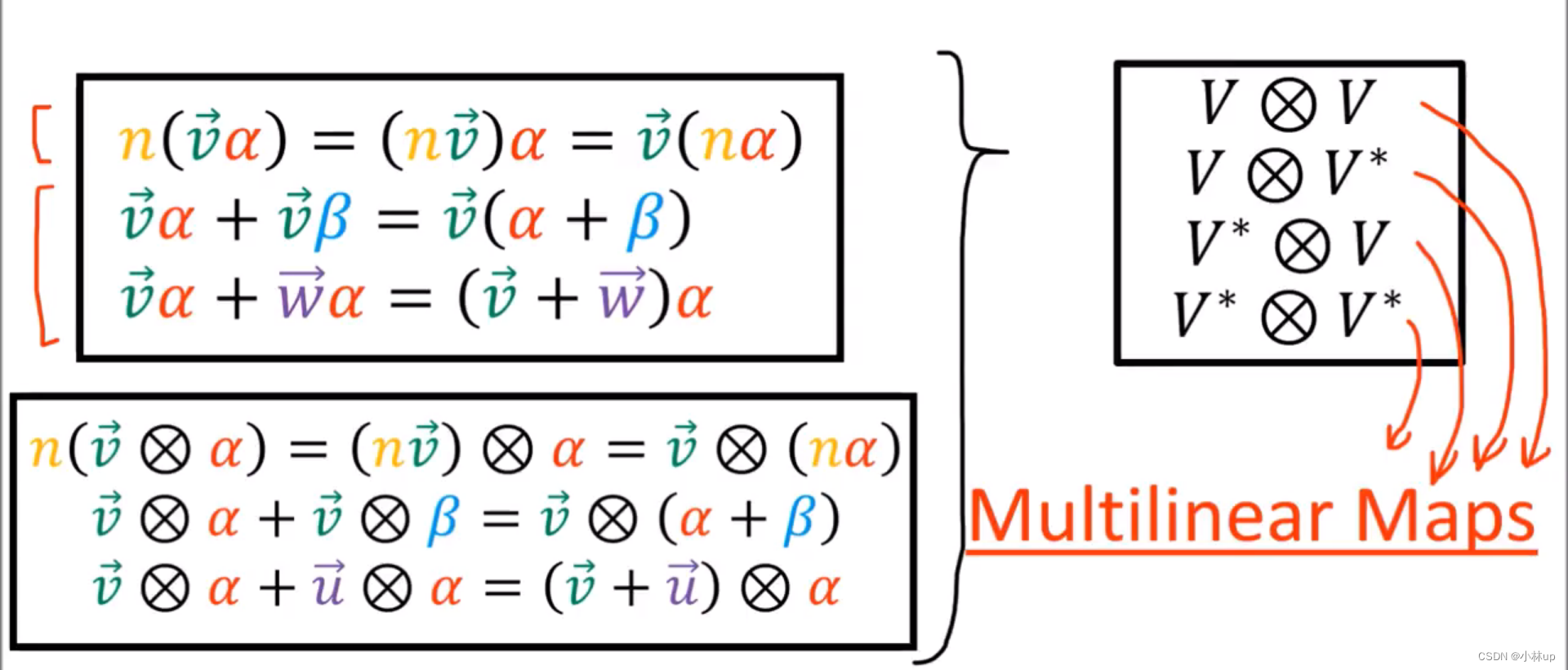
9. 张量指标的上升和下降 Raising or Lowing Indexes
现在我们有两个空间,我们怎么建立两个空间的关系呢?
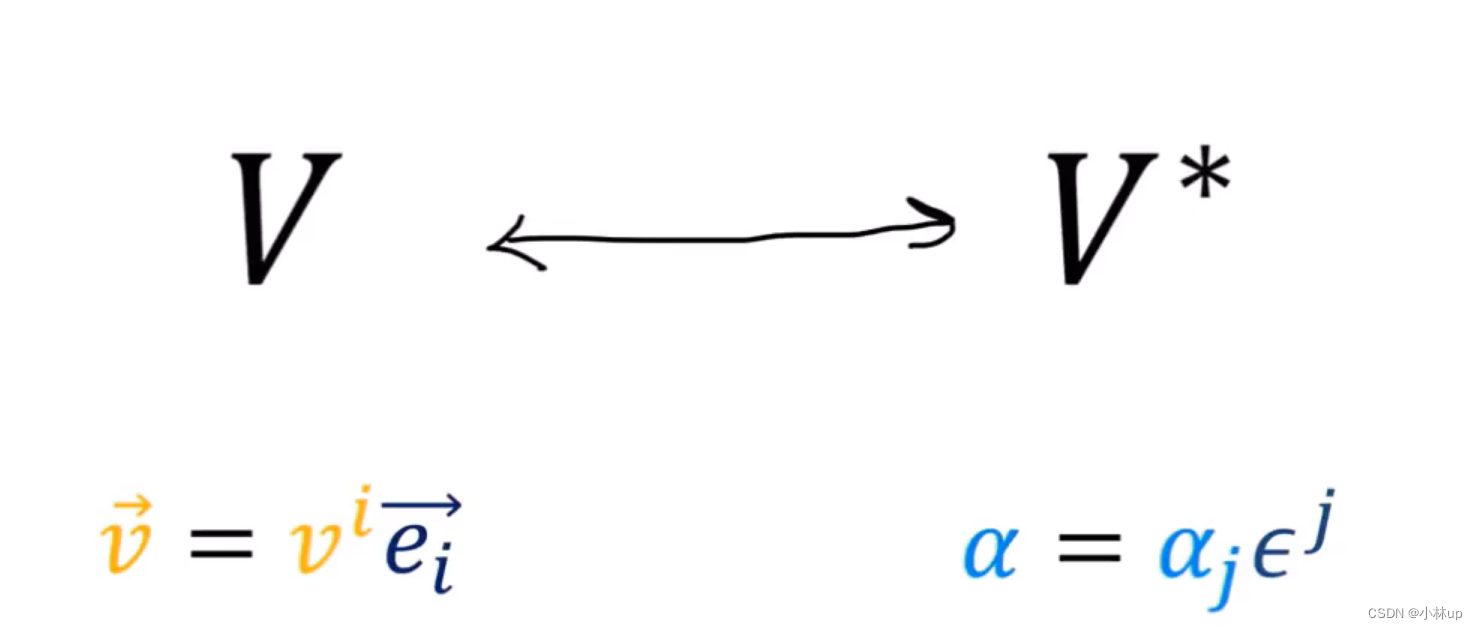
很自然地我们可以想到将它们对应的基进行匹配:


但是这种方法并不好。因为两个坐标转换的规则不一样一个是乘以矩阵
F
F
F,一个是乘以矩阵
B
B
B。
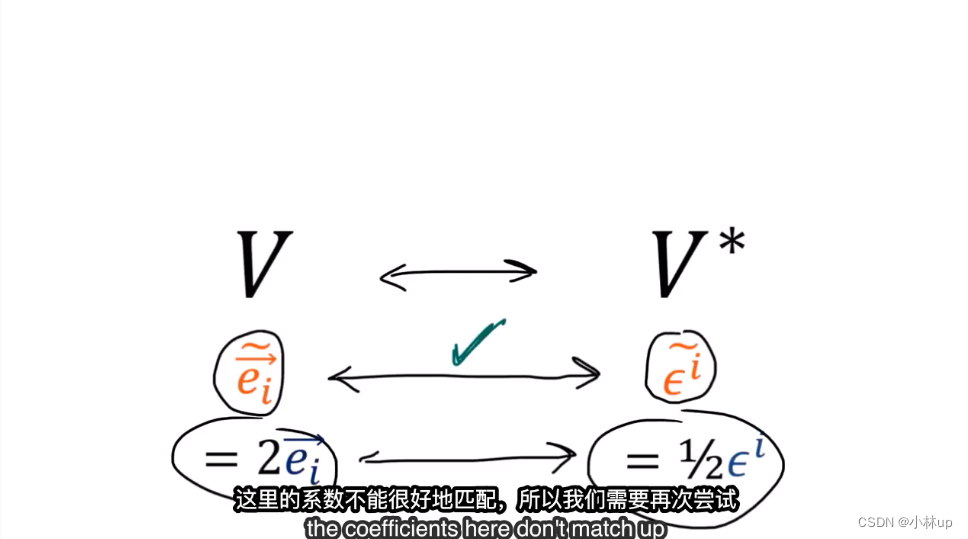
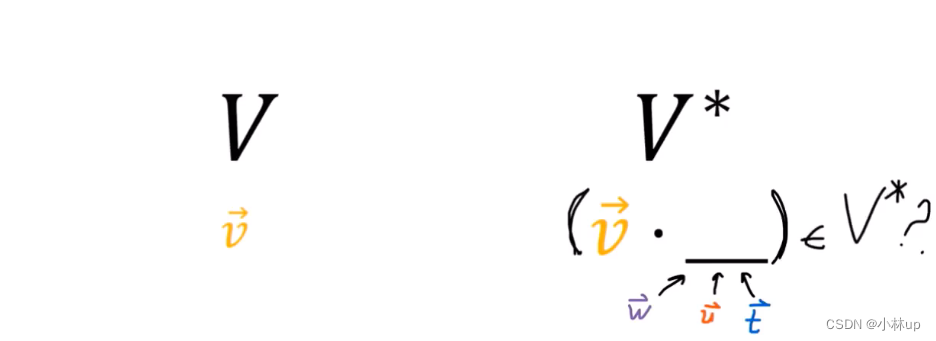
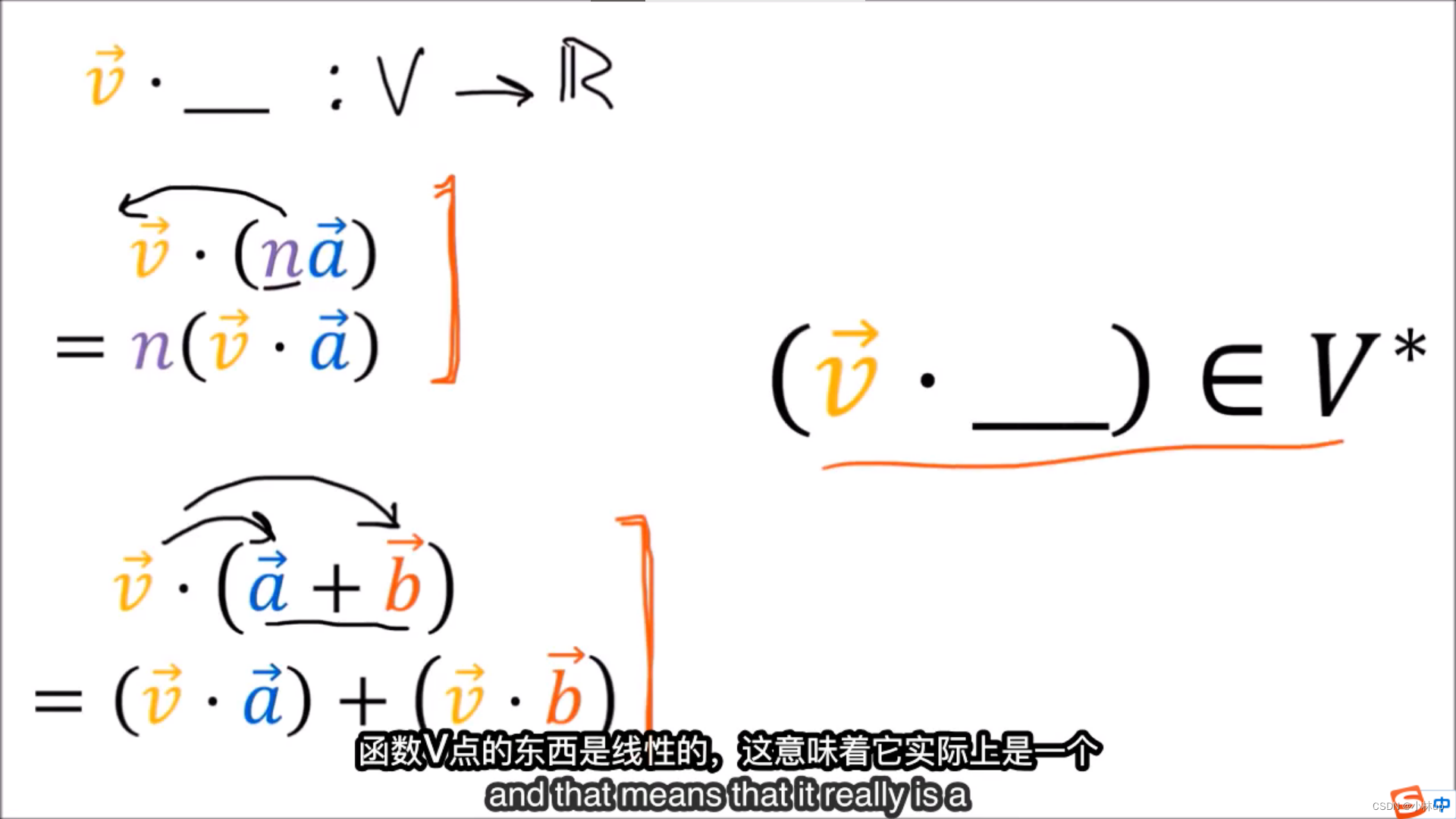
上面的图片表明(
v
⃗
⋅
\vec{v}\cdot
v⋅_)确实属于
V
∗
V^*
V∗。


不依赖于基我们就找到了两者很好的匹配关系。


类比度规张量我们可以得到(
v
⃗
⋅
\vec{v}\cdot
v⋅_)的表达式。

总结:

注意这两个不一样除非
g
i
j
=
δ
i
j
g_{ij}=\delta_{ij}
gij=δij:

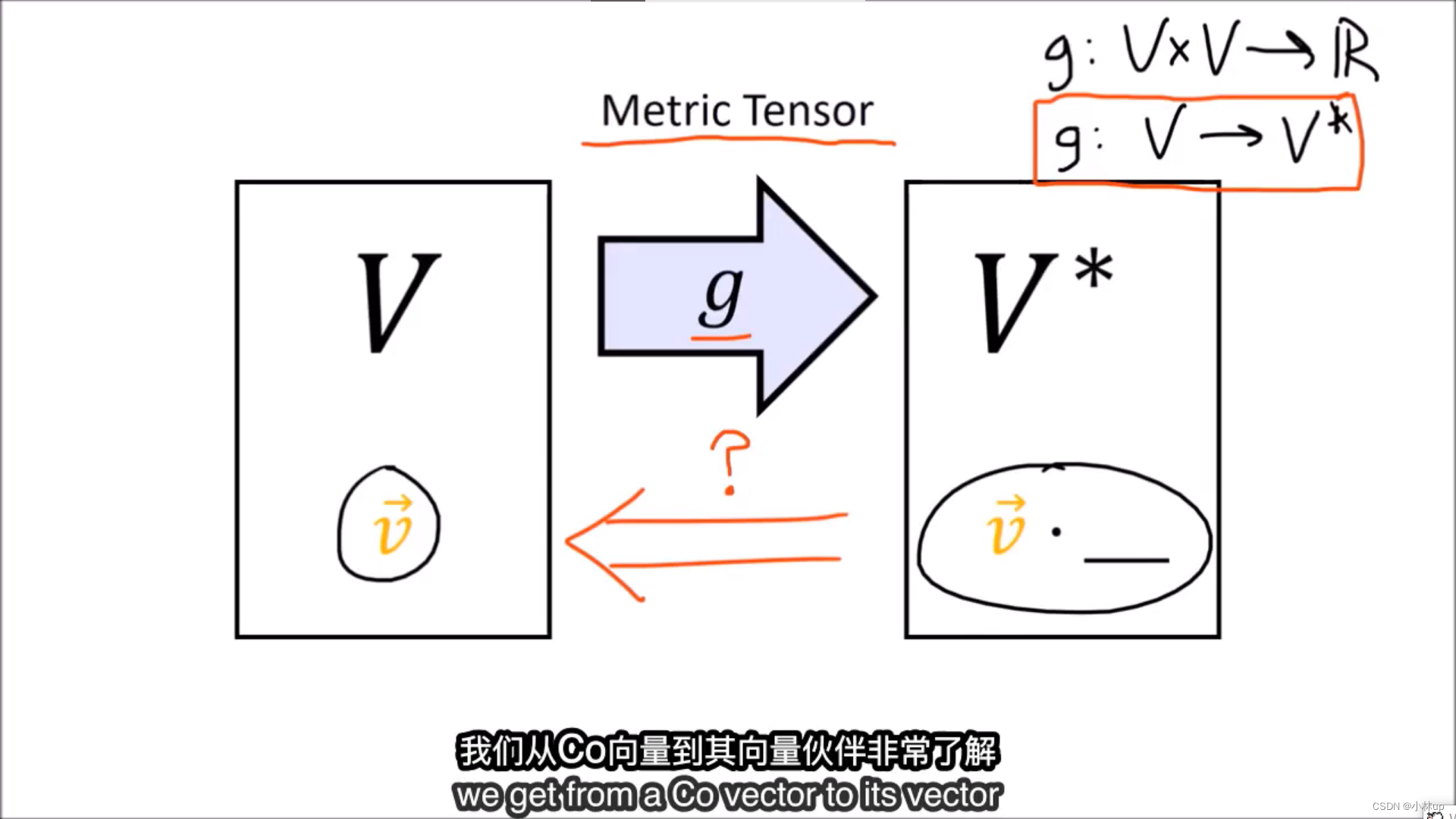
利用
g
g
g可以定义空间
V
V
V到空间
V
∗
V^*
V∗的映射,反过来怎么办呢?

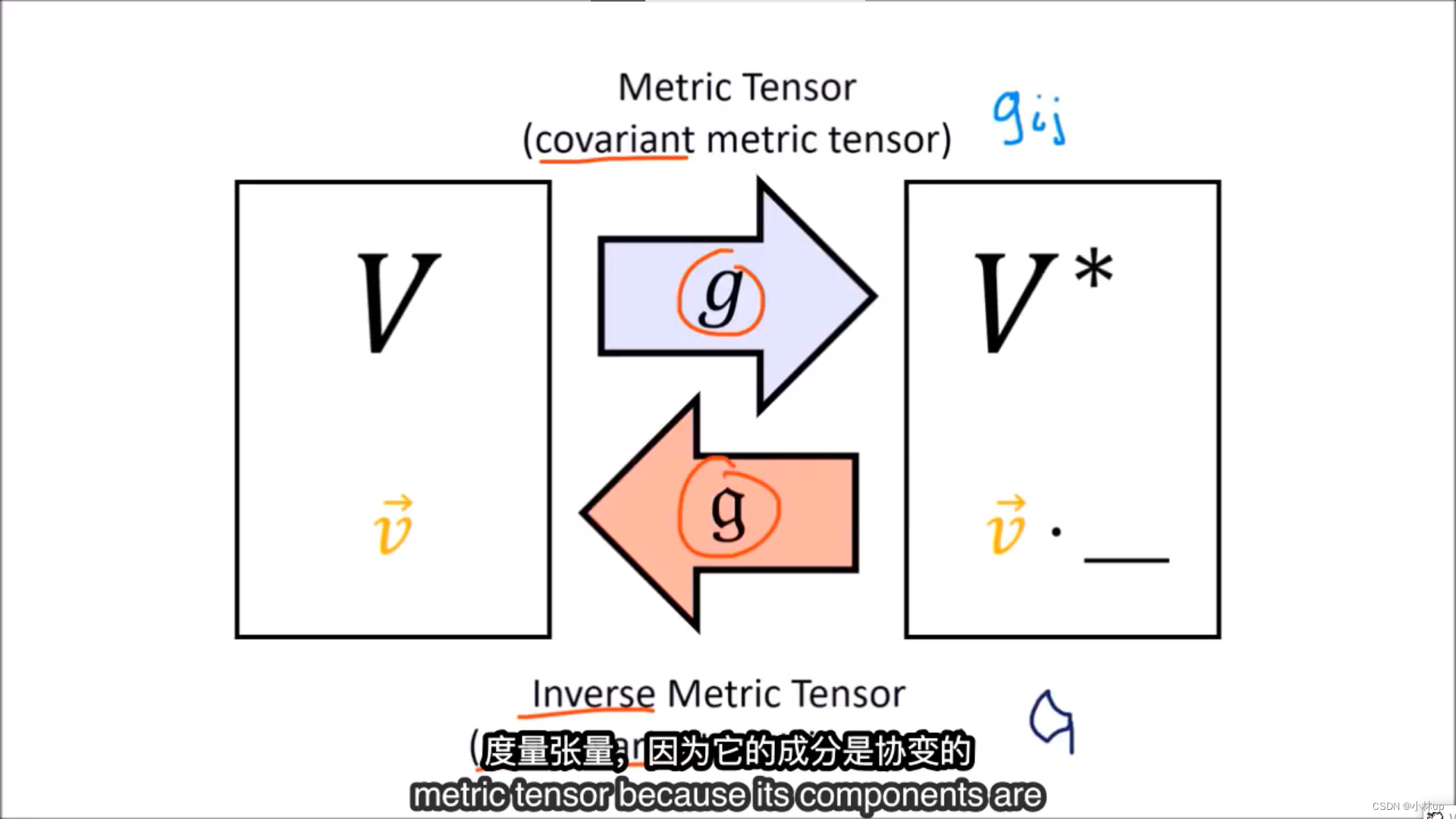
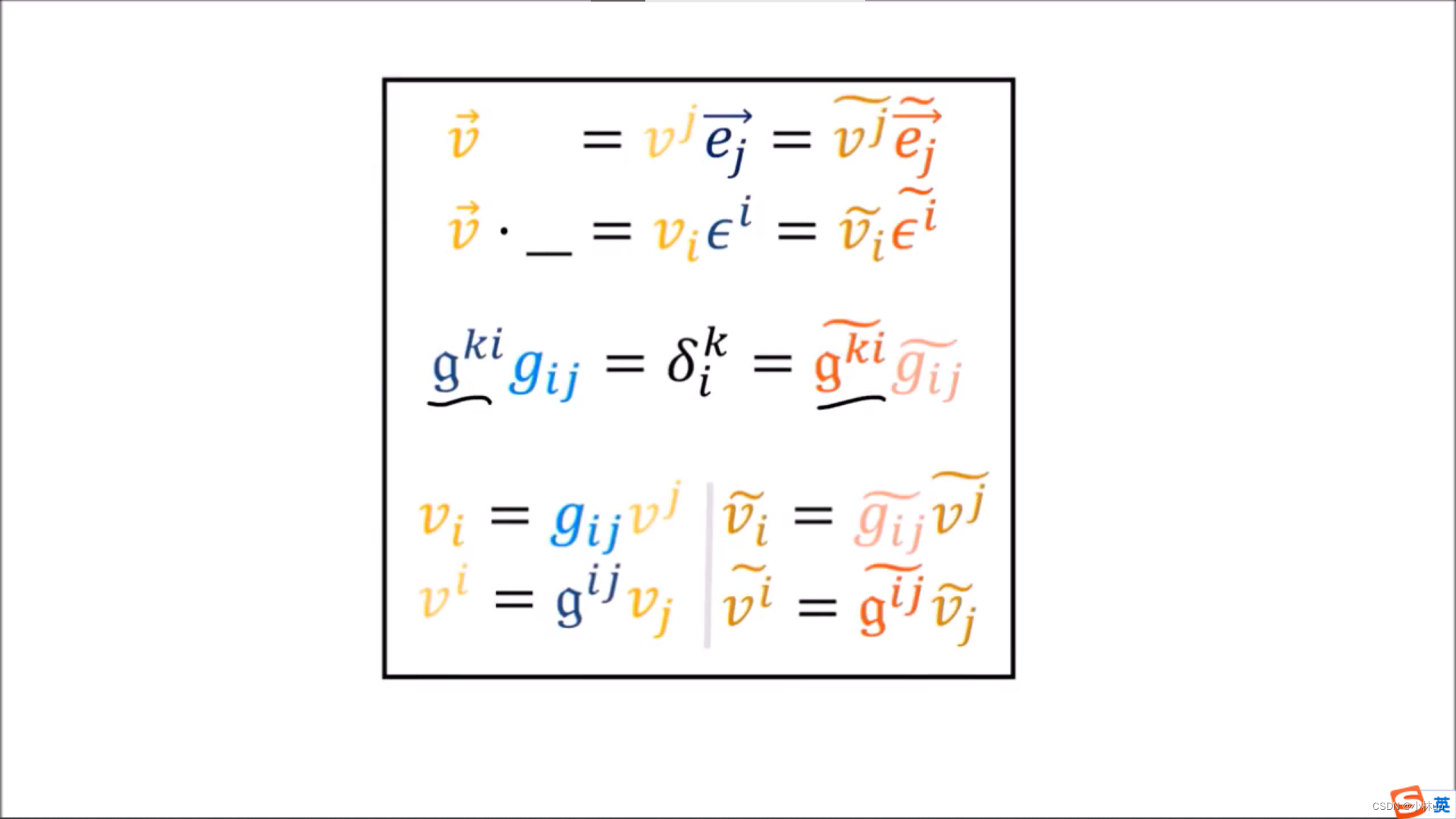
g
g
g把上标变成下标。
g
\mathfrak{g}
g把下标变成上标。

这样我们可以把张量空间进行各种不同的映射。

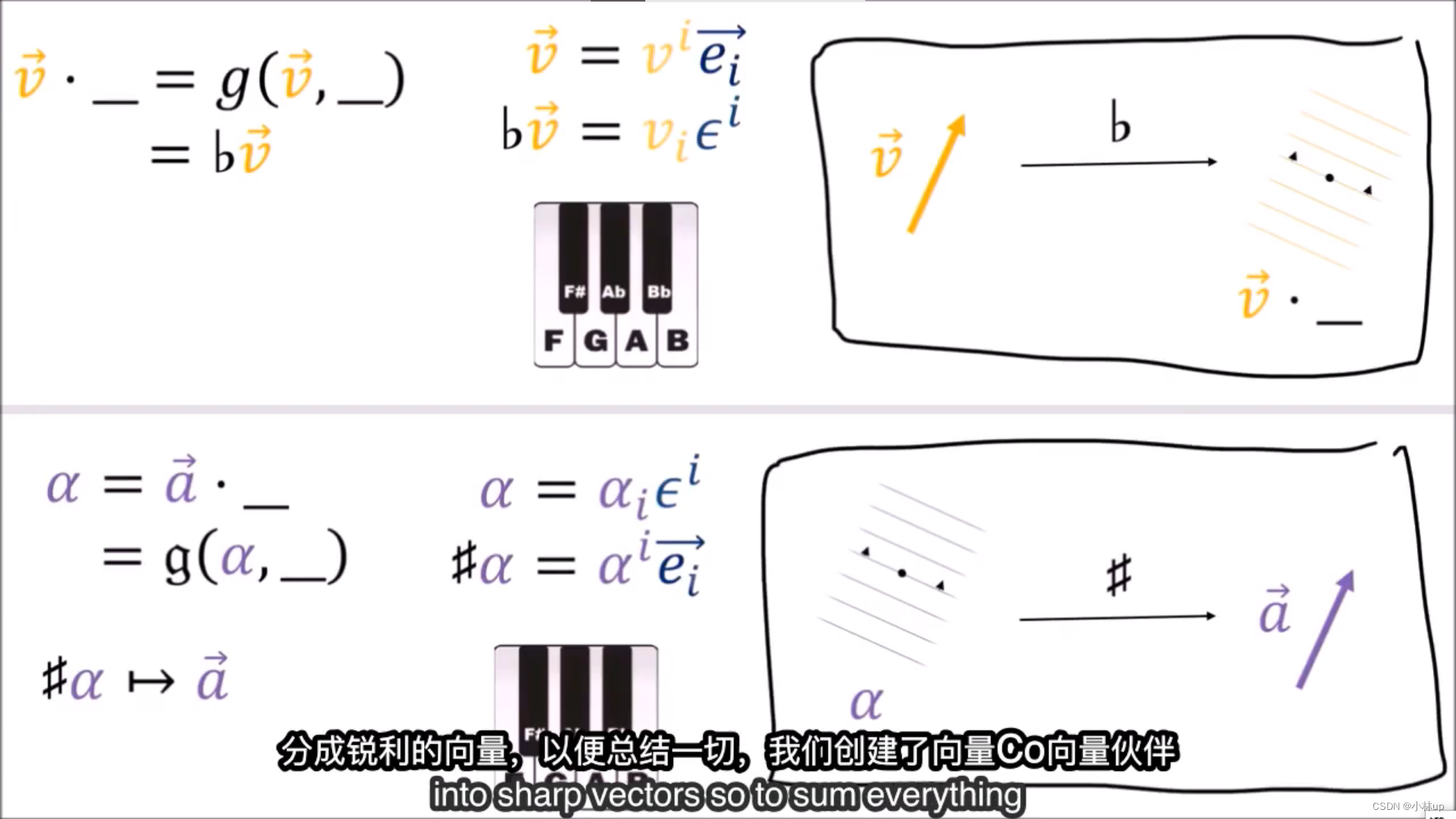
指标从上标变成下标也可以使用符号
b
b
b,从下标变成上标也可以使用符号
#
\#
#,类似于钢琴里的升调和降调。
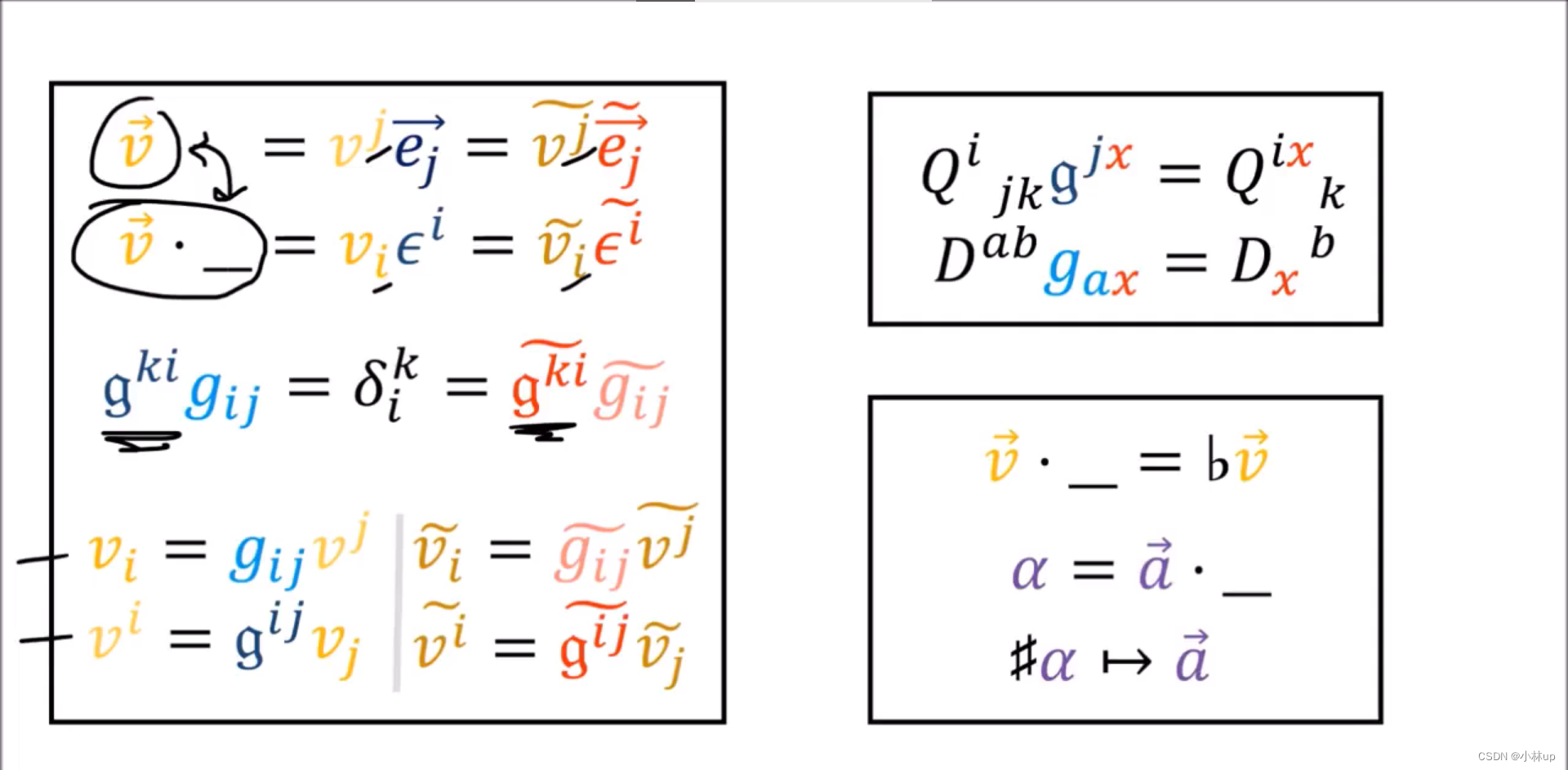
参考:
【机翻】张量分析入门 (Tensor For Beginner)