BM1 反转链表

  给定一个单链表的头结点pHead(该头节点是有值的，，$ 长度为n，反转该链表后，返回新链表的表头。
  数据范围: $0\le n\le 1000$
  要求: 空间复杂度 $O(1)$ ，时间复杂度 $O(n)$ 。
  如当输入链表 { 1 , 2 , 3 } \{1,2,3\} {1,2,3} 时，经反转后，原链表变为 { 3 , 2 , 1 } \{3,2,1\} {3,2,1} ，所以对应的输出为 { 3 , 2 , 1 } \{3,2,1\} {3,2,1} 。

/*
struct ListNode {
	int val;
	struct ListNode *next;
	ListNode(int x) :
			val(x), next(NULL) {
	}
};*/
class Solution {
public:
    ListNode* ReverseList(ListNode* pHead) {
		//考虑空链表
		if (pHead==NULL){return NULL;};
		//反转就是从头开始，依次将*next指向改变
		ListNode *pre = NULL;  // cur的前一个结点，Node中没有，需要额外记录
		ListNode *cur = pHead;
		while(!cur==NULL){  // 对cur指针进行换向
			ListNode *temp = cur->next;
			cur->next = pre;
			// 更新cur和pre
			pre = cur;
			cur = temp;
		}
		return pre;
    }
};

BM2 链表内指定区间反转

  将一个节点数为 size 链表 $m$ 位置到 $\mathrm{n}$ 位置之间的区间反转，要求时间宴杂度 $O(n)$ ，空间复杂度 $O(1)$ 。
例如:
给出的链表为 $1\to 2\to 3\to 4\to 5\to NULL,m=2,n=4$,
返回 $1\to 4\to 3\to 2\to 5\to NULL$.
数据范围: 链表长度 $0<size\le 1000，0<m\le n\le size$ ， 链 表 中 每 个 节 点 的 值 满 足 $|val|\le 1000$
  要求: 时间是杂度 $O(n)$ ，空间宴杂度 $O(n)$
  进阶：时间复杂度 $O(n)$ ，空间复杂度 $O(1)$

答案：

/**
 * struct ListNode {
 *	int val;
 *	struct ListNode *next;
 * };
 */

class Solution {
public:
    /**
     * 
     * @param head ListNode类 
     * @param m int整型 
     * @param n int整型 
     * @return ListNode类
     */
    ListNode* reverseBetween(ListNode* head, int m, int n) {
        // 如果i=0，相当于head被修改，所以不能直接返回head
        ListNode* vHead = new ListNode(-1);
        vHead->next = head;
        // 找到对应的局部完成反转链表
        ListNode* lHead = head;
        ListNode* pre = vHead;
        for(int i =0;i<m-1;i++){ // 注意寻找第m个结点只需要m-1次next
            pre = lHead;
            lHead = lHead->next;
        }
        // 反转链表，注意不能仅仅只进行cur的变向，得用结点交换的思路
        ListNode* cur = lHead;
        for(int i =m;i<n;i++){
            ListNode* temp = cur->next; //暂存cur下一结点位置
            cur->next = temp->next; //保证尾部和原链表剩余部分链接
            temp->next = pre->next; //对下一结点变向
            pre->next = temp; //保证头和
        }

        return vHead->next;
    }
};

注意和BM1 的区别在于，局部反转时，如果还是采用仅cur指针变向，就会造成局部成环，并且局部反转的尾部结点，没有把next和原有链表相连。
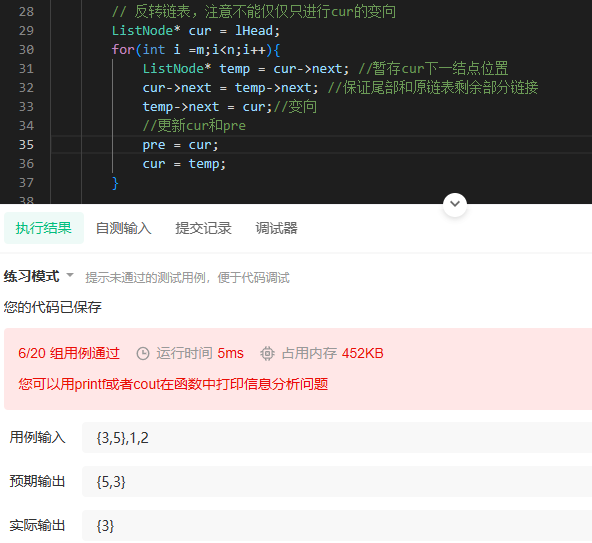
错误示范：

`/**
	 * struct ListNode {
	 *	int val;
	 *	struct ListNode *next;
	 * };
	 */
	class Solution {
	public:
	    /**
	     * 
	     * @param head ListNode类 
	     * @param m int整型 
	     * @param n int整型 
	     * @return ListNode类
	     */
	    ListNode* reverseBetween(ListNode* head, int m, int n) {
	        // 如果i=0，相当于head被修改，所以不能直接返回head
	        ListNode* vHead = new ListNode(-1);
	        vHead->next = head;
	        // 找到对应的局部完成反转链表
	        ListNode* lHead = head;
	        ListNode* pre = vHead;
	        for(int i =0;i<m-1;i++){ // 注意寻找第m个结点只需要m-1次next
	            pre = lHead;
	            lHead = lHead->next;
	        }
	        // 反转链表
	        ListNode* cur = lHead;
	        for(int i =m;i<n;i++){
	            // 将cur的指针变向
	            ListNode* temp = cur->next;
	            cur ->next=pre;
	            // 更新pre和cur
	            pre = cur;
	            cur = temp;
	        }
	
	        return vHead->next;
	    }
	};`

导致结果：

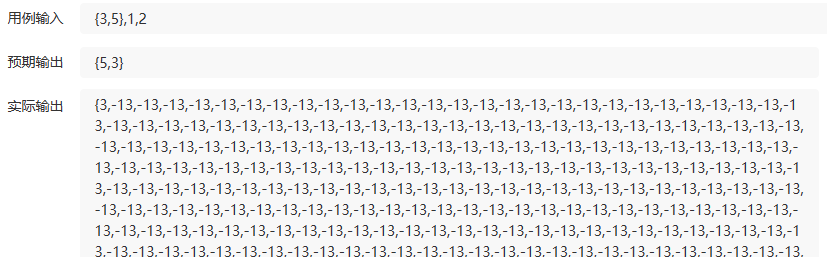
注意就算考虑了尾部相连，但如果还是按照BM1的思路更新pre和cur，然后将局部依次变向，会导致顾尾不顾头