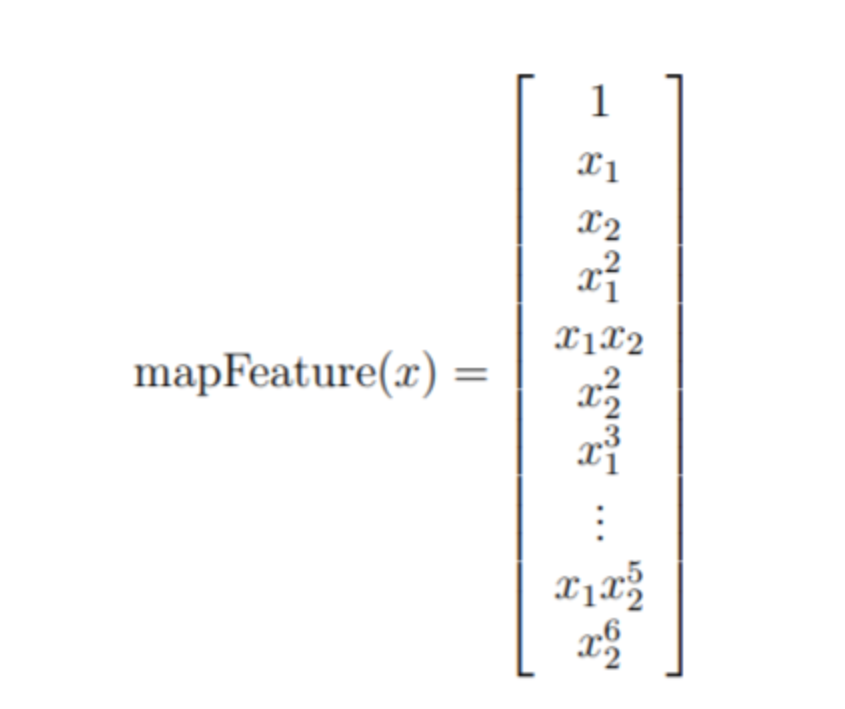
引言

本文简单地介绍一些凸优化(Convex Optimization)的基础知识，可能不会有很多证明推导，目的是能快速应用到机器学习问题上。

凸集

直线与线段

设$x_1\ne x_2$为${\mathbb{R}}^n$空间中的两个点，那么具有下列形式的点
$$y=\theta x_1+(1-\theta )x_2,\theta \in \mathbb{R}$$
组成一条穿越$x_1$和$x_2$的直线。

如果参数$\theta$的值在$0$到$1$之间变动，就构成了$x_1$和$x_2$之间的线段。

仿射集合

如果通过集合$C\subseteq {\mathbb{R}}^n$中任意两个不同点的直线仍然在集合$C$中，那么称集合$C$是仿射的。

可以扩展到多个点的情况，如果${\theta }_1+\cdots +{\theta }_k=1$，我们称具有${\theta }_1{x}_1+\cdots +{\theta }_k{x}_k$形式的点为$x_1,\cdots ,x_k$的仿射组合。

凸集

首先来了解下什么是凸集(Convex Set)。

集合$C$被称为凸集，如果$C$中任意两点间的线段仍然在$C$中，即对于任意$x_1,x_2\in C$和满足$0\le \theta \le 1$的$\theta$都有
$$\theta x_1+(1-\theta )x_2\in C\text{\hspace{1em}(1)}$$

图1. 凸集和非凸集 来自维基百科

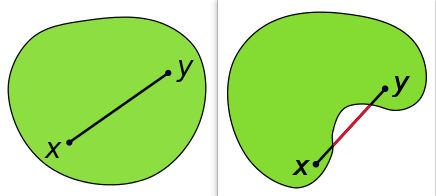
直观上来看，凸集的形状是饱满的，即没有凹进去的地方。

我们称
$$\theta x_1+(1-\theta )x_2\text{\hspace{1em}(2)}$$
为点$x_1,x_2$的凸组合，类似地，可以推广到多个点：
$${\theta }_1{x}_1+\cdots +{\theta }_k{x}_k\text{\hspace{1em}(3)}$$
为点$x_1,\cdots ,x_k$的一个凸组合，其中${\theta }_1+\cdots +{\theta }_k=1$且${\theta }_i\ge 0,i=1,\cdots ,k$。

一个集合是凸集也可以说集合包含其中所有点的凸组合。

我们称集合$C$中所有点的凸组合的集合为其凸包，记作$\text{conv}C$。

多个凸集的交集也是凸集，这意味着如果每个不等式或等式约束条件定义的集合都是凸集，那么这些条件联合起来定义的集合仍然是凸集。

基于凸集的概念可以定义凸函数。

凸函数

函数$f:{\mathbb{R}}^n\to \mathbb{R}$是凸的，如果函数的定义域($\text{dom}f$)是凸集，且对于任意$x_1,x_2\in \text{dom}f$和任意的$0\le \theta \le 1$，有
$$f(\theta x_1+(1-\theta )x_2)\le \theta f(x_1)+(1-\theta )f(x_2)\text{\hspace{1em}(4)}$$

图2. 凸函数示意图 来自维基百科

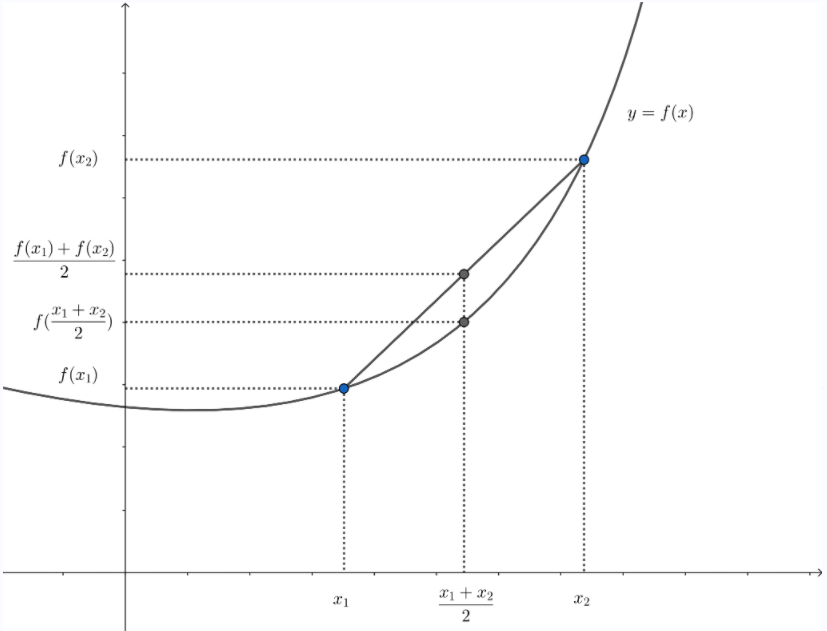
如图2(取$\theta =\frac{1}{2}$)，从几何意义上看，式$(4)$的不等式成立意味着点$(x_1,f(x_1))$和$(x_2,f(x_2))$之间的线段，即从$x_1$到$x_2$的弦，在函数$f$的图像上方。

反之，如果式$(4)$中的函数为$\ge$，则称为凹函数。如果$f$是凸函数，那么$-f$就是凹函数。注意，还有很多函数是非凸也非凹的。

凸函数的一个很好的性质是，它只有一个局部极小值点，同时也是全局最小值点。

凸优化问题

优化问题

我们用
$$\begin{array}{rlrl}& \text{minimize}& & f_0(x)\\ & \text{s.t.}& & f_i(x)\le 0,i=1,\dots ,m\\ & & & h_i(x)=0,i=1,\dots ,p\end{array}\text{\hspace{1em}(5)}$$
描述在所有满足$f_i(x)\le 0,i=1,\cdots ,m$及$h_i(x)=0,i=1,\cdots ,p$的$x$中寻找极小化$f_0(x)$的$x$的问题，即优化问题。

• $x\in {\mathbb{R}}^n$为优化变量；

• 函数$f_0:{\mathbb{R}}^n\to \mathbb{R}$为目标函数；

• 不等式$f_i(x)\le 0$称为不等式约束，相应的函数$f_i:{\mathbb{R}}^n\to \mathbb{R}$称为不等式约束函数；

• 方程组$h_i(x)=0$称为等式约束，相应的函数$h_i:{\mathbb{R}}^n\to \mathbb{R}$称为等式约束函数。

如果没有约束，即$m=p=0$，我们称问题$(5)$为无约束问题。

对目标和所有约束函数有定义的点的集合
$$\mathcal{D}=\bigcap _{i=0}^m\text{dom}{f}_i\cap \bigcap _{i=1}^p\text{dom}{h}_i$$
称为优化问题$(5)$的定义域。当点$x\in \mathcal{D}$满足约束$f_i(x)\le 0,i=1,\cdots ,m$和$h_i(x)=0,i=1,\cdots ,p$时，$x$是可行的。当问题$(5)$至少有一个可行点时，我们称为可行的，否则称为不可行。所有可行点的集合称为可行集或约束集。

如果$x^{\ast }$是可行的并且$f_0(x^{\ast })=p^{\ast }$最优值，我们称$x^{\ast }$为最优点。如果问题存在最优解，我们称最优质是课的或可达的，称问题可解。

如果$x$可行且$f_i(x)=0$，我们称约束$f_i(x)\le 0$的第$i$个不等式在$x$处起作用。如果$f_i(x)<0$，则约束$f_i(x)\le 0$不起作用。我们称约束是冗余的，如果去掉它不改变可行集。

凸优化

凸优化问题是形如
$$\begin{array}{rlrl}& \text{minimize}& & f_0(x)\\ & \text{s.t.}& & f_i(x)\le 0,i=1,\dots ,m\\ & & & a_i^{T}x=b_i,i=1,\cdots ,p\end{array}\text{\hspace{1em}(6)}$$
的问题，其中$f_0,\cdots ,f_m$为凸函数，对比优化问题$(5)$，凸优化问题有三个附加的要求：

1. 目标函数必须是凸的；
2. 不等式约束函数必须是凸的；
3. 等式约束函数$h_i(x)=a_i^T-b_i$必须是仿射的；

立即可以看到一个重要的性质：凸优化问题的可行集是凸的。

带约束的优化问题

拉格朗日乘子法

拉格朗日乘子法(Lagrange Multiplier Method)用于求解带等式约束条件的函数极值(优化问题)。假设有如下极值问题
$$\begin{array}{rlrl}& \text{minimize}& & f(x)\\ & \text{s.t.}& & h_i(x)=0,i=1,\dots ,p\end{array}\text{\hspace{1em}(7)}$$
拉格朗日乘子法构造如下拉格朗日乘子函数
$$L(x,\lambda )=f(x)+\sum _{i=1}^p{\lambda }_i{h}_i(x)\text{\hspace{1em}(8)}$$
其中$\lambda$为新引入的自变量，称为拉格朗日乘子((Lagrange Multiplier)。构造了该函数之后，去掉了对优化变量的等式约束。对拉格朗日乘子函数的所有自变量求偏导，并令其为$0$。包括对$x$求导、对$\lambda$求导。得到下面的方程组：
$$\begin{array}{rl}{\nabla }_{x}f(x)+\sum _{i=1}^p{\lambda }_i{\nabla }_x{h}_i(x)& =0\\ h_i(x)& =0\end{array}\text{\hspace{1em}(9)}$$
求解该方程组即可得到函数的候选极值点。

拉格朗日对偶

对偶是求解最优化问题的一种手段，它将一个最优化问题转换为另一个更容易求解的问题，这两个问题是等价的。

对于如下带等式约束和不等式约束的优化问题：
$$\begin{array}{rlrl}& \text{minimize}& & f(x)\\ & \text{s.t.}& & g_i(x)\le 0,i=1,\dots ,m\\ & & & h_i(x)=0,i=1,\dots ,p\end{array}\text{\hspace{1em}(10)}$$
仿照拉格朗日乘子法构造广义拉格朗日乘子函数
$$L(x,\lambda ,\mu )=f(x)+\sum _{i=1}^m{\lambda }_i{g}_i(x)+\sum _{i=1}^p{\mu }_i{h}_i(x)\text{\hspace{1em}(11)}$$
称$\lambda$和$\mu$为拉格朗日乘子，特别要求${\lambda }_i\ge 0$。接下来将上面的问题转化为所谓的原问题，其最优化解为$p^{\ast }$。
$$p^{\ast }=\underset{x}{\min }\underset{\lambda ,\mu ,{\lambda }_i\ge 0}{\max }L(x,\lambda ,\mu )=\underset{x}{\min }{\theta }_P(x)\text{\hspace{1em}(12)}$$
上式第一个等号右边的含义是先固定变量$x$，将其看成常数，让拉格朗日函数对乘子变量$\lambda$和$\mu$求极大值；消掉(确定了)变量$\lambda$和$\mu$之后，再对变量$x$求极小值。

为了简化表述，定义如下极大值问题
$${\theta }_P(x)=\underset{\lambda ,\mu ,{\lambda }_i\ge 0}{\max }L(x,\lambda ,\mu )\text{\hspace{1em}(13)}$$
这是一个对变量$\lambda$和$\mu$求函数$L$的极大值的问题，将$x$看成常数。这样，原始问题被转化为先对变量$\lambda$和$\mu$求极大值，再对$x$求极小值。

这个原问题和我们要求解的原始问题有同样的解，下面给出证明。对于任意的$x$，分两种情况讨论。

(1)如果$x$是不可行解，对于某些$i$有$g_i(x)>0$，即$x$违反了不等式约束条件，我们让拉格朗日乘子${\lambda }_i=+\infty$，最终使得目标函数${\theta }_P(x)=+\infty$。如果对于某些$i$有$h_i(x)\ne 0$，即违反了等式约束，我们可以让${\mu }_i=+\infty \cdot \text{sgn}(h_i(x))$，从而使得${\theta }_P(x)=+\infty$。

即对于任意不满足等式或不等式约束条件的$x$，${\theta }_P(x)$的值是$+\infty$。

(2)如果$x$是可行解，这时${\theta }_P(x)=f(x)$。因为有$h_i(x)=0$且$g_i(x)\le 0$，而我们要求${\lambda }_i\ge 0$，因为${\theta }_P(x)$的极大值就是$f(x)$。为了达到这个极大值，我们让${\lambda }_i$和${\mu }_i$为$0$，函数$f(x)+{\sum }_{i=1}^p{\mu }_i{h}_i(x)$的极大值就是$f(x)$。

综上两种情况，问题${\theta }_P(x)$和我们要优化的原始问题的关系可以表述为
$${\theta }_P(x)=\{\begin{array}{ll}f(x)& g_i(x)\le 0,h_i(x)=0\\ +\infty & \text{else}\end{array}$$
即${\theta }_P(x)$是原始优化问题的无约束版本。对于任何不可行的$x$，有${\theta }_P(x)=+\infty$，从而使得原始问题的目标函数趋向于无穷大，排除掉$x$的不可行区域，只剩下可行的$x$组成的区域。

这样我们要求解的带约束优化问题被转化成了对$x$不带约束的优化问题，并且二者等价。

下面定义对偶问题与其最优解$d^{\ast }$。
$$d^{\ast }=\underset{\lambda ,\mu ,{\lambda }_i\ge 0}{\max }\underset{x}{\min }L(x,\lambda ,\mu )=\underset{\lambda ,\mu ,{\lambda }_i\ge 0}{\max }{\theta }_D(\lambda ,\mu )\text{\hspace{1em}(14)}$$
这里先固定拉格朗日乘子$\lambda$和$\mu$，调整$x$让拉格朗日函数对$x$求极小值；然后调整$\lambda$和$\mu$对函数求极大值。

原问题和对偶问题只是改变了求极大值和极小值的顺序，每次操控的变量是一样的。如果原问题和对偶问题都存在最优解，则对偶问题的最优值不大于原问题的最优值，即
$$d^{\ast }=\underset{\lambda ,\mu ,{\lambda }_i\ge 0}{\max }\underset{x}{\min }L(x,\lambda ,\mu )\le \underset{x}{\min }\underset{\lambda ,\mu ,{\lambda }_i\ge 0}{\max }L(x,\lambda ,\mu )=p^{\ast }\text{\hspace{1em}(15)}$$
证明，假设原问题的最优解为$x_1,{\lambda }_1,{\mu }_1$，对偶问题的最优解为$x_2,{\lambda }_2,{\mu }_2$，由于原问题是先对$(\lambda ,\mu )$取极大值，有
$$L(x_1,{\lambda }_1,{\mu }_1)\ge L(x_1,{\lambda }_2,{\mu }_2)$$
这里固定$x_1$。

而对偶问题先对$x$取极小值，有
$$L(x_2,{\lambda }_2,{\mu }_2)\le L(x_1,{\lambda }_2,{\mu }_2)$$
这类变化的只是$x$。上面两个式子中右边都是一样的，从而有
$$L(x_1,{\lambda }_1,{\mu }_1)\ge L(x_2,{\lambda }_2,{\mu }_2)$$
这一结论称为弱对偶定理(Weak Duality)。

原问题最优值和对偶问题最优值的差$p^{\ast }-d^{\ast }$称为对偶间隙。如果原问题和对偶问题有相同的最优解，那么我们就可以把求解原问题转化为求解对偶问题，此时对偶间隙为0，这种情况称为强对偶。

但要满足怎样的条件才能使得$d^{\ast }=p^{\ast }$呢，就是下面阐述的KKT条件。

KKT条件

KKT(Karush-Kuhn-Tucker)条件用于求解带有等式和不等式约束的优化问题，是拉格朗日乘子法的推广。

对于如下带等式约束和不等式约束的优化问题：
$$\begin{array}{rlrl}& \text{minimize}& & f(x)\\ & \text{s.t.}& & g_i(x)\le 0,i=1,\dots ,m\\ & & & h_i(x)=0,i=1,\dots ,n\end{array}\text{\hspace{1em}(16)}$$
与拉格朗日对偶的做法类似，为其构造拉格朗日乘子函数消掉等式和不等式约束：
$$L(x,\lambda ,\mu )=f(x)+\sum _{i=1}^m{\mu }_i{g}_i(x)+\sum _{i=1}^n{\lambda }_i{h}_i(x)\text{\hspace{1em}(17)}$$
$\lambda$和$\mu$称为KKT乘子。

KKT条件包括：

1. ${\nabla }_{x}L(x,\lambda ,\mu )=0$
2. $g_i(x)\le 0$
3. $h_i(x)=0$
4. ${\mu }_i\ge 0$
5. ${\mu }_i{g}_i(x)=0$

其中第三个条件$h_i(x)=0$等式约束和第二个条件$g_i(x)\le 0$不等式约束是本身应该满足的约束；第一个条件${\nabla }_{x}L(x,\lambda ,\mu )=0$和拉格朗日乘子法相同。

第四个条件称为对偶可行性条件；

第五个条件称为互补松弛条件，而且当一个变量取非零值时，另一个变量必须取零。

KKT条件是取得极值的必要条件，但如果一个优化问题是凸优化问题，则KKT条件是取得极小值的充分条件。

Slater条件

Slater条件：一个凸优化问题如果存在一个候选$x$使得所有不等式约束都是严格满足的，即对于所有的$i$都有$g_i(x)<0$，也就是说，在不等式约束区域内部至少有一个可行点，则存在$(x^{\ast },{\lambda }^{\ast },{\mu }^{\ast })$使得它们同时为原问题和对偶问题的最优解，即
$$p^{\ast }=d^{\ast }=L(x^{\ast },{\lambda }^{\ast },{\mu }^{\ast })$$
Slater条件是强对偶成立的充分条件而不是必要条件。

小结

Slater条件和KKT条件都是用来判断最优化问题是否有解的条件。它们之间的关系可以总结如下：

• Slater条件是一种充分条件，当最优化问题满足Slater条件时，会保证强对偶性成立，并且原始问题和对偶问题都存在最优解。具体来说，Slater条件要求不等式约束条件 $g_i(x)\le 0$ 和等式约束条件 $h_i(x)=0$ 满足严格可行性，即存在一个$x$使得所有的不等式约束条件 $g_i(x)<0$ 均严格成立。
• KKT条件是一组必要条件，可以用于判断某个点是否为最优解。对于有约束的最优化问题，其KKT条件包括互补松弛条件、不等式约束条件的拉格朗日乘子大于等于零以及梯度为零。若最优化问题的解满足KKT条件，则该解是最优解的必要条件。

需要注意的是，Slater条件只是强对偶性的一种充分条件，而不是必要条件。也就是说，如果一个问题不满足Slater条件，仍然有可能存在最优解以及强对偶性。而KKT条件则是最优解的必要条件，但不一定是充分条件，也就是说，一个满足KKT条件的点并不一定是最优解。

因此，在实际求解问题时，我们通常需要结合Slater条件和KKT条件来进行判断，以保证得到的解是可行的、正确的，并且满足约束条件。

最优化方法

梯度下降法

梯度下降法(gradient descent)或最速下降法是求解无约束最优化问题的一种最常用的方法，它的优点是实现简单。梯度下降法是一种迭代算法，每一步需要求解目标函数的梯度向量。

假设$f(x)$是${\mathbb{R}}^n$是具有一阶连续偏导数的函数。要求解的无约束最优化问题是
$$\underset{x\in {\mathbb{R}}^n}{\min }f(x)\text{\hspace{1em}(18)}$$
$x^{\ast }$表示目标函数$f(x)$的极小值点。

梯度下降法通过选择适当的初值$x^{(0)}$，不断迭代，更新$x$的值，进行目标函数的极小化，直到收敛。由于负梯度方向是使函数值下降最快的方向，在迭代的每一步，以负梯度方向更新$x$的值，从而达到减少函数值的目的。

由于$f(x)$具有一阶连续偏导数，若第$k$次迭代值为$x^{(k)}$，则可将$f(x)$在$x^{(k)}$附近进行一阶泰勒展开：
$$f(x)=f(x^{(k)})+g_k^T(x-x^{(k)})\text{\hspace{1em}(19)}$$
在人工智能高等数学中我们知道在$x=a$点的泰勒展开式为：
$$g(x)=f(a)+\frac{f^{\prime }(a)}{1!}(x-a)+\frac{f^{\prime \prime }(a)}{2!}(x-a{)}^2+\frac{f^3(a)}{3!}(x-a{)}^3+...+\frac{f^n(a)}{n!}(x-a{)}^n\text{\hspace{1em}(20)}$$
这里去掉了高阶项就得到了公式$(19)$，$g_k=g(x^{(k)})=\nabla f(x^{(k)})$为$f(x)$在$x^{(k)}$的梯度，即一阶偏导。

求出第$k+1$次迭代值$x^{(k+1)}$：
$$x^{(k+1)}\leftarrow x^{(k)}+{\lambda }_k{p}_k\text{\hspace{1em}(21)}$$
其中，$p_k$是搜索方向，取负梯度方向$p_k=-\nabla f(x^{(k)})$，${\lambda }_k$是步长，这里由一维搜索确定，即找到${\lambda }_k$使得
$$f(x^{(k)}+{\lambda }_k{p}_k)=\underset{\lambda \ge 0}{\min }f(x^{(k)}+\lambda p_k)\text{\hspace{1em}(22)}$$

一维搜索是一种优化算法，也被称为线性搜索。在机器学习中，一维搜索通常是用来确定如何更新模型参数的步长或学习率，以最小化训练数据上的损失函数。

一维搜索可以简单理解为在某个方向上寻找一个合适的步长，使得当前位置向这个方向前进这个步长之后，能够使目标函数（或者损失函数）达到最小值。其实现过程通常是沿着负梯度方向进行搜索，并通过逐步缩小搜索范围和增加精度等方法，找到一个近似的最优解。

因为一维搜索只在一个方向上进行搜索，在复杂的高维问题中很少直接使用，通常会作为其他更复杂优化算法的辅助手段。

梯度下降法算法如下：

输入： 目标函数$f(x)$，梯度函数$g(x)=\nabla f(x)$，计算精度$ϵ$；

输出： $f(x)$的极小点$x^{\ast }$。

(1) 取初值$x^{(0)}\in {\mathbb{R}}^n$，令$k=0$。

(2) 计算$f(x^{(k)})$。

(3) 计算梯度$g_k=g(x^{(k)})$，当$||g_k||<ϵ$时，停止迭代，令$x^{\ast }=x^{(k)}$；否则，令$p_k=-g(x^{(k)})$，求${\lambda }_k$使
$$f(x^{(k)}+{\lambda }_k{p}_k)=\underset{\lambda \ge 0}{\min }f(x^{(k)}+\lambda p_k)$$
(4) 置$x^{(k+1)}=x^{(k)}+{\lambda }_k{p}_k$，计算$f(x^{(k+1)})$

当$||f(x^{(k+1)})-f(x^{(k)})||<ϵ$或$||x^{(k+1)}-x^{(k)}||<ϵ$时，停止迭代，令$x^{\ast }=x^{(k+1)}$。

(5) 否则，置$k=k+1$，转(3)。

当目标函数是凸函数时，梯度下降法的解释全局最优解。但一般情况下，其解不保证是全局最优解。且收敛速度也未必是很快的。

如果是无约束优化问题，想要收敛速度快的话，可以考虑牛顿法或拟牛顿法。

牛顿法和拟牛顿法都是求解无约束最优化问题的常用方法，具有收敛速度快的优点。牛顿法是迭代算法，每一步需要求解目标函数的海森矩阵的逆矩阵，计算比较复杂，而且有时候海森矩阵不一定存在逆阵。拟牛顿法通过正定矩阵近似海森矩阵的逆矩阵或海森矩阵，简化了这一计算过程。