1-旋转数组的最小数字(11)
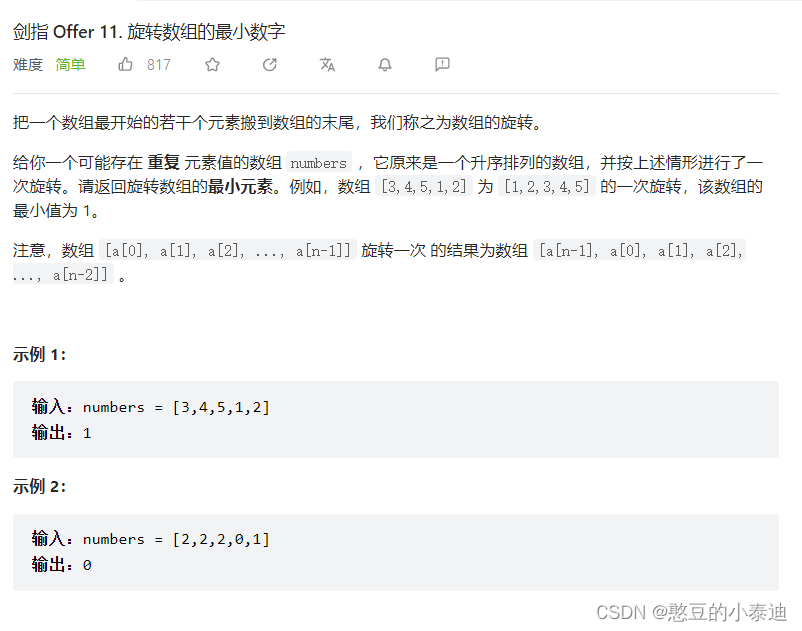
主要思路:
一次旋转将最后一个元素移动最前面,由于数组最开始是升序的,因此数组的大部分元素都应该保持升序的状态(n1<n2<...<n3>n4<n5<...<n6);
最后面开始遍历,只要遇到一个元素小于其前一个元素(numbers[i] < numbers[i - 1]),则numbers[i],就是最小的元素,因为前面的元素都是旋转移动过去的。
// 利用遍历
class Solution {
public:
int minArray(vector<int>& numbers) {
int size = numbers.size();
for(int i = size - 1; i > 0; i--){
if(numbers[i] < numbers[i - 1]){
return numbers[i];
}
}
return numbers[0];
}
};// 利用二分法
class Solution {
public:
int minArray(vector<int>& numbers) {
int low = 0;
int high = numbers.size() - 1;
while (low < high) {
int pivot = low + (high - low) / 2;
if (numbers[pivot] < numbers[high]) {
high = pivot;
}
else if (numbers[pivot] > numbers[high]) {
low = pivot + 1;
}
else {
high -= 1;
}
}
return numbers[low];
}
};2--矩阵中的路径(12)

视频讲解参考:剑指 Offer 12. 矩阵中的路径
主要思路:
遍历 board 中的每一个位置,判断当前位置的元素是否与word[k]相同,并递归判断其上左下右四个元素是否与word[k+1]相同;如果word所有字符都匹配,则返回true,否则返回false并遍历board的下一个元素;
为了防止重复访问元素,在判断一个位置上左下右四个元素时,将当前元素用特殊字符mask掉(当其被重复访问时,一定是返回false),避免其被重复访问;
代码:
#include <vector>
#include <string>
#include <iostream>
class Solution {
public:
bool exist(std::vector<std::vector<char>>& board, std::string word) {
for(int i = 0; i < board.size(); i++){
for(int j = 0; j < board[0].size(); j++){
if(dfs(board, word, i, j, 0)){ // 搜索每一个字符
return true;
}
}
}
return false;
}
bool dfs(std::vector<std::vector<char>>& board, std::string word, int i, int j, int k){
// 判断是否越界、当前board[i][j]是否等于word[k]
if(i >= board.size() || i < 0 || j >= board[0].size() || j < 0 || board[i][j] != word[k]){
return false;
}
if (k == (word.length() - 1)){ // word的所有字符全部匹配成功
return true;
}
// 通过上面的if循环,可知当前board[i][j] == word[k]
// 将当前 board[i][j] mask掉,防止被重复访问
board[i][j] = '#';
// 重复调用dfs,判断board[i][j]上左下右四个字符是否与word[k+1]相同
bool result = dfs(board, word, i-1, j, k+1) || dfs(board, word, i, j-1, k+1)
|| dfs(board, word, i+1, j, k+1) || dfs(board, word, i, j+1, k+1);
// 返回前,恢复mask掉的board[i][j]
board[i][j] = word[k];
return result;
}
};
int main(int argc, char* argv[]){
std::vector<std::vector<char>> board;
std::vector<char> b0 = {'A', 'B', 'C', 'E'};
std::vector<char> b1 = {'S', 'F', 'C', 'S'};
std::vector<char> b2 = {'A', 'D', 'E', 'E'};
board.push_back(b0);
board.push_back(b1);
board.push_back(b2);
std::string word = "ABCCED";
Solution s1;
bool status = s1.exist(board, word);
std::cout << status << std::endl;
return 0;
}
3--机器人的运动范围

主要思路:
与《矩阵中的路径》类似,可利用深度优先递归判断每一个方格是否可跳,可跳条件是数位之和不大于 k;
机器人的运动范围必须从(0, 0)开始,当访问某个可行方格后,可利用一个二维数组记录其已被访问,最后统计二维数组即可确定可访问的方格数;
同时一个方格上、下、左、右移动可优化为只向右和向下移动,因为任何一个可跳方格都可以由上一个可行方格通过向右和向下移动得到,节省了递归四个方向的消耗(具体可看官方解释);
#include <vector>
#include <iostream>
class Solution {
public:
int movingCount(int m, int n, int k) {
for(int j = 0; j < n; j++){
tmp.push_back(0);
}
for(int i = 0; i < m; i++){
v.push_back(tmp);
}
DFS(0, 0, m, n, k);
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(v[i][j] == 1){
num++;
}
}
}
return num;
}
void DFS(int i, int j, int m, int n, int k){
// 越界、已访问
if(i < 0 || i >= m || j < 0 || j >= n || v[i][j] == 1){
return;
}
bool status = Cal_ij(i, j, k);
if (status) v[i][j] = 1;
else return; // 不能进入该点,也就不能从该点移动到其它四个点,直接返回
// DFS(i-1, j, m, n, k);
// DFS(i, j-1, m, n, k);
DFS(i+1, j, m, n, k); // 向右移动
DFS(i, j+1, m, n, k); // 向下移动
}
bool Cal_ij(int i, int j, int k){
int sum = 0;
sum += i % 10;
i = i / 10;
sum += i;
sum += j % 10;
j = j / 10;
sum += j;
if(sum > k) return false;
else return true;
}
private:
std::vector<std::vector<int>> v;
std::vector<int> tmp;
int num = 0;
};
int main(int argc, char *argv[]){
int m = 16;
int n = 8;
int k = 4;
Solution s1;
int num = s1.movingCount(m, n, k);
std::cout << "num is: " << num << std::endl;
}