一、堆
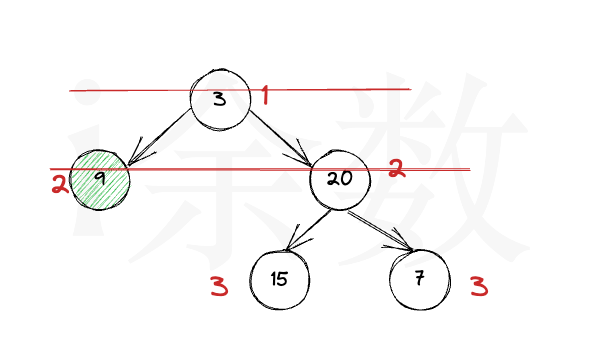
1,堆结构就是用数组实现的完全二叉树结构
根节点的左孩子的下标为:2i+1,右孩子为2i+2。两个孩子的父节点为(i-1)/2向下取整
2,完全二叉树中如果每棵子树的最大值都在顶部就是大根堆
从下往上将孩子与父节点进行比较,如果子叶节点的数值大于根节点,则互换,反之则停止向上比较
3,完全二叉树中如果每棵子树的最小值都在顶部就是小根堆
与大根堆相反
4,堆结构的heapInsert与heapify操作
以上大根堆与小根堆的比较就是heapInsert的过程;
大根堆heapInsert的代码演示:
void heapify(vector<int> &a, int index)
{
while (a[index] > a[(index - 1) / 2])
{
//两个元素互换
swap(a, a[index], a[(index - 1) / 2]);
//向上反馈
index = (index - 1) / 2;
}
}
heapify操作:
这里举一个例子,当用户想要删除大根堆中的最大值,我们首先要将数组中最后一个数覆盖到数组中的0位置,然后根节点开始与两个子叶节点的最小值进行互换,然后被换之后再将换下来的根节点与当前位置的两个子叶节点进行比较互换操作。
void heapify(vector<int> &a, int index, int heapsize)
{
//index表示从何位置开始进行heapify操作操作
//heapsize表示数组的长度
//设置左孩子的下标
int left = index*2+1;
//如果当前根节点还有叶节点,则操作
while(left < heapsize)
{
//两个孩子中,谁的值大,则把下标给largest
int largest = left + 1 < heapsize && a[left+1] > a[left]? left+1 : left;
//父和孩子之间的最大值谁最大,将下标给largest
largest = a[largest] > a[index] ? largest :index;
//如果最大值就是根节点,则退出
if(largest == index)
break;
//否则则交换
swap(a, index, largest);
index = largest;
left = index*2+1;
}
}
二、堆排序
思路:
1、将数组排列成堆结构,并通过heapInsert操作组成一个大根堆
2、将大根堆的0号位置的节点与最后一个节点互换,heapsize减1,并将堆中最后一个元素放到0位置,进行heapify操作
3、重复2步骤直至堆的大小为0,结束操作
动图展示:

代码实现:
void heapify(vector<int>&a, int index1, int heapsize)
{
//进行heapifty
//设置左孩子的节点
int left = 2 * index1 + 1;
//如果有左孩子,则开始进行heapifty
while (left < heapsize)
{
//如果有右孩子,且右孩子的数值较大,则将右孩子的下标设置为largest
int largest = left + 1 < heapsize && a[left + 1] > a[left] ? left + 1 : left;
//比较根节点与较大孩子的数值,如果根节点大,则跳出循环
if (index1 == largest)
{
break;
}
//否则互换
swap(a, index1, largest);
//设置将最大值的下标赋值给index1,继续向下
index1 = largest;
left = 2 * index1 + 1;
}
}
void heapInsert(vector<int> &a, int index)
{
while (a[index] > a[(index - 1) / 2])
{
//两个元素互换
swap(a, a[index], a[(index - 1) / 2]);
//向上反馈
index = (index - 1) / 2;
}
}
void heapSort(vector<int> &a, int heapsize)
{
if (a.size() < 2)
return;
//将数组构建成大根堆
for (int i = heapsize-1; i >= 0; i--)
{
heapify(a, i, heapsize);
}
swap(a, 0, --heapsize);
while (heapsize>0)
{
//将变成大根堆的根节点与数组的最后一个数互换,并且将heapsize减小1
heapify(a, 0, heapsize);
swap(a, 0, --heapsize);
}
}
三、堆排序扩展
已知一个几乎有序的数组,几乎有序是指,如果把数组排好顺序的话,每个元素移动的距离可以不超过k,并且k相对于数组来说比较小。请选择一个合适的排序算法针对这个数据进行排序。
我们先构建一个元素数量为k的小根堆,因为移动距离最大为k,所以在极端情况下,使用这种方法将小根堆的根节点,也就是最小值放到0位置,然后指针向后移动一个位置,再将数组下表为k的元素放到小根堆内,再次组成一个小根堆,以此类推。最后将小根堆内的数依次从小到大弹出即可。
在c++中,multiset操作的底层就是二叉树的结构。
void SortArrayDistanceLessK(vector<int> &a, int k)
{
//定义一个multiset容器
multiset<int> s;
//设置遍历的起始点
int index = 0;
//防止k超过数组长度,要限制传入multiset容器的元素数量
int c = a.size();
int b = min(c, k);
for (; index <= b; index++)
{
//将数组的前K个数依次传到multiset容器中
s.insert(a[index]);
}
int i = 0;
//依次将K后面的元素传入multiset容器中,并弹出第一个元素
for (; index < a.size(); index++)
{
//将k之后的元素一个一个压入到multiset中
s.insert(a[index]);
//将set的第一个元素放到数组的第一个位置,并将multiset容器第一个元素删除
set<int>::const_iterator it = s.begin();
a[i] = *it;
//删除第一个元素
s.erase(s.begin());
i++;
}
//将multiset容器中的数据以此弹出
while (!s.empty())
{
//将set的第一个元素放到数组的第一个位置,并将multiset容器第一个元素删除
set<int>::const_iterator it = s.begin();
a[i++] = *it;
//删除第一个元素
s.erase(s.begin());
}
}
四、桶排序
基数排序:
c++代码示例
#include <cmath>
int getDigit(int x, int d)
{
//返回所需位数的数值
return((x / (int)pow(10, d - 1)) % 10);
}
//桶排序
void radixSort(vector<int> &a, int L, int R, int digit)
//L:要排序的左区域
//R:要排序的右区域
//digit十进制的位数
{
//以十为基底
int radix = 10;
int i = 0, j = 0;
//设置辅助空间,其大小与数组大小一致
int *bucket = new int[R - L + 1];
//有多少位就进出桶多少次,开始入桶
for (int d = 1; d <= digit; d++)
{
//count[0]为当前位(d位)是0的数字有多少个
//count[1]为当前位(d位)是0-1的数字有多少个
//count[2]为当前位(d位)是0-2的数字有多少个
//count[i]为当前位(d位)是0-i的数字有多少个
//申请一个辅助数组,记录上面的数据
int *count = new int[radix];
//将申请的内存全部附初值0
for (int i = 0; i < radix; i++)
{
count[i] = 0;
}
//开始入桶操作
for (i = L; i <=R; i++)
{
j = getDigit(a[i], d);
count[j]++;
}
//对辅助数组处理成前缀和
for (i = 1; i < radix; i++)
{
count[i] = count[i] + count[i - 1];
}
//开始出桶操作
for (i = R; i >= L; i--)
{
j = getDigit(a[i], d);
bucket[count[j] - 1] = a[i];
count[j]--;
}
int j = 0;
for (i = L; i <= R; i++)
{
a[i] = bucket[j];
j++;
}
}
}
int maxbits(vector<int> &a)
{
//定义一个最大数值暂存变量
int largest = 0;
for (int i = 0; i < a.size(); i++)
{
largest = max(largest, a[i]);
}
//开始计算最大数值的十进制数一共有多少位
int res = 0;
while (largest != 0)
{
res++;
largest /= 10;
}
return res;
}
void radixSort(vector<int> &a)
{
if (a.size() < 2)
return;
radixSort(a, 0, a.size() - 1, maxbits(a));
}
五、排序算法的稳定性及其汇总
同样值的个体之间,如果不因为排序而改变相对次序,就是这个排序是有稳定性的;否则就没有。
不具备稳定性的排序:
选择排序、快速排序、堆排序
具备稳定性的排序:
冒泡排序、插入排序、归并排序、一切桶排序思想下的排序
目前没有找到时间复杂度O(N*logN),额外空间复杂度0(1),又稳定的排序。
 注意!
注意!
1,归并排序的额外空间复杂度可以变成O(1),但是非常难,不需要掌握,有兴趣可以搜“归并排序内部缓存法”。
2,“原地归并排序”会让归并排序的时间复杂度变成o(N^2
)3,快速排序可以做到稳定性问题,但是非常难,不需要掌握,可以搜“01stable sort”
4,所有的改进都不重要,因为目前没有找到时间复杂度0(N*logN),额外空间复杂度0(1),又稳定的排序。
5,有一道题目,是奇数放在数组左边,偶数放在数组右边,还要求原始的相对次序不变,碰到这个问题,很难。