目录
1.问题的引出:
2.解决方案
<1>:自定义精度
<2>:系统提供的精度
3.总结
1.问题的引出:
浮点数在存储的时候,会存在精度的损失。
那么在浮点数进行比较的时候,可不可以使用 == 来进行比较,测试代码如下:
#include<stdio.h>
int main()
{
double a = 1.0;
double b = 0.1;
if ((a - 0.9) == 0.1)
{
printf("hahaha\n");
}
else
{
printf("hehehe\n");
}
return 0;
}在我们的认知里,a - 0.9 = 1.0-0.9 = 0.1 即程序运行成功后会输出 hahaha ,那么输出结果为是否为这样呢?
代码运行后的结果为:
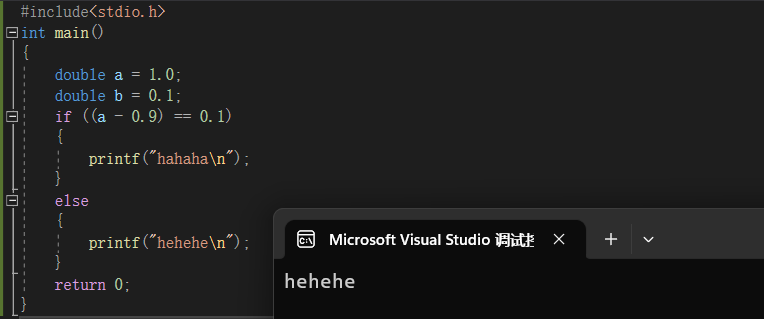
得出结论:浮点数在进行比较的时候,绝对不可以直接使用 == 来进行比较
为什么会产生上述结果呢?在此处我们将 a - 0.9 的值打印出来,同时为了更好更好地进行后续代码分析,我们将 0.1 的值也打印出来,代码为:
#include<stdio.h>
int main()
{
double a = 1.0;
double b = 0.1;
printf("%.50lf\n", a - 0.9);
printf("%.50lf\n", b);
//保留小数点后50位
return 0;
}
代码运行后的结果为:

在此处我们发现,与我们想象中的并不相同,a - 0.9 != 0.1,佐证了上述比较代码的真实性。
原因是,浮点数在存储的过程中存在精度损失,会导致结果存在细微的差别。
2.解决方案
<1>:自定义精度
在此处需要介绍一个函数 --- fabs (求绝对值函数)

我们可以自行定义一个精度,只要两浮点数相减的绝对值在我们定义的精度之内,我们就可以判定这两个浮点数相等。
对进行比较的代码稍作修改:
#include<stdio.h>
#include<math.h>
#define EPS 0.00000000000001
int main()
{
double a = 1.0;
double b = 0.1;
if (fabs((a - 0.9)-0.1) < EPS)
{
printf("hahaha\n");
}
else
{
printf("hehehe\n");
}
return 0;
}
程序运行的结果为:

我们可以看出,此时的输出结果为 hahaha ,不在为 hehehe 。
<2>:系统提供的精度
系统提供的精度为 --- DBL_EPSILON , 我们将其转到定义可以看到:
--- FLT_EPSILON


XXX_EPSILON 是最小误差 --- 即:XXX_EPSILON + n 不等于 n 的最小正数
有很多数字 + n 都可以不等于 n 但是 XXX_EPSILON 是最小的。
对比较的代码进行变化,得出下列代码:
#include<stdio.h>
#include<float.h>
#include<math.h>
int main()
{
double a = 1.0;
double b = 0.1;
if (fabs((a - 0.9) - 0.1) < FLT_EPSILON)
{
printf("hahaha\n");
}
else
{
printf("hehehe\n");
}
return 0;
}
运行结果为:
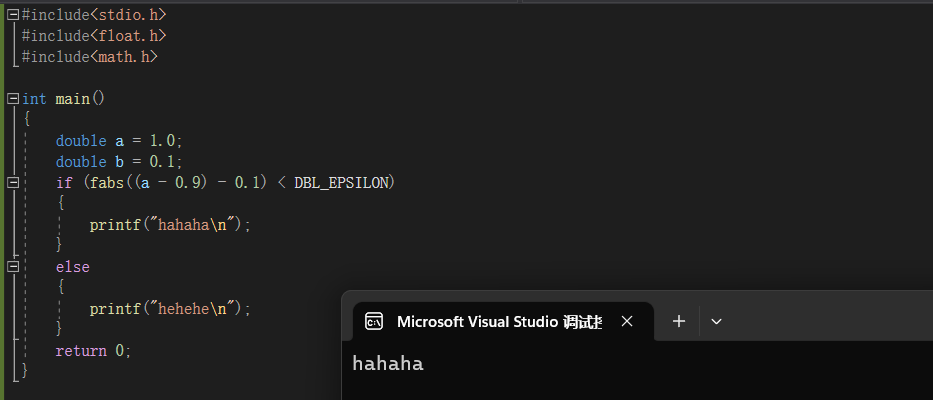
我们可以看出,此时的输出结果为 hahaha ,不在为 hehehe 。
3.总结
float 变量与 0 比较,只需要比较是否在精度范围内。
if (fabs((a - 0.9) - 0.1) < DBL_EPSILON) 可近似看作 if(fabs(x) < DBL_EPSILON)
思考,在此处是否可以改为 <= ???
fabs(x)=DBL_EPSILON;
即 double y + x != y; // x 为精度 --- 引起数据变化的最小值。
参考: 0 的定义 --- y + 0.0 = y;
我们可以得出,fabs(x) <= DBL_EPSILON(确认是否为0的逻辑),如果 = , 就说明 x 本身已经能够引起其他和它+-的数据本身的变化了,不符合0的概念。
不可以添加等号(=)。