图解LeetCode——114. 二叉树展开为链表

news2024/9/24 15:28:33

一、题目

给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。

展开后的单链表应该与二叉树 先序遍历 顺序相同。

二、示例

2.1> 示例 1：

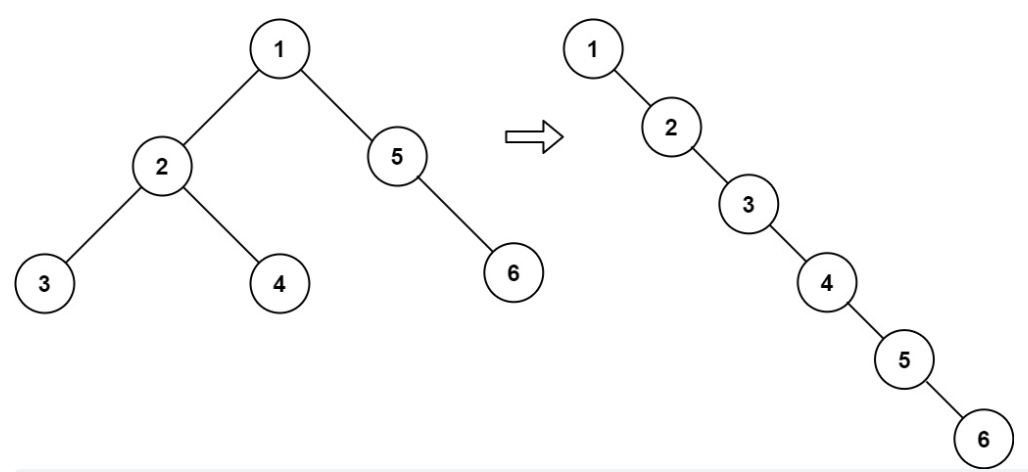
【输入】root = [1,2,5,3,4,null,6]
【输出】[1,null,2,null,3,null,4,null,5,null,6]

2.2> 示例 2：

【输入】root = []
【输出】[]

2.3> 示例 3：

【输入】root = [0]
【输出】[0]

提示：

树中结点数在范围 [0, 2000] 内
-100 <= Node.val <= 100

进阶：

你可以使用原地算法（O(1) 额外空间）展开这棵树吗？

三、解题思路

根据题目描述，需要我们根据给定的二叉树，然后对其进行先序遍历/前序遍历，从而拼装出一条链表。那么，首先我们先要弄清楚二叉树的遍历方式，我们以三个节点为例：node、leftNode和rightNode。遍历方式如下所示：

【前序遍历】node——>leftNode——>rightNode
【中序遍历】leftNode——>node——>rightNode
【后序遍历】leftNode——>rightNode——>node

那么，了解了先序遍历方式之后，就可以通过遍历一次二查树，将树节点TreeNode保存到List中，然后再针对List进行遍历操作，从而构造一条先序顺序的链表。

但是，我们从题目描述的“进阶”部分可以看到它的要求，即：你可以使用原地算法（O(1) 额外空间）展开这棵树吗？ 那么我们就不能使用List来进行TreeNode的存储了。我们此时就需要每当遍历一个树节点就进行一次链表拼装操作。那怎么操作呢?

【首先】创建两个指针，分别为遍历用的指针node，和指针node的前置指针preNode；
【其次】当preNode没有被初始化时，则preNode就指向node；
【第三】每当指针node遍历的下一个节点时，都是将preNode节点的right指向node节点，将preNode节点的left指向null；
【第四】preNode指针移动到node指针处，然后再重复第三步骤，直至整棵树遍历完毕；

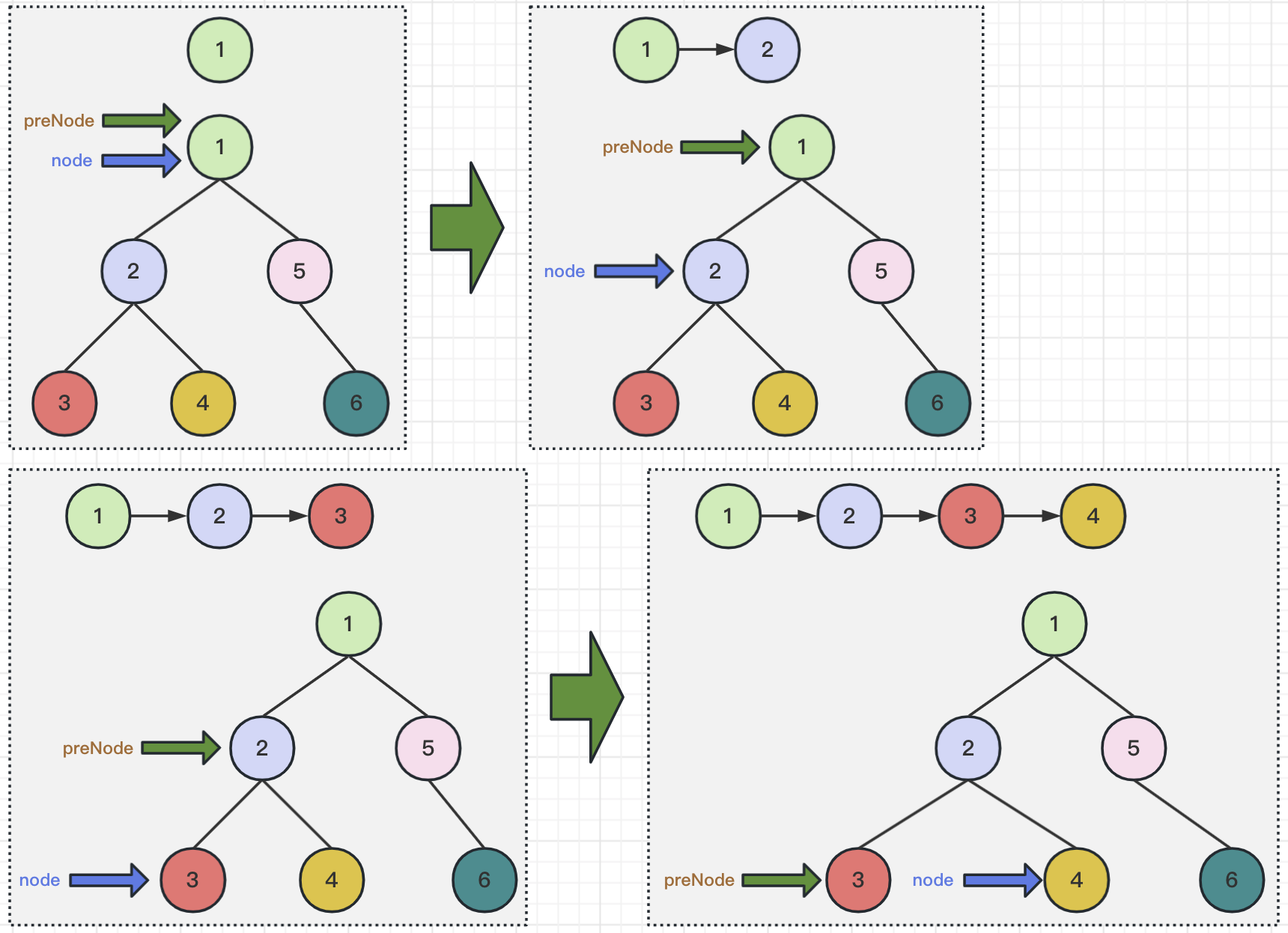
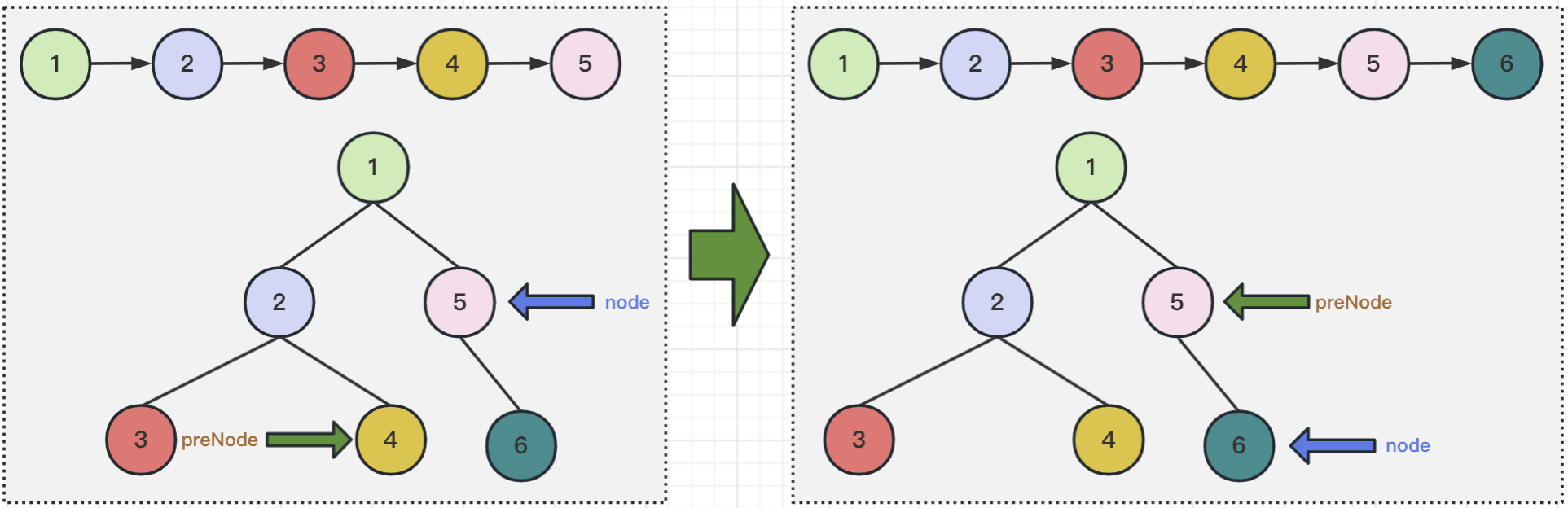
上面就是本题的解题思路，为了方便理解，下面我们以root = [1,2,5,3,4,null,6]为例，看一下具体的处理过程是怎么样的。请见下图所示：

四、代码实现

class Solution {
    TreeNode preNode;
    public void flatten(TreeNode root) {
        if (root == null) return;
        TreeNode leftNode = root.left;
        TreeNode rightNode = root.right;
        if (preNode == null) preNode = root;
        else {
            preNode.right = root;
            preNode.left = null;
            preNode = root;
        }
        flatten(leftNode);
        flatten(rightNode);
    }
}
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */