一、3D几何和参考系

1.旋转变换

旋转变换可以有很多方式来表示。 最常见的是使用旋转矩阵。

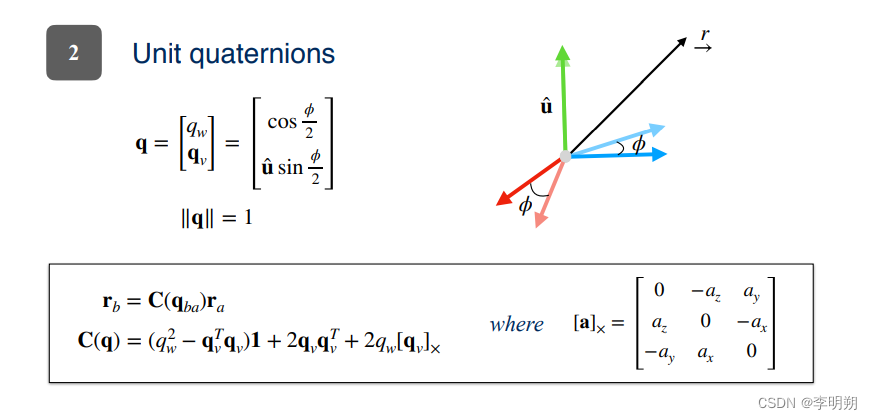
第二种表示方法就是使用单位四元数。单位四元数可以表示为单位长度的四维向量就足够了，这里有两个需要注意的东西，一是旋转轴 u ，二是旋转角度 ϕ。 四元数不受奇点的影响，与旋转矩阵相比它只需要四个参数而不是九个。

第三种表示方法就是使用欧拉角。欧拉角之所以有吸引力，原因在于它是一种直观简约的表示，只需要知道绕每个轴转动的角度就可以得到最终的旋转变换。

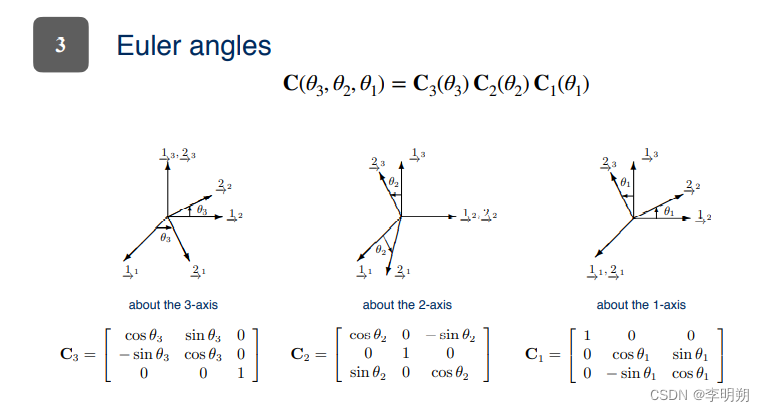
将三种方法对比，旋转矩阵可以表示任何旋转，但需要九个参数并有六个约束。单位四元数也可用于表示任何旋转，但它也有一个约束。 最后，欧拉角不受约束、直观地可视化并且仅需要三个参数，但受奇点影响。

2.参考系

车辆定位时将使用参考坐标系。

• 第一个坐标系是地心惯性坐标系(ECIF)。该坐标系的原点位于地球中心，z 轴指向正北，x 轴和 y 轴相对于非常遥远的恒星是固定的。 这意味着虽然地球绕 z 轴旋转，但 x 和 y 轴不会移动。
• 第一个坐标系是地心地球固定坐标系(ECEF)。与 ECIF 类似，只是它的 x 轴与本初子午线对齐并与地球一起旋转。y 轴由右手定则确定。ECEF坐标系是定位中经常用到的一个坐标系，主要是与GNSS传感器有关。
• 导航坐标系。一个常见的导航坐标系是选择某个位置作为起点并且坐标系与北、东和向下反向对齐的导航坐标系

二、惯性测量单元

惯性测量单元(IMU)测量物体在惯性空间中的运动。一般来说，惯性测量单元是一个复合传感器套件，它结合了三轴陀螺仪和三轴加速度计来跟踪刚体的外部自由运动。一些IMU还包含磁力计或指南针，以帮助跟踪方向。

1.陀螺仪

现代陀螺仪包含一个微机电系统，该系统由一个小的硅音叉组成，该系统根据施加的旋转或方向变化来改变其共振特性。它们测量旋转速率，而不是直接测量方向，因此必须对输出信号进行数值积分以确定方向变化。这个过程会在最终的方向估计中引入额外的误差。

其测量模型为
$$\omega (t)={\omega }_s(t)+b_{gyro}(t)+n_{gyro}(t)$$
其中${\omega }_s(t)$是陀螺仪测量值， 测量模型中包含一个缓慢变化的偏置项$b_{gyro}(t)$ 和一个白高斯加性噪声项$n_{gyro}(t)$来模拟传感器误差。

2.加速计

加速度计测量沿单个轴的加速度。当传感器加速时，光束发生偏转。可以通过电容电路测量这种偏转，并将其转换为加速度值。

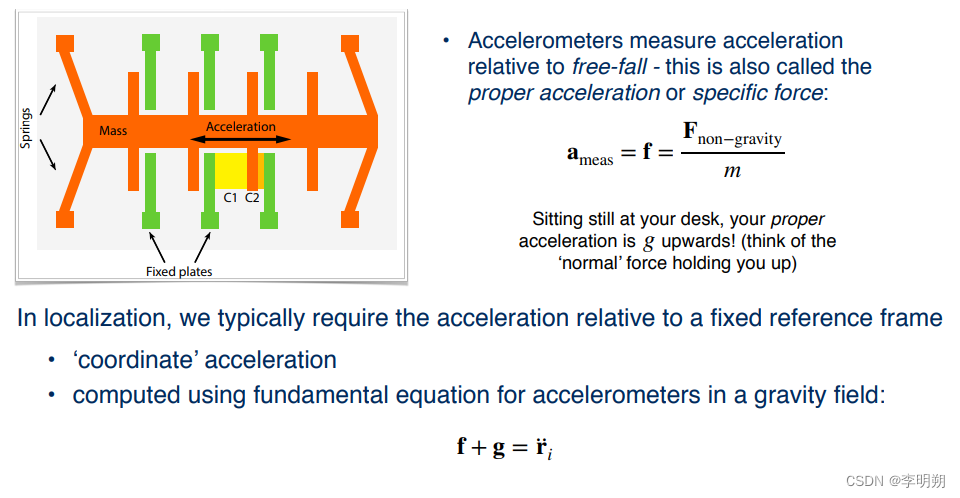
加速度计测量模型将具有类似的噪声和偏置项。但是现在，我们不再像使用旋转角速度那样直接测量身体加速度，而是需要使用重力场中加速度计的基本方程来消除重力的影响。公式如下：
$$a(t)=C_{sn}(t)({\ddot{r}}_n^{sn}(t)-g_n)+b_{accel}(t)+n_{accel}(t)$$
$C_{sn}(t)$为方向矩阵

IMU模型的一些限制：

• 首先，准确的方向估计对于准确的位置估计至关重要。 当我们将测得的比力转换为加速度时，我们必须确保重力方向是正确的。 否则，即使方向上的一个小错误也会让我们认为我们正在加速，而实际上我们并没有。
• 其次，我们推导出的两个模型都忽略了地球自转的影响。 对于更远距离的导航（飞机或导弹导航时不能忽略），这实际上很重要。
• 最后，我们推导出的模型适用于捷联IMU。 这些IMU是物理固定在车辆上，并且没有在万向节上安装旋转轮。 尽管后者可能更准确，但由于体积大且成本高，它们很少用于汽车应用。

三、全球导航卫星系统（GNSS）

GPS系统由位于六个轨道平面的 24-32 颗卫星组成。卫星会定期退役和更换。高度约为 20,000 公里，轨道周期不到 12 小时。系统的设计使得至少四颗卫星在地球上的任何表面点始终可见。

GPS背后的基本原理是到达时间测距。接收器通过将自己的内部时钟与传输时间的时钟进行比较来计算每个可见卫星的距离。使用电磁信号以光速传播的知识将时间差转换为距离。为了计算 3D 位置，测距方程需要至少四颗可见卫星。如果已知高度并且只需要 2D 位置，则只需要三颗卫星。

对于每颗卫星，伪距测量方程为：
$${\rho }^{(i)}=c(t_r-t_s)=\sqrt{(p^{(i)}-r{)}^T(p^{(i)}-r)}+c△t_r+c△t_n^{(i)}+{\eta }^{(i)}$$

GPS 存在多种误差源：

• 首先，电离层中的带电离子可以将信号延迟。
• 周围的地形和建筑物可能会引起反射，从而增加信号在到达接收器之前传播的距离，这些被称为多径误差。
• 时钟同步或卫星位置信息中的任何小错误都可能导致灾难性后果。即使是 1 微秒的计时误差也会导致 300 米的重大位置误差。星历数据和卫星时钟都会经常更新和重新校准，但校准可能会过时。
• 最后，可见卫星的几何配置也会导致定位精度的变化。这被称为精度的几何稀释。为了获得更高的精度，最好采用卫星遍布天空的配置。

我们可以通过以各种方式增强系统来提高GNSS精度。

• 差分GPS 可以通过使用一个或多个固定基站更准确的已知位置来校正接收机定位估计。修正以不同的频率广播到移动车辆中的 GNSS 接收器。
• 在某些情况下，实时动态或RTK GPS 利用载波相位信息将定位精度提高到两厘米。

四、激光雷达

1.激光雷达和测量模型

（1）激光雷达概述

LiDAR（激光雷达）可以感知到汽车四周所有方向并且能够提供非常准确的距离信息。如果要在一维空间中构建一个基本的 LIDAR，通常需要三个组件：一个激光器、一个光电探测器和一个非常精确的秒表。其原理是：

1. 激光器首先沿着一些已知的射线方向发射近红外频带内的短脉冲。与此同时，秒表开始计数。激光脉冲以光速从传感器向外行进并击中远距离目标。
2. 只要目标表面没有抛光或发亮，激光脉冲就会从目标表面向各个方向散射，其中一些反射光会沿着原始光线方向返回。光电探测器捕捉到返回脉冲，秒表会告诉你从脉冲第一次消失到它回来之间经过了多长时间。该时间称为往返时间
3. 将光速乘以往返时间来确定激光脉冲行进的总往返距离。

下图是一个原始的 LiDAR 扫描到的环境信息。中间的黑洞是传感器本身（激光雷达）所在的盲点，从那里向外扩散的同心圆是旋转的 Velodyne 传感器产生的扫描线。扫描中的每个点都根据返回信号的强度着色。 3D 扫描中的整个点集合称为点云（Point Clouds）

（2）测量模型

激光雷达通常使用球坐标 来表示单个点位置，我们使用r表示从激光雷达中心原点到 3D 点的距离，用ϵ表示从传感器 XY 平面向上或向下测量的俯仰角度，用α表示传感器 X 轴逆时针测量的方位角

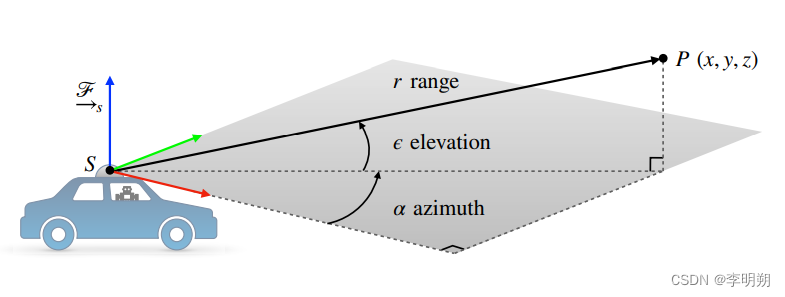
将球坐标转化为笛卡尔坐标，我们可以得到3D雷达和2D雷达的传感器模型以及逆传感器模型

3D LiDAR 的逆传感器模型为：
$$\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=h^{-1}(r,\alpha ,ϵ)\left[\begin{array}{c}r\cos \alpha \cos ϵ\\ r\sin \alpha \cos ϵ\\ r\sin ϵ\end{array}\right]$$
3D LiDAR 的前向传感器模型为：
$$\left[\begin{array}{c}r\\ \alpha \\ ϵ\end{array}\right]=h(x,y,z)\left[\begin{array}{c}\sqrt{x^2+y^2+z^2}\\ {\tan }^{-1}(\frac{y}{x})\\ {\sin }^{-1}(\frac{z}{\sqrt{x^2+y^2+z^2}})\end{array}\right]$$

2D LiDAR 的逆传感器模型为：
$$\left[\begin{array}{c}x\\ y\\ 0\end{array}\right]=h^{-1}(r,\alpha ,0)\left[\begin{array}{c}r\cos \alpha \\ r\sin \alpha \\ 0\end{array}\right]$$
2D LiDAR 的前向传感器模型为：
$$\left[\begin{array}{c}r\\ \alpha \\ 0\end{array}\right]=h(x,y,0)\left[\begin{array}{c}\sqrt{x^2+y^2}\\ {\tan }^{-1}(\frac{y}{x})\\ 0\end{array}\right]$$

对于激光雷达传感器，有几个重要的噪声源需要考虑。

• 反射信号到达的确切时间存在不确定性，这是因为我们用来计算飞行时间的秒表必然具有有限的分辨率
• 在 2D 和 3D 激光雷达中，方向的确切方向存在不确定性，因为用于测量的编码器也具有有限的分辨率
• 与目标表面的相互作用，它会减弱返回信号
• 光速实际上取决于它所穿过的材料。空气的温度和湿度也会突然影响光速。
• 运动失真，这是因为激光雷达所连接的车辆通常相对于它正在扫描的环境是运动的。

这些因素通常通过球坐标上的附加零均值高斯噪声来解释。 含有噪声的前向传感器模型为：
$$\left[\begin{array}{c}r\\ \alpha \\ ϵ\end{array}\right]=h(x,y,z)\left[\begin{array}{c}\sqrt{x^2+y^2+z^2}\\ {\tan }^{-1}(\frac{y}{x})\\ {\sin }^{-1}(\frac{z}{\sqrt{x^2+y^2+z^2}})\end{array}\right]+v,v\sim N(0,R)$$

2.点云

我们可以使用 LiDAR 扫描的所有测量值来构建点云。使用一个矩阵来存储点云数据，如下图所示

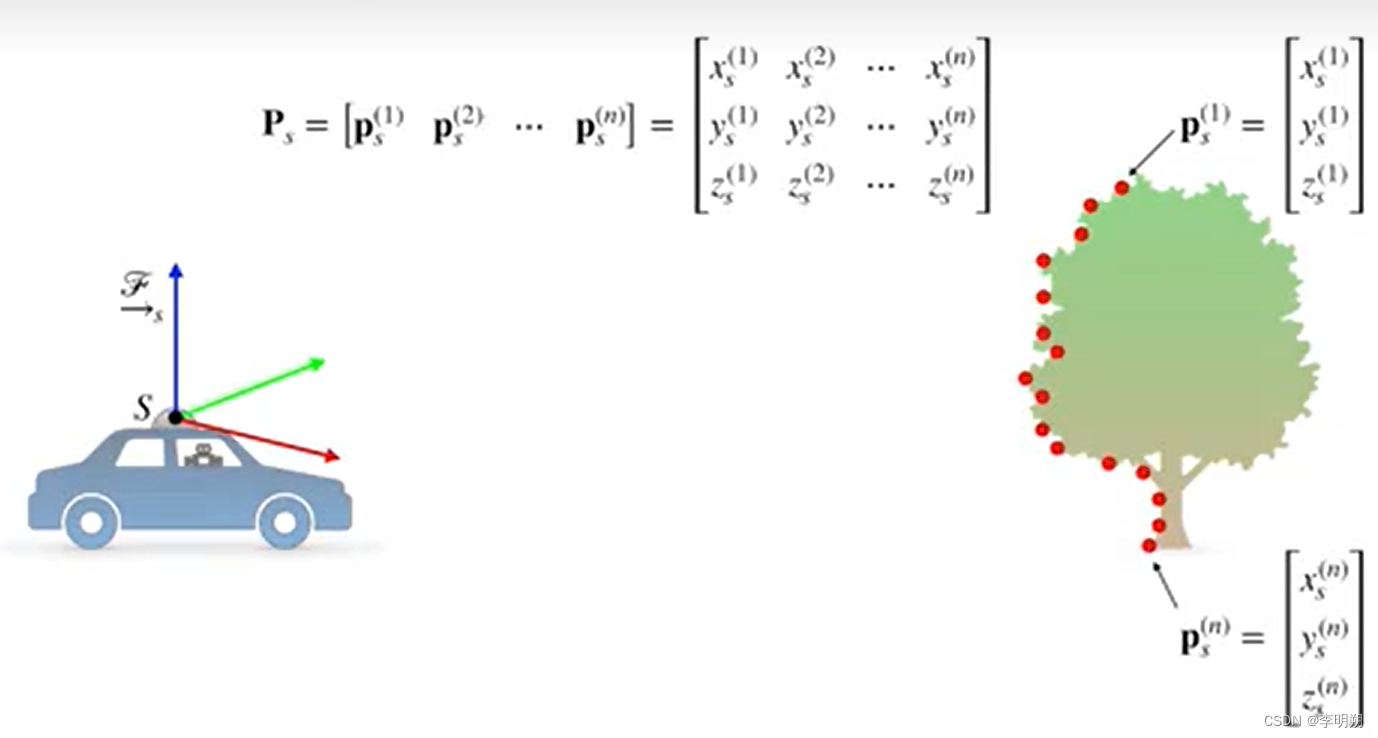
对于状态估计，世界上的物体大多保持不动，而车辆上的参考系一直在变并且从不同的角度观察世界。因此，我们考虑参考系的空间操作。点云有三个基本的空间操作：平移，旋转和缩放。

• 平移：
  
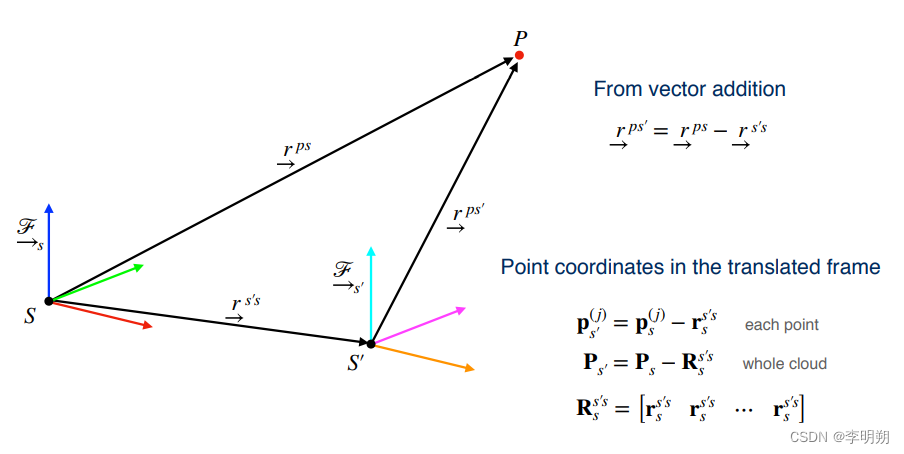
• 旋转
  
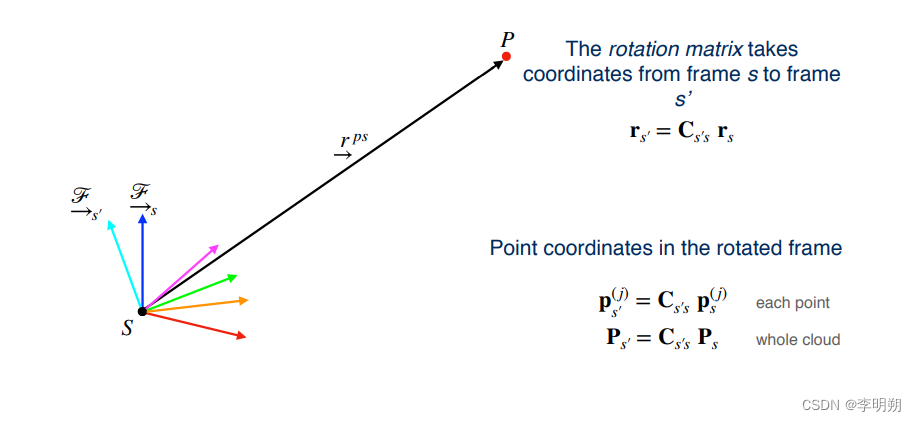
• 缩放
  
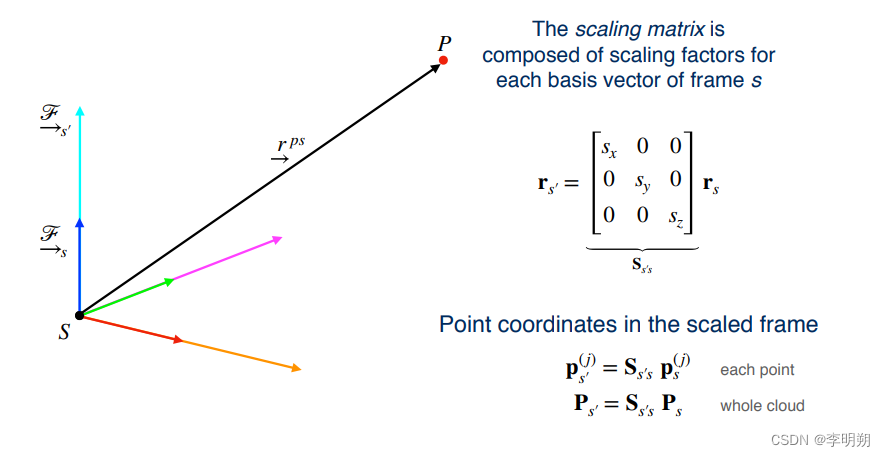
• 平移、旋转和缩放的组合
  

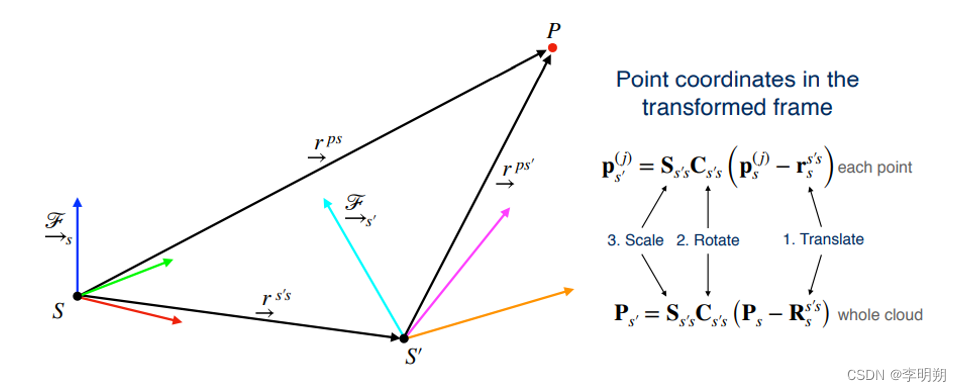
3.平面拟合

自动驾驶汽车的平面拟合的最常见和重要的应用之一确定路面的位置并预测汽车继续行驶时的位置。 3D平面等式为：
$$z=a+bx+cy$$
我们将会使用最小二乘法来根据雷达测量得到的x,y,x值来估计a,b,c

取平方误差函数关于参数向量 x xx 的偏导数，并将其设置为 0 以找到最小值，最终所要求的参数为：
$$\hat{x}=(A^{T}A{)}^{-1}{A}^{T}b$$

4.点云匹配

点云匹配问题是指同一物体在两个不同坐标系下的点云，如何去对齐两个点云并从而确定传感器在两帧之间的运动。解决这类问题最常用的算法称为迭代最近点算法或简称 ICP。

ICP 的思想是，我们对平移和旋转设定一个初始值$\left\{{\check{C}}_{s^{{}^{\prime }}s},{\check{r}}_s^{s^{{}^{\prime }}s}\right\}$ 然后对$P_{s^{{}^{\prime }}}$ 中的每一个点找到$P_s$中与它距离最近的点；然后求解最佳参数$\left\{{\hat{C}}_{s^{{}^{\prime }}s},{\hat{r}}_s^{s^{{}^{\prime }}s}\right\}$ 。以此类推，不停的迭代，直到最终收敛为止。

我们的目标是找到最能对齐两个点云的旋转和平移参数。 具体来说，我们希望使用最小二乘法最小化每对匹配点之间的距离平方之和，这是我们在此处定义的损失函数之一，公式为：
$$\left\{{\check{C}}_{s^{{}^{\prime }}s},{\check{r}}_s^{s^{{}^{\prime }}s}\right\}=argmin\left\{C_{s^{{}^{\prime }}},r_s^{s^{{}^{\prime }}}\right\}=argmin\sum _{j=1}^n{\Vert C_{s^{{}^{\prime }}s}(p_s^{(j)}-r_s^{s^{{}^{\prime }}s}-p_{s^{{}^{\prime }}}^{(j)})\Vert }_2^2$$
最优转换的方法，总共包含四步：

1. 计算每个点云的中心坐标，即所有点坐标求和取平均
2. 使用一个 矩阵来获取两个点云的分布。
   $$W_{s^{{}^{\prime }}s}=\frac{1}{n}\sum _{j=1}^n(p_s^{(j)}-{\mu }_s)(p_s^{(j)}-{\mu }_s{)}^T$$
3. 找到最佳旋转矩阵，通过对$W_{s^{{}^{\prime }}s}$进行奇异值分解得到旋转矩阵
4. 平移估计：将一个点云的中心旋转到另一个点云的参考系中，然后两个坐标向量的差即为平移向量。
   
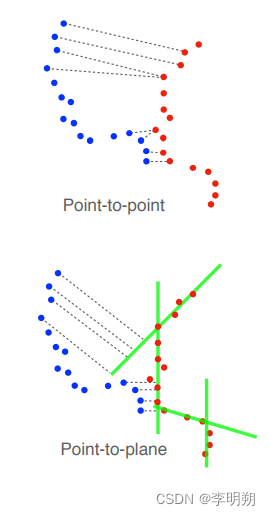
   上面介绍的算法只是 ICP 的一种变体，称为点对点 ICP，它的名字来源于我们的目标函数或损失函数最小化对应点对之间的距离。另一种在城市或室内等结构化环境使用的流行变体称为点到平面 ICP。我们不是最小化点对之间的距离，而是将多个平面拟合到第一个点云中，然后最小化第二个点云中的每个点与其最近的第一个点云中的平面之间的距离。
   

目前为止，我们一直假设我们的激光雷达看到的物体是静止的。但是在存在移动物体的情况下还继续使用 ICP 会使我们的运动估计远离真实运动。因此，我们需要小心排除或减轻违反我们对静止世界假设的异常点的影响。一种方法是将 ICP 运动估计与 GPS 和 INS 估计相结合。

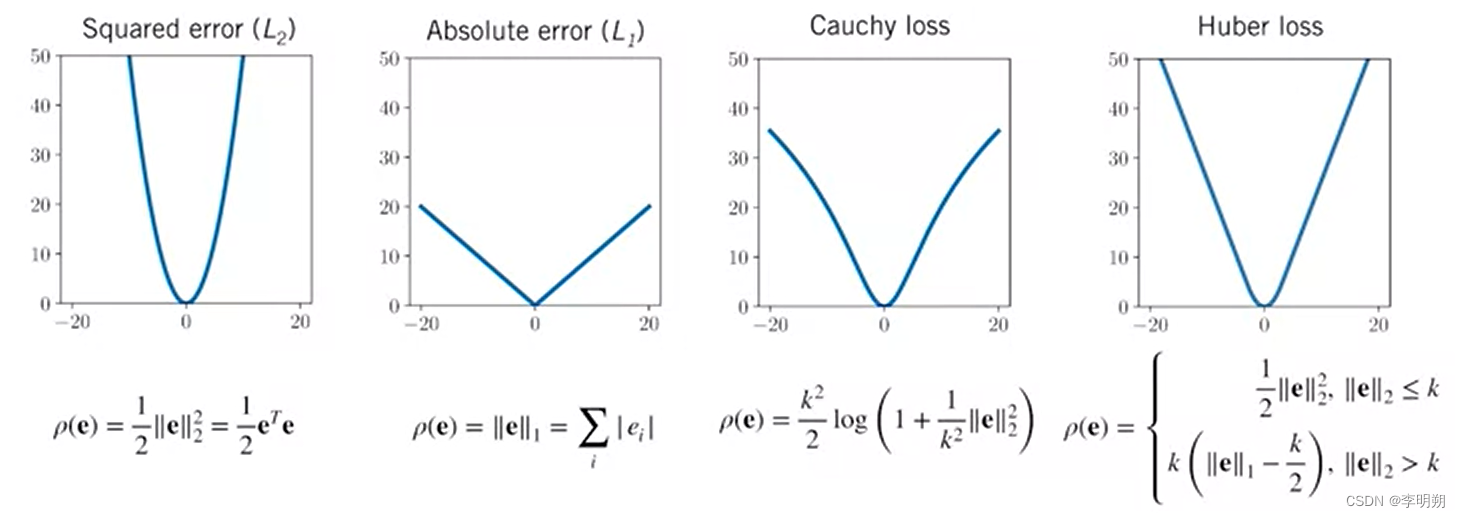
处理此类异常值的一种简单的方法是选择一个不同的损失函数，该损失函数对异常值引起的误差损失比我们的平方误差损失更不敏感。具有此属性的损失函数称为鲁棒损失函数或鲁棒成本函数，有多种选择。下图是常见的四种损失函数：