文章目录
- 三、卡尔曼滤波
- 1、随机系统状态空间模型
- 2、状态预测
- 3、状态量测
- 4、增益矩阵K与状态估计
- 5、Kalman滤波公式汇总
- 6、Kalman滤波流程图
- 1.划分为左右两部分(一阶矩和二阶矩)
- 2.划分为上下两部分(时间更新、量测更新)
- 7、Kalman滤波计算系统回路图
- 8、Kalman编程计算流程图
- 9、Kalman滤波特性
- 1.状态估计时量测的线性组合
- 2.正交投影性质
- 3.新息向量是零矩阵白噪声序列
- 10、带确定性输入的Kalman滤波
三、卡尔曼滤波
1、随机系统状态空间模型
{ X k = Φ k / k − 1 X k − 1 + Γ k − 1 W k − 1 Z k = H k X k + V k \left\{\begin{array}{l}\boldsymbol{X}_{k}=\boldsymbol{\Phi}_{k / k-1} \boldsymbol{X}_{k-1}+\boldsymbol{\Gamma}_{k-1} \boldsymbol{W}_{k-1} \\ \boldsymbol{Z}_{k}=\boldsymbol{H}_{k} \boldsymbol{X}_{k}+\boldsymbol{V}_{k}\end{array}\right. {Xk=Φk/k−1Xk−1+Γk−1Wk−1Zk=HkXk+Vk
关于噪声的基本假设:系统噪声 W k \boldsymbol{W}_{k} Wk 和量测噪声 V k \boldsymbol{V}_{k} Vk 都是零均值高斯白噪声,且不相关;系统噪声协方差阵 Q k \boldsymbol{Q}_{k} Qk 对称非负定,观测噪声协方差阵 R k \boldsymbol{R}_{k} Rk 对称正定。
- 其实改系统噪声前面系数 Γ k \Gamma_{k} Γk 可以使 Q k \boldsymbol{Q}_{k} Qk 总正定。
- 必须是高斯白噪声,多个高斯白噪声线性组合还是高斯白噪声,零均值均匀分布噪声线性组合不一定还是零均值均匀分布噪声。
{ E [ W k ] = 0 , E [ W k W j T ] = Q k δ k j E [ V k ] = 0 , E [ V k V j T ] = R k δ k j E [ W k V j T ] = 0 Q k ≥ 0 , R k > 0 ,或 Q k > 0 , R k > 0 \begin{array}{l}\left\{\begin{array}{l}\mathrm{E}\left[\boldsymbol{W}_{k}\right]=\mathbf{0}, \quad \mathrm{E}\left[\boldsymbol{W}_{k} \boldsymbol{W}_{j}^{\mathrm{T}}\right]=\boldsymbol{Q}_{k} \delta_{k j} \\ \mathrm{E}\left[\boldsymbol{V}_{k}\right]=\mathbf{0}, \quad \mathrm{E}\left[\boldsymbol{V}_{k} \boldsymbol{V}_{j}^{\mathrm{T}}\right]=\boldsymbol{R}_{k} \delta_{k j} \\ \mathrm{E}\left[\boldsymbol{W}_{k} \boldsymbol{V}_{j}^{\mathrm{T}}\right]=\mathbf{0}\end{array}\right. \\ \boldsymbol{Q}_{k} \geq 0, \quad \boldsymbol{R}_{k}>0,或\boldsymbol{Q}_{k} > 0, \quad \boldsymbol{R}_{k}>0 \end{array} ⎩ ⎨ ⎧E[Wk]=0,E[WkWjT]=QkδkjE[Vk]=0,E[VkVjT]=RkδkjE[WkVjT]=0Qk≥0,Rk>0,或Qk>0,Rk>0
2、状态预测
**状态一步预测:**预测下一时刻最有可能的那个值,由于高斯白噪声对状态预测的一阶矩不起作用(线性最小方差估计):
X
^
k
/
k
−
1
=
Φ
k
/
k
−
1
X
^
k
−
1
\hat{\boldsymbol{X}}_{k / k-1}={\boldsymbol{\Phi}}_{k / k-1} \hat{\boldsymbol{X}}_{k-1}
X^k/k−1=Φk/k−1X^k−1
状态预测误差:真值-预测
X
~
k
/
k
−
1
=
X
k
−
X
^
k
/
k
−
1
=
(
Φ
k
/
k
−
1
X
k
−
1
+
Γ
k
−
1
W
k
−
1
)
−
Φ
k
/
k
−
1
X
^
k
−
1
=
Φ
k
/
k
−
1
(
X
k
−
1
−
X
^
k
−
1
)
+
Γ
k
−
1
W
k
−
1
=
Φ
k
/
k
−
1
X
~
k
−
1
+
Γ
k
−
1
W
k
−
1
\begin{array}{r}\tilde{\boldsymbol{X}}_{k / k-1}=\boldsymbol{X}_{k}-\hat{\boldsymbol{X}}_{k / k-1}=\left(\boldsymbol{\Phi}_{k / k-1} \boldsymbol{X}_{k-1}+\boldsymbol{\Gamma}_{k-1} \boldsymbol{W}_{k-1}\right)-\boldsymbol{\Phi}_{k / k-1} \hat{\boldsymbol{X}}_{k-1} \\ \quad=\boldsymbol{\Phi}_{k / k-1}\left(\boldsymbol{X}_{k-1}-\hat{\boldsymbol{X}}_{k-1}\right)+\boldsymbol{\Gamma}_{k-1} \boldsymbol{W}_{k-1}=\boldsymbol{\Phi}_{k / k-1} \tilde{\boldsymbol{X}}_{k-1}+\boldsymbol{\Gamma}_{k-1} \boldsymbol{W}_{k-1}\end{array}
X~k/k−1=Xk−X^k/k−1=(Φk/k−1Xk−1+Γk−1Wk−1)−Φk/k−1X^k−1=Φk/k−1(Xk−1−X^k−1)+Γk−1Wk−1=Φk/k−1X~k−1+Γk−1Wk−1
状态预测方差阵:一步预测误差相乘的期望,乘出来有四项,由于两时刻噪声不相关,其中两项为0。所以预测的方差就是上一时刻的方差传递过来
Φ
k
/
k
−
1
P
k
−
1
Φ
k
/
k
−
1
T
\boldsymbol{\Phi}_{k / k-1} \boldsymbol{P}_{k-1} \boldsymbol{\Phi}_{k / k-1}^{\mathrm{T}}
Φk/k−1Pk−1Φk/k−1T,加上当前误差
Γ
k
−
1
Q
k
−
1
Γ
k
−
1
T
\boldsymbol{\Gamma}_{k-1} \boldsymbol{Q}_{k-1} \boldsymbol{\Gamma}_{k-1}^{\mathrm{T}}
Γk−1Qk−1Γk−1T
P
k
/
k
−
1
=
E
[
X
~
k
/
k
−
1
X
~
k
/
k
−
1
T
]
=
E
[
(
Φ
k
/
k
−
1
X
~
k
−
1
+
Γ
k
−
1
W
k
−
1
)
(
Φ
k
/
k
−
1
X
~
k
−
1
+
Γ
k
−
1
W
k
−
1
)
T
]
=
Φ
k
/
k
−
1
E
[
X
~
k
−
1
X
~
k
−
1
T
]
Φ
k
/
k
−
1
T
+
Γ
k
−
1
E
[
W
k
−
1
W
k
−
1
T
]
Γ
k
−
1
T
=
Φ
k
/
k
−
1
P
k
−
1
Φ
k
/
k
−
1
T
+
Γ
k
−
1
Q
k
−
1
Γ
k
−
1
T
\begin{aligned} \boldsymbol{P}_{k / k-1} & =\mathrm{E}\left[\tilde{\boldsymbol{X}}_{k / k-1} \tilde{\boldsymbol{X}}_{k / k-1}^{\mathrm{T}}\right] \\ & =\mathrm{E}\left[\left(\boldsymbol{\Phi}_{k / k-1} \tilde{\boldsymbol{X}}_{k-1}+\boldsymbol{\Gamma}_{k-1} \boldsymbol{W}_{k-1}\right)\left(\boldsymbol{\Phi}_{k / k-1} \tilde{\boldsymbol{X}}_{k-1}+\boldsymbol{\Gamma}_{k-1} \boldsymbol{W}_{k-1}\right)^{\mathrm{T}}\right] \\ & =\boldsymbol{\Phi}_{k / k-1} \mathrm{E}\left[\tilde{\boldsymbol{X}}_{k-1} \tilde{\boldsymbol{X}}_{k-1}^{\mathrm{T}}\right] \boldsymbol{\Phi}_{k / k-1}^{\mathrm{T}}+\boldsymbol{\Gamma}_{k-1} \mathrm{E}\left[\boldsymbol{W}_{k-1} \boldsymbol{W}_{k-1}^{\mathrm{T}}\right] \boldsymbol{\Gamma}_{k-1}^{\mathrm{T}} \\ & =\boldsymbol{\Phi}_{k / k-1} \boldsymbol{P}_{k-1} \boldsymbol{\Phi}_{k / k-1}^{\mathrm{T}}+\boldsymbol{\Gamma}_{k-1} \boldsymbol{Q}_{k-1} \boldsymbol{\Gamma}_{k-1}^{\mathrm{T}} \end{aligned}
Pk/k−1=E[X~k/k−1X~k/k−1T]=E[(Φk/k−1X~k−1+Γk−1Wk−1)(Φk/k−1X~k−1+Γk−1Wk−1)T]=Φk/k−1E[X~k−1X~k−1T]Φk/k−1T+Γk−1E[Wk−1Wk−1T]Γk−1T=Φk/k−1Pk−1Φk/k−1T+Γk−1Qk−1Γk−1T
3、状态量测
量测:量测值带入量测方程,同样忽略高斯白噪声的影响:
Z
^
k
/
k
−
1
=
H
k
X
^
k
/
k
−
1
\hat{\boldsymbol{Z}}_{k / k-1}=\boldsymbol{H}_{k} \hat{\boldsymbol{X}}_{k / k-1}
Z^k/k−1=HkX^k/k−1
量测误差:
Z
~
k
/
k
−
1
=
Z
k
−
Z
^
k
/
k
−
1
=
(
H
k
X
k
+
V
k
)
−
H
k
X
^
k
/
k
−
1
=
H
k
X
~
k
/
k
−
1
+
V
k
\begin{aligned} \tilde{\boldsymbol{Z}}_{k / k-1} & =\boldsymbol{Z}_{k}-\hat{\boldsymbol{Z}}_{k / k-1}=\left(\boldsymbol{H}_{k} \boldsymbol{X}_{k}+\boldsymbol{V}_{k}\right)-\boldsymbol{H}_{k} \hat{\boldsymbol{X}}_{k / k-1} =\boldsymbol{H}_{k} \tilde{\boldsymbol{X}}_{k / k-1}+\boldsymbol{V}_{k}\end{aligned}
Z~k/k−1=Zk−Z^k/k−1=(HkXk+Vk)−HkX^k/k−1=HkX~k/k−1+Vk
量测方差阵:
P
Z
Z
,
k
/
k
−
1
=
E
[
Z
~
k
/
k
−
1
Z
~
k
/
k
−
1
T
]
=
E
[
(
H
k
X
~
k
/
k
−
1
+
V
k
)
(
H
k
X
~
k
/
k
−
1
+
V
k
)
T
]
=
H
k
E
[
X
~
k
/
k
−
1
X
~
k
/
k
−
1
T
]
H
k
T
+
E
[
V
k
V
k
T
]
=
H
k
P
k
/
k
−
1
H
k
T
+
R
k
\begin{aligned} \boldsymbol{P}_{Z Z, k / k-1} & =\mathrm{E}\left[\tilde{\boldsymbol{Z}}_{k / k-1} \tilde{\boldsymbol{Z}}_{k / k-1}^{\mathrm{T}}\right] \\ & =\mathrm{E}\left[\left(\boldsymbol{H}_{k} \tilde{\boldsymbol{X}}_{k / k-1}+\boldsymbol{V}_{k}\right)\left(\boldsymbol{H}_{k} \tilde{\boldsymbol{X}}_{k / k-1}+\boldsymbol{V}_{k}\right)^{\mathrm{T}}\right] \\ & =\boldsymbol{H}_{k} \mathrm{E}\left[\tilde{\boldsymbol{X}}_{k / k-1} \tilde{\boldsymbol{X}}_{k / k-1}^{\mathrm{T}}\right] \boldsymbol{H}_{k}^{\mathrm{T}}+\mathrm{E}\left[\boldsymbol{V}_{k} \boldsymbol{V}_{k}^{\mathrm{T}}\right] \\ & =\boldsymbol{H}_{k} \boldsymbol{P}_{k / k-1} \boldsymbol{H}_{k}^{\mathrm{T}}+\boldsymbol{R}_{k}\end{aligned}
PZZ,k/k−1=E[Z~k/k−1Z~k/k−1T]=E[(HkX~k/k−1+Vk)(HkX~k/k−1+Vk)T]=HkE[X~k/k−1X~k/k−1T]HkT+E[VkVkT]=HkPk/k−1HkT+Rk
量测互协方差:X 与 Z 之间,状态的一步预测误差和量测之间的互协方差
一般不为0,为0就没有滤波的必要了
P X Z , k / k − 1 = E [ X ~ k / k − 1 Z ~ k / k − 1 T ] = E [ X ~ k / k − 1 ( H k X ~ k / k − 1 + V k ) T ] = P k / k − 1 H k T \begin{array}{l}\boldsymbol{P}_{X Z, k / k-1}=\mathrm{E}\left[\tilde{\boldsymbol{X}}_{k / k-1} \tilde{\boldsymbol{Z}}_{k / k-1}^{\mathrm{T}}\right] \\ \quad=\mathrm{E}\left[\tilde{\boldsymbol{X}}_{k / k-1}\left(\boldsymbol{H}_{k} \tilde{\boldsymbol{X}}_{k / k-1}+\boldsymbol{V}_{k}\right)^{\mathrm{T}}\right] \\ \quad=\boldsymbol{P}_{k / k-1} \boldsymbol{H}_{k}^{\mathrm{T}}\end{array} PXZ,k/k−1=E[X~k/k−1Z~k/k−1T]=E[X~k/k−1(HkX~k/k−1+Vk)T]=Pk/k−1HkT
4、增益矩阵K与状态估计
假设滤波方程可以写成 状态预测+K量测修正 形式,
K
{\color{red}K}
K 矩阵先待定
状态估计:
X
^
k
=
X
^
k
/
k
−
1
+
K
k
Z
k
~
=
X
^
k
/
k
−
1
+
K
k
(
Z
k
−
H
k
X
^
k
/
k
−
1
)
\hat{\boldsymbol{X}}_{k}=\hat{\boldsymbol{X}}_{k / k-1}+{\color{red}\boldsymbol{K}_{k} }\tilde{{\boldsymbol{Z}}_{k}}=\hat{\boldsymbol{X}}_{k / k-1}+{\color{red}\boldsymbol{K}_{k}}\left(\boldsymbol{Z}_{k}-\boldsymbol{H}_{k} \hat{\boldsymbol{X}}_{k / k-1}\right)
X^k=X^k/k−1+KkZk~=X^k/k−1+Kk(Zk−HkX^k/k−1)
状态估计误差:
X
~
k
=
X
k
−
X
^
k
=
X
k
−
[
X
^
k
/
k
−
1
+
K
k
(
Z
k
−
H
k
X
^
k
/
k
−
1
)
]
=
X
~
k
/
k
−
1
−
K
k
(
H
k
X
k
+
V
k
−
H
k
X
^
k
/
k
−
1
)
=
(
I
−
K
k
H
k
)
X
~
k
/
k
−
1
−
K
k
V
k
\begin{aligned} \tilde{\boldsymbol{X}}_{k} & =\boldsymbol{X}_{k}-\hat{\boldsymbol{X}}_{k}=\boldsymbol{X}_{k}-\left[\hat{\boldsymbol{X}}_{k / k-1}+{\color{red}\boldsymbol{K}_{k}}\left(\boldsymbol{Z}_{k}-\boldsymbol{H}_{k} \hat{\boldsymbol{X}}_{k / k-1}\right)\right] \\ & =\tilde{\boldsymbol{X}}_{k / k-1}-{\color{red}\boldsymbol{K}_{k}}\left(\boldsymbol{H}_{k} \boldsymbol{X}_{k}+\boldsymbol{V}_{k}-\boldsymbol{H}_{k} \hat{\boldsymbol{X}}_{k / k-1}\right)=\left(\boldsymbol{I}-\boldsymbol{K}_{k} \boldsymbol{H}_{k}\right) \tilde{\boldsymbol{X}}_{k / k-1}-{\color{red}\boldsymbol{K}_{k}} \boldsymbol{V}_{k}\end{aligned}
X~k=Xk−X^k=Xk−[X^k/k−1+Kk(Zk−HkX^k/k−1)]=X~k/k−1−Kk(HkXk+Vk−HkX^k/k−1)=(I−KkHk)X~k/k−1−KkVk
状态估计方差阵:
P
k
=
E
[
X
~
k
X
~
k
T
]
=
E
{
[
(
I
−
K
k
H
k
)
X
~
k
/
k
−
1
−
K
k
V
k
]
[
(
I
−
K
k
H
k
)
X
~
k
/
k
−
1
−
K
k
V
k
]
T
}
=
(
I
−
K
k
H
k
)
E
[
X
~
k
/
k
−
1
X
~
k
/
k
−
1
T
]
(
I
−
K
k
H
k
)
T
+
K
k
E
[
V
k
V
k
T
]
K
k
T
=
(
I
−
K
k
H
k
)
P
k
/
k
−
1
(
I
−
K
k
H
k
)
T
+
K
k
R
k
K
k
T
\begin{aligned} \boldsymbol{P}_{k} &= \mathrm{E}\left[\tilde{\boldsymbol{X}}_{k} \tilde{\boldsymbol{X}}_{k}^{\mathrm{T}}\right] \\ & =\mathrm{E}\left\{\left[\left(\boldsymbol{I}-{\color{red}\boldsymbol{K}_{k}} \boldsymbol{H}_{k}\right) \tilde{\boldsymbol{X}}_{k / k-1}-{\color{red}\boldsymbol{K}_{k}} \boldsymbol{V}_{k}\right]\left[\left(\boldsymbol{I}-\boldsymbol{K}_{k} \boldsymbol{H}_{k}\right) \tilde{\boldsymbol{X}}_{k / k-1}-{\color{red}\boldsymbol{K}_{k} }\boldsymbol{V}_{k}\right]^{\mathrm{T}}\right\} \\ & =\left(\boldsymbol{I}-{\color{red}\boldsymbol{K}_{k}}\boldsymbol{H}_{k}\right) \mathrm{E}\left[\tilde{\boldsymbol{X}}_{k / k-1} \tilde{\boldsymbol{X}}_{k / k-1}^{\mathrm{T}}\right]\left(\boldsymbol{I}-{\color{red}\boldsymbol{K}_{k}} \boldsymbol{H}_{k}\right)^{\mathrm{T}}+{\color{red}\boldsymbol{K}_{k}} \mathrm{E}\left[\boldsymbol{V}_{k} \boldsymbol{V}_{k}^{\mathrm{T}}\right] {\color{red}\boldsymbol{K}_{k}^{\mathrm{T}}} \\ & =\left(\boldsymbol{I}-{\color{red}\boldsymbol{K}_{k}} \boldsymbol{H}_{k}\right) \boldsymbol{P}_{k / k-1}\left(\boldsymbol{I}-{\color{red}\boldsymbol{K}_{k}} \boldsymbol{H}_{k}\right)^{\mathrm{T}}+{\color{red}\boldsymbol{K}_{k}} \boldsymbol{R}_{k} {\color{red}\boldsymbol{K}_{k}^{\mathrm{T}}}\end{aligned}
Pk=E[X~kX~kT]=E{[(I−KkHk)X~k/k−1−KkVk][(I−KkHk)X~k/k−1−KkVk]T}=(I−KkHk)E[X~k/k−1X~k/k−1T](I−KkHk)T+KkE[VkVkT]KkT=(I−KkHk)Pk/k−1(I−KkHk)T+KkRkKkT
到此,都是假设,在待定
K
{\color{red}K}
K 的情况下进行状态预测,并算出方差阵,下面就是要求
K
{\color{red}K}
K :
K {\color{red}K} K 矩阵可以取某个值,使状态估计方差 P k \boldsymbol{P}_{k} Pk 达到最小,且保持 P k \boldsymbol{P}_{k} Pk 对称正定。
要理解矩阵最小的含义,得先理解 A A A 矩阵小于 B B B 矩阵的含义: B − A B-A B−A 正定
由最优估计的含义可知,等价于求
P
k
\boldsymbol{P}_{k}
Pk 的迹,最小,先展开:
P
k
=
(
I
−
K
k
H
k
)
P
k
/
k
−
1
(
I
−
K
k
H
k
)
T
+
K
k
R
k
K
k
T
=
P
k
/
k
−
1
−
K
k
H
k
P
k
/
k
−
1
−
(
K
k
H
k
P
k
/
k
−
1
)
T
+
K
k
(
H
k
P
k
/
k
−
1
H
k
T
+
R
k
)
K
k
T
\begin{aligned} \boldsymbol{P}_{k} & =\left(\boldsymbol{I}-\boldsymbol{K}_{k} \boldsymbol{H}_{k}\right) \boldsymbol{P}_{k / k-1}\left(\boldsymbol{I}-\boldsymbol{K}_{k} \boldsymbol{H}_{k}\right)^{\mathrm{T}}+\boldsymbol{K}_{k} \boldsymbol{R}_{k} \boldsymbol{K}_{k}^{\mathrm{T}} \\ & =\boldsymbol{P}_{k / k-1}-\boldsymbol{K}_{k} \boldsymbol{H}_{k} \boldsymbol{P}_{k / k-1}-\left(\boldsymbol{K}_{k} \boldsymbol{H}_{k} \boldsymbol{P}_{k / k-1}\right)^{\mathrm{T}}+\boldsymbol{K}_{k}\left(\boldsymbol{H}_{k} \boldsymbol{P}_{k / k-1} \boldsymbol{H}_{k}^{\mathrm{T}}+\boldsymbol{R}_{k}\right) \boldsymbol{K}_{k}^{\mathrm{T}}\end{aligned}
Pk=(I−KkHk)Pk/k−1(I−KkHk)T+KkRkKkT=Pk/k−1−KkHkPk/k−1−(KkHkPk/k−1)T+Kk(HkPk/k−1HkT+Rk)KkT
再求迹,分解开,就是一个单输入多输出的多元函数:
tr
(
P
k
)
=
tr
(
P
k
/
k
−
1
)
−
tr
(
K
k
H
k
P
k
/
k
−
1
)
−
tr
(
(
K
k
H
k
P
k
/
k
−
1
)
T
)
+
tr
(
K
k
(
H
k
P
k
/
k
−
1
H
k
T
+
R
k
)
K
k
T
)
\begin{aligned} \operatorname{tr}\left(\boldsymbol{P}_{k}\right)= & \operatorname{tr}\left(\boldsymbol{P}_{k / k-1}\right)-\operatorname{tr}\left(\boldsymbol{K}_{k} \boldsymbol{H}_{k} \boldsymbol{P}_{k / k-1}\right) \\ & -\operatorname{tr}\left(\left(\boldsymbol{K}_{k} \boldsymbol{H}_{k} \boldsymbol{P}_{k / k-1}\right)^{\mathrm{T}}\right)+\operatorname{tr}\left(\boldsymbol{K}_{k}\left(\boldsymbol{H}_{k} \boldsymbol{P}_{k / k-1} \boldsymbol{H}_{k}^{\mathrm{T}}+\boldsymbol{R}_{k}\right) \boldsymbol{K}_{k}^{\mathrm{T}}\right)\end{aligned}
tr(Pk)=tr(Pk/k−1)−tr(KkHkPk/k−1)−tr((KkHkPk/k−1)T)+tr(Kk(HkPk/k−1HkT+Rk)KkT)
要求多元函数的极值,就是找求导等于
0
0
0 的点,由求导规则:
d
d
X
[
tr
(
X
B
)
]
=
d
d
X
[
tr
(
(
X
B
)
T
)
]
=
B
T
d
d
X
[
tr
(
X
A
X
T
)
]
=
2
X
A
,
A
为对称阵时
\begin{array}{l}\frac{\mathrm{d}}{\mathrm{d} \boldsymbol{X}}[\operatorname{tr}(\boldsymbol{X} \boldsymbol{B})]=\frac{\mathrm{d}}{\mathrm{d} \boldsymbol{X}}\left[\operatorname{tr}\left((\boldsymbol{X} \boldsymbol{B})^{\mathrm{T}}\right)\right]=\boldsymbol{B}^{\mathrm{T}} \\ \frac{\mathrm{d}}{\mathrm{d} \boldsymbol{X}}\left[\operatorname{tr}\left(\boldsymbol{X} \boldsymbol{A} \boldsymbol{X}^{\mathrm{T}}\right)\right]=2 \boldsymbol{X} \boldsymbol{A},A为对称阵时\end{array}
dXd[tr(XB)]=dXd[tr((XB)T)]=BTdXd[tr(XAXT)]=2XA,A为对称阵时
求导得:
d
d
K
k
[
tr
(
P
k
)
]
=
0
−
(
H
k
P
k
/
k
−
1
)
T
−
(
H
k
P
k
/
k
−
1
)
T
+
2
K
k
(
H
k
P
k
/
k
−
1
H
k
T
+
R
k
)
=
0
\frac{\mathrm{d}}{\mathrm{d} \boldsymbol{K}_{k}}\left[\operatorname{tr}\left(\boldsymbol{P}_{k}\right)\right]=\mathbf{0}{\color{green}-\left(\boldsymbol{H}_{k} \boldsymbol{P}_{k / k-1}\right)^{\mathrm{T}}-\left(\boldsymbol{H}_{k} \boldsymbol{P}_{k / k-1}\right)^{\mathrm{T}}}+2 {\color{red}\boldsymbol{K}_{k}}\left(\boldsymbol{H}_{k} \boldsymbol{P}_{k / k-1} \boldsymbol{H}_{k}^{\mathrm{T}}+\boldsymbol{R}_{k}\right)=\mathbf{0}
dKkd[tr(Pk)]=0−(HkPk/k−1)T−(HkPk/k−1)T+2Kk(HkPk/k−1HkT+Rk)=0
绿色的部分为移到左边,两边除以 2 得:
P
k
/
k
−
1
H
k
T
=
K
k
(
H
k
P
k
/
k
−
1
H
k
T
+
R
k
)
\boldsymbol{P}_{k / k-1} \boldsymbol{H}_{k}^{\mathrm{T}}={\color{red}\boldsymbol{K}_{k}}\left(\boldsymbol{H}_{k} \boldsymbol{P}_{k / k-1} \boldsymbol{H}_{k}^{\mathrm{T}}+\boldsymbol{R}_{k}\right)
Pk/k−1HkT=Kk(HkPk/k−1HkT+Rk)
要求出 K {\color{red}K} K ,需要 K {\color{red}K} K 后面部分可逆,即量测噪声 R k \boldsymbol{R}_{k} Rk 要正定;前面的 H k P k / k − 1 H k \boldsymbol{H}_{k} \boldsymbol{P}_{k / k-1} \boldsymbol{H}_{k} HkPk/k−1Hk 由于 H k \boldsymbol{H}_{k} Hk 有很多 0 0 0 元素,可逆会不正定,如果加上一个总是正定 R k \boldsymbol{R}_{k} Rk,还能维持整体的正定,继续求逆。
K
{\color{red}K}
K 后面部分可逆乘到两边:
K
k
=
P
k
/
k
−
1
H
k
T
(
H
k
P
k
/
k
−
1
H
k
T
+
R
k
)
−
1
{\color{red}\boldsymbol{K}_{k}}=\boldsymbol{P}_{k / k-1} \boldsymbol{H}_{k}^{\mathrm{T}}\left(\boldsymbol{H}_{k} \boldsymbol{P}_{k / k-1} \boldsymbol{H}_{k}^{\mathrm{T}}+\boldsymbol{R}_{k}\right)^{-1}
Kk=Pk/k−1HkT(HkPk/k−1HkT+Rk)−1
将求出的增益矩阵
K
K
K 带回到最上面状态估计和方差的的方程中,得出Kalman滤波解。
消除一部分元素,可以得到短一些的方差: P k = ( I − K k H k ) P k / k − 1 \boldsymbol{P}_{k}=\left(\boldsymbol{I}-\boldsymbol{K}_{k} \boldsymbol{H}_{k}\right) \boldsymbol{P}_{k / k-1} Pk=(I−KkHk)Pk/k−1
5、Kalman滤波公式汇总
-
状态一步预测: X ^ k ∣ k − 1 = Φ k ∣ k − 1 X ^ k − 1 \hat{\boldsymbol{X}}_{k \mid k-1}=\boldsymbol{\Phi}_{k \mid k-1} \hat{\boldsymbol{X}}_{k-1} X^k∣k−1=Φk∣k−1X^k−1
-
状态一步预测均方误差: P k / k − 1 = Φ k / k − 1 P k − 1 Φ k / k − 1 T + Γ k − 1 Q k − 1 Γ k − 1 T \boldsymbol{P}_{k / k-1}=\boldsymbol{\Phi}_{k / k-1} \boldsymbol{P}_{k-1} \boldsymbol{\Phi}_{k / k-1}^{\mathrm{T}}+\boldsymbol{\Gamma}_{k-1} \boldsymbol{Q}_{k-1} \boldsymbol{\Gamma}_{k-1}^{\mathrm{T}} Pk/k−1=Φk/k−1Pk−1Φk/k−1T+Γk−1Qk−1Γk−1T
-
滤波增益: K k = P k / k − 1 H k T ( H k P k / k − 1 H k T + R k ) − 1 \boldsymbol{K}_{k}=\boldsymbol{P}_{k / k-1} \boldsymbol{H}_{k}^{\mathrm{T}}\left(\boldsymbol{H}_{k} \boldsymbol{P}_{k / k-1} \boldsymbol{H}_{k}^{\mathrm{T}}+\boldsymbol{R}_{k}\right)^{-1} Kk=Pk/k−1HkT(HkPk/k−1HkT+Rk)−1
-
状态估计: X ^ k = X ^ k / k − 1 + K k ( Z k − H k X ^ k / k − 1 ) \hat{\boldsymbol{X}}_{k}=\hat{\boldsymbol{X}}_{k / k-1}+\boldsymbol{K}_{k}\left(\boldsymbol{Z}_{k}-\boldsymbol{H}_{k} \hat{\boldsymbol{X}}_{k / k-1}\right) X^k=X^k/k−1+Kk(Zk−HkX^k/k−1)
-
状态估计均方误差: P k = ( I − K k H k ) P k / k − 1 \boldsymbol{P}_{k}=\left(\boldsymbol{I}-\boldsymbol{K}_{k} \boldsymbol{H}_{k}\right) \boldsymbol{P}_{k / k-1} Pk=(I−KkHk)Pk/k−1
6、Kalman滤波流程图
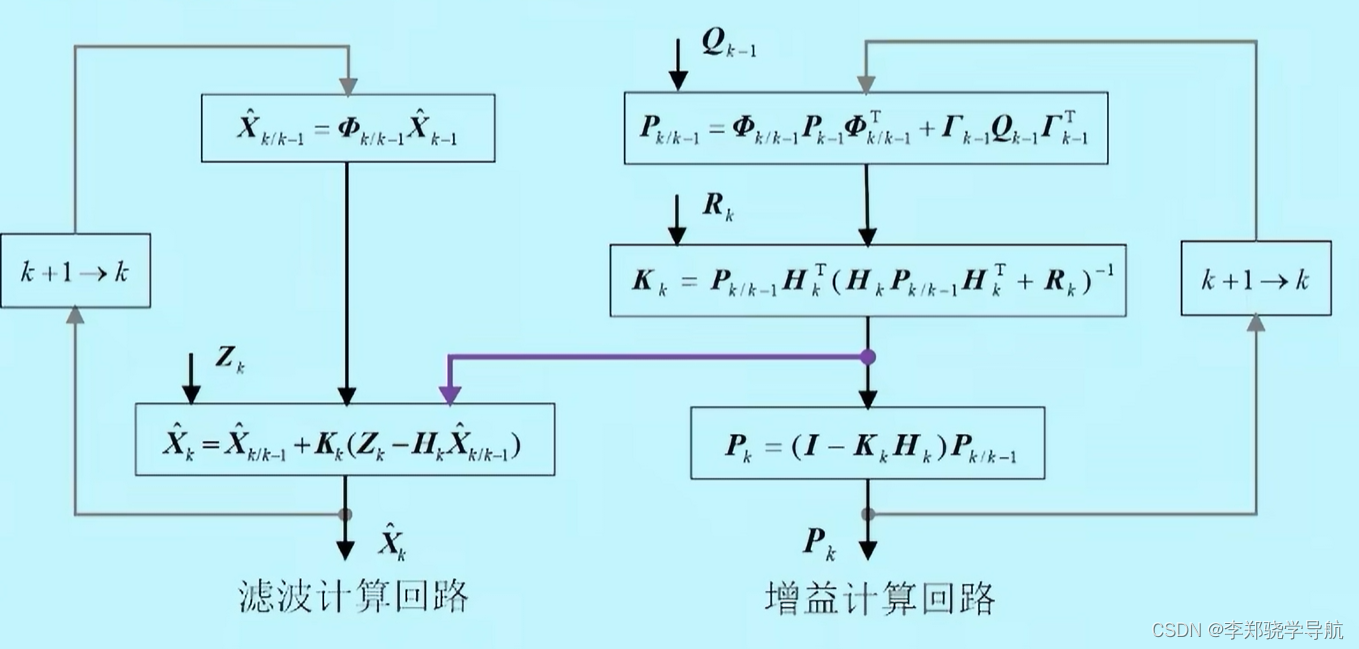
1.划分为左右两部分(一阶矩和二阶矩)
- 左边一部分滤波计算回路是一阶矩的更新过程,
- 右边增益计算回路是二阶矩的更新
- 左边对右边没有影响,右边通过增益矩阵对左边产生影响。有时候数组不好左边计算都崩溃了,对右边都没有影响,还按照模型来计算
2.划分为上下两部分(时间更新、量测更新)
- 上面是时间更新,之和状态方程有关系。
- 下面是量测更新,只和量测方程有关系。
7、Kalman滤波计算系统回路图

- 总的来说,是一个线性系统,输入 Z k Z_{k} Zk,输出 X ^ k \hat{{X}}_{k} X^k
- 右边部分是时间更新,以系统上一时刻的输出为输入,输出当前时刻的预测状态
- 左边部分是量测更新
- Kalman滤波对线性系统来说,是最小方差线性无偏估计
8、Kalman编程计算流程图
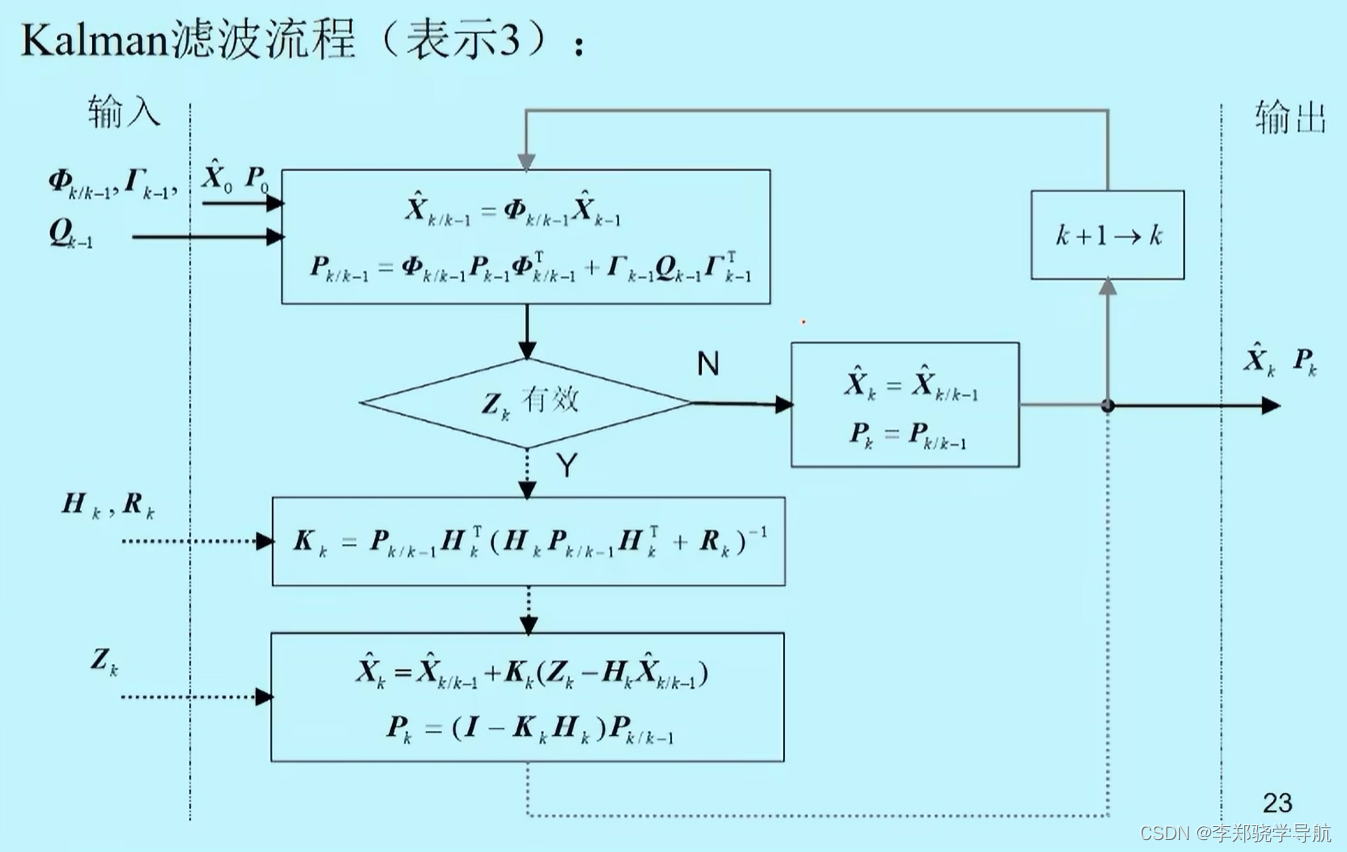
- 如果不是定常系统, Φ k / k − 1 , Γ k − 1 \boldsymbol{\Phi}_{k / k-1}, \boldsymbol{\Gamma}_{k-1} Φk/k−1,Γk−1, Q k − 1 \boldsymbol{Q}_{k-1} Qk−1, H k , R k \boldsymbol{H}_{k}, \boldsymbol{R}_{k} Hk,Rk 都是时变的,需要给出;定常系统作为常数就行。
- 如果系统非线性,是高阶系统,必须给出初始状态 X ^ 0 , P 0 \hat{\boldsymbol{X}}_{0} ,\boldsymbol{P}_{0} X^0,P0
- 输出一阶矩、二阶矩
- 一阶矩、二阶矩能代表系统的全部,随机信号需要时正态分布的
- 二阶矩是为了下一时刻计算权重(增益矩阵 K K K)
- 量测更新和时间更新可能不同步;常见的是量测更新频率小于时间更新频率。
9、Kalman滤波特性
1.状态估计时量测的线性组合
Kalman滤波是一种递推的公式,,上一时刻可以递推当前时刻,不断递推。以预测和量测加权的方式表示:
X
^
k
=
X
^
k
/
k
−
1
+
K
k
(
Z
k
−
H
k
X
^
k
/
k
−
1
)
=
(
I
−
K
k
H
k
)
Φ
k
/
k
−
1
X
^
k
−
1
+
K
k
Z
k
=
G
k
X
^
k
−
1
+
K
k
Z
k
=
G
k
(
G
k
−
1
X
^
k
−
2
+
K
k
−
1
Z
k
−
1
)
+
K
k
Z
k
=
G
k
G
k
−
1
X
^
k
−
2
+
G
k
K
k
−
1
Z
k
−
1
+
K
k
Z
k
=
G
k
G
k
−
1
G
k
−
2
X
^
k
−
3
+
G
k
G
k
−
1
K
k
−
2
Z
k
−
2
+
G
k
K
k
−
1
Z
k
−
1
+
K
k
Z
k
=
⋯
=
(
∏
i
=
1
k
G
i
)
X
^
0
+
∑
i
=
1
k
(
∏
j
=
i
+
1
k
G
j
)
K
i
Z
i
\begin{aligned} \hat{\boldsymbol{X}}_{k} & =\hat{\boldsymbol{X}}_{k / k-1}+\boldsymbol{K}_{k}\left(\boldsymbol{Z}_{k}-\boldsymbol{H}_{k} \hat{\boldsymbol{X}}_{k / k-1}\right) \\ & =\left(\boldsymbol{I}-\boldsymbol{K}_{k} \boldsymbol{H}_{k}\right) \boldsymbol{\Phi}_{k / k-1} \hat{\boldsymbol{X}}_{k-1}+\boldsymbol{K}_{k} \boldsymbol{Z}_{k}=\boldsymbol{G}_{k} \hat{\boldsymbol{X}}_{k-1}+\boldsymbol{K}_{k} \boldsymbol{Z}_{k} \\ & =\boldsymbol{G}_{k}\left(\boldsymbol{G}_{k-1} \hat{\boldsymbol{X}}_{k-2}+\boldsymbol{K}_{k-1} \boldsymbol{Z}_{k-1}\right)+\boldsymbol{K}_{k} \boldsymbol{Z}_{k} \\ & =\boldsymbol{G}_{k} \boldsymbol{G}_{k-1} \hat{\boldsymbol{X}}_{k-2}+\boldsymbol{G}_{k} \boldsymbol{K}_{k-1} \boldsymbol{Z}_{k-1}+\boldsymbol{K}_{k} \boldsymbol{Z}_{k} \\ & =\boldsymbol{G}_{k} \boldsymbol{G}_{k-1} \boldsymbol{G}_{k-2} \hat{\boldsymbol{X}}_{k-3}+\boldsymbol{G}_{k} \boldsymbol{G}_{k-1} \boldsymbol{K}_{k-2} \boldsymbol{Z}_{k-2}+\boldsymbol{G}_{k} \boldsymbol{K}_{k-1} \boldsymbol{Z}_{k-1}+\boldsymbol{K}_{k} \boldsymbol{Z}_{k} \\ & =\cdots \\ & =\left(\prod_{i=1}^{k} \boldsymbol{G}_{i}\right) \hat{\boldsymbol{X}}_{0}+\sum_{i=1}^{k}\left(\prod_{j=i+1}^{k} \boldsymbol{G}_{j}\right) \boldsymbol{K}_{i} \boldsymbol{Z}_{i}\end{aligned}
X^k=X^k/k−1+Kk(Zk−HkX^k/k−1)=(I−KkHk)Φk/k−1X^k−1+KkZk=GkX^k−1+KkZk=Gk(Gk−1X^k−2+Kk−1Zk−1)+KkZk=GkGk−1X^k−2+GkKk−1Zk−1+KkZk=GkGk−1Gk−2X^k−3+GkGk−1Kk−2Zk−2+GkKk−1Zk−1+KkZk=⋯=(i=1∏kGi)X^0+i=1∑k(j=i+1∏kGj)KiZi
如果初值
X
^
0
\hat{\boldsymbol{X}}_{0}
X^0 取值
0
0
0 ,当前的估计值就是前面所有量测值
Z
i
\boldsymbol{Z_i}
Zi 的线性组合
2.正交投影性质
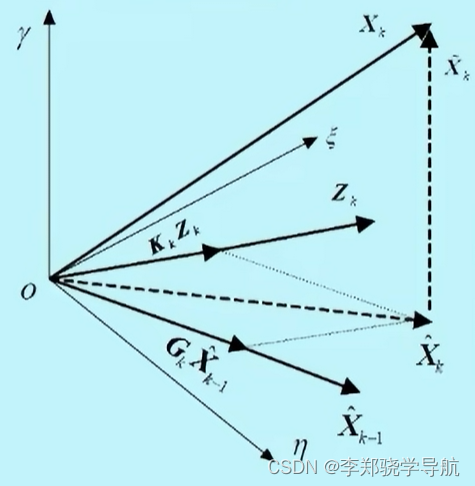
- Kalman滤波估计就是预测和量测的加权平均。
- 量测是一条矢量、预测也是一条矢量,前面乘上加权系数再相加。
- 无论前面系数是多少,相加得到的估计值都在同一个平面上。
- 真实的状态也是空间中一条矢量。
- 要使估计值和真值直接的误差最小,即在平面上取到平面外一点距离最小的点,就是取正交投影点。
3.新息向量是零矩阵白噪声序列
{ E [ Z ~ k / k − 1 ] = 0 E [ Z ~ k / k − 1 Z ~ j / j − 1 T ] = ( H k P k / k − 1 H k T + R k ) δ k j \left\{\begin{array}{l}\mathrm{E}\left[\tilde{\boldsymbol{Z}}_{k / k-1}\right]=\mathbf{0} \\ \mathrm{E}\left[\tilde{\boldsymbol{Z}}_{k / k-1} \tilde{\boldsymbol{Z}}_{j / j-1}^{\mathrm{T}}\right]=\left(\boldsymbol{H}_{k} \boldsymbol{P}_{k / k-1} \boldsymbol{H}_{k}^{\mathrm{T}}+\boldsymbol{R}_{k}\right) \delta_{k j}\end{array}\right. ⎩ ⎨ ⎧E[Z~k/k−1]=0E[Z~k/k−1Z~j/j−1T]=(HkPk/k−1HkT+Rk)δkj
10、带确定性输入的Kalman滤波
状态空间模型:
{
X
k
=
Φ
k
/
k
−
1
X
k
−
1
+
B
k
−
1
u
k
−
1
+
Γ
k
−
1
W
k
−
1
Z
k
=
H
k
X
k
+
Y
k
+
V
k
\left\{\begin{array}{l}\boldsymbol{X}_{k}=\boldsymbol{\Phi}_{k / k-1} \boldsymbol{X}_{k-1}+{\color{red}\boldsymbol{B}_{k-1} \boldsymbol{u}_{k-1}}+\boldsymbol{\Gamma}_{k-1} \boldsymbol{W}_{k-1} \\ \boldsymbol{Z}_{k}=\boldsymbol{H}_{k} \boldsymbol{X}_{k}+{\color{red}\boldsymbol{Y}_{k}}+\boldsymbol{V}_{k}\end{array}\right.
{Xk=Φk/k−1Xk−1+Bk−1uk−1+Γk−1Wk−1Zk=HkXk+Yk+Vk
滤波方程,只有和一阶矩有关的部分需要改动:
{
X
^
k
/
k
−
1
=
Φ
k
/
k
−
1
X
^
k
−
1
+
B
k
−
1
u
k
−
1
P
k
/
k
−
1
=
Φ
k
/
k
−
1
P
k
−
1
Φ
k
/
k
−
1
T
+
Γ
k
−
1
Q
k
−
1
Γ
k
−
1
T
K
k
=
P
k
/
k
−
1
H
k
T
(
H
k
P
k
/
k
−
1
H
k
T
+
R
k
)
−
1
X
^
k
=
X
^
k
/
k
−
1
+
K
k
(
Z
k
−
Y
k
−
H
k
X
^
k
/
k
−
1
)
P
k
=
(
I
−
K
k
H
k
)
P
k
/
k
−
1
\left\{\begin{array}{l}\hat{\boldsymbol{X}}_{k / k-1}=\boldsymbol{\Phi}_{k / k-1} \hat{\boldsymbol{X}}_{k-1}+{\color{red}\boldsymbol{B}_{k-1} \boldsymbol{u}_{k-1}} \\ \boldsymbol{P}_{k / k-1}=\boldsymbol{\Phi}_{k / k-1} \boldsymbol{P}_{k-1} \boldsymbol{\Phi}_{k / k-1}^{\mathrm{T}}+\boldsymbol{\Gamma}_{k-1} \boldsymbol{Q}_{k-1} \boldsymbol{\Gamma}_{k-1}^{\mathrm{T}} \\ \boldsymbol{K}_{k}=\boldsymbol{P}_{k / k-1} \boldsymbol{H}_{k}^{\mathrm{T}}\left(\boldsymbol{H}_{k} \boldsymbol{P}_{k / k-1} \boldsymbol{H}_{k}^{\mathrm{T}}+\boldsymbol{R}_{k}\right)^{-1} \\ \hat{\boldsymbol{X}}_{k}=\hat{\boldsymbol{X}}_{k / k-1}+\boldsymbol{K}_{k}\left(\boldsymbol{Z}_{k}-{\color{red}\boldsymbol{Y}_{k}}-\boldsymbol{H}_{k} \hat{\boldsymbol{X}}_{k / k-1}\right) \\ \boldsymbol{P}_{k}=\left(\boldsymbol{I}-\boldsymbol{K}_{k} \boldsymbol{H}_{k}\right) \boldsymbol{P}_{k / k-1}\end{array}\right.
⎩
⎨
⎧X^k/k−1=Φk/k−1X^k−1+Bk−1uk−1Pk/k−1=Φk/k−1Pk−1Φk/k−1T+Γk−1Qk−1Γk−1TKk=Pk/k−1HkT(HkPk/k−1HkT+Rk)−1X^k=X^k/k−1+Kk(Zk−Yk−HkX^k/k−1)Pk=(I−KkHk)Pk/k−1





![使用RP2040自制的树莓派pico—— [1/100] 烧录micropython固件](https://img-blog.csdnimg.cn/81186a1aba7c4ea5974964ef2707035e.png)