练习3：多分类问题

---

介绍

在本练习中，我们将使用逻辑回归来识别手写数字（0到9）。我们将扩展在练习2中对逻辑回归的实现，并将其应用于一对多的分类问题。

在开始练习前，需要下载如下的文件进行数据上传：

• ex3data1.mat -手写数字训练集

在整个练习中，涉及如下的必做作业：

• 实现逻辑回归向量化----(40分)
• 训练一对多的多分类器----(40分)
• 使用多分类器进行预测----(20分)

1 多分类

在本部分练习中，你需要扩展之前实现的逻辑回归算法，将其应用于多分类问题。

1.1 数据集

文件ex3data1.mat中的数据包含5000个手写数字的训练集。其中每个样本是20像素x20像素的灰度图像，每个像素由一个浮点数表示，代表该位置的灰度强度。
将20x20的像素网格展开成400维向量，则每个训练样本变成了数据矩阵中的一行向量。如下图所示，该文件给了我们一个5000x400的矩阵，其中每行都是手写数字图像的样本。

训练集的第二部分是包含训练集标签的5000维向量$y$。

1.2 数据可视化

图像在矩阵X中表示为400维向量（其中有5,000个）。 400维“特征”是原始20 x 20图像中每个像素的灰度强度。类标签在向量y中作为表示图像中数字的数字类。

接下来，我们需要加载数据。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.io import loadmat

data = loadmat('/home/jovyan/work/ex3data1.mat')
data

{'__header__': b'MATLAB 5.0 MAT-file, Platform: GLNXA64, Created on: Sun Oct 16 13:09:09 2011',
 '__version__': '1.0',
 '__globals__': [],
 'X': array([[0., 0., 0., ..., 0., 0., 0.],
        [0., 0., 0., ..., 0., 0., 0.],
        [0., 0., 0., ..., 0., 0., 0.],
        ...,
        [0., 0., 0., ..., 0., 0., 0.],
        [0., 0., 0., ..., 0., 0., 0.],
        [0., 0., 0., ..., 0., 0., 0.]]),
 'y': array([[10],
        [10],
        [10],
        ...,
        [ 9],
        [ 9],
        [ 9]], dtype=uint8)}

并使用shape内置函数检查数据矩阵$X$,$y$的形状：

data['X'].shape, data['y'].shape

((5000, 400), (5000, 1))

1.3 逻辑回归的向量化

在该部分练习中，你需要将逻辑回归的实现修改为完全向量化（即没有可替换的$for$循环）。这是因为向量化代码除了简洁外，还能够利用线性代数优化，并且通常比迭代代码快得多。但是，如果从练习2中看到我们的代价函数已经完全向量化实现了，所以我们可以在这里重复使用相同的实现。

1.3.1 代价函数的向量化

你需要编写代码实现代价函数的向量化。我们已经知道，代价函数是：

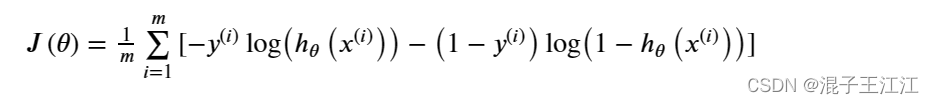
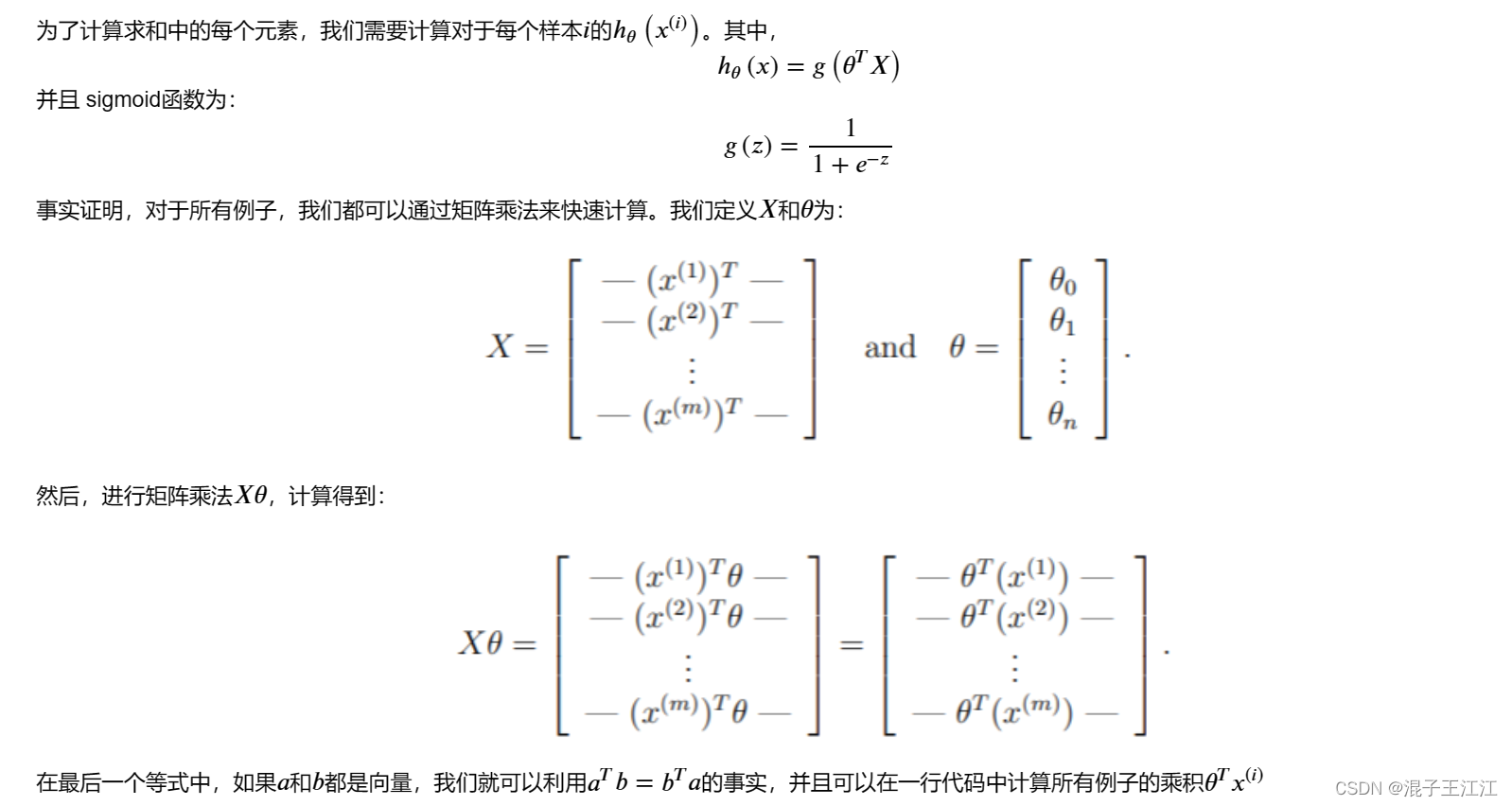
###在这里填入代码###
def sigmoid(z):
    return 1 / (1 + np.exp(-z))

def cost(theta, X, y):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
    second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T))) 
    return np.sum(first - second) / len(X)

1.3.2 梯度的向量化

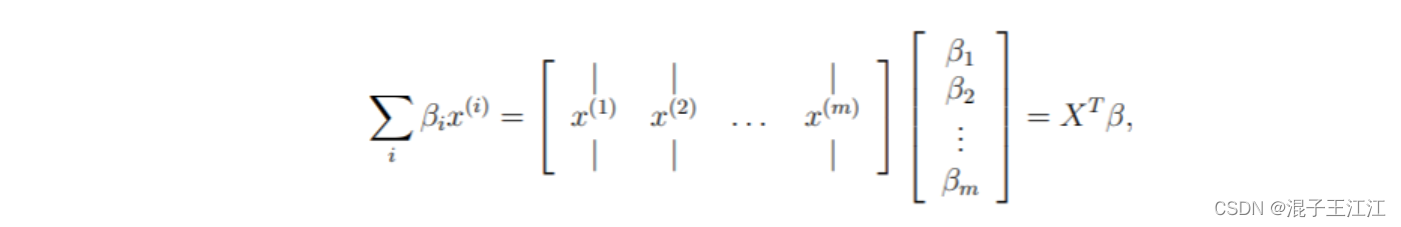
在对操作进行向量化之后，我们知道可以不需要使用LOOP循环就可以进行偏导的计算。接下来你需要编写代码实现上述代码的向量化形式。

###在这里填入代码###
def gradient(theta, X, y):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    
    parameters = int(theta.ravel().shape[1])
    error = sigmoid(X * theta.T) - y
    
    grad = ((X.T * error) / len(X)).T
    
    return grad

1.3.3 正则化逻辑回归的向量化

在练习2中，我们实现正则化逻辑回归算法的代价函数和梯度计算函数。其代价函数为：

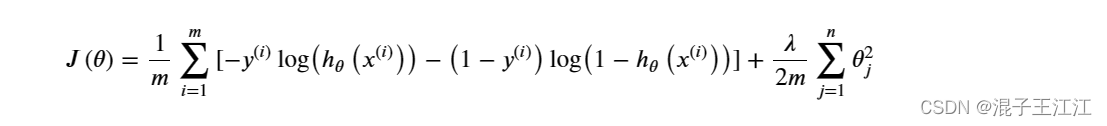
注意不需要对${\theta }_o$进行正则化，其用于偏差的计算。对应地，其梯度的计算公式如下：

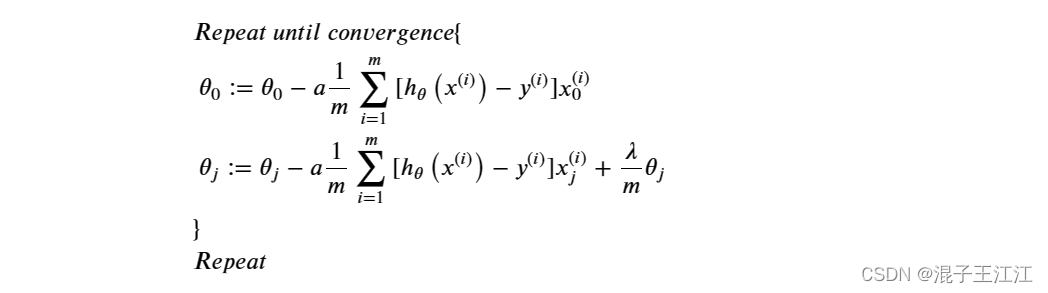
接下来，你需要编写代码实现正则化逻辑回归算法的代价函数和梯度的向量化实现。

###在这里填入代码###
def costReg(theta, X, y, learningRate):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
    second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))
    reg = (learningRate / (2 * len(X))) * np.sum(np.power(theta[:,1:theta.shape[1]], 2))
    return np.sum(first - second) / len(X) + reg

def gradientReg(theta, X, y, learningRate):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    
    parameters = int(theta.ravel().shape[1])
    error = sigmoid(X * theta.T) - y
    
    grad = ((X.T * error) / len(X)).T + ((learningRate / len(X)) * theta)
    
    # intercept gradient is not regularized
    grad[0, 0] = np.sum(np.multiply(error, X[:,0])) / len(X)
    
    return np.array(grad).ravel()

1.4 多分类-分类器

现在我们已经定义了代价函数和梯度函数，现在我们需要构建一个分类器。对于手写字识别，我们有10个可能的类（0-9），但逻辑回归是一个二分类问题。

在本练习中，你的任务是实现一对一全分类方法，其中具有$k$个不同类的标签就有$k$个分类器，每个分类器在“类别 $i$”和“不是 $i$”之间决定。我们将把分类器训练包含在一个函数中，该函数计算10个分类器中的每个分类器的最终权重，并将权重返回为$[k,n+1]$的数组，其中$n$是参数数量。

需要注意的是：

• 需要添加${\theta }_0$以计算截距项。
• 将$y$从类标签转换为每个分类器的二进制（要么是类i，要么不是类i）。
• 使用scipy库的优化类的minimize函数来最小化每个分类器的代价函数。
• 将寻找到的最优参数分配给参数数组，并返回形状为$[k,n+1]$的参数数组。

其中，实现向量化代码最重要的地方是要保证正确地写入所有的矩阵，保证其维度正确。

###在这里填入代码###
from scipy.optimize import minimize

def one_vs_all(X, y, num_labels, learning_rate):
    rows = X.shape[0]
    params = X.shape[1]
    
    # k个分类器的参数，形状为(k,n+1)
    all_theta = np.zeros((num_labels, params + 1))
    
    # 插入值为1的列，用于计算截距项
    X = np.insert(X, 0, values=np.ones(rows), axis=1)
    
    # 将分类标签转换为0-1标识
    for i in range(1, num_labels + 1):
        theta = np.zeros(params + 1)
        y_i = np.array([1 if label == i else 0 for label in y])
        y_i = np.reshape(y_i, (rows, 1))
        
        # 使用minimize函数最小化代价函数
        fmin = minimize(fun=costReg, x0=theta, args=(X, y_i, learning_rate), method='TNC', jac=gradientReg)
        all_theta[i-1,:] = fmin.x
    
    return all_theta

我们来检查下需要初始化的变量，以及变量的形状：

rows = data['X'].shape[0]
params = data['X'].shape[1]

all_theta = np.zeros((10, params + 1))

X = np.insert(data['X'], 0, values=np.ones(rows), axis=1)

theta = np.zeros(params + 1)

y_0 = np.array([1 if label == 0 else 0 for label in data['y']])
y_0 = np.reshape(y_0, (rows, 1))

X.shape, y_0.shape, theta.shape, all_theta.shape

((5000, 401), (5000, 1), (401,), (10, 401))

其中，$theta$是一维数组，因此当它被转换为计算梯度代码中的矩阵时，它变成了形状为$(1,401)$的矩阵。同时，我们需要检查$y$中的类标签。

np.unique(data['y'])#看下有几类标签

array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10], dtype=uint8)

接下来，为了确保训练函数正确运行，运行以下代码查看是否得到合理的输出。

###请运行并测试你的代码###
all_theta = one_vs_all(data['X'], data['y'], 10, 1)
all_theta

array([[-2.38222932e+00,  0.00000000e+00,  0.00000000e+00, ...,
         1.30374397e-03, -5.86808514e-10,  0.00000000e+00],
       [-3.18524878e+00,  0.00000000e+00,  0.00000000e+00, ...,
         4.45926913e-03, -5.08409291e-04,  0.00000000e+00],
       [-4.79666159e+00,  0.00000000e+00,  0.00000000e+00, ...,
        -2.87052349e-05, -2.47186328e-07,  0.00000000e+00],
       ...,
       [-7.98357621e+00,  0.00000000e+00,  0.00000000e+00, ...,
        -8.96090488e-05,  7.22728180e-06,  0.00000000e+00],
       [-4.57238599e+00,  0.00000000e+00,  0.00000000e+00, ...,
        -1.33747950e-03,  1.00013367e-04,  0.00000000e+00],
       [-5.40397976e+00,  0.00000000e+00,  0.00000000e+00, ...,
        -1.16560839e-04,  7.87437962e-06,  0.00000000e+00]])

1.5 使用分类器进行预测

我们现在准备好最后一步，你需要使用训练完毕的分类器预测每个图像的标签。

对于这一步，我们将计算每个类的类概率，对于每个训练样本（使用向量化代码），并将输出类标签为具有最高概率的类。

###在这里填入代码###
def predict_all(X, all_theta):
    rows = X.shape[0]
    params = X.shape[1]
    num_labels = all_theta.shape[0]
    
    # 与之前一样，需要插入一列确保矩阵形状
    X = np.insert(X, 0, values=np.ones(rows), axis=1)
    
    # 将其转换为矩阵
    X = np.matrix(X)
    all_theta = np.matrix(all_theta)
    
    # 计算每个训练样本所属每个类别的概率
    h = sigmoid(X * all_theta.T)
    
    # 创建具有最大概率的索引数组
    h_argmax = np.argmax(h, axis=1)
    
    # 因为我们的数组是零索引的，所以我们需要为真正的标签预测+1
    h_argmax = h_argmax + 1
    
    return h_argmax

现在我们可以使用predict_all函数为每个实例生成类预测，看看我们的分类器是如何工作的。

###请运行并测试你的代码###
y_pred = predict_all(data['X'], all_theta)
correct = [1 if a == b else 0 for (a, b) in zip(y_pred, data['y'])]
accuracy = (sum(map(int, correct)) / float(len(correct)))
print ('accuracy = {0}%'.format(accuracy * 100))

accuracy = 94.46%