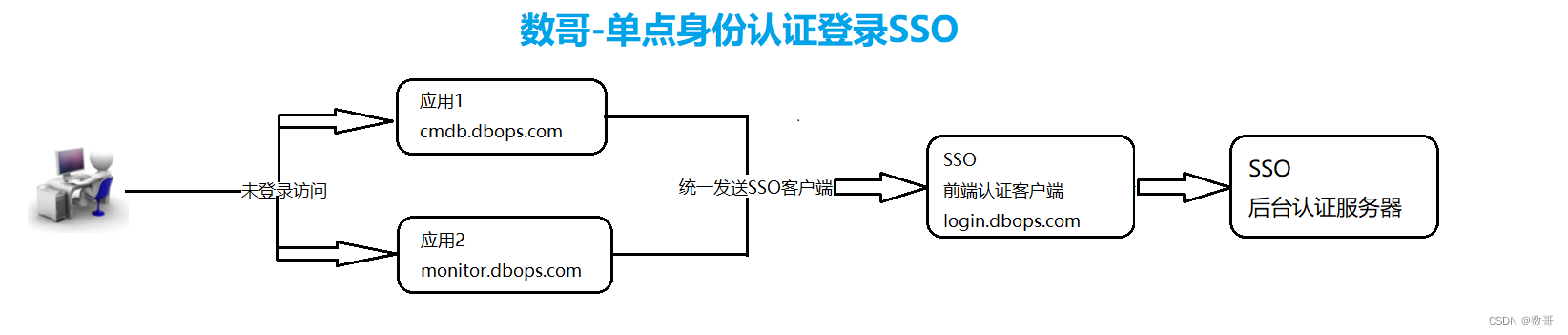
阵列信号处理笔记（1）

预备知识

  如图所示的球坐标系中，任意一阵元的位置可以用 $(r,\varphi ,\theta )$唯一表示，其直角系下的坐标$\mathbf{p}=(x,y,z{)}^T$的关系可以通过以下三个方程建立
$$\begin{array}{r}\{\begin{array}{rl}x& =r\sin \theta \cos \varphi \\ y& =r\sin \theta \sin \varphi \\ z& =r\cos \theta \end{array}\end{array}\text{\hspace{1em}(1)}$$

  实际上，一个阵列中往往包含若干个阵元，其位置按照某一特定规则布置，例如沿直线均匀排布的均匀线性阵（ULA），沿着球面排布的阵列，甚至以一种类似银河系星图案排布的多旋臂对数螺旋。无论是何种阵列，其对一特定外信号场$f_{src}(t)$的响应总能使用矢量$\mathbf{f}(t,\mathbf{p})$表示，也就是各阵元在空域上对外信号场的采样
$$\mathbf{f}(t,\mathbf{p})=\left(\begin{array}{c}f(t,{\mathbf{p}}_0)\\ f(t,{\mathbf{p}}_1)\\ ⋮\\ f(t,{\mathbf{p}}_{\mathbf{N}-1})\end{array}\right)\text{\hspace{1em}(2)}$$

从延时到阵列流形矢量

  假设外场信号$f_{src}(t)$为一平面波，即各阵元所接收的信号之间没有本质的不同，仅存在时延的差异，那么显然单个阵元的输出应该为$f_{src}(t)$与带有不同延时$\tau$的冲激信号相卷积。现在令
$$\mathbf{v}(t)=\left(\begin{array}{c}\delta (t-{\tau }_0)\\ \delta (t-{\tau }_1)\\ ⋮\\ \delta (t-{\tau }_{N-1})\end{array}\right)\text{\hspace{1em}(3)}$$
为了计算$\tau$的大小，现零波达矢量$\mathbf{a}$（波面的法向量，方向指向阵元）为
$$\mathbf{a}=\left(\begin{array}{c}{a}_x\\ a_y\\ a_z\end{array}\right)=-\left(\begin{array}{c}\sin \theta \cos \varphi \\ \sin \theta \sin \varphi \\ \cos \theta \end{array}\right)\text{\hspace{1em}(4)}$$
这里添加负号的原因是，我们要保证计算出来时延能正确反映阵元相对于位置情况，例如某一阵元A比阵元B晚接收到信号，那么B应该在A的后面而不是前面。根据幼儿园学习的“点与平面位置距离公式”，设某一时刻波面表达式为$a_{x}x+a_{y}y+a_{z}z+b=0$，那么坐标为${\mathbf{p}}_{\mathbf{n}}$的阵元与该时刻波面的距离$d$为
$$d_n=\frac{a_x{p}_{x_n}+a_y{p}_{y_n}+a_z{p}_{z_n}+b}{\sqrt{a_x^2+a_y^2+a_z^2}}={\mathbf{a}}^T{\mathbf{p}}_{\mathbf{n}}+b\text{\hspace{1em}(5)}$$
注意$|a|=1$。实际上我们只关心阵元之间相对距离而不是精确距离，因为波面是可以任取的，故忽略最后的$b$，从而
$${\tau }_n=\frac{{\mathbf{a}}^T{\mathbf{p}}_{\mathbf{n}}}{c}\text{\hspace{1em}(6)}$$
其中$c$为波在介质中的传播速度。现在定义一个新的量波数$\mathbf{k}$
$$\mathbf{k}=\frac{w}{c}\mathbf{a}=\frac{2\pi }{\lambda }\mathbf{a}\text{\hspace{1em}(7)}$$
其表示在一个波长范围内的角度变化率，也就相当于波的空域角频率。需要注意的是，这里波数是一个矢量而非标量，因为在波数中隐含了波的传播方向（波矢，因为空间是三维的），也就是波面的法线方向。波数是空域的角频率，这个概念可以类比时域角频率$w$和周期，如图所示。

  由于
$$\mathbf{f}(t)=\mathbf{v}(t)\ast f_{src}(t)\text{\hspace{1em}(8)}$$
（这里省去了变量$\mathbf{p}$，其实应该是$\mathbf{f}(t,\mathbf{p})$)对其两边同时做傅里叶变换可得
$$\mathbf{F}(w)=V(w){\mathbf{F}}_{src}(w)\text{\hspace{1em}(9)}$$
其中
$$\mathbf{V}(w)=\left(\begin{array}{c}{e}^{-jw{\tau }_0}\\ e^{-jw{\tau }_1}\\ ⋮\\ e^{-jw{\tau }_{N-1}}\end{array}\right)\text{\hspace{1em}(10)}$$
令波数为自变量，将$\mathbf{V}$的变量做个替换，记替换后为${\mathbf{v}}_{\mathbf{k}}(\mathbf{k})$，也就是
$$\mathbf{v}(\mathbf{k})=\left(\begin{array}{c}{e}^{-j{\mathbf{k}}^T{\mathbf{p}}_0}\\ e^{-j{\mathbf{k}}^T{\mathbf{p}}_1}\\ ⋮\\ e^{-j{\mathbf{k}}^T{\mathbf{p}}_{N-1}}\end{array}\right)\text{\hspace{1em}(11)}$$
称${\mathbf{v}}_{\mathbf{k}}(\mathbf{k})$为阵列流形，其中下标$\mathbf{k}$代表所定义的阵列流形参数属于$\mathbf{k}$域（波数域）。

频率波数响应

  如果将每一个阵元之前插入一个线性时不变系统用于对阵元接收信号进行独立的处理，再将其输出累加，即
$$y(t)=\sum _{n=0}^{N-1}{\int }_{-\infty }^{\infty }{f}_n(t,{\mathbf{p}}_{\mathbf{n}})h_n(t-\tau )\mathrm{d}\tau \text{\hspace{1em}(12)}$$

  实际上，若交换求和与积分次序，不难发现
$$y(t)={\int }_{-\infty }^{\infty }\mathbf{h}(t-\tau {)}^T\mathbf{f}(t,{\mathbf{p}}_n)\mathrm{d}\tau \text{\hspace{1em}(13)}$$

  对两边同时做傅里叶变换可得
$$Y(w)=\mathbf{H}(w{)}^T\mathbf{F}(w)=\mathbf{H}(w{)}^T{\mathbf{v}}_{\mathbf{k}}(\mathbf{k}){\mathbf{F}}_{src}(w)\text{\hspace{1em}(14)}$$

  令
$$\gamma (w,\mathbf{k})=\mathbf{H}(w{)}^T{\mathbf{v}}_{\mathbf{k}}(\mathbf{k})$$
  称$\gamma (w,\mathbf{k})$为阵列的频率-波数响应。

   2023年06月04日 于绍兴