1.证明熵的可加性

2.假设一帧视频图像可以认为是由3*10的五次方个像素组成(每像素均独立变化),如果每个像素可取128个不同的等概率亮度表示。请计算出每帧图像含多少信息量?若有一口述者在约12000个汉字的字汇中选400个字来口述此电视图像,试问口述者描述此图像所需要的信息量是多少(假设汉字是等概率独立分布)?若要恰当地描述此图像,口述者在口述中至少需要用多少汉字?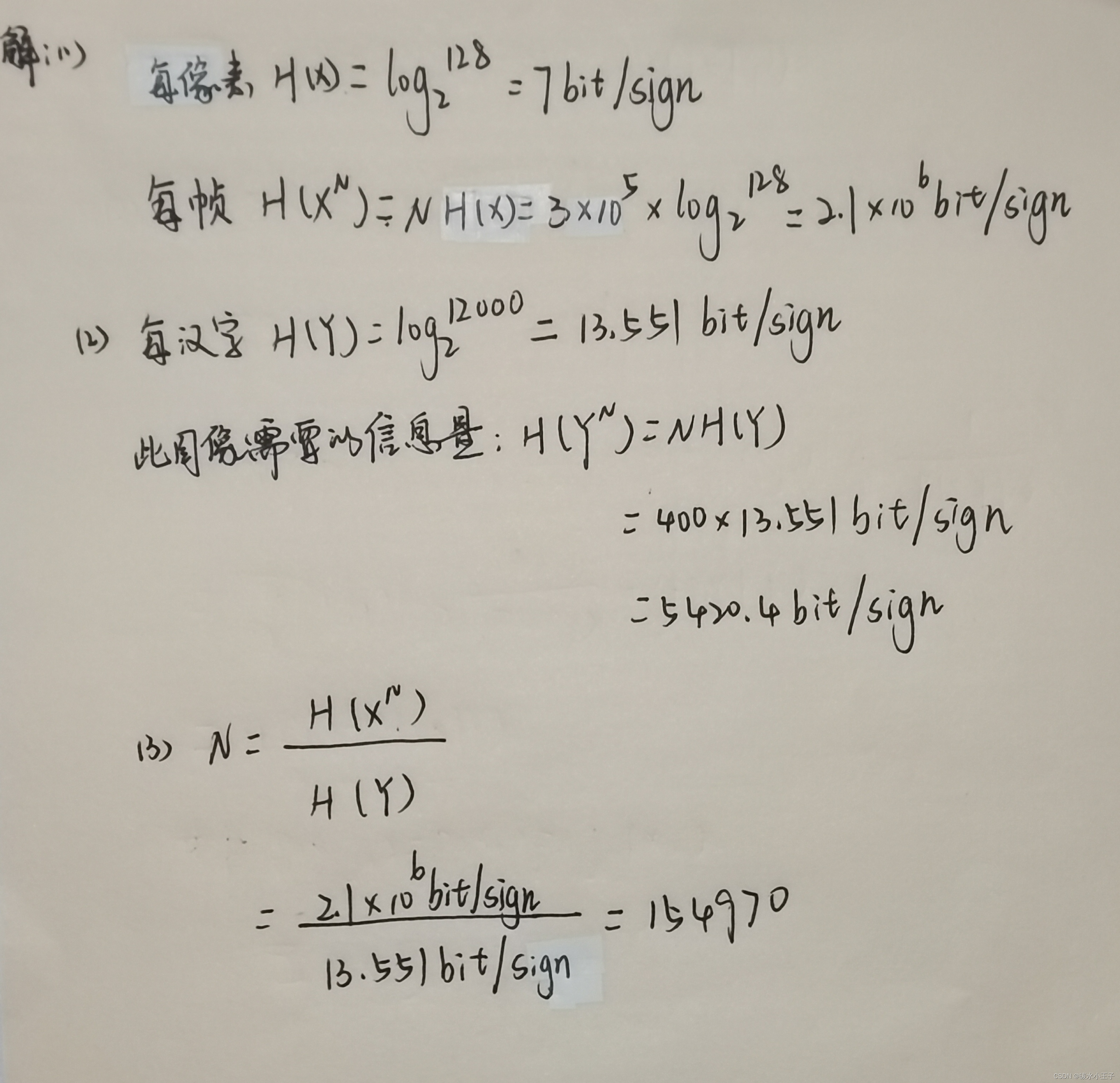
3.信源:产生要传输的消息。
4.信源编码:对信源输出进行变化(消除冗余,压缩),提高信息传输的有效性。
5.信道编码:对信源编码输出变换(加入冗余),提高抗干扰能力,提高信息传输的可靠性。
6.加密编码:提高传输的安全性。
7.信道:信号传输的介质。
8.信宿:接受信源传输的消息。
9.无失真信源编码定理(香农第一定理)
如果信源编码码率 R (编码后传送信源符号所需比特数)不小于信源的熵 H ( X ),就存在无失真编码,反之不存在无失真编码。
10.有噪信道编码定理(香农第二定理)
如果信息传输速率小于信道容量,则总可以找到一种编码方式使得当编码序列足够长时传输差错任意小。反之不存在使差错任意小的编码。
11.限失真信源编码定理(香农第三定理)
只要码字足够长,总可以找到一种编码,使得当编码码率 R > R ( D )时,码的平均失真 D ;反之不存在平均失真 D 的编码。在允许一定失真度 D 的情况下,信源输出的信息率可以压缩到 R ( D )。
R ( D )称为信息率失真函数,是满足失真准则(平均失真 D )下,每个信源符号所需最小编码比特数。
12.平均错误概率不仅与信道本身的统计特性有关,还与编码方法和译码准则有关。
13.事件发生的概率越小,不确定性就越大。概率等于1的必然事件,不存在不确定性。
14.如果知道事件 Xi 已发生,则事件包含的自信息定义为:
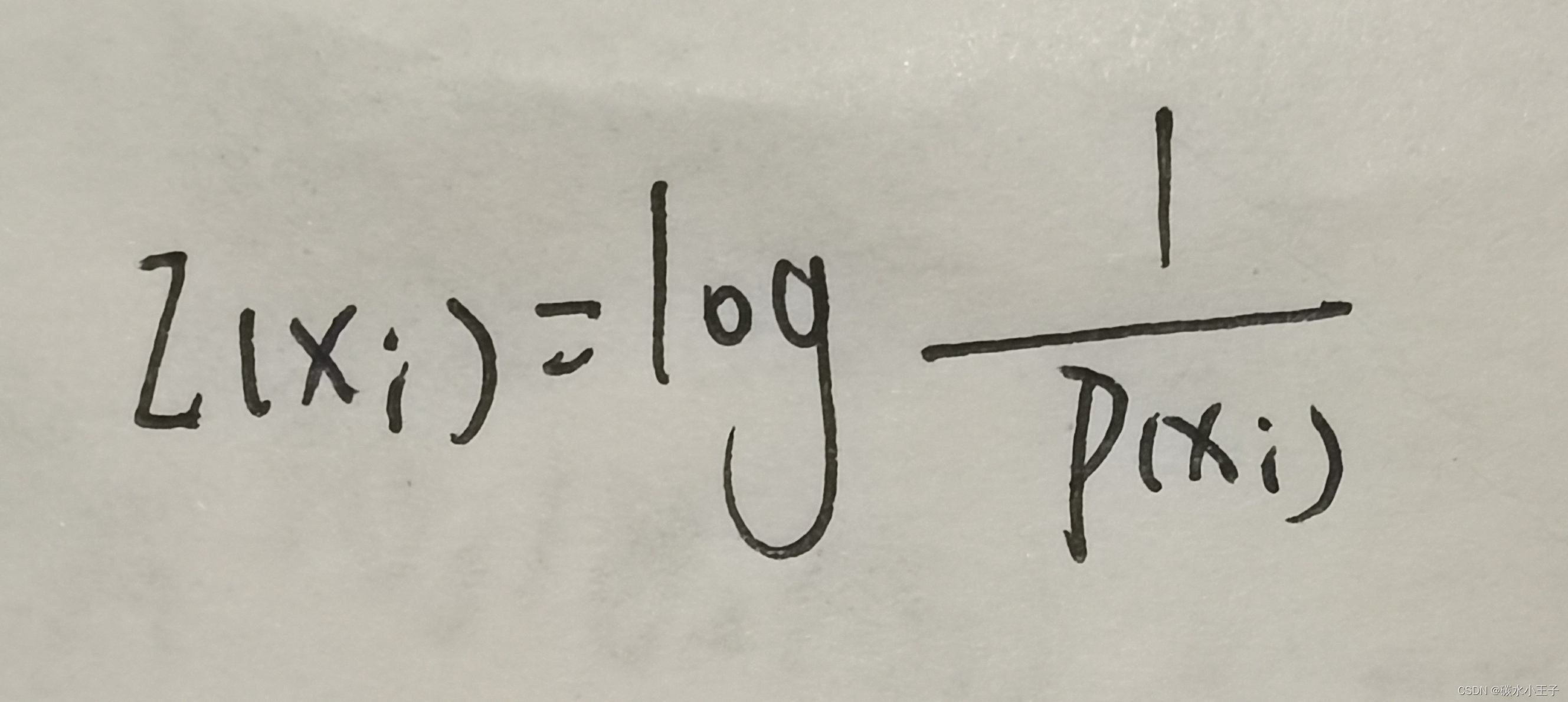
15.自信息的含义
当事件 Xi 发生以前表示事件 Xi 发生的不确定性;
当事件 Xi 发生以后表示事件 X 所包含的信息量。
16.信源自信息量为非负值;当事件发生概率为1时,自信息量为0;当事件发生概率为0时,自信息量为无穷大;自信息量是事件发生概率的单调递减函数。
5.联合自信息量
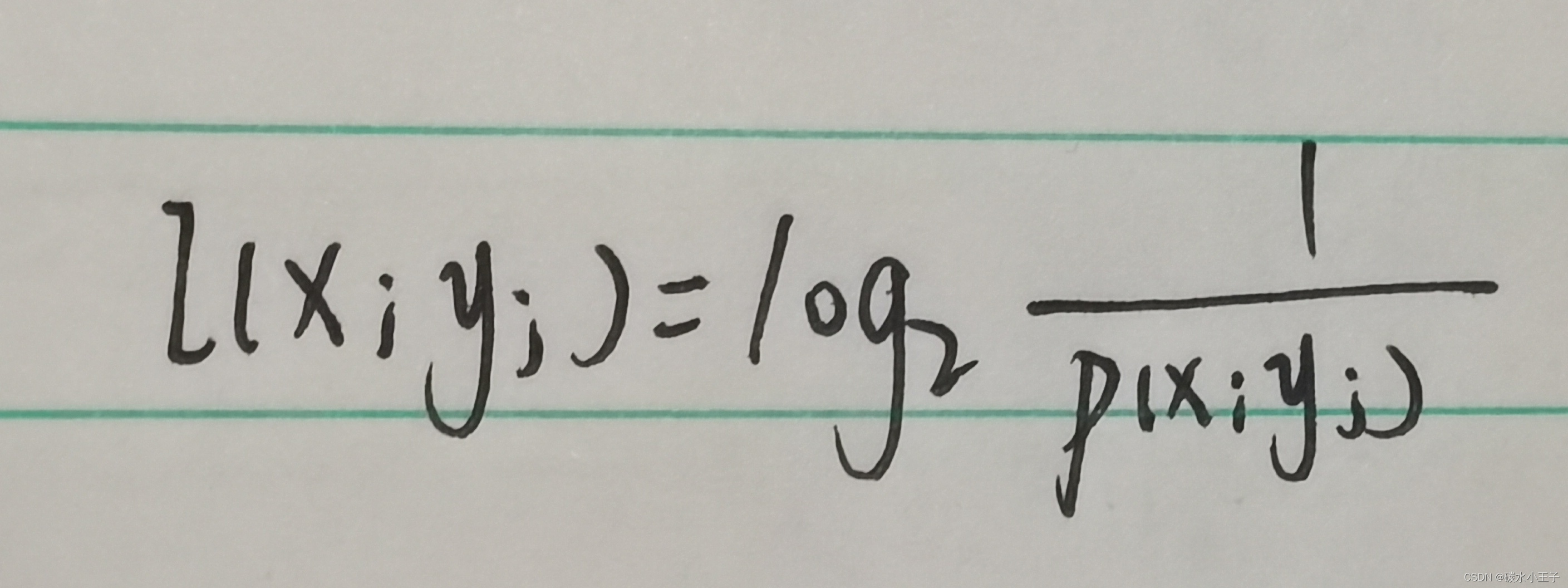 当 X 和 Y 相互独立时:
当 X 和 Y 相互独立时:
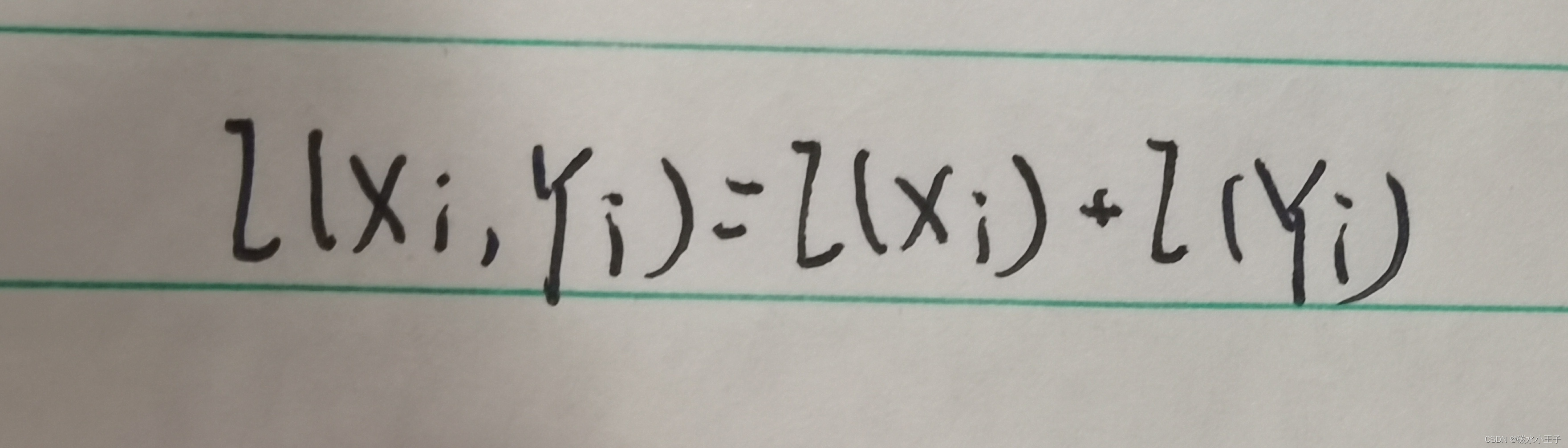
6.关于信道容量与信息的可靠传输
有噪信道编码定理(香农第二定理)是信道编码的理论基础,其内容是:如果信息传输速率小于信道容量,则总可找到一种编码方式使得当编码序列足够长时传输差错任意小,反之不存在使差错任意小的编码。
7.信息率失真理论(数据压缩的理论基础)
限失真信源编码定理(香农第三定理)的是有损压缩编码的理论基础,其内容是:只要码字足够长,总可找到一种编码,使得当信源编码的码率> R ( D )时,码的平均失真 D ;反之,如果信源编码的码率< R ( D ),就不存在平均失真 D 的编码。可以简述为:在允许一定失真度 D 的情况下,信源输出的信息率可压缩到 R ( D )
R ( D )称为信息率失真函数,是满足失真准则(平均失真 D )下,每信源符号所需最小编码比特数。
8.
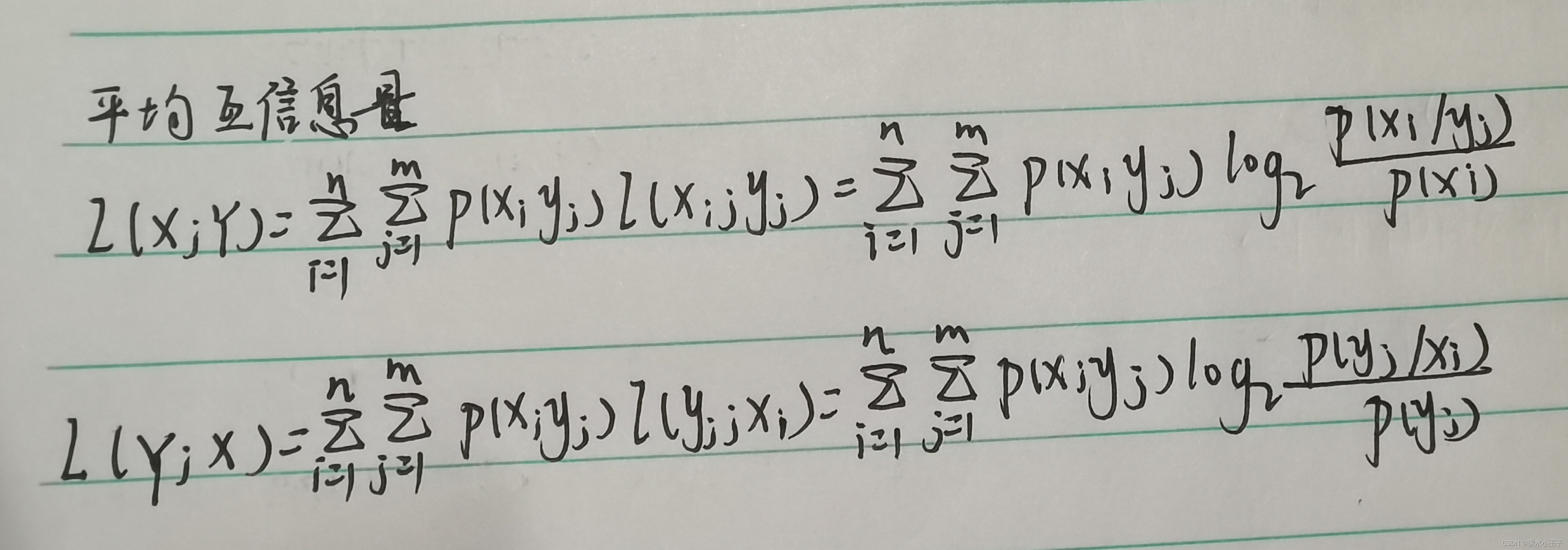
9.熵的基本性质和定理