图像增强:主要是一种 主观处理,而图像复原很大程度上是一种 客观处理。
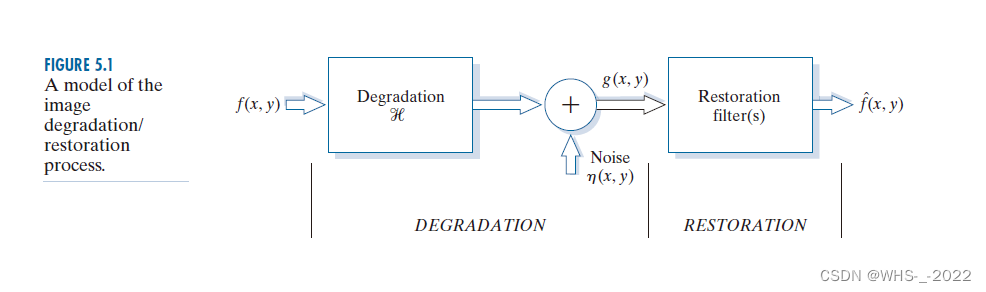
5.1 图像退化/复原处理的一个模型
如图5.1 本章把图像退化建模为一个算子 H \mathcal{H} H 该算子 与一个加性噪声项 η ( x , y ) η(x,y) η(x,y) 共同对输入图像 f ( x , y ) f(x,y) f(x,y) 进行运算,生成一幅退化图像 g ( x , y ) g(x,y) g(x,y)。
如果
H
\mathcal{H}
H 是一个线性位置不变算子,那么空间域中的退化图像为:
g ( x , y ) = h ( x , y ) ⋆ f ( x , y ) + η ( x , y ) (5.1) g(x, y)=h(x, y) \star f(x, y)+\eta(x, y)\tag{5.1} g(x,y)=h(x,y)⋆f(x,y)+η(x,y)(5.1)
由空间域卷积定理可知,式(5.1)在频率域中的等效公式为:
G
(
u
,
v
)
=
H
(
u
,
v
)
F
(
u
,
v
)
+
N
(
u
,
v
)
G(u, v)=H(u, v) F(u, v)+N(u, v)
G(u,v)=H(u,v)F(u,v)+N(u,v)
5.2 噪声模型
5.2.1 噪声的空间和频率特性
当噪声的傅里叶谱是常量时,这类噪声通常称为白噪声。
除了空间周期噪声(5.2.3节, 教材P225)之外,本章假设噪声与空间坐标无关,并且与图像本身也不相关。
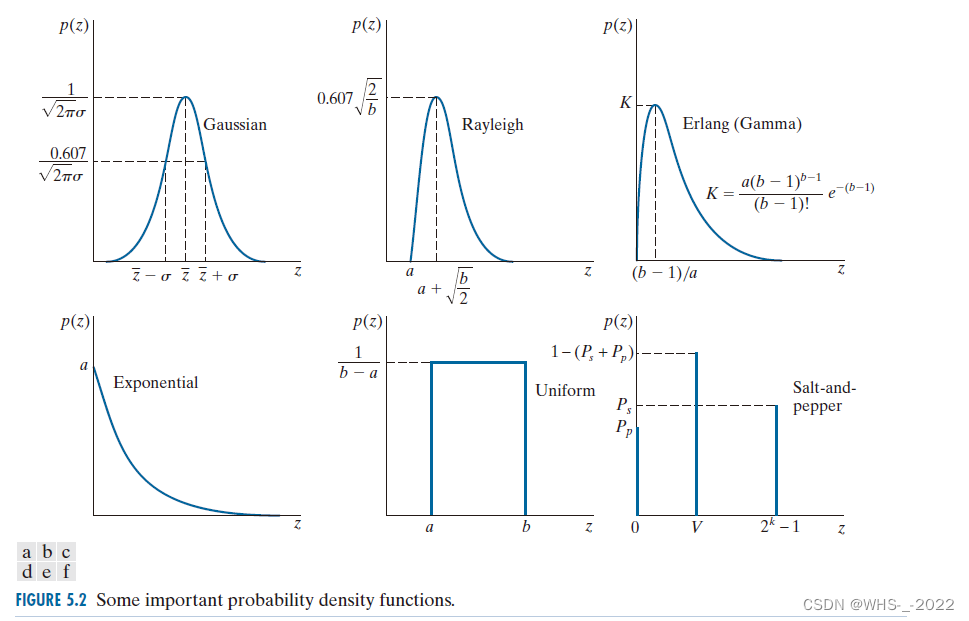
5.2.2 6种重要的噪声概率密度函数
5.3 只存在噪声的复原——空间滤波
5.3.1 均值滤波器
- 算术平均滤波器(最简单的均值滤波器)
f ^ ( x , y ) = 1 m n ∑ ( r , c ) ∈ S x y g ( r , c ) \hat{f}(x, y)=\frac{1}{m n} \sum_{(r, c) \in S_{x y}} g(r, c) f^(x,y)=mn1(r,c)∈Sxy∑g(r,c)
均值滤波平滑图像中的局部变化,会降低图像噪声,但会模糊图像。
- 几何均值滤波器
f ^ ( x , y ) = [ ∏ ( r , c ) ∈ S x y g ( r , c ) ] 1 m n \hat{f}(x, y)=\left[\prod_{(r, c) \in S_{x y}} g(r, c)\right]^{\frac{1}{m n}} f^(x,y)= (r,c)∈Sxy∏g(r,c) mn1
几何均值滤波器实现的平滑可与算术平均滤波器相比,但损失的图像细节更少。“几何”二字来源于圆上的弦长。几何均值会略微惩罚偏离均值的成分。
- 谐波平均滤波器
f ^ ( x , y ) = m n ∑ ( r , c ) ∈ S x y 1 g ( r , c ) \hat{f}(x, y)=\frac{m n}{\sum_{(r, c) \in S_{x y}} \frac{1}{g(r, c)}} f^(x,y)=∑(r,c)∈Sxyg(r,c)1mn
能处理类似于高斯噪声的其他噪声、盐粒噪声(√),但不能处理胡椒噪声(×)。因为调和平均数会剧烈的惩罚偏离平均值的较低值,会导致图片整体偏暗。(调和均值)
- 反谐波平均滤波器
f ^ ( x , y ) = ∑ ( r , c ) ∈ S x y g ( r , c ) Q + 1 ∑ ( r , c ) ∈ S x y g ( r , c ) Q \hat{f}(x, y)=\frac{\sum_{(r, c) \in S_{x y}} g(r, c)^{Q+1}}{\sum_{(r, c) \in S_{x y}} g(r, c)^{Q}} f^(x,y)=∑(r,c)∈Sxyg(r,c)Q∑(r,c)∈Sxyg(r,c)Q+1
其中, Q Q Q 称为滤波器的阶数。适用于降低或消除椒盐噪声。如果 Q Q Q 的符号选择错误 会引起灾难性的后果。
5.3.2 统计排序滤波器
- 中值滤波器(最著名的统计排序滤波器)
f ^ ( x , y ) = median ( r , c ) ∈ S x y { g ( r , c ) } \hat{f}(x, y)=\operatorname{median}_{(r, c) \in S_{x y}}\{g(r, c)\} f^(x,y)=median(r,c)∈Sxy{g(r,c)}
与相同尺寸的线性平滑滤波器相比,中值滤波器能有效降低某些随机噪声,且模糊度要小得多。对于单极和双极冲激噪声,中值滤波器效果更好。
- 最大值和最小值滤波器
分别是为了降低胡椒噪声和盐粒噪声。
- 中点滤波器
f ^ ( x , y ) = 1 2 [ max ( r , c ) ∈ S x y { g ( r , c ) } + min ( r , c ) ∈ S x y { g ( r , c ) } ] \hat{f}(x, y)=\frac{1}{2}\left[\max _{(r, c) \in S_{x y}}\{g(r, c)\}+\min _{(r, c) \in S_{x y}}\{g(r, c)\}\right] f^(x,y)=21[(r,c)∈Sxymax{g(r,c)}+(r,c)∈Sxymin{g(r,c)}]
计算滤波器包围区域中最大值和最小值之间的中点。
- 修正阿尔法均值滤波器
f ^ ( x , y ) = 1 m n − d ∑ ( r , c ) ∈ S x y g R ( r , c ) , 0 ≤ d ≤ m n − 1 \hat{f}(x, y)=\frac{1}{m n-d} \sum_{(r, c) \in S_{x y}} g_{R}(r, c), \quad 0 \leq d \leq m n-1 f^(x,y)=mn−d1(r,c)∈Sxy∑gR(r,c),0≤d≤mn−1
适用于处理多种混合噪声。
5.5 线性位置不变退化
一个算子对于任意 f ( x , y ) f(x,y) f(x,y)、 α \alpha α、 β \beta β,如果
H [ f ( x − α , y − β ) ] = g ( x − α , y − β ) \mathcal{H}[f(x-\alpha, y-\beta)]=g(x-\alpha, y-\beta) H[f(x−α,y−β)]=g(x−α,y−β)
则称具有输入/输出关系为线性位置不变退化,该定义说明:图像中任意一点处的响应只取决于该点处的输入值,而与该点的位置无关。
5.6 估计退化函数
观察法、试验法、建模法
5.7 逆滤波
原图像傅里叶变换的一个估计:
F ^ ( u , v ) = F ( u , v ) + N ( u , v ) H ( u , v ) \hat{F}(u, v)=F(u, v)+\frac{N(u, v)}{H(u, v)} F^(u,v)=F(u,v)+H(u,v)N(u,v)
即使知道退化函数 H ( u , v ) H(u, v) H(u,v),也不能准确复原未退化的图像,因为 N ( u , v ) N(u, v) N(u,v) 未知。如果退化函数 H ( u , v ) H(u, v) H(u,v) 是零或是非常小的值,则 N ( u , v ) / H ( u , v ) N(u,v)/H(u, v) N(u,v)/H(u,v) 很容易支配 F ( u , v ) F(u, v) F(u,v) 项。
5.8 最小均方误差(维纳)滤波
F ^ ( u , v ) = [ H ∗ ( u , v ) S f ( u , v ) S f ( u , v ) ∣ H ( u , v ) ∣ 2 + S η ( u , v ) ] G ( u , v ) = [ H ∗ ( u , v ) ∣ H ( u , v ) ∣ 2 + S η ( u , v ) / S f ( u , v ) ] G ( u , v ) = [ 1 H ( u , v ) ∣ H ( u , v ) ∣ 2 ∣ H ( u , v ) ∣ 2 + S η ( u , v ) / S f ( u , v ) ] G ( u , v ) \begin{aligned} \hat{F}(u, v) & =\left[\frac{H^{*}(u, v) S_{f}(u, v)}{S_{f}(u, v)|H(u, v)|^{2}+S_{\eta}(u, v)}\right] G(u, v)=\left[\frac{H^{*}(u, v)}{|H(u, v)|^{2}+S_{\eta}(u, v) / S_{f}(u, v)}\right] G(u, v) \\ & =\left[\frac{1}{H(u, v)} \frac{|H(u, v)|^{2}}{|H(u, v)|^{2}+S_{\eta}(u, v) / S_{f}(u, v)}\right] G(u, v) \end{aligned} F^(u,v)=[Sf(u,v)∣H(u,v)∣2+Sη(u,v)H∗(u,v)Sf(u,v)]G(u,v)=[∣H(u,v)∣2+Sη(u,v)/Sf(u,v)H∗(u,v)]G(u,v)=[H(u,v)1∣H(u,v)∣2+Sη(u,v)/Sf(u,v)∣H(u,v)∣2]G(u,v)
若噪声为零则噪声功率谱消失 维纳滤波器简化为 逆滤波器。
5.9 约束最小二乘方滤波
5.10 几何均值滤波
5.11 评价复原图像质量的测度
空间域信噪比:
S N R = ∑ x = 0 M − 1 ∑ y = 0 N − 1 [ f ^ ( x , y ) ] 2 / ∑ x = 0 M − 1 ∑ y = 0 N − 1 [ f ( x , y ) − f ^ ( x , y ) ] 2 \mathrm{SNR}=\sum_{x=0}^{M-1} \sum_{y=0}^{N-1}[\hat{f}(x, y)]^{2} / \sum_{x=0}^{M-1} \sum_{y=0}^{N-1}[f(x, y)-\hat{f}(x, y)]^{2} SNR=x=0∑M−1y=0∑N−1[f^(x,y)]2/x=0∑M−1y=0∑N−1[f(x,y)−f^(x,y)]2
频率域信噪比:
S
N
R
=
∑
u
=
0
M
−
1
∑
v
=
0
N
−
1
∣
F
(
u
,
v
)
∣
2
/
∑
u
=
0
M
−
1
∑
v
=
0
N
−
1
∣
N
(
u
,
v
)
∣
2
\mathrm{SNR}=\sum_{u=0}^{M-1} \sum_{v=0}^{N-1}|F(u, v)|^{2} / \sum_{u=0}^{M-1} \sum_{v=0}^{N-1}|N(u, v)|^{2}
SNR=u=0∑M−1v=0∑N−1∣F(u,v)∣2/u=0∑M−1v=0∑N−1∣N(u,v)∣2
均方误差:
M
S
E
=
1
M
N
∑
x
=
0
M
−
1
∑
y
=
0
N
−
1
[
f
(
x
,
y
)
−
f
^
(
x
,
y
)
]
2
\mathrm{MSE}=\frac{1}{M N} \sum_{x=0}^{M-1} \sum_{y=0}^{N-1}[f(x, y)-\hat{f}(x, y)]^{2}
MSE=MN1x=0∑M−1y=0∑N−1[f(x,y)−f^(x,y)]2