1 常微分方程（ODE）介绍

1.1 微分方程介绍和分类

举例：假设跳伞人的下落速度v于时间有如下关系：

$\frac{dv}{dt} = g-\frac{c}{m}v$ (1.1)

其中g为重力常数，m为质量，c为阻力系数。

被微分的量v因变量，与v有关的变量t称为自变量。
如果函数只有一个自变量，那么方程就称为常微分方程（ordinary differential equation，ODE）。
如果函数含有两个或者多个自变量，则成为偏微分方程（partialdifferential equation，PDE）。

此外，微分方程也可以根据阶数来分类：最高阶导数是一阶导数，则称为一阶微分方程（first-order-equation）；最高阶导数是二阶导数，则称为二阶微分方程（second-order-equation）。例如如（1.1）中就是一阶微分方程，下式（1.2）就是一个二阶微分方程。

$m\frac{d^2x}{dt^2} +c\frac{dx}{dt} + kx = 0$ (1.2)

高阶微分方程能简化成一阶方程组。考虑上式（1.2），定义新变量y，令
$y=\frac{dx}{dt}$ (1.3)

对上式取微分得：
$\frac{dy}{dt}=\frac{d^2x}{dt^2}$ (1.4)

将式（1.3）和（1.4）代入式（1.2）中得到：
$m\frac{dy}{dt} +cy + kx = 0$ (1.5)

于是原来的二阶微分方程（1.2）可等价于两个一阶方程组（1.3）和（1.5）。

同样的，其他的n阶微分方程也可以用类似的方式简化。

1.2 常微分方程得计算方法

非计算机计算方法：
常微分方程通常采用解析积分得方法来求解。如对于式(1.1)，先乘以dt，在进行积分得到：
$\int{(g-\frac{c}{m}v)dt}$ (1.6)

对于上式（1.6），是可以精确的推导出该积分得函数表达式的。因为该方程是线性的。

但在实际中，很多方程（是非线性的）精确解是无法求出的。于是提出了一个方法，就是将方程线性化。
（ $n$ 阶）线性常微分方程的一般形式是：
$a_n(x)y^{(n)}+...+a_2(x)y^{(2)}+a_1(x)y'++a_0(x)y = f(x)$ (1.7)
其中， $y^{(n)}$ 是y关于x的n阶导数， $a_n(x)$ 和 $f (x)$ 都是关于x的函数。因为该方程中未出现因变量y与其导数的乘积，也没有出现非线性函数。所以认为它是线性的。

如下式（1.8）是一个非线性微分方程：
$\frac{d^2x}{dt^2} +\frac{g}{l} sin(x)= 0$ (1.8)
由于含有 $s in (x)$ 为非线性函数，故该微分方程是非线性的。

线性常微分方程是可以通过解析法求解的。但是，大部分非线性方程无法精确求解。

1.3 线性微分方程求解的推导过程

拿一个简单的方程举例。首先给定函数：
$y=-0.5x^4+4x^3-10x^2+8.5x+1$ （1.9）
这是一个四次多项式。对其进行微分，就得到一个常微分方程：
$\frac{dy}{dx}=-2x^3+12x^2-20x+8.5$ （1.10）

对式（1.10）乘以dx，在进行积分得到：
$y=\int{(-2x^3+12x^2-20x+8.5)}dx$ （1.11）
应用积分法则得出解为：
$y=-0.5x^4+4x^3-10x^2+8.5x+C$ （1.12）
除了相差一个C外，其余都与原函数相同。这个C称为积分常数（constant of integration）。
出现一个任意常数C表明，积分的结果并不算是唯一的。无限多个常数C对应无限多个可能的函数，都满足微分方程。下图给出了6个满足条件的函数：
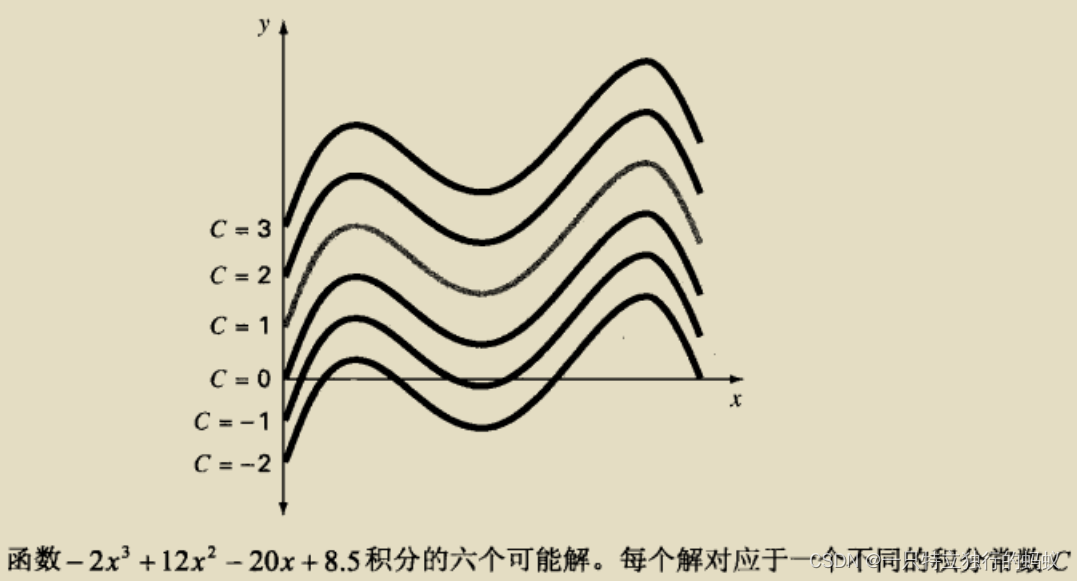
在这里插入图片描述

为了将解完全确定下来，微分方程通常伴随有辅助条件（auxiliary conditions）。对于一阶常微分方程，有一类被称为**初值（initial value）**的辅助条件，这类条件用于确定常数值，从而使得解是唯一的。例如，给式（1.11）添加初始条件x=0，y=1。带入式（1.12）中，可推导出C=1。于是就得到了唯一解：
$y=-0.5x^4+4x^3-10x^2+8.5x+1$
这个解同时满足常微分方程和指定的初始条件。