1、聚类
聚类与分类不同,聚类分析分通过分析大量含有一定规律但杂乱数据,得到数据间内在的逻辑,将杂乱的数据按照所得的数据规律划分成不同的种类。K-measn、DBSCAN和层次是当前广泛使用的三种聚类方法。以下对三种方法进行分析,选择适合的聚类方法。
| 方法 | K-means | 凝层次 | DBSCAN |
| 类型 | 基于原型的、划分的、完全的 | 层次的、完全的 | 基于密度的、划分的、部分的 |
| 基本原理 | 以样本非中心点到其所属的中心点的距离的平方和最小为目标来划分相应的类,并不断更新质心的位置和划分新类直至质心稳定 | 以每个点作为一个类为始,依据某种距离逐步合并“最接近”的类,直至所有的类被合并,形成有层次的聚类树 | 通过半径和邻域内样本点数量对密度进行定义,将核心点与其邻域内的所有核心点同处一类,将边界点归到邻域内核心点的类中 |
| 优点 | 1、收敛速度快: 2、算法可解释性好,原理简单; 3、调参(K)简单 | 可发现聚类间的层次关系 | 1、抗噪音; 2、能处理任意形状类;自动确定类数; |
| 缺点 | 1、易受初始值限制; 2、需首先确定K值 | 计算复杂度高; | 对半径和邻域内包含点数敏感 |
不同的方法特点不同,本次主要分析Kmeans聚类。
2、K-means聚类步骤
K-means算法主要有四个核心要点:
(1)簇个数k的选择
(2)各个样本点到“簇中心”的距离
(3)更新“簇中心”
(4)重复上述2、3过程,直至"簇中心"没有移动
基于上述四个核心要点,K-means算法具体步骤为:
(1)K值的选择:选取K个簇类的质心(通常为随机);
(2)距离度量:需要计算各个样本点到“簇中心”的距离,距离算法各有优劣,根据具体使用目标的不同采用合适的度量方法,常用且可靠的的度量方法有:
欧式距离:

曼哈顿距离:
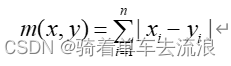
余弦相似度:
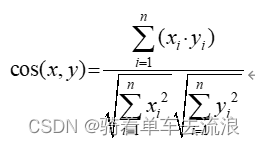
(3)新质心计算:根据第一计算距离的结果,更新“簇中心”,再计算各样本到“簇中心”的距离,与第二步类似。
(4)停止条件:每一次计算后,需要判断停止条件,达到条件时,满足需求,停止迭代计算。常用的停止要求有:
1)当质心不再改变,或给定loop最大次数loopLimit
2)当每个簇的质心,不再改变时就可以停止K-means
3)当loop次数超过looLimit时,停止K-means
4)只需要满足两者的其中一个条件,就可以停止K-means
5)如果Step4没有结束K-means,就再执行step2-step3-step4
6)如果Step4结束了K-means,则就打印(或绘制)簇以及质心
3、K-means算法评价指标
K-means算法的主要评价指标如下表所示:
| 指标 | 特点 |
| 紧密度(Compactness) | 紧密度代表每一个类别元素到该类中心的聚类,因此聚类算法的效果好,类中的各个元素到该类的距离越小,紧密度越小。 |
| 分割度(Seperation) | 分割度(Seperation)代表平均距离,计算式与上一节的距离方式一致,一般来说,不同类别的距离越远,分割度就越大,相应的不同类别之间的关系越弱,聚类效果越好。 |
| 误差平方和(SSE:) | 误差平方和代表聚类的目标,原则上聚类效果越好时,SSE越小。 |
| 轮廓系数(SilhouetteCoefficient) | 一个类别元素之间的距离应该越小越好,不同类别之间的元素则应该聚类越大,轮廓系数可以衡量整一个聚类的效果,当聚类效果好时,轮廓系数取得最大值+1,相反,聚类效果不好时,轮廓系数取得最小值-1。 |
4、K-means的实现过程
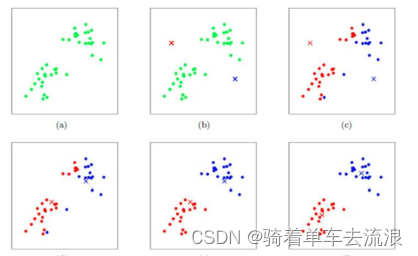
如图,K-means是先选定两个质心,求解其他点到两个质心的距离,进行第一次聚类,然后再在两类中选出新的质心,继续分类,不断迭代。